[자료구조] 그래프 - 3(그래프의 탐색)

그래프 또한 탐색을 해야한다!
그래프의 탐색과정은 어떻게 진행될까?
모든 정점을 돌아다니려면 어떻게 해야할까?

그래프의 탐색에는 별도의 정점을 모두 돌아다니기 위한 별도의 알고리즘 두 가지가 있다.

• 깊이 우선 탐색(Depth Frist Search : DFS)
• 너비 우선 탐색(Breadth First Search : BFS)

이를 살펴보자!

깊이 우선 탐색(Depth Frist Search : DFS)

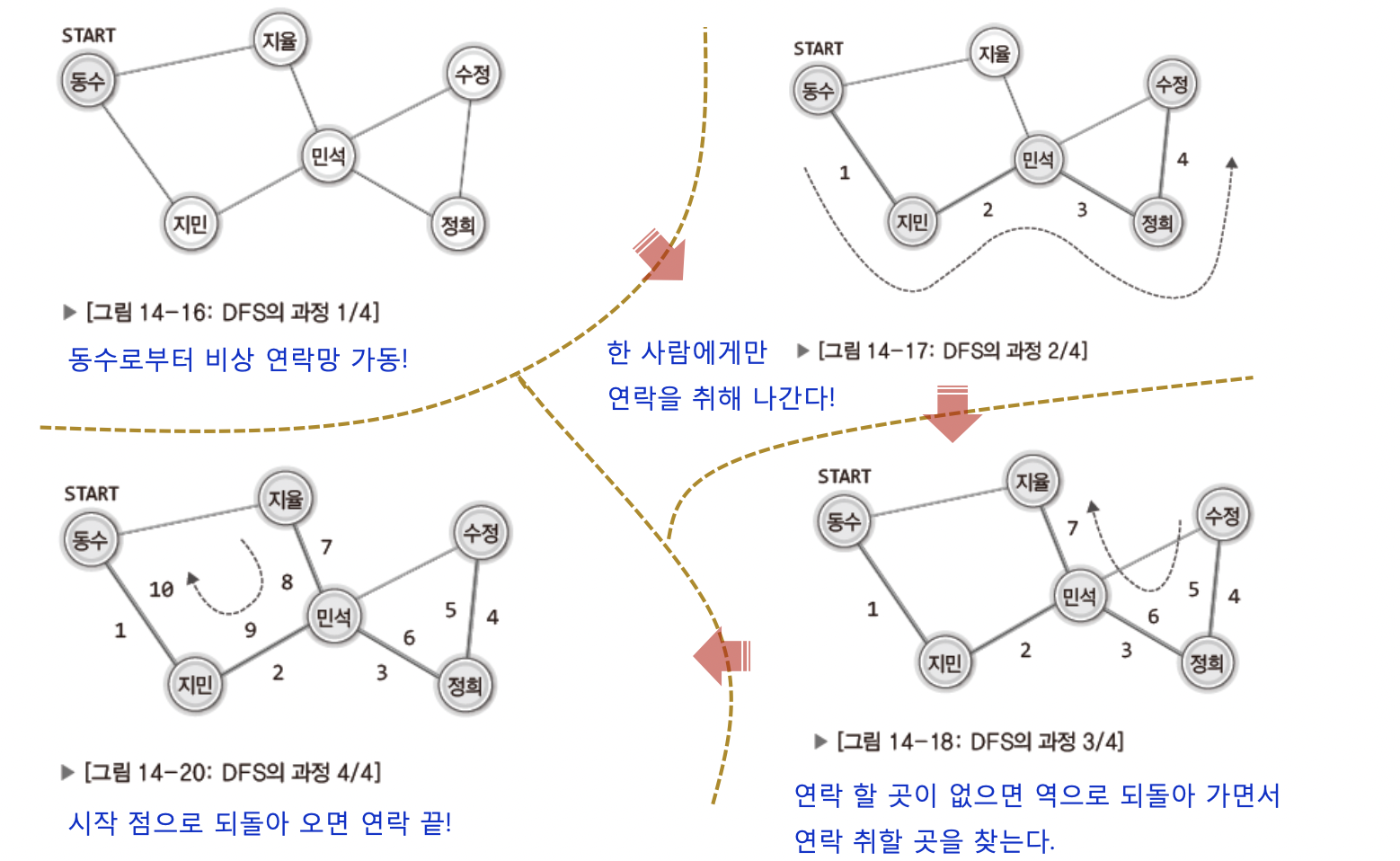
즉, 깊이 우선 탐색은 한 사람에게만 연락하고, 더 이상 연락할 사람이 없다면 나에게 연락 했던 사람에게
"야~ 나랑 연결된 애들은 연락 다 받았거든? 이제 너랑 연결된 애들 중에서 연락 안된 애 한테 연락해봐~"
라고 전달한다.

그렇게 모든 정점을 돌고 난 후, 역으로 돌아가면서 다시 동수에게 다시 연락이 가야 모든 사람이 연락을 받았다고 확신할 수 있다!!

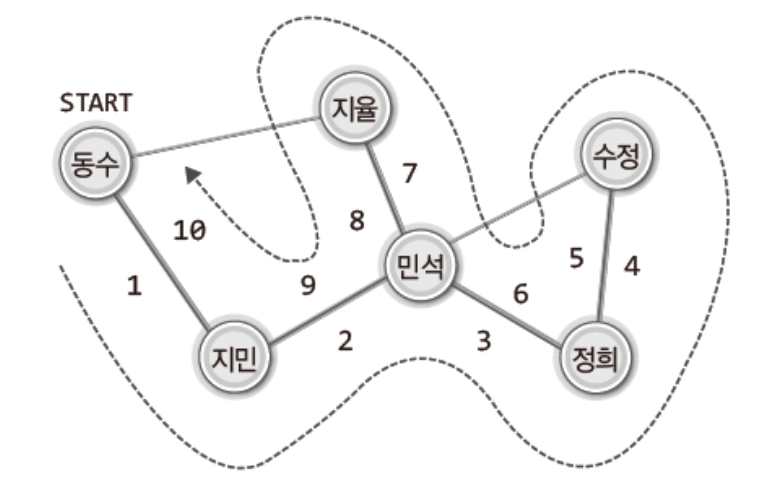
이를 한 그림에 나타내면 이렇다.

즉 DFS핵심 세 가지를 비상연락망에 빗대어 정리하면 다음과 같다.

• 한 사람에게만 연락을 한다.
• 연락할 사람이 없으면, 자신에게 연락한 사람에게 이를 알린다.
• 처음 연락을 시작한 사람의 위치에서 연락은 끝이 난다.

이게 DFS의 끝이다!
어떤가 간단하지 않는가!
그리고 어느정도 눈치가 있다면 역으로 돌아간다에서 어..?
역으로 돌아간다..? 스택!?!?!? 이 생각 날 수도 있다 ! !
이건 추후에 맞는지 확인하자.

너비 우선 탐색(Breadth First Search : BFS)

BFS 는 DFS 와 반대로
한 사람이 연락가능한 모든~ ! 사람에게 연락을 한다.
그럼 그림을 보자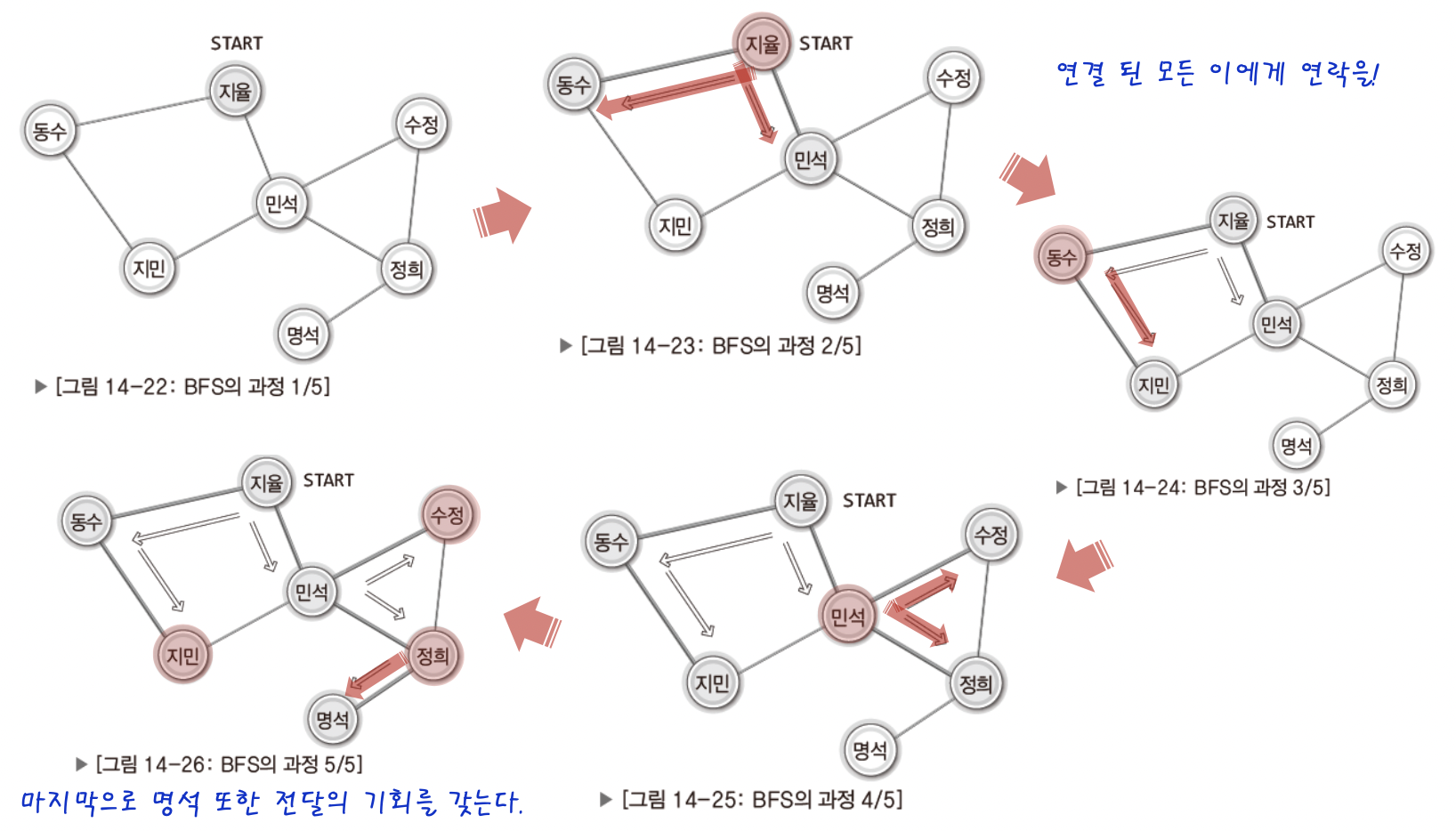

자신에게 연결된 모든 사람에게 연락을 취하는데 누가 먼저 연락을 취하느냐는 BFS 알고리즘적 관점에서 문제가 되지않는다! 어떠한 선택을 하건 잘 동작하기 때문이다.

이렇게 연락을 다하면 마지막에 명석이 연락을 취할 기회를 가지면서 BFS 는 끝이난다.

좋은 소문같은 경우는 BFS 라고 할수있다.
널리 널리 퍼뜨리자나!
그런데 비밀 이야기 "너한테만 하는 이야기..인데..." 는 DFS라고 할 수있다!!

BFS 구현 모델

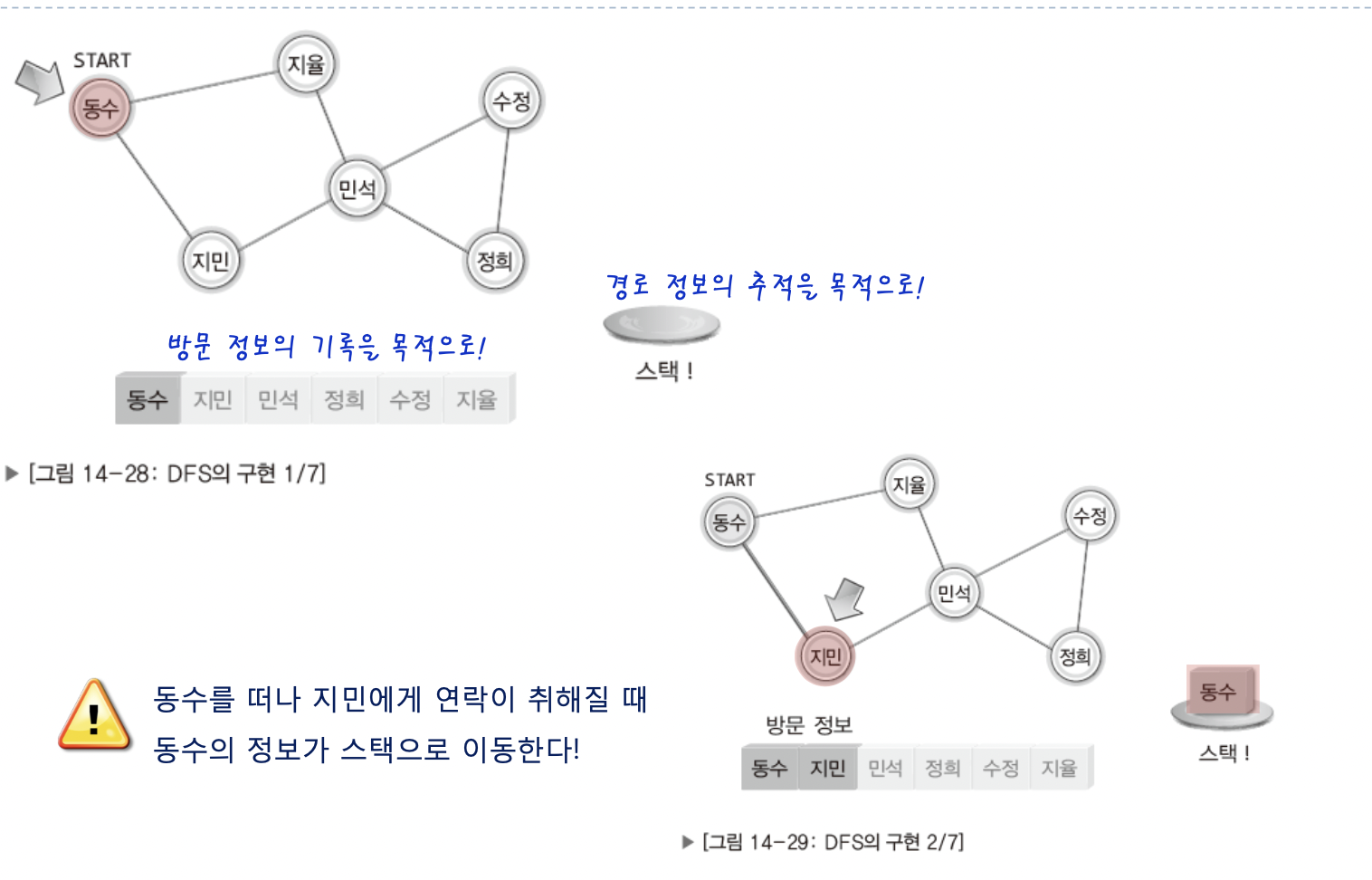
아까 스택일것이라고 이야기한것이 기억나는가!
그렇다!
DFS 구현에서는 두가지가 필요하다

• 스택 : 경로 정보의 추적을 목적
• 배열 : 방문 정보의 기록을 목적

동수는 시작과 동시에 방문 상태가 된다.
그렇게 지민에게 넘어가면 동수는 스택으로 옮긴다!
그리고 이렇게...
수정이에게 갈때까지 지나온 사람들을 스택에 쌓는데!!!
이제 더 이상 수정이가 연락을 취할 사람이 없어서
자신에게 연락한 사람에게 "야 넌 있냐?" 라고 전달해야한다!

그런데!! 자신에게 연락한 사람의 정보는 어디있는가!
바로 스택의 맨 위에 있다!
그 사람의 정보를 스택에서 POP 한다!!

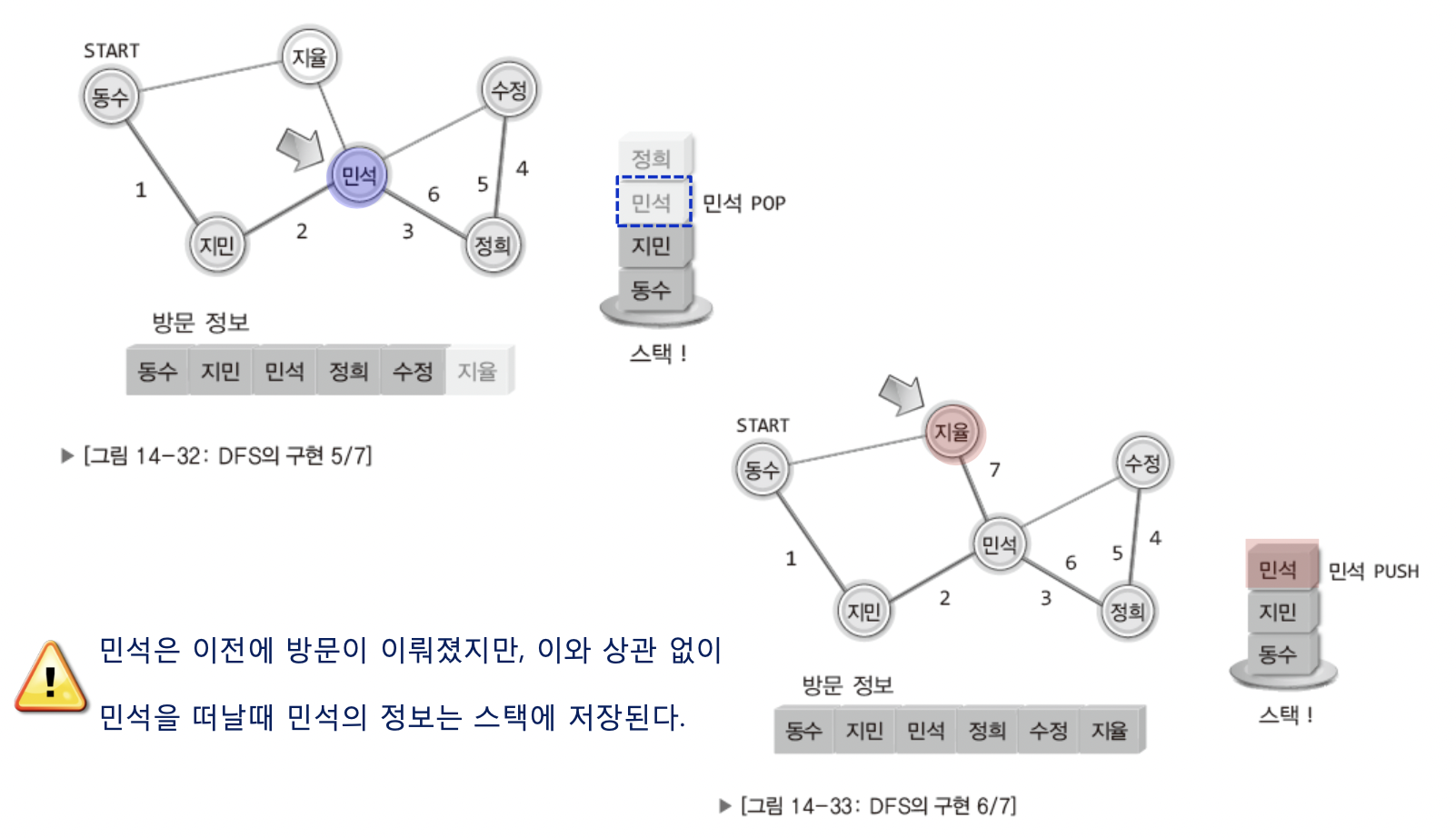
그렇게 민석까지 POP 하다 지율이가 연락을 못받았으니 지율이에게 연락을 한다!!
그런데!! 이제 모든 정점을 다 돌았고, 지율이에게는 이제 연락할 사람도 없다!
그리고 정점을 다 돌았으니 동수에게 회신이 가아햔다!!

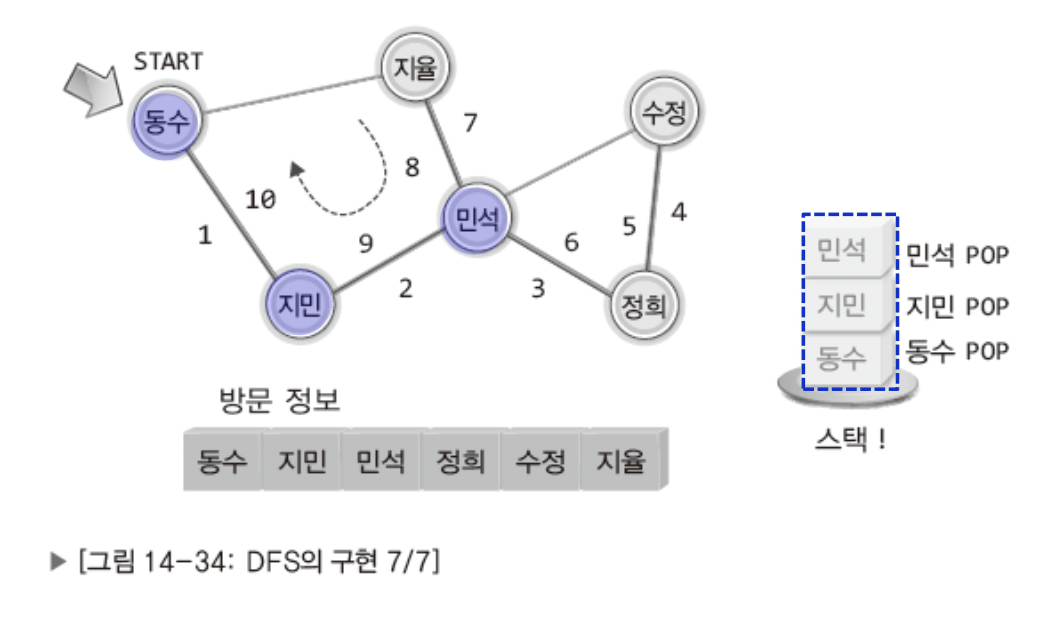
이때 스택의 모든 정보들을 POP 하여 동수에게 올 수 있다!!!

어떤가 !! 매우 간단하지 않는가!

스택은 DFS 알고리즘에 매우 중요한 역할을 하기에 스택의 용도를 이해하는것이 DFS알고리즘의 전부라고 해도 과언이 아니다.

다음 포스트에서 구현에 대해 배워보자 !