마지막은 그놈의 트리가 또 등장했다.
망할놈,,,.....
사실 트리는 그래프의 한 유형이기에 그래프에서 등장하는것이다.
사이클을 형성하지 않는 그래프

이와 같이 두개의 정점을 잇는 간선을 순서대로 나열한 것을 가리켜 "경로"라고 하고 동일한 간선을 중복하여 포함하지 않는 경로를 가리켜 "단순 경로"라 한다.
단순경로가 아닌 예는
b-a-c-b-a-d 와 같이 간선을 중복하여 포함하는 경로이다.
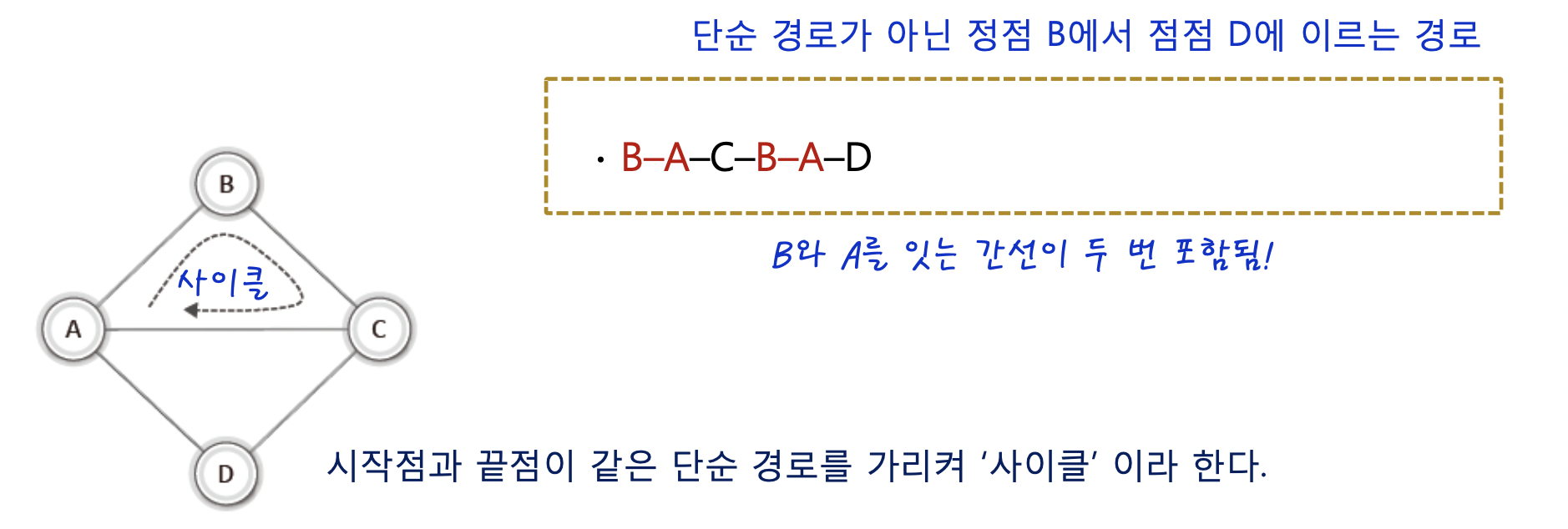
그런데 A-B-C-A 와 같이 다시 돌아오는 경로가 있다.
이는 단순경로가 아닐까?
맞다! 단순경로이다.
그저 돌아왔을뿐이지 이 경로가 중복된 간선을 지났는가?
아니다!
그렇다면 얘는 뭘까??
바로!!!!
단순 경로이면서 시작과 끝이 같은 경로를 가리켜 "사이클" 이라고 한다.
그렇다!!
저것은 사이클이다
그렇다면 사이클을 형상하지 않는 그래프도 있지 않을까?
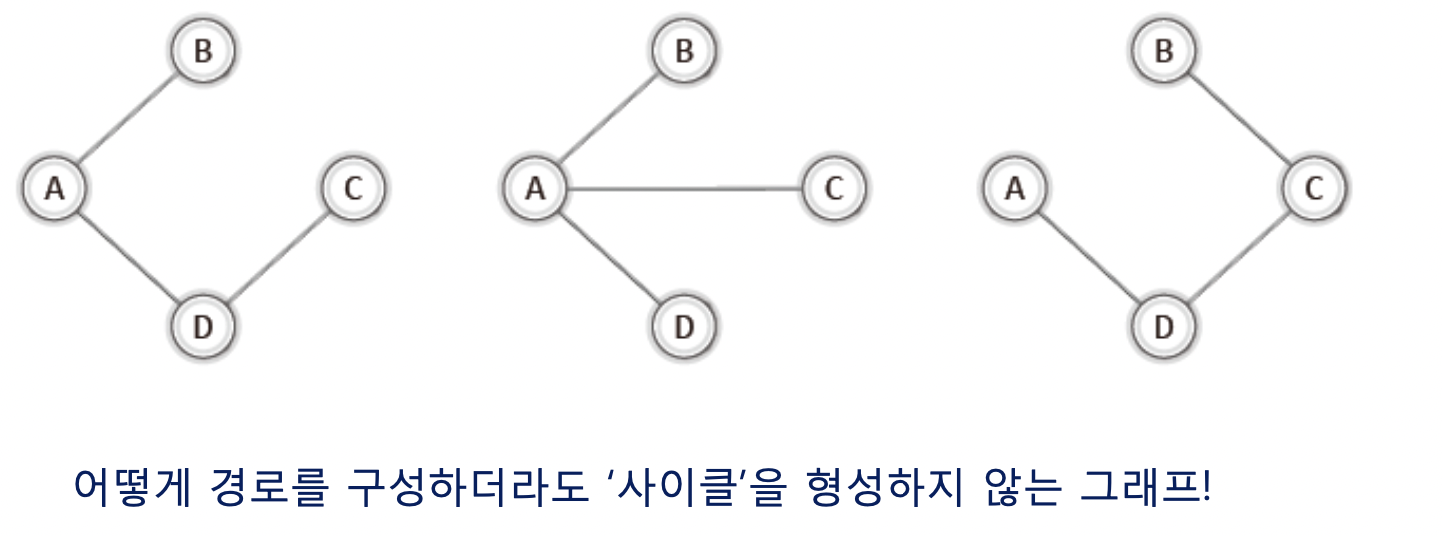
사이클이 되기 위해서는 단순경로이여야하는데 단순경로 조건을 만족시키면서 이 트리들을 사이클을 형성시킬수 없다.
그런데 이러한 그래프들..뭔가 많이 보지 않았는가?
한번 고개를 돌려보자!!!
사실 그는 어려우니
그래프를 돌려주겠다.
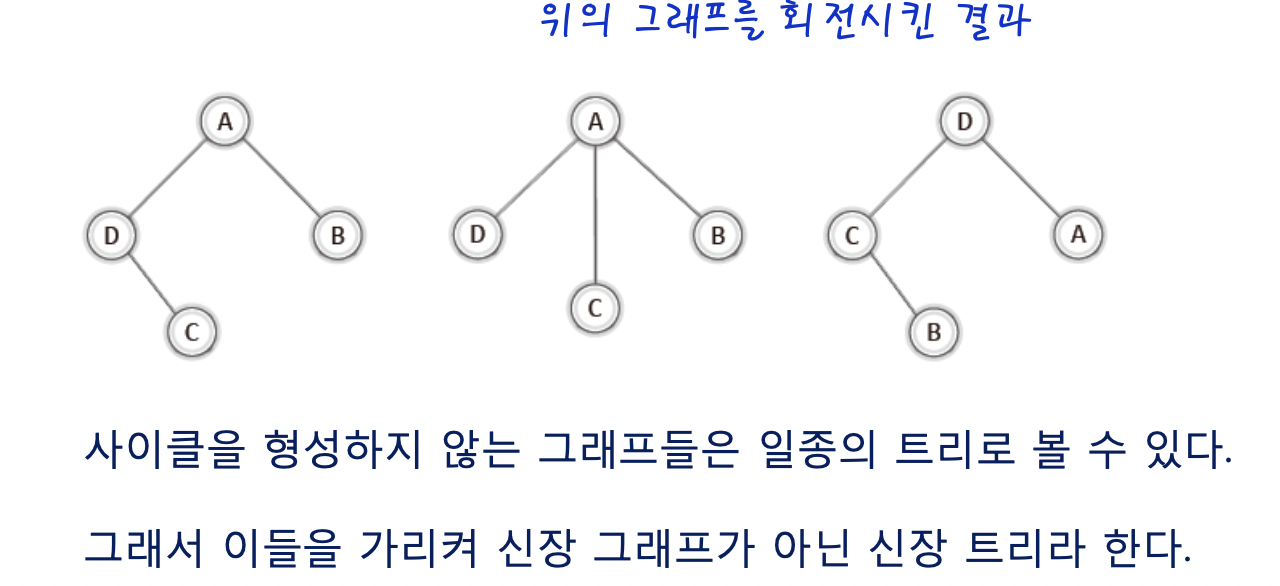
어떤가!!
그 놈의 트리가 여기서 등장한다.
우리는 이와 같이 사이클을 형성하지 않는 그래프를 "신장 트리"라고 한다.
최소 비용 신장 트리의 이해와 적용
신장 트리의 두 가지 조건은 다음과 같다.
- 그래프의 모든 정점이 간선에 의해서 하나로 연결되어있다.
- 그래프 내에서 사이클을 형성하지 않는다.
우리는 가중치 그래프를 대상으로 신장 트리를
아래의 그림과 같이 구성할 수 있다.
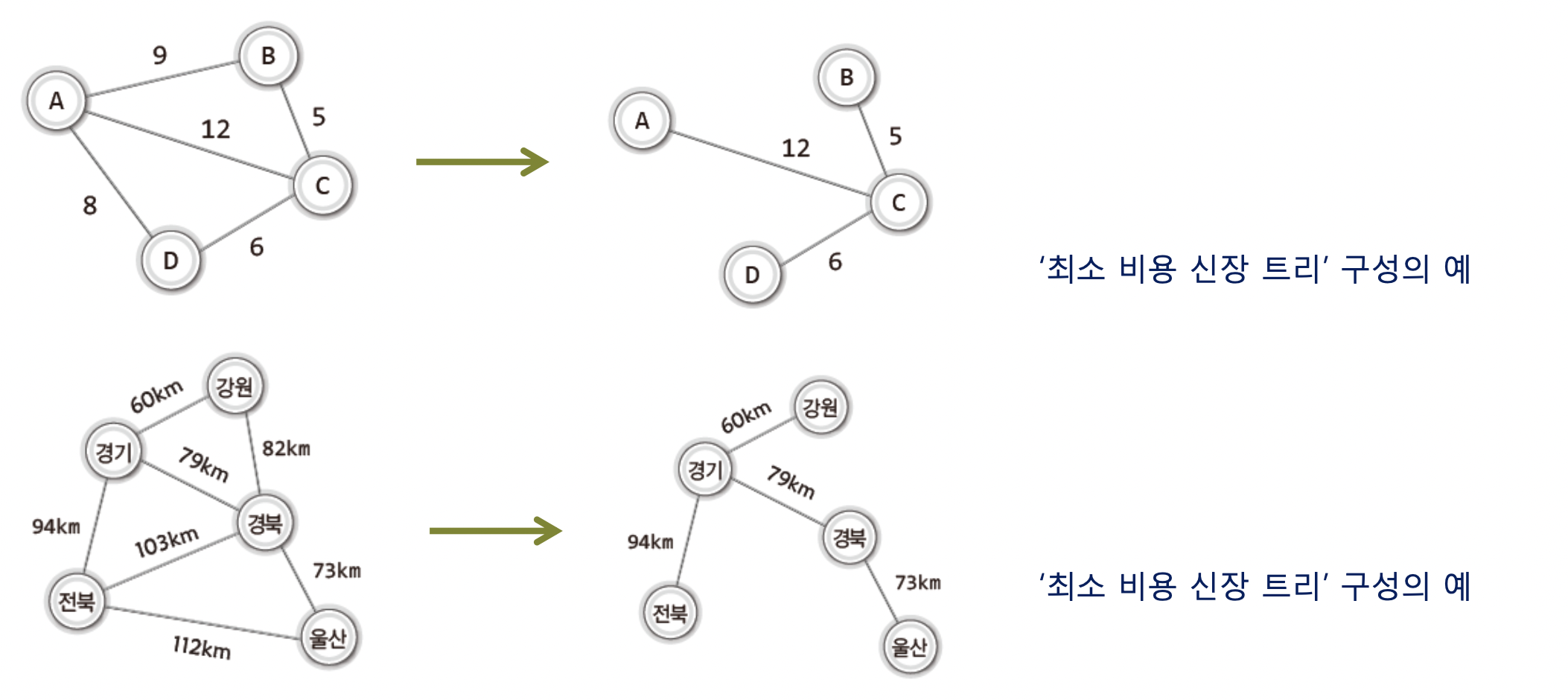
그리고 이 최소 비용 신장 트리를
Minimum spanning tree
줄여서 MST 라고 표현한다.
최소 비용 신장 트리의 구성을 위한 크루스칼 알고리즘 1
- 크루스칼 알고리즘
가중 치를 기준으로 간선을 정렬한 후에 MST가 될 때까지 간선을 하나씩 선택 또는 삭제해 나가는 방식- 프림 알고리즘
하나의 정점을 시작으로 MST가 될때까지 트리를 확장해 나가는 방식
이 외에도 많지만 지금은 하나의 알고리즘을 정확히 이해하고 이를 구현하는 경험이 더 의미있고 필요하므로
MST를 보다 더 대표하는 크루스칼 알고리즘을 배워보자.
이와 관련해서 그림을 한번 보자 !
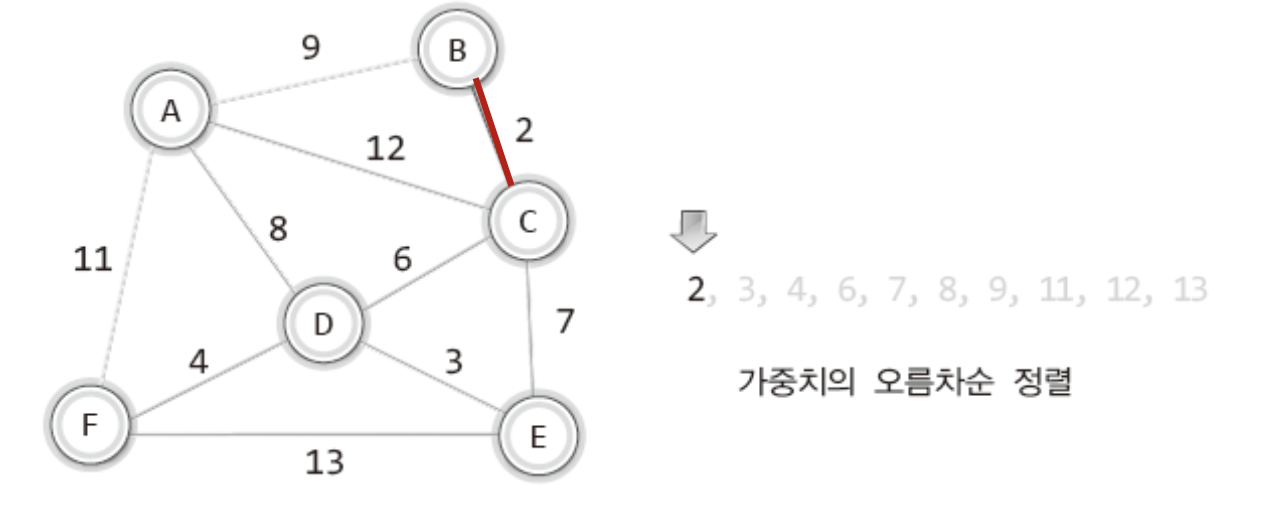
이런식으로 가중치를 기준으로 오름차순으로 정렬한다.
물론 정렬의 방식은 자신의 마음대로하면된다.
이런 식의 오름 차순으로 정렬된 가중치들의 간선을 하나씩 넣어보며 정점들을 간선으로 이어가는것이다.
그런데!!

이와 같이
가중치가 7인 간선이 연결되어야 할 타이밍에!!!
만약 7인 간선이 연결된다면 사이클이 형성되어 MST 조건을 망치게 된다!
그래서 패스하고 8을 연결시키는데...
이제 더 이상 진행하지 않는다.
그 이유는
간선의 수 + 1 = 정점의 수
이기 때문이다!
굳이..? 외울 필요는 없다.
그저 정점들을 그리고 최소 비용 신장트리의 기준에 맞게 연결해봐라!
모든 그래프는 이를 만족한다.
그럼 최종적으로 위의 그림대로 MST 가 맞춰진다
오름차순 크루스칼 알고리즘의 흐름에 있어서 핵심 사항은 다음과 같다.
- 가중치를 기준으로 간선을 오름차순으로 정렬한다.
- 낮은 가중치의 간선부터 시작해서 하나씩 그래프에 추가한다.
- 사이클을 형성하는 간선은 추가하지 않는다.
- 간선의 수가 정점의 수보다 하나 적을 때MST는 완성된다.
그러면 이제 내림차순을 스을~ 보자
최소 비용 신장 트리의 구성을 위한 크루스칼 알고리즘2
내림차순으로 정렬을 하면 낮은 가중치의 간선을 하나~씩 추가하는것이 아니라 높은 가중치의 간선을 하나~씩 빼는 방식으로 알고리즘이 전개된다!!
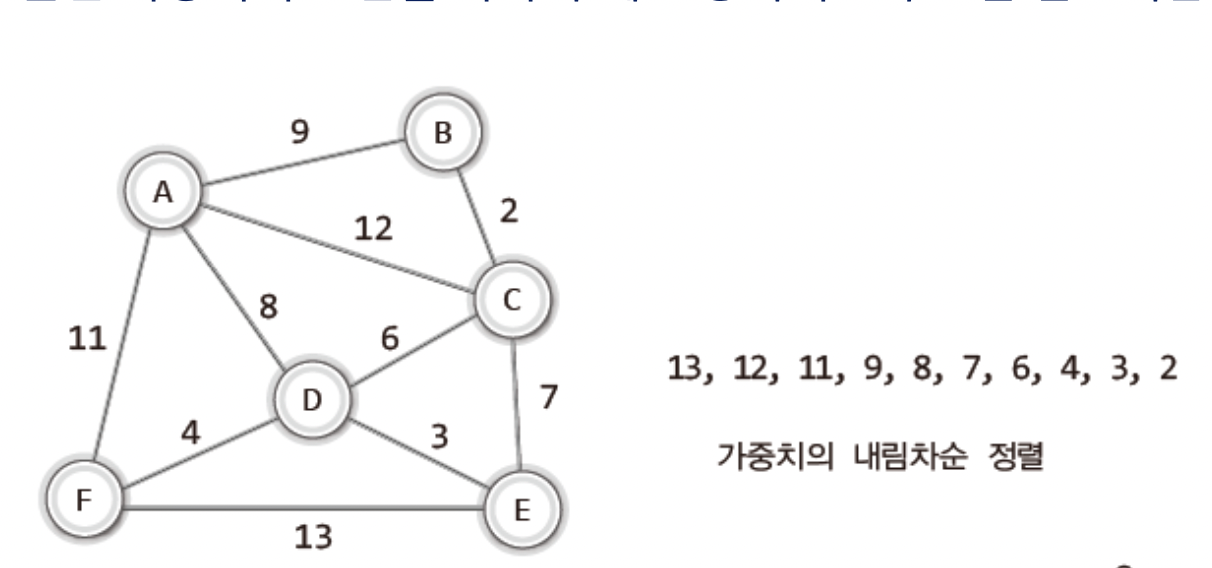
이렇게 가중치가 높은 간선들을 정렬한다.
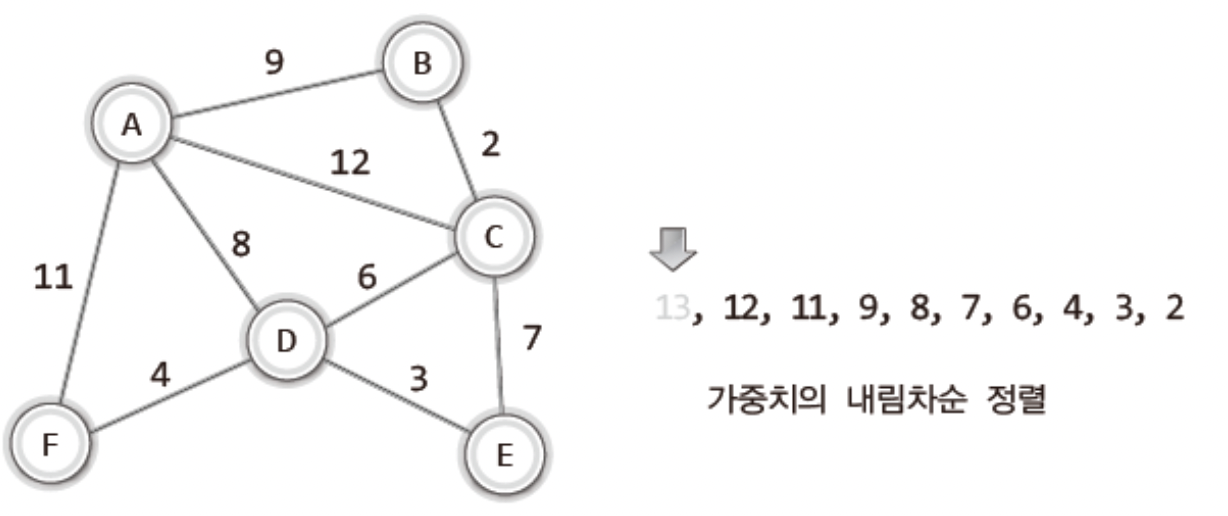
그리고 제일 높은 것들을 하나씩 빼가는데..

이렇게 쭉 진행하다가 !!!!
8을 빼면 A는 어떤 경로를 통해서도 닿지 않아 MST 조건을 위배하게된다!!
그러므로~
패스 한다!!
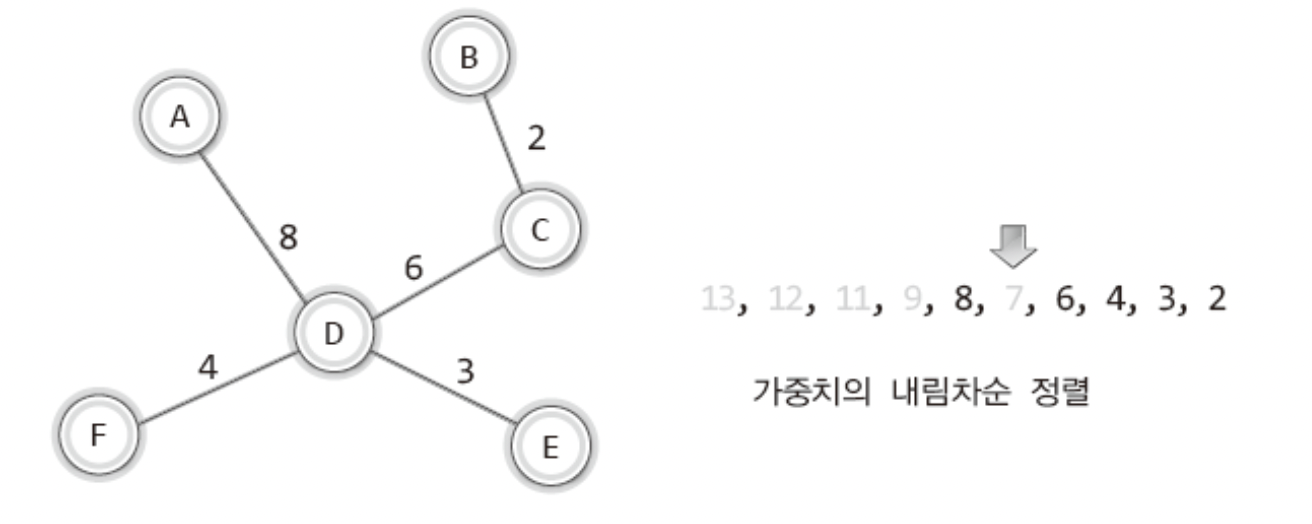
그렇게 패스하고 7을 제거하는데...
!!!!!
6개의 정점에 5개의 간선들이 연결됐다!!!
MST가 완성됐다!!
그럼 이 두번째 알고리즘의 핵심을 확인해보자.
- 가중치를 기준으로 간선을 내림차순으로 정렬한다.
- 높은 가중치의 간선부터 시작해서 하나씩 그래프에서 제거한다.
- 두 정점을 연결하는 다른 경로가 없을 경우 해당 간선은 제거하지 않는다.
- 간선의 수가 정점의 수보다 하나 적을 때 MST는 완성된다.
자 이제 기본 개념들을 배웠으니 다음포스트에 구현을 하고 이 자료구조를 마무리하겠다.
