크루스칼 알고리즘 구현을 위한 계획
크루스칼 알고리즘은 다음과 같다.
"가중치를 기준으로 간선을 내림차순으로 정렬한 다음 높은 가중치의 간선부터 시작해서 하나씩 그래프에서 제거하는 방식"
이전에 구현한 것들을 최대한 활용해보자!!!
이를 위해 DFS 구현결과인 다음 파일을 활용하자
- DLinkedList.h,c 연결리스트
- ArrayBaseStack.h,c 배열 기반 스택
ALGraphDFS.h,c 깊이 우선 탐색을 포함하는 그래프
이중 DFS 파일에 담겨 있는 대표적인 기능은
- 그래프의 구성
DFS 기반 정점 정보 출력
크루스칼 알고리즘을 구현 하기 앞서 그래프를 구성해야하기 때문에 이는 매우 유용하게 활용된다.
하지만 가중치 그래프를 구성해야해서 많은 부분을 수정해야한다.
그래서 수정한 파일의 이름을 ALGrpahKruskal.c,h 라고 하겠다.
그리고 이 알고리즘을 구현하기 위해서는
"이 간선을 삭제한 후에도 이 간선에 의해 연결된 두 정점을 연결하는 경로가 있는가?"
라는 질문에 답을 하는 함수를 먼저 준비해야 한다!
이를 위해 DFS 알고리즘을 활용하고 DFShowGraphVertex 함수를 확장할 생각이다.
그리고 가중치를 기준으로 간선을 정렬해야하므로
이를 위해 우선순위 큐를 활용할 생각이다 !
이는 앞서 구현한적있으니 파일또한 있다.
- PriorityQueue.h,c 우선순위 큐
UsefulHeap.h,c 우선순위 큐의 기반이 되는 힙
그리고 가중치가 포함된 간선의 정보를 담기 위한 구조체 정의 헤더파일을 추가해야한다.
- ALEdge.h 가중치가 포함된 간선의 표현을 위한 구조체 정의
그러므로 !
크루스칼 알고리즘을 구현하기 위해서는 다음과 같은 파일들이 필요하다.
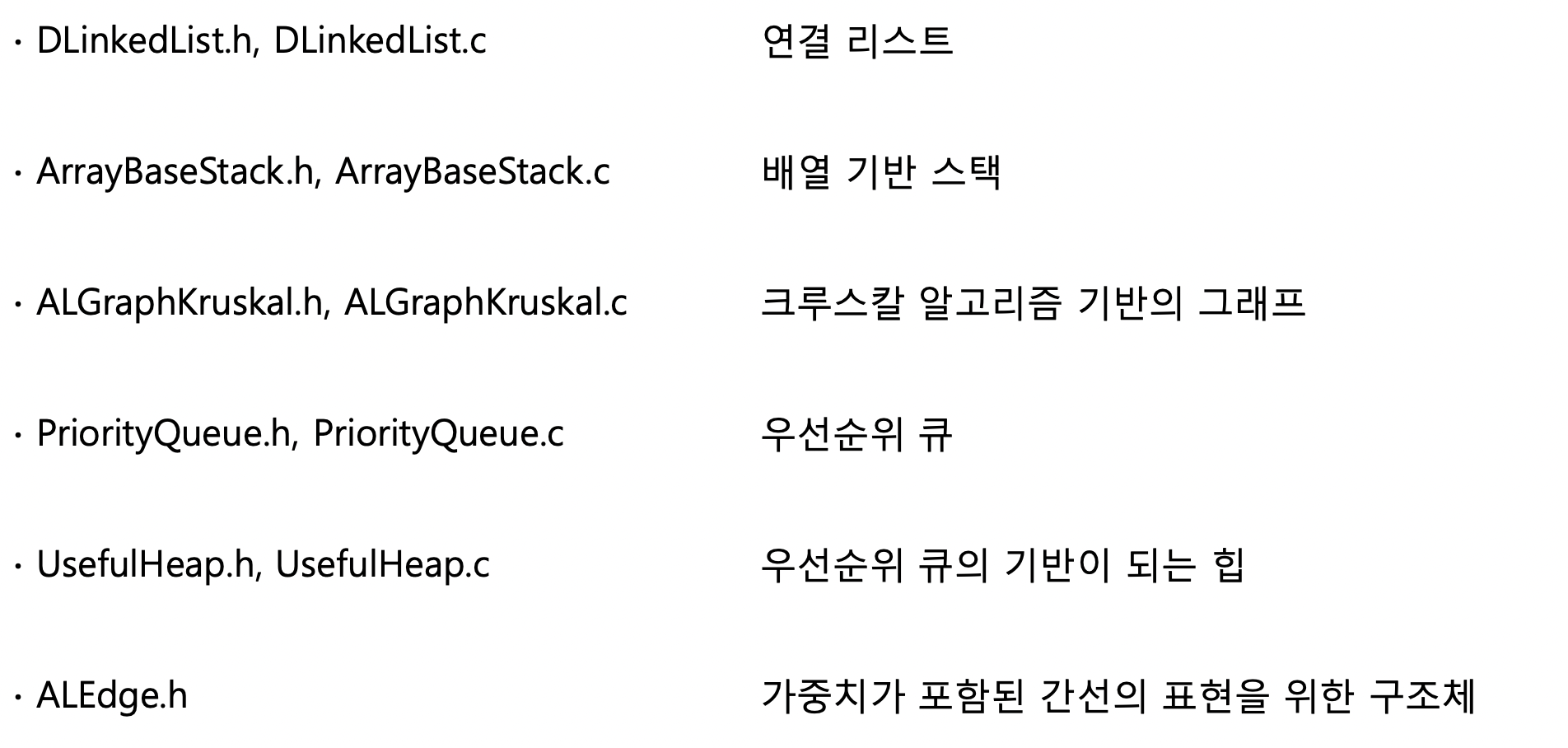
캬.... 우리가 이때까지 공부한것들의 종합세트이다!
자! 이제 구현해보자!!!
크루스칼 알고리즘의 구현
먼저 ALEdge.h 을 보여주겠다.
//
// ALEdge.h
// ALGraphKruskal
//
// Created by 서희찬 on 2021/04/25.
//
#ifndef ALEdge_h
#define ALEdge_h
typedef struct _edge{
int v1; // 간선이 연결하는 첫 번째 정점
int v2; // 간선이 연결하는 두 번째 정점
int weight; // 간선의 가중치
}Edge;
#endif /* ALEdge_h */사실!! 이 구조체의 목적은 "간선 정보의 저장"이 아니라
"간선의 가중치 정보 저장"
이다!
이렇게 별도로 저장하는 이유는
이 정보를 이용하여 가중치 기반의 정렬을 진행하기 위함이다.
이어서 ALGraphKruskal.h 파일을 보자.
//
// ALGraphKruskal.h
// ALGraphKruskal
//
// Created by 서희찬 on 2021/04/25.
//
#ifndef ALGraphKruskal_h
#define ALGraphKruskal_h
#include "PriorityQueue.h"
#include "DLinkedList.h"
#include "ALEdge.h"
// 정점의 이름 상수화
enum {A,B,C,D,E,F,G,H,I,J};
typedef struct _ual{
int numV; // 정점의 수
int numE; // 간선의 수
List * adjList; // 간선의 정보
int * visitInfo;
PQueue pqueue; // 간선의 가중치 정보 저장
}ALGraph;
//그래프의 초기화
void GraphInit(ALGraph * pg , int nv);
//그래프의 리소스 해제
void GraphDestroy(ALGraph * pg);
//간선의 추가
void AddEdge(ALGraph * pg, int fromV, int toV,int weight);
// 간선의 정보 출력
void ShowGraphEdgeInfo(ALGraph * pg);
// 정점의 정보 출력 : DFS 기반
void DFShowGraphVertex(ALGraph * pg, int startV);
// 새로운 함수
void ConKruskalMST(ALGraph * pg); // 최소 비용 신장 트리의 구성
//새로운 함수
void ShowGraphEdgeWeightInfo(ALGraph * pg); // 가중치 정보 출력
#endif /* ALGraphKruskal_h */우선 GraphInit 함수부터 수정해주자.
int PQWeightComp(Edge d1, Edge d2)
{
return d1.weight - d2.weight;
}
void GraphInit(ALGraph * pg, int nv) // 그래프의 초기화
{
int i;
// 정점의 수에 해당하는 길이의 리스트 배열을 생성하낟.
pg->adjList = (List*)malloc(sizeof(List)*nv); // 간선정보를 저장할 리스트 생성
pg->visitInfo = (int*)malloc(sizeof(int)*pg->numV); // 정점의 수를 길이로 하여 배열을 할당
pg->numV = nv; // 정점의 수는 nv에 저장된 값으로 결정
pg->numE=0;// 초기의 간선수는 0개
memset(pg->visitInfo,0,sizeof(int)*pg->numV);
// 정점의 수만큼 생성된 리스트들을 초기화한다.
for(i=0;i<nv;i++)
{
ListInit(&(pg->adjList[i]));
SetSortRule(&(pg->adjList[i]), WhoIsPrecede); //정렬기준유도
}
//우선 순위 큐의 초기화
PQueueInit(&(pg->pqueue), PQWeightComp);
}우선순위 큐를 초기화 해주는 코드를 작성해주었다.
그래서 PQWeightComp 함수를 작성해줌으로써 첫 번째 인자로 전달된 간선의 가중치가 클 때 양수가 반환 되도록 정의 하였다.
따라서 가중치를 기준으로 내림차순 으로 간선의 정보를 꺼낼 수 있게 됐다!!!
이것이 크루스칼 알고리즘의 구현을 위한 것이다.
이어서 AddEdge 함수를 보자
void AddEdge(ALGraph * pg, int fromV, int toV,int weight)
{
Edge edge = {fromV, toV, weight}; // 간선의 가중치 정보를 담음
// 정점 form V의 연결 리스트에 정점 toV 의 정보 추가
LInsert(&(pg->adjList[fromV]), toV);
// 정점 toV의 연결 리스트에 정점 fromV의 정보 추가
LInsert(&(pg->adjList[toV]), fromV);
pg->numE+=1;
// 간선의 가중치 정보를 우선순의 큐에 저장
PEnqueue(&(pg->pqueue), edge);
}우선순위 큐의 저장 대상이 구조체 Edge의 변수 이므로 UsefulHeap.h 에
ALEdge.h 파일을 포함시키고
typedef Edge HData; 로 변경 해주어야한다.
이제 void ConKruskalMST(ALGrpah * pg);
를 짜주는데
이 함수를 호출하면서 그래프의 주소 값을 전달하면, 전달된 주소 값의 그래프는 최소 비용 신장 트리가 된다.
크루스칼 알고리즘을 담은 함수의 정의
void ConKruskalMST(ALGraph * pg) // 최소 비용 신장 트리를 구성하는 함수
{
Edge recvEdge[20]; // 복원할 간선의 정보 저장
Edge edge;
int eidx = 0;
int i;
// MST를 형성할 때까지 아래의 반복문 실행
while(pg->numE+1 > pg -> numV) // MST 간선의 수 + 1 == 정점의 수
{
edge = PDequeue(&(pg->pqueue));
RemoveEdge(pg,edge.v1,edge.v2);
if(!IsConnVertex(pg,edge.v1,edge.v2))
{
RecoverEdge(pg,edge.v1,edge.v2,edge.weight);
recvEdge[eidx++] = edge;
}
}
// 우선순위 큐에서 삭제된 간선의 정보를 회복
for(i=0;i<eidx;i++)
PEnqueue(&(pg->pqueue), recvEdge[i]);
}여기서 아직 정의 하지 않은 함수들이 있다.
- RemoveEdge : 그래프에서 간선을 삭제한다.
- IsConnVertex : 두 정점이 연결되어 있는지 확인한다.
- RecoverEdge : 삭제된 간선을 다시 삽입한다.
이를 설명하기 앞서
반복문을 주석을 통해 자세히 보자.
void ConKruskalMST(ALGraph * pg) // 최소 비용 신장 트리를 구성하는 함수
{
Edge recvEdge[20]; // 복원할 간선의 정보 저장
Edge edge;
int eidx = 0;
int i;
// MST를 형성할 때까지 아래의 반복문 실행
while(pg->numE+1 > pg -> numV) // MST 간선의 수 + 1 == 정점의 수
{
// 우선순위 큐에서 가중치가 제일 높은 간선의 정보를 꺼낸다.
edge = PDequeue(&(pg->pqueue));
// 우선순위 큐에서 꺼낸 간선을 실제로 그래프에서 삭제한다.
RemoveEdge(pg,edge.v1,edge.v2);
// 간선을 삭제하고 나서도 두 정점을 연결하는 경로가 있는지 확인한다.
if(!IsConnVertex(pg,edge.v1,edge.v2))
{
// 경로가 없다면 삭제한 간선을 다시 살린다.
RecoverEdge(pg,edge.v1,edge.v2,edge.weight);
// 복원한 간선의 정보를 별도로 저장한다.
recvEdge[eidx++] = edge;
}
}이때 복원한 간선의 정보를 별도로 저장하는 이유는
우선순위 큐에 다시 넣으면 PDequeue 함수 호출 시 다시 꺼내게 된다!!
크루스칼 알고리즘은 한번 검토가 이뤄진 간선을 재검토 하지 않기에 복원된 간선을 다시 넣으면안되서 별도로 저장하는것이다.
그렇게 반복문이 끝난후 이것을 다시 넣는다!!
// 우선순위 큐에서 삭제된 간선의 정보를 회복
for(i=0;i<eidx;i++)
PEnqueue(&(pg->pqueue), recvEdge[i]);
}
이렇게 위의 반복문이 실행하게 되면 우선순위 큐에는 MST를 이루는 간선의 정보만 남게 된다.
그리고 이정보를 출력하기 위해
void ShowGraphEdgeWeightInfo(ALGraph * pg) // 간선의 가중치 정보 출력
{
PQueue copyPQ = pg -> pqueue;
Edge edge;
while(!PQIsEmpty(©PQ))
{
edge = PDequeue(©PQ)
printf("(%c ~ %c, w:%d \n", edge.v1+65,edge.v2+65,edge.weight);
}이 함수가 필요하다
그럼 위에서 설명 안한 함수들을 짜주자.
void RemoveEdge(ALGraph * pg, int fromV, int toV) // 간선의 소멸
{
RemoveWayEdge(pg, fromV, toV);
RemoveWayEdge(pg, toV, fromV);
(pg->numE)--;
}
void RemoveWayEdge(ALGraph * pg, int fromV, int toV) // 한쪽 방향의 간선 소멸
{
int edge;
if(LFirst(&(pg->adjList[fromV]), &edge))
{
if(edge==toV)
{
LRemove(&(pg->adjList[fromV]));
return;
}
while(LNext(&(pg->adjList[fromV]), &edge))
{
if(edge==toV){
LRemove(&(pg->adjList[fromV]));
return;
}
}
}
}
우리는 무방향 그래프 이다 보니 소멸시킬 간선의 정보가 두개이다!
이제 복원함수를 보자
void RecoverEdge(ALGraph * pg, int fromV, int toV, int weight)
{
LInsert(&(pg->adjList[fromV]), toV);
LInsert(&(pg->adjList[toV]), fromV);
(pg->numE)++;
}마지막으로 IsconnVertex 함수는
두 정점이 연결되어있나~? 확인하는 함수인데
이 함수는 DFShowGraphVertex 함수처럼 정점들을 돌아다니며 확인할것이니
기존에 짜준 이 함수에서 살짝 ~ 변형만 해주면 된다.
int IsConnVertex(ALGraph * pg, int v1, int v2)
{
// 시작 정점의 방문이 일어난다 !
Stack stack;
int visitV = v1; // 1
int nextV;
StackInit(&stack); // DFS를 위한 스택의 초기화
VisitVertex(pg, visitV); // 시작 정점을 방문
SPush(&stack, visitV); // 시작 정점의 정보를 스택으로 !
// visitV에 담긴 정점과 연결된 정점의 방문을 시도하는 while 문
while(LFirst(&(pg->adjList[visitV]), &nextV)== TRUE)
// LFirst 를 통해서 visitV에 연결된 정점 하나를 얻는다.
// 이렇게 해서 얻은 정점의 정보는 nextV에 저장된다.
{
// visitV와 연결된 정점의 정보가 nextV에 담긴 상태에서 이하를 진행
int visitFlag = FALSE;
// 정점을 돌아다니는 도중에 목표를 찾는다면 트루를 반환
if(nextV == v2)
{
// 함수가 반환되기 전에 초기화 진행
memset(pg->visitInfo, 0, sizeof(int)*pg->numV);
return TRUE; // 목표 찾았으니 트루 반환
}
// nextV에 담긴 정점의 정보를 가지고 방문을 시도한다.
if(VisitVertex(pg, nextV)== TRUE) // 방문에 성공했다면
{
// 방문 성공했으니 visitV의 정보는 스택에 푸쉬
SPush(&stack, visitV); // visitV 담긴 내용을 PUSH
// nextV에 담긴 정보를. visitV 에 담고 다시 반복문
// 반복문을 다시 시작하는 것은 또 다른 정점의 방문을 시도하는 것 !
visitV = nextV;
visitFlag = TRUE;
}
// LFirst 함수를 통해서 얻은 정점의 방문에 실패한 경우 이하 실행
else // 방문 실패.. 연결된 다른 정점들을 찾는다.
{
//아래의 반목은 visitV에 연결된 정점을 찾을 때 까지 반복된다.
while(LNext(&(pg->adjList[visitV]), &nextV)== TRUE)
{
//LNext 함수의 호출을 통해서 visitV에 연결된 정점 하나를 얻는다.
// 이렇게 얻은 정점의 정보는 nextV에 저장된다.
if(nextV == v2)
{
memset(pg->visitInfo, 0, sizeof(int)*pg->numV);
return TRUE;
}
// 이 정보를 바탕으로 방문을 시도한다.
if(VisitVertex(pg, nextV) == TRUE)
{
SPush(&stack, visitV); // 방문 성공했으니 푸쉬
visitV = nextV; // 담고 브레윀!
visitFlag = TRUE;
break;
}
}
}
// 정점 방문에 실패했다면 그에 따른 처리를 진행한다.
if(visitFlag == FALSE) // 추가로 방문한 정점이 없었다면
{
// 길을 되돌아 가거나 시작 위치로 되돌아와서 프로그램을 종료하거나
if(SIsEmpty(&stack)== TRUE) // 시작점으로 되돌아 왔음
break;
else
visitV = SPop(&stack); // 길을 되돌아간다
}
}
// 이후의 탐색을 위해서 탐색 정보 초기화
memset(pg->visitInfo, 0, sizeof(int)*pg->numV);
return FALSE; // 목표를 찾지 못했다 !
}
그렇다!!!
그저 연결된 간선을 찾는다면 맴버를 초기화 해주고 참을 반환해주고 그렇지 않다면 마지막에 FALSE를 반환해준다.
그럼 전체 소스파일을 보자
ALGraphKruskal.c
//
// ALGraphKruskal.c
// ALGraphKruskal
//
// Created by 서희찬 on 2021/04/25.
//
#include "ALGraphKruskal.h"
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include "DLinkedList.h"
#include "ArrayBaseStack.h"
void RemoveWayEdge(ALGraph * pg, int fromV, int toV) // 한쪽 방향의 간선 소멸
{
int edge;
if(LFirst(&(pg->adjList[fromV]), &edge))
{
if(edge==toV)
{
LRemove(&(pg->adjList[fromV]));
return;
}
while(LNext(&(pg->adjList[fromV]), &edge))
{
if(edge==toV){
LRemove(&(pg->adjList[fromV]));
return;
}
}
}
}
void RemoveEdge(ALGraph * pg, int fromV, int toV) // 간선의 소멸
{
RemoveWayEdge(pg, fromV, toV);
RemoveWayEdge(pg, toV, fromV);
(pg->numE)--;
}
void RecoverEdge(ALGraph * pg, int fromV, int toV, int weight)
{
LInsert(&(pg->adjList[fromV]), toV);
LInsert(&(pg->adjList[toV]), fromV);
(pg->numE)++;
}
int WhoIsPrecede(int data1,int data2);
int PQWeightComp(Edge d1, Edge d2)
{
return d1.weight - d2.weight;
}
void GraphInit(ALGraph * pg, int nv) // 그래프의 초기화
{
int i;
// 정점의 수에 해당하는 길이의 리스트 배열을 생성하낟.
pg->adjList = (List*)malloc(sizeof(List)*nv); // 간선정보를 저장할 리스트 생성
pg->visitInfo = (int*)malloc(sizeof(int)*pg->numV); // 정점의 수를 길이로 하여 배열을 할당
pg->numV = nv; // 정점의 수는 nv에 저장된 값으로 결정
pg->numE=0;// 초기의 간선수는 0개
memset(pg->visitInfo,0,sizeof(int)*pg->numV);
// 정점의 수만큼 생성된 리스트들을 초기화한다.
for(i=0;i<nv;i++)
{
ListInit(&(pg->adjList[i]));
SetSortRule(&(pg->adjList[i]), WhoIsPrecede); //정렬기준유도
}
//우선 순위 큐의 초기화
PQueueInit(&(pg->pqueue), PQWeightComp);
}
void GraphDestroy(ALGraph * pg)
{
if(pg->adjList != NULL)
free(pg->adjList); // 동적으로 할당된 연결 리스트의 소멸
if(pg->visitInfo != NULL)
free(pg->visitInfo);
}
void AddEdge(ALGraph * pg, int fromV, int toV,int weight)
{
Edge edge = {fromV, toV, weight}; // 간선의 가중치 정보를 담음
// 정점 form V의 연결 리스트에 정점 toV 의 정보 추가
LInsert(&(pg->adjList[fromV]), toV);
// 정점 toV의 연결 리스트에 정점 fromV의 정보 추가
LInsert(&(pg->adjList[toV]), fromV);
pg->numE+=1;
// 간선의 가중치 정보를 우선순의 큐에 저장
PEnqueue(&(pg->pqueue), edge);
}
void ShowGraphEdgeInfo(ALGraph * pg)
{
int i;
int vx;
for (i=0; i<pg->numV; i++) { // for 문을 돌면서 리스트의 모든 키에 접근한다.
printf("%c 와 연결된 정점 : ",i + 65); // 아스키코드로 !
if(LFirst(&(pg->adjList[i]), &vx)) //vx에 저장된다.
{
printf("%c ",vx+65);
while(LNext(&(pg->adjList[i]), &vx)) // 연결된 노드가 있다면 출력
printf("%c ",vx+65);
}
printf("\n");
}
}
int WhoIsPrecede(int data1, int data2)
{
if(data1<data2)
return 0;
else
return 1;
}
int VisitVertex(ALGraph * pg, int visitV)
{
if(pg->visitInfo[visitV]==0) // visitV에 처음 방문일 때 '참' 인 이프문
{
pg->visitInfo[visitV] = 1; // 방문한것으로 기록
//printf("%c ", visitV+65); //방문 정점 이름 출력
return TRUE; // 방문 성공
}
return FALSE; // 방문 실패
}
// DFS -> 정점의 정보 출력
void DFShowGraphVertex(ALGraph * pg, int startV)
{
// 시작 정점의 방문이 일어난다 !
Stack stack;
int visitV = startV;
int nextV;
StackInit(&stack); // DFS를 위한 스택의 초기화
VisitVertex(pg, visitV); // 시작 정점을 방문
SPush(&stack, visitV); // 시작 정점의 정보를 스택으로 !
// visitV에 담긴 정점과 연결된 정점의 방문을 시도하는 while 문
while(LFirst(&(pg->adjList[visitV]), &nextV)== TRUE)
// LFirst 를 통해서 visitV에 연결된 정점 하나를 얻는다.
// 이렇게 해서 얻은 정점의 정보는 nextV에 저장된다.
{
// visitV와 연결된 정점의 정보가 nextV에 담긴 상태에서 이하를 진행
int visitFlag = FALSE;
// nextV에 담긴 정점의 정보를 가지고 방문을 시도한다.
if(VisitVertex(pg, nextV)== TRUE) // 방문에 성공했다면
{
// 방문 성공했으니 visitV의 정보는 스택에 푸쉬
SPush(&stack, visitV); // visitV 담긴 내용을 PUSH
// nextV에 담긴 정보를. visitV 에 담고 다시 반복문
// 반복문을 다시 시작하는 것은 또 다른 정점의 방문을 시도하는 것 !
visitV = nextV;
visitFlag = TRUE;
}
// LFirst 함수를 통해서 얻은 정점의 방문에 실패한 경우 이하 실행
else // 방문 실패.. 연결된 다른 정점들을 찾는다.
{
//아래의 반목은 visitV에 연결된 정점을 찾을 때 까지 반복된다.
while(LNext(&(pg->adjList[visitV]), &nextV)== TRUE)
{
//LNext 함수의 호출을 통해서 visitV에 연결된 정점 하나를 얻는다.
// 이렇게 얻은 정점의 정보는 nextV에 저장된다.
// 이 정보를 바탕으로 방문을 시도한다.
if(VisitVertex(pg, nextV) == TRUE)
{
SPush(&stack, visitV); // 방문 성공했으니 푸쉬
visitV = nextV; // 담고 브레윀!
visitFlag = TRUE;
break;
}
}
}
// 정점 방문에 실패했다면 그에 따른 처리를 진행한다.
if(visitFlag == FALSE) // 추가로 방문한 정점이 없었다면
{
// 길을 되돌아 가거나 시작 위치로 되돌아와서 프로그램을 종료하거나
if(SIsEmpty(&stack)== TRUE) // 시작점으로 되돌아 왔음
break;
else
visitV = SPop(&stack); // 길을 되돌아간다
}
}
// 이후의 탐색을 위해서 탐색 정보 초기화
memset(pg->visitInfo, 0, sizeof(int)*pg->numV);
}
int IsConnVertex(ALGraph * pg, int v1, int v2)
{
// 시작 정점의 방문이 일어난다 !
Stack stack;
int visitV = v1; // 1
int nextV;
StackInit(&stack); // DFS를 위한 스택의 초기화
VisitVertex(pg, visitV); // 시작 정점을 방문
SPush(&stack, visitV); // 시작 정점의 정보를 스택으로 !
// visitV에 담긴 정점과 연결된 정점의 방문을 시도하는 while 문
while(LFirst(&(pg->adjList[visitV]), &nextV)== TRUE)
// LFirst 를 통해서 visitV에 연결된 정점 하나를 얻는다.
// 이렇게 해서 얻은 정점의 정보는 nextV에 저장된다.
{
// visitV와 연결된 정점의 정보가 nextV에 담긴 상태에서 이하를 진행
int visitFlag = FALSE;
// 정점을 돌아다니는 도중에 목표를 찾는다면 트루를 반환
if(nextV == v2)
{
// 함수가 반환되기 전에 초기화 진행
memset(pg->visitInfo, 0, sizeof(int)*pg->numV);
return TRUE; // 목표 찾았으니 트루 반환
}
// nextV에 담긴 정점의 정보를 가지고 방문을 시도한다.
if(VisitVertex(pg, nextV)== TRUE) // 방문에 성공했다면
{
// 방문 성공했으니 visitV의 정보는 스택에 푸쉬
SPush(&stack, visitV); // visitV 담긴 내용을 PUSH
// nextV에 담긴 정보를. visitV 에 담고 다시 반복문
// 반복문을 다시 시작하는 것은 또 다른 정점의 방문을 시도하는 것 !
visitV = nextV;
visitFlag = TRUE;
}
// LFirst 함수를 통해서 얻은 정점의 방문에 실패한 경우 이하 실행
else // 방문 실패.. 연결된 다른 정점들을 찾는다.
{
//아래의 반목은 visitV에 연결된 정점을 찾을 때 까지 반복된다.
while(LNext(&(pg->adjList[visitV]), &nextV)== TRUE)
{
//LNext 함수의 호출을 통해서 visitV에 연결된 정점 하나를 얻는다.
// 이렇게 얻은 정점의 정보는 nextV에 저장된다.
if(nextV == v2)
{
memset(pg->visitInfo, 0, sizeof(int)*pg->numV);
return TRUE;
}
// 이 정보를 바탕으로 방문을 시도한다.
if(VisitVertex(pg, nextV) == TRUE)
{
SPush(&stack, visitV); // 방문 성공했으니 푸쉬
visitV = nextV; // 담고 브레윀!
visitFlag = TRUE;
break;
}
}
}
// 정점 방문에 실패했다면 그에 따른 처리를 진행한다.
if(visitFlag == FALSE) // 추가로 방문한 정점이 없었다면
{
// 길을 되돌아 가거나 시작 위치로 되돌아와서 프로그램을 종료하거나
if(SIsEmpty(&stack)== TRUE) // 시작점으로 되돌아 왔음
break;
else
visitV = SPop(&stack); // 길을 되돌아간다
}
}
// 이후의 탐색을 위해서 탐색 정보 초기화
memset(pg->visitInfo, 0, sizeof(int)*pg->numV);
return FALSE; // 목표를 찾지 못했다 !
}
void ConKruskalMST(ALGraph * pg) // 최소 비용 신장 트리를 구성하는 함수
{
Edge recvEdge[20]; // 복원할 간선의 정보 저장
Edge edge;
int eidx = 0;
int i;
// MST를 형성할 때까지 아래의 반복문 실행
while(pg->numE+1 > pg -> numV) // MST 간선의 수 + 1 == 정점의 수
{
// 우선순위 큐에서 가중치가 제일 높은 간선의 정보를 꺼낸다.
edge = PDequeue(&(pg->pqueue));
// 우선순위 큐에서 꺼낸 간선을 실제로 그래프에서 삭제한다.
RemoveEdge(pg,edge.v1,edge.v2);
// 간선을 삭제하고 나서도 두 정점을 연결하는 경로가 있는지 확인한다.
if(!IsConnVertex(pg,edge.v1,edge.v2))
{
// 경로가 없다면 삭제한 간선을 다시 살린다.
RecoverEdge(pg,edge.v1,edge.v2,edge.weight);
// 복원한 간선의 정보를 별도로 저장한다.
recvEdge[eidx++] = edge;
}
}
// 우선순위 큐에서 삭제된 간선의 정보를 회복
for(i=0;i<eidx;i++)
PEnqueue(&(pg->pqueue), recvEdge[i]);
}
void ShowGraphEdgeWeightInfo(ALGraph * pg) // 간선의 가중치 정보 출력
{
PQueue copyPQ = pg -> pqueue;
Edge edge;
while(!PQIsEmpty(©PQ))
{
edge = PDequeue(©PQ);
printf("(%c ~ %c, w:%d \n", edge.v1+65,edge.v2+65,edge.weight);
}
}
자 ! 이제 메인 함수를 짜고 실행결과를 보자.
//
// main.c
// ALGraphKruskal
//
// Created by 서희찬 on 2021/04/25.
//
#include <stdio.h>
#include "ALGraphKruskal.h"
int main(void)
{
ALGraph graph;
GraphInit(&graph, 6);
AddEdge(&graph, A, B, 9);
AddEdge(&graph, B, C, 2);
AddEdge(&graph, A, C, 12);
AddEdge(&graph, A, D, 8);
AddEdge(&graph, D, C, 6);
AddEdge(&graph, A, F, 11);
AddEdge(&graph, F, D, 4);
AddEdge(&graph, D, E, 3);
AddEdge(&graph, E, C, 7);
AddEdge(&graph, F, E, 13);
ConKruskalMST(&graph); // MST 변환
ShowGraphEdgeInfo(&graph);
ShowGraphEdgeWeightInfo(&graph);
GraphDestroy(&graph);
return 0;
}
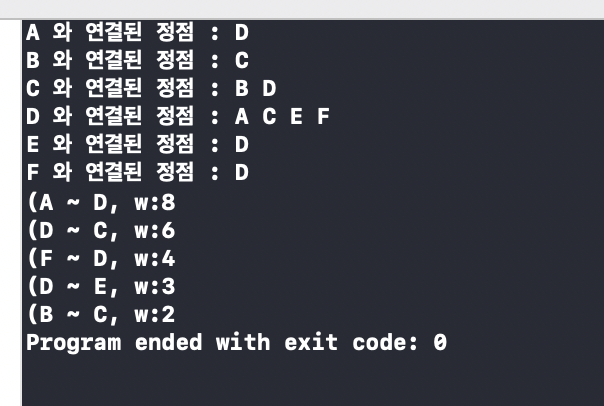
성공적이다.
자료구조 공부하느라 고생했다.
2021년 3월 12일 자료구조를 시작하여
2021년 4월 25일 최소 비용신장 까지 자료구조를 끝냈다.
이제 2-3회독의 복습을 추가로 진행할것인데!
바로는 안할것이다.
우선 C++을 진행하며
알고리즘문제를 풀며 종종 찾아올것이다.
수고했다.
찡긋! 😁
