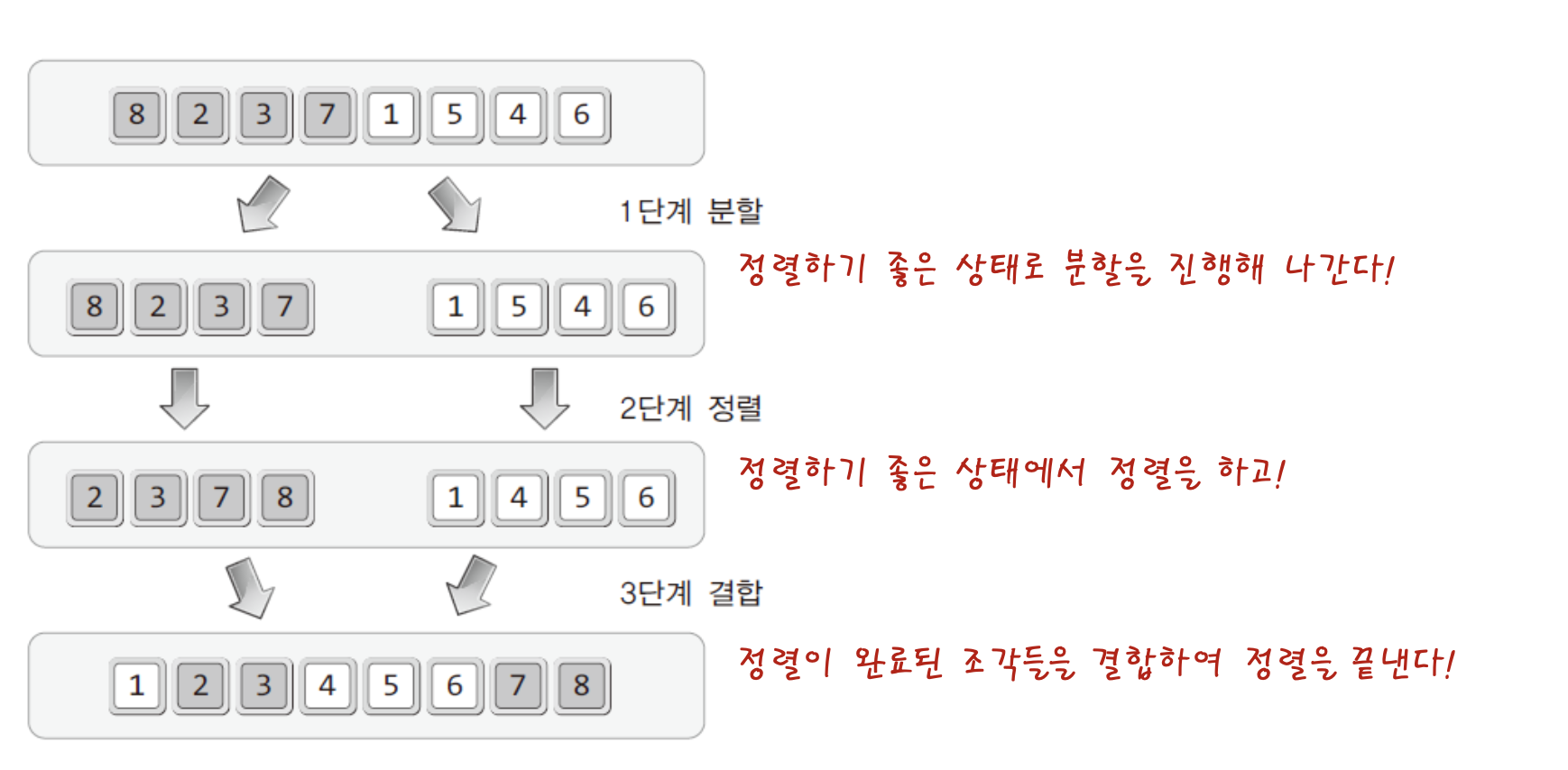
병합 정렬 : 이해와 구현
병합 정렬은 "분할 정복" 이라는 알고리즘 디자인 기법에 근거하여 만들어진 정렬 방법이다.
분할 정복이란, 말 그대로 복잡한 문제를 복잡하지 않은 문제로 분할하여! 정복! 하는 방법이다.
단!! 분할을 하고 정복까지 했으니 결합의 과정을 거쳐야 완성된다
- 1 단계 분할 : 해결이 용이한 단계까지 문제를 분할해나간다.
- 2 단계 정복 : 분할한 문제를 해결한다.
- 3 단계 결합 : 해결한 결과를 결합하여 마무리~!
그렇다면 어떻게 이 방법을 병합 정렬 알고리즘이 디자인됐을까!?
기본 원리는 이렇다!
"8개의 데이터를 동시에 정렬하는 것 보다! 이를 둘로 나눠서 4개의 데이터를 정렬 하는것이 쉽고, 또 이들 각각을 다시 한번 둘로 나눠서 2개의 데이터를 정렬하는 것이 더 쉽다! "
어떤가 8개의 데이터를 나눠서 결국 마지막 2개의 데이터만 남을때 까지 분할을 하면 if문을 써서 간단히 정렬할 수 있을것같지 않은가!
하지만...
이는 보기 좋게 틀렸다.
왜냐!
고정관념에 사로잡혀있기때문이다 !
왜 굳이 2개까지 남아야하느냐!
병합 정렬은 데이터가 1개만 남을 때까지 분할을 해나간다.
데이터가 2개만 남아도 정렬을 할 필요가 있지만, 1개만 남으면 그 조차 불필요 하기때문이다!!!!!
우옷...
고정관념을 깨뜨렸다! 두개가 있어야한다는!
언뜻 보면 나누는 것이 핵심인 것 같지만
실제 정렬은 나눈 것을 병합하는 과정에서 이뤄진다!!!!
그래서 병합 정렬이다.

보이는가! 병합해 나가면서 정렬하는것을!
사진에서 보이듯이
분할의 과정에서는
그저 전체 데이터를 둘로 나누는 과정을 데이터가 하나씩 구분이 될 때까지 진행하면된다!
즉 전체/2 를 계속한다는 말씀!
데이터가 8개이면
8->4->2->1 총 3번 진행한다.
이제 병합을 해보자 !
우선 나뉘었던 둘을 정렬 순서를 고려해서 묶는다.
이르케 분할이 3번된 만큼
병합도 3번진행한다 !
그럼 필자의 질문에 답을 해보자
"분할의 과정에서 하나씩 구분이 될 때까지 둘로 나누는 과정을 반복하는 이유는 무엇인가!? 처음부터 하나씩 구분을 해버리면 더 간단하지 않는가?!"
답은...! 내가 생각한답은!!! 그래야지 편하다..?
댕청 ㅎㅅㅎ
정답은 바로 !
"재귀적 구현을 위한 것"
키야... 그놈의 재귀..또 나왔다. 이 중 MergeTwoArea(arr,left,mid,right);
이 중 MergeTwoArea(arr,left,mid,right);
를 해석하면
배열 arr 의 left~mid, mid+1 ~ right까지 각각 정렬이 되어 있으니, 이를 하나의 정렬된 상태로 묶어서 배열 arr에 저장하라 !
이제 완성된 코드를 보자,,
#include <stdio.h>
#include <stdlib.h>
void MergeTwoArea(int arr[], int left, int mid, int right)
{
int fIdx =left;
int rIdx = mid + 1;
int i;
int * sortArr = (int*)malloc(sizeof(int)*(right+1));
int sIdx =left;
while(fIdx<=mid&&rIdx<=right)
{
if(arr[fIdx]<=arr[rIdx])
sortArr[sIdx] =arr[fIdx++];
else
sortArr[sIdx]= arr[rIdx++];
sIdx++;
}
if(fIdx > mid)
{
for(i=rIdx;i<=right;i++,sIdx++)
sortArr[sIdx]= arr[i];
}
else{
for(i=fIdx;i<=mid;i++,sIdx++)
sortArr[sIdx] = arr[i];
}
for(i=left; i<=right; i++)
arr[i] = sortArr[i];
free(sortArr);
}
void MergeSort(int arr[],int left,int right)
{
int mid;
if(left < right)
{
//중간 지점을 게산한다.
mid = (left+right)/2;
MergeSort(arr, left, mid);
MergeSort(arr, mid+1, right);
MergeTwoArea(arr, left, mid, right);
}
}
int main(void)
{
int arr[7]={3,2,4,1,7,6,5};
int i;
MergeSort(arr,0,sizeof(arr)/sizeof(int)-1);
for (i=0; i<7; i++) {
printf("%d ",arr[i]);
}
printf("\n");
return 0;
}
우왓..!
짱신기하지않는가.,, 신기할수록 큰일나는 법이다.
ㅠㅅㅠ 이제 함수들을 분석해보자..! 
void MergeTwoArea(int arr[], int left, int mid, int right)
{
int fIdx =left;
int rIdx = mid + 1;
int i;
// 병합 한 결과를 담을 배열 sortArr의 동적 할당!
int * sortArr = (int*)malloc(sizeof(int)*(right+1));
int sIdx =left;
while(fIdx<=mid&&rIdx<=right)
{
// 병합 할 두 영역의 데이터를 비교하여, 정렬 순서대로 sortArr에 하나씩 옮겨 담는다.
if(arr[fIdx]<=arr[rIdx])
sortArr[sIdx] =arr[fIdx++];
else
sortArr[sIdx]= arr[rIdx++];
sIdx++;
}
if(fIdx > mid) // 배열의 앞부분이 모두 SortArr에 옮겨 졌다면
{
//배열 뒷부분에 남은 데이터들을 모두 sortArr에 그대로 옮긴다.
for(i=rIdx;i<=right;i++,sIdx++)
sortArr[sIdx]= arr[i];
}
else{ // 배열의 뒷부분이 모두 옮겨졌다면
for(i=fIdx;i<=mid;i++,sIdx++) //배열의 앞부분에 남은 데이터들을 그대로 옮긴다.
sortArr[sIdx] = arr[i];
}
for(i=left; i<=right; i++)
arr[i] = sortArr[i];
free(sortArr);
}먼저 while문의 반복조건을 이해하는것이 중요하다.
while(fIdx<=mid&&rIdx<=right)
{
// 병합 할 두 영역의 데이터를 비교하여, 정렬 순서대로 sortArr에 하나씩 옮겨 담는다.
if(arr[fIdx]<=arr[rIdx])
sortArr[sIdx] =arr[fIdx++];
else
sortArr[sIdx]= arr[rIdx++];
sIdx++;
}fidx, ridx에는 각각 병합할 두 영역의 첫 번째 위치정보가 담긴다.
그리고 이 두 변수의 값을 증가시켜 가면서
두 영역의 데이터들을 비교해 나가게 된다.
그런데 ! 병합할 두 영역이라는 것이 하나의 배열 안에 함께 존재한다.
따라서 !
fIdx는 배열의 앞족 영역을 가리키고, rIdx는 배열의 뒤쪽 영역을 가리키게 되는데..배열의 앞과 뒤 구분은 mid에 저장되어 있다.
mid+1 위치서부터 뒤쪽 영역이 시작되기 때문이다!
이를 그림으로 한번 보자 !
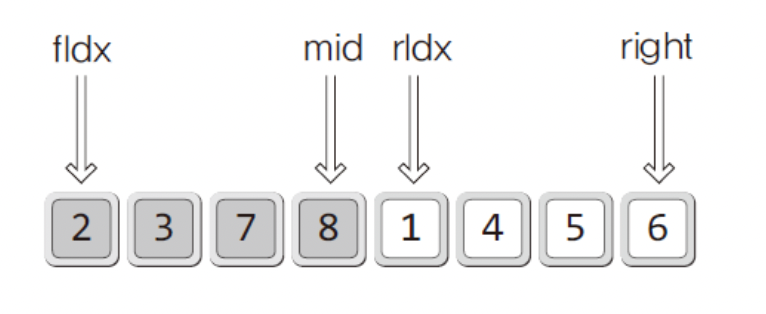
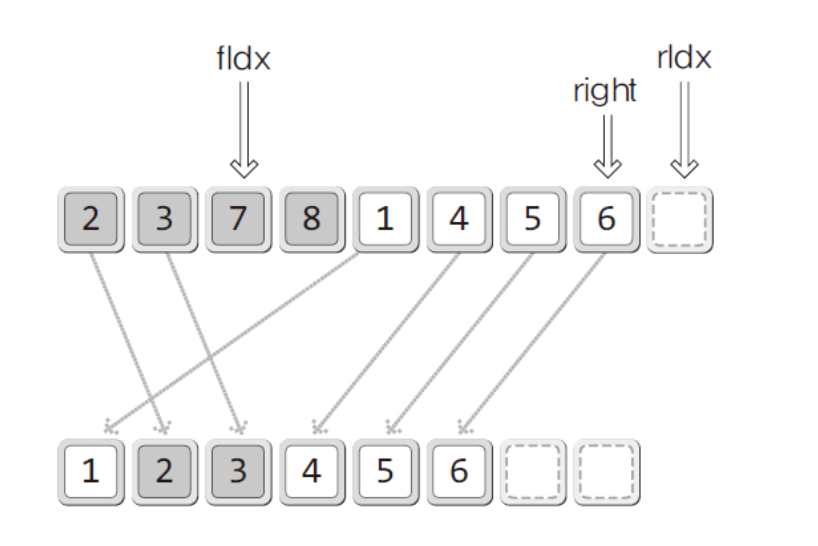
이 그림은 두 영역을 합치기 직전의 상태를 보여준다.
fIdx,rIdx가 가리키는 위치에 주목하자!
이 둘에 저장된 값은 하나씩 증가하면서 다음과 같이 값의 비교를 진행한다.
- 2 와 1 비교 : 1을 sortArr로 이동, rIdx 1증가
- 2 와 4 비교 : 2을 sortArr로 이동, fIdx 1증가
- 3 와 4 비교 : 3을 sortArr로 이동, fIdx 1증가
- 7 와 4 비교 : 4을 sortArr로 이동, rIdx 1증가
- 7 와 5 비교 : 5을 sortArr로 이동, rIdx 1증가
- 7 와 6 비교 : 6을 sortArr로 이동, rIdx 1증가
이러한 과정을 거치고 나면 rIdx 의 값이 right보다 커지게 되어 반복문을 탈출하게된다.
이는! 배열의 뒤쪽 영역이 모두 옮겨졌다는 것을 의미하며
이와 반대로 fIdx 가 mid 보다 커지는 경우는 배열의 앞쪽 영역이 모두 옮겨졌다는 것이다!
자 ! 그럼 이제 while문의 반복 조건이 의미하는 바를 알겠는가!?
이는 바로 배열의 앞쪽 영역에도, 뒤쪽 영역에도 비교의 대상이 남아있는 상황에서 반복조건이 "참"임을 의미한다.
그렇다면!이제 위의 반복영역을 탈출한 후 어느 영역에 데이터가 남아 있는지 확인하여
이를 그대로~ 옮기면 그만이다!!
그래서 그 다음 if else 문이 등장하여 앞이 다 들어갔는지~ 뒤가 다 들어갔는지 체크 후 남은 부분을 넣어준당~!
병합 정렬 : 성능 평가
성능평가를 위해서 비교,이동 연산의 횟수를 계산 해봐야하는데 MergeSort 함수가 아닌 MergeTwoArea 함수를 기준으로 계산해야한다.
비교연산과 이동연산이 실제 정렬을 진행하는 MergeTwoArea 함수를 중심으로 진행되기 때문이다.
자 ! 다시 반복문을 보자..
while(fIdx<=mid&&rIdx<=right)
{
// 병합 할 두 영역의 데이터를 비교하여, 정렬 순서대로 sortArr에 하나씩 옮겨 담는다.
if(arr[fIdx]<=arr[rIdx])//핵심연산
sortArr[sIdx] =arr[fIdx++];
else
sortArr[sIdx]= arr[rIdx++];
sIdx++;
}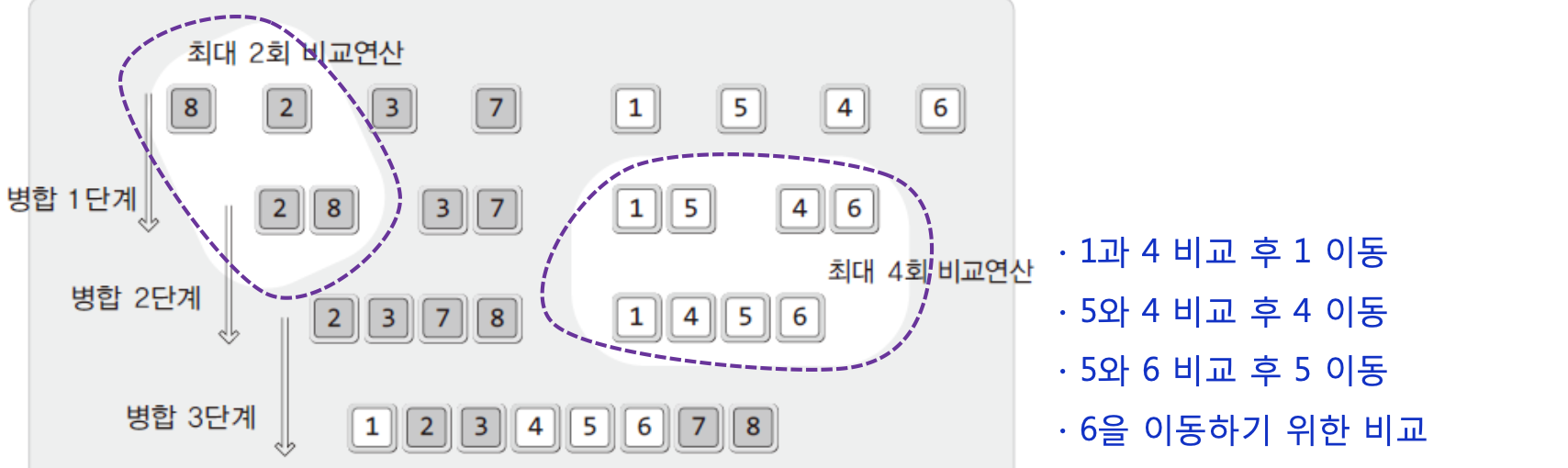
사진에서 보이듯 8과 2가 모여 둘이 될때 최대 2회 진행이 된다!
그런데 8과2를 뭉치는데 왜 비교연산 횟수가 1이 아니고 2냐!?
바로!!
while문 이후에 등장하는 if~else 때문에 한개 더 더해 2라고한다 !
그렇다면 1단계에서는 총 8회 생기게된다.
그렇담.. 둘과 둘이 모여 넷이 될때는!?
- 1과 4비교
5와 4 비교
5와 6비교
6 if else문 비교
4번이다!
그렇담 총 비교연산횟수는 8 회이다!!
이제 어느정도 이러한 규칙이 보이지 않는가!?
정렬의 대상인 데이터의 수가 n개 일 떄, 각 병합의 단계마다 최대 n번의 비교연산이 진행된다.
따라서!
최대 비교연산의 횟수는 다음과 같다
n*log(2)N
따라서 빅오도 위에랑같당
이제 이동연산에 대해 알아보자 .
while(fIdx<=mid&&rIdx<=right)
{
// 병합 할 두 영역의 데이터를 비교하여, 정렬 순서대로 sortArr에 하나씩 옮겨 담는다. // 이동 !
if(arr[fIdx]<=arr[rIdx])
sortArr[sIdx] =arr[fIdx++]; //이동!
else
sortArr[sIdx]= arr[rIdx++]; // 이동!
sIdx++;
}
///
for(i=left; i<=right; i++)
arr[i] = sortArr[i]; //임시배열에 있는거 원래 배열로 이동!
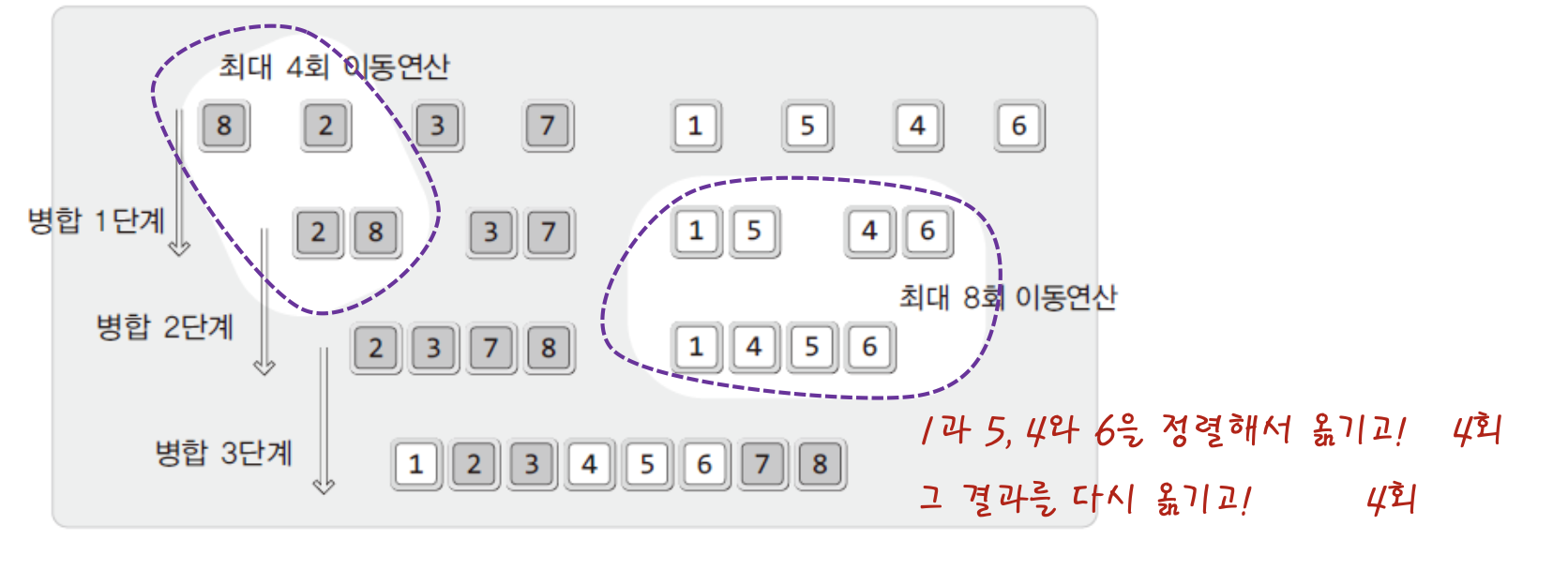
- 임시 배열에 데이터를 병합하는 과정에서 한 번!
- 임시 배열에 저장된 데이터를 전부를 원위치로 옮기는 과정에서 한 번 !
따라서 비교연산의 두 배에 해당하는 이동연산이 이뤄진다! 
두배이지만! 빅오는 뭐냐!
숫자를 무시한다구!!!
그러므로 이동이나 비교연산의 빅오는 동일하다는것을 알 수 있다.
참고로 병합정렬에는 임시 메모리가 필요하다는 단점이 있다.
하지만 이는 정렬의 대상이 배열이 아닌 연결 리스트일 경우 단점이 되지 않기 때문에!
연결 리스트의 경우에는 병합정렬에서 그 만큼 더 좋은 성능을 기대할 수 있다!!!
그렇다면 이제 내가 할것은 뭐냐..
바로 연결리스트에서의 병합정렬을 생각해보는 것이다!
차분히 생각해보자 !!!