앞서 소개한 단순한 정렬 알고리즘은 정렬대상의 수가 적은 경우 효울적으로 사용할 수 있지만 정렬 대상의 수가 적지 않은 경우에는 아니다!
그러므로 우리는 이 경우에서도의 만족스러운 결과를 보장하는 알고리즘이 필요하다.
✏️힙 정렬 : 이해와 구현
제목만 복잡하지만..이지! 사실상 앞서 설명한 정렬들이 너무 ~ 간단해서 그에 비해 상대적으로 복잡한 알고리즘이라는뜻이므로 겁먹지 말라는뎅..오히려 기발한 정렬방식이라 나름 재밌을것같다는데....
모르겠다!😂
우선 힙 정렬에 대해 배워보자 !!
힙을 잘 이해했다면 별도로 더 공부할 것이 없는 알고리즘이다.
"힙의 루트 노드에 저장된 값이 가장 커야 한다."
이는 최대 힙의 특징이므로
"힙의 루트 노드에 저장된 값이 정렬순서상 가장 앞선다"라고 말할수 있다.
그럼 다음 예제(소스코드)를 보자
#include <stdio.h>
#include "UsefulHeap.h"
int PriComp(int n1,int n2)
{
return n2-n1; // 오름차순 정렬을 위한 문장.
}
void HeapSort(int arr[],int n,PriorityComp pc)
{
Heap heap;
int i;
HeapInit(&heap,pc);
//정렬 대상을 가지고 힙을 구성한다.
for(i=0;i<n;i++)
{
HInsert(&heap, arr[i]);
}
//순서대로 하나씩 꺼내서 정렬을 완성한다.
for(i=0;i<n;i++)
{
arr[i] = HDelete(&heap);
}
}
int main(void){
int arr[4] = {3,4,2,1};
int i;
HeapSort(arr, sizeof(arr)/sizeof(int), PriComp);
for(i=0;i<4;i++)
{
printf("%d ",arr[i]);
}
printf("\n");
return 0;
}
추가 파일 : UsefulHeap.c,h
힙을 써야하니 당연빠따로 앞서 구현한 유용한 힙의 헤더와 소스파일을 가져왔다.
결과 정렬이 완료된것을 볼 수 있다.
그럼 예제를 분석해보자.
for(i=0;i<n;i++)
{
HInsert(&heap, arr[i]);
}데이터를 모두 힙에 넣는다.
for(i=0;i<n;i++)
{
arr[i] = HDelete(&heap);
}힙에서 다시 데이터를 꺼낸다.
보다시피.. 정렬의 대상인 데이터들을 그저 힙에 넣었다가 꺼내는 것이 전부이다.
그럼에도 불구하고 정렬이 완성되는 이유는
꺼낼 때 힙의 루트 노드에 저장된 데이터가 반환되기 때문이다 !!! !
힙 정렬 : 성능 평가
언뜻보면 그저 데이터를 전부 넣고 빼서 성능상 이점이 없어 보이지만, 지금까지 소개한 것 중에서는 킹왕짱이다.
힙의 데이터 저장/삭제 시간 복잡도는 로그이엔 이라고 앞서 계산했었다.
따라서 삽입과 삭제를 하나의 연산으로 묶는다면,
정렬대상의 수가 n개라면, 총 n개의 데이터를 삽입 및 삭제 해야하므로 n을 곱해야한다.
그러므로
엔곱하기 로그이엔 이다!
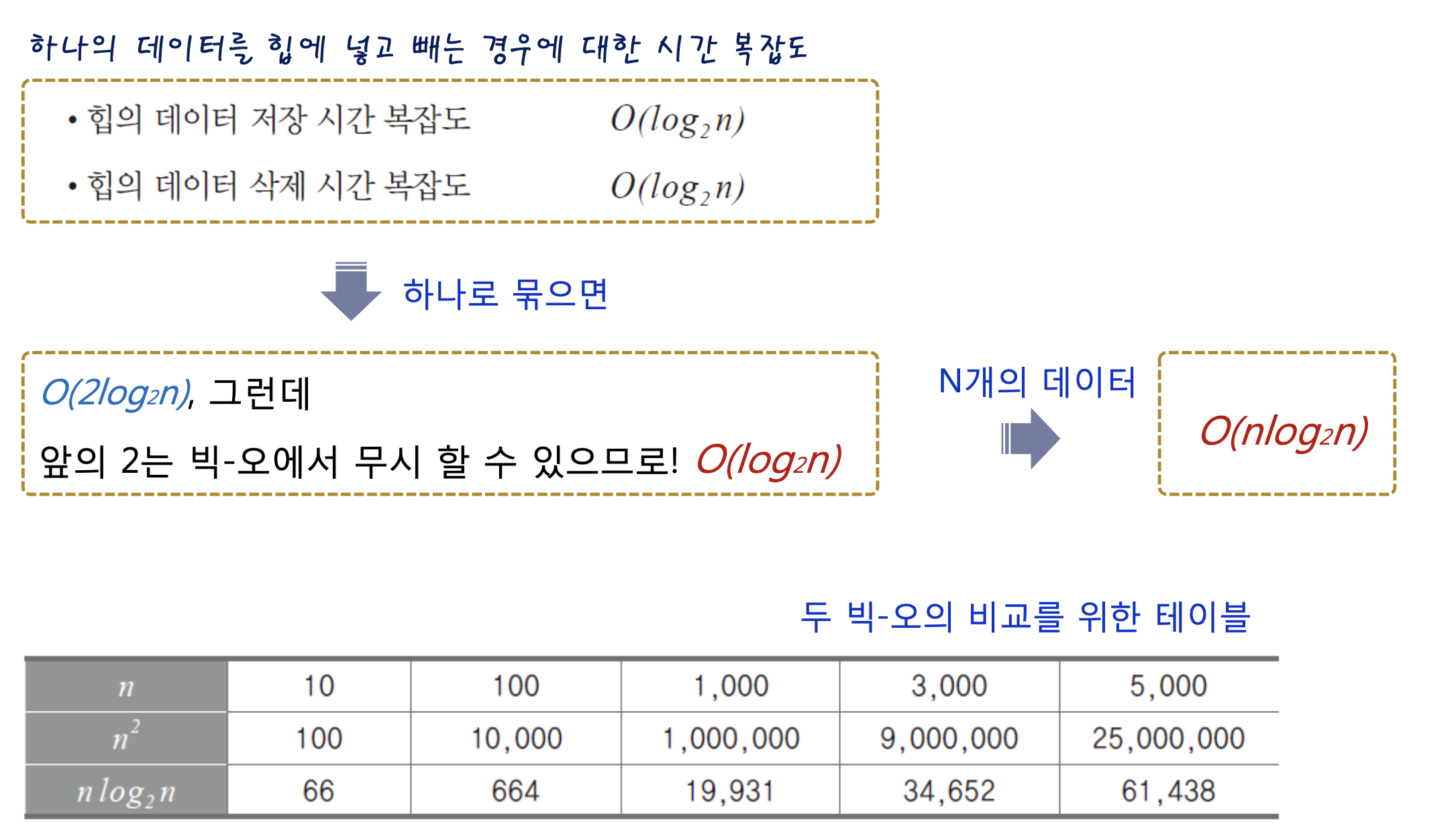
n제곱과 엔곱하기 로그이엔은 큰 차이가 있다 !!!
