[자료구조] 이진 트리의 순회 8-3

순회의 세 가지 방법

• 전위 순회 : 루트 노드를 먼저 !
  
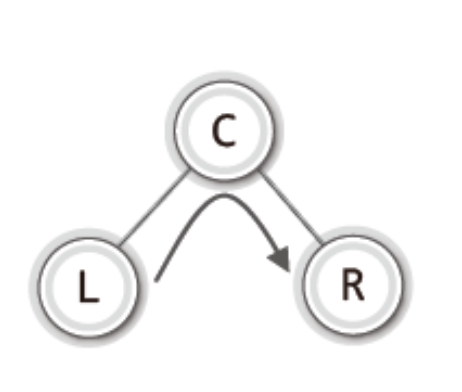
• 중위 순회 : 루트 노드를 중간에 !

• 후위 순회 : 루트 노드를 마지막에 !

이렇듯 이진트리를 순회하는 방법에는 "루트 노드를 언제 방문하느냐" 에 따라서 나뉜다.

이렇게 높이가 1인 트리의 순회는 어렵지 않는데..
그 이상의 높이를 가진 트리는 어떻게 순회를 하는가에 대해 의문이 생길 수 있다.

그 의문의 해결은 바로 재귀에 있다.
이진 트리는 그 구조가 재귀적이기 때문에 위의 세 가지 순회방법을 재귀적으로 구현만 하면 문제는 해결된다.

순회의 재귀적 표현

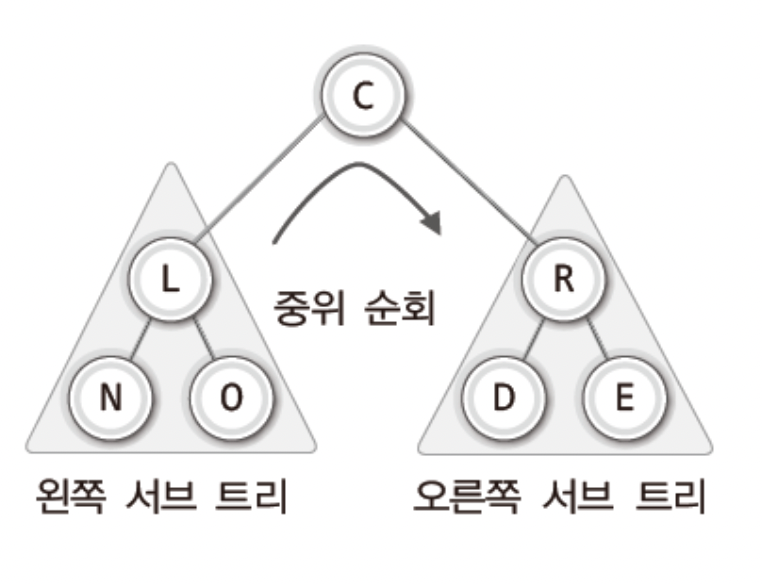
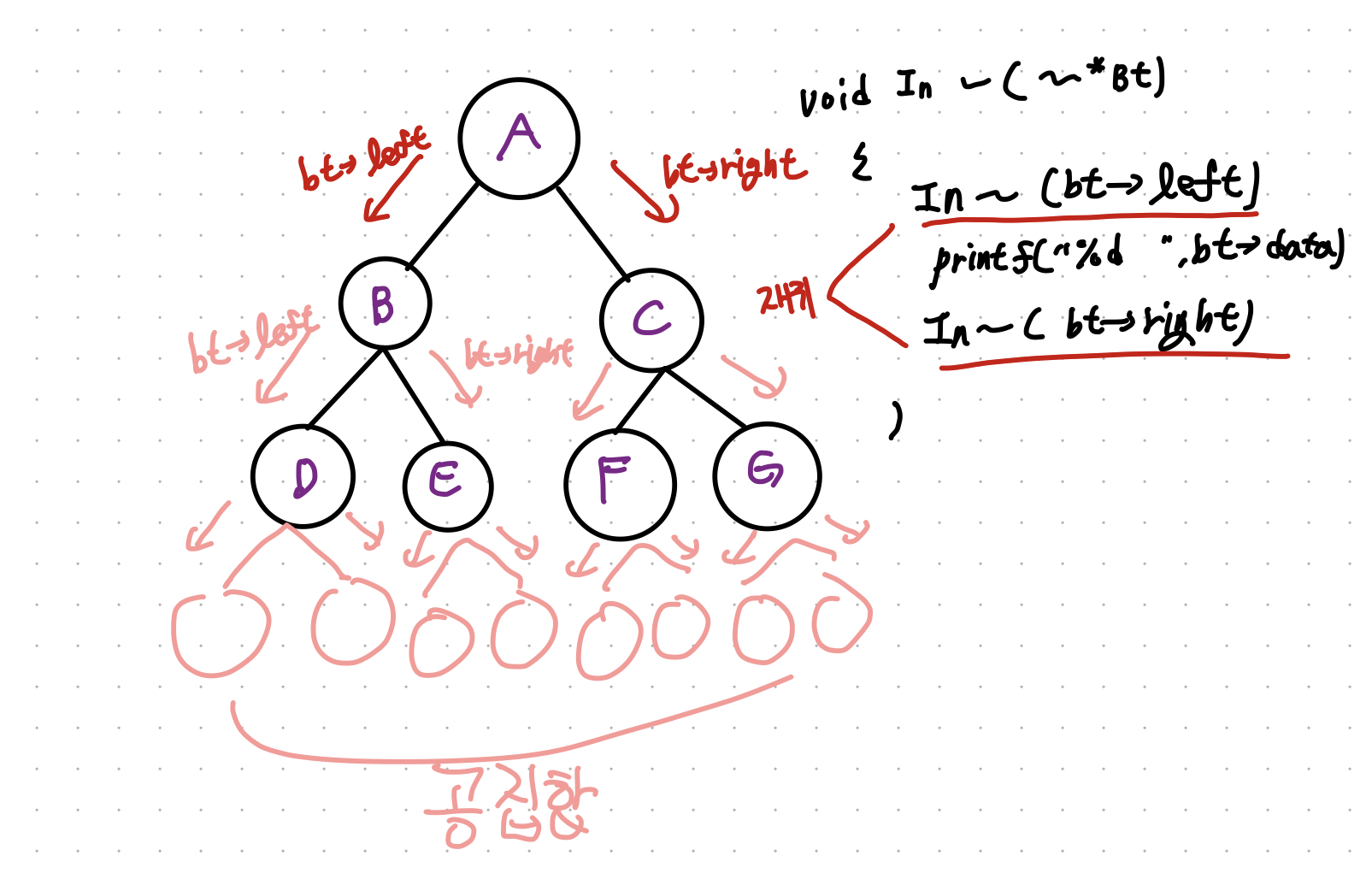
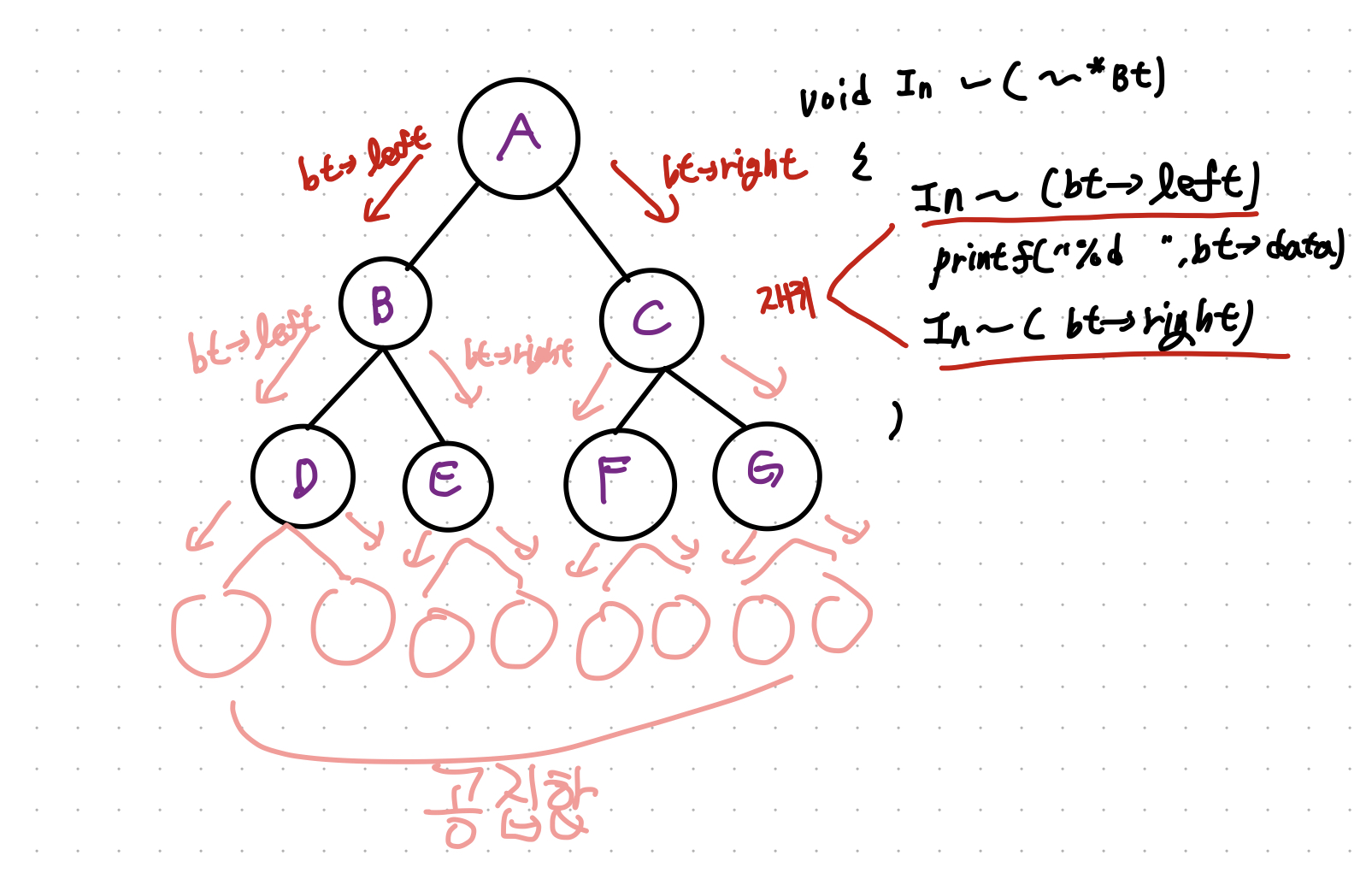
위 그림의 이진 트리를 대상으로 중위 순회 할 경우

1. 왼쪽 서브 트리의 순회
2. 루트 노드의 방문
3. 오른쪽 서브 트리의 순회

서브트리라고 해서 순회의 방법이 달라지는 것은 아니다.
이들도 중위순회를 진행 하면된다!

따라서 이진 트리 전체를 순회하는 함수는 일단 이렇게 정의 할 수 있다.

void InorderTraverse(BTreeNode * bt)
{
    InorderTraverse(bt -> left); // 왼쪽 서브트리 순회
    printf("%d \n",bt->data); // 루트 노드 방문
    InorderTraverse(bt -> right); // 오른쪽 서브트리 순회
}

어떤가 매우 재귀적이지 않은가 ! 이를 토대로 내가 이해한 그림을 보이겠다.
ㅋㅋㅋ... 매우 난잡
bt->left 가 재귀를 돌면서 자신이 루트노드가 되고 그 이후 left,right도 재귀로 자신이 루트노드가 되고.. 이런식으로 쭈우우욱 간다.. 그런데 언제 탈출하지..? 공집합을 가리킬때는 NULL 을 가지니 이때 탈출하면 될거같기도...?

하지만 ~ !
이 함수에서도 두 가지 의문을 재기 할 수 있다.

• 재귀의 탈출 조건이 정의되어 있지 않다!
• 노드의 방문이 그저 데이터의 출력이냐?

첫번째 질문은 나의 예상이 적중했다!
그리고 두번째 질문은 순회의 방법에 초점을 둔것이니 현재로서는 무시해도 상관없다.
이를 통해 탈출까지 합친 코드는 !

void InorderTraverse(BTreeNode * bt)
{
    if(bt ==NULL) 
    	return; // 탈출 ~! 
    InorderTraverse(bt -> left); // 왼쪽 서브트리 순회
    printf("%d \n",bt->data); // 루트 노드 방문
    InorderTraverse(bt -> right); // 오른쪽 서브트리 순회
}

이로써 중위 순회 함수 완성!
main.c 에 이 함수를 추가하고 결과를 보자 !

//
//  main.c
//  BinaryTree


#include <stdio.h>
#include "BinaryTree.h"

void InorderTraverse(BTreeNode * bt)
{
    if(bt ==NULL)
        return; // 탈출 ~!
    
    InorderTraverse(bt -> left); // 왼쪽 서브트리 순회
    printf("%d \n",bt->data); // 루트 노드 방문
    InorderTraverse(bt -> right); // 오른쪽 서브트리 순회
}

int main(void)
{
    BTreeNode * bt1 = MakeBTreeNode(); // 노드 1 생성
    BTreeNode * bt2 = MakeBTreeNode(); // 노드 2 생성
    BTreeNode * bt3 = MakeBTreeNode(); // 노드 3 생성
    BTreeNode * bt4 = MakeBTreeNode(); // 노드 4 생성
    
    SetData(bt1, 1); //bt1 에 1 저장
    SetData(bt2, 2); //bt2 에 2 저장
    SetData(bt3, 3); //bt3 에 3 저장
    SetData(bt4, 4); //bt4 에 4 저장
    
    MakeLeftSubTree(bt1, bt2); // bt2를 bt1의 왼쪽 자식 노드로
    MakeRightSubTree(bt1, bt3); // bt3를 bt1의 오른쪽 자식 노드로
    MakeLeftSubTree(bt2, bt4); // bt4를 bt2의 왼쪽 자식 노드로
    
    InorderTraverse(bt1);
    
    return 0;
}

돌리기전에 미리 예상해보자.

bt->left 의 재귀가 끝나고 나서야 루트노드가 출력 될것이니 4->2->1 일것이다.
이후 bt->right를 타면 3뿐이다 !
그러므로 4->2->1->3 !

돌려보자 !

크하핳! 맞다 !
그런데.. 이제 중위 했다.
남은것은 후위 전위 인데...
하!! 언제 다 생각하냐!! 생각들겠지만 생각보다 쉽다.
아까 말하지 않았는가 !

노드를 방문하는 순서의 차이.

그렇다!
그렇다면 전위는 루트부터 후위는 루트를 마지막!
이를토대로 후위/전위 순회 코드를 보여주겠다

void PreorderTraverse(BTreeNode * bt) //전위 함수
{
    if(bt ==NULL)
        return; // 탈출 ~!
    
    printf("%d \n",bt->data); // 루트 노드 방문
    InorderTraverse(bt -> left); // 왼쪽 서브트리 순회 
    InorderTraverse(bt -> right); // 오른쪽 서브트리 순회
}

void PostorderTraverse(BTreeNode * bt)
{
    if(bt ==NULL)
        return; // 탈출 ~!
    
    InorderTraverse(bt -> left); // 왼쪽 서브트리 순회 
    InorderTraverse(bt -> right); // 오른쪽 서브트리 순회
    printf("%d \n",bt->data); // 루트 노드 방문
}

쉽지않은가!!!

노드의 방문이유

노드의 방문이유는 안타깝게도.. 출력이 전부가 아니다.
방문의 목적은 상황에 따라 달라진다.
따라서 방문했을 때 할 일을 결정하도록 "함수 포인터"를 사용하면된다.

먼저 중위 부터 변경해보겠다.

typedef void (*VisitFuncPtr)(BTData data);

void InorderTraverse(BTreeNode * bt,VisitFuncPtr action)
{
    if(bt ==NULL)
        return; // 탈출 ~!
    
    InorderTraverse(bt -> left, action); // 왼쪽 서브트리 순회
   action(bt->data); // 루트 노드 방문
    InorderTraverse(bt -> right, action); // 오른쪽 서브트리 순회
}

함수의 주소값을 매개변수action을 통해 전달받도록 변경하였다.

즉 매개변수 action에 전달되는 함수의 내용에 따라서 노드의 방문결과가 졀정된다.

이를 통해서 각 노드들을 출력하는 프로그램을 만들어보자
BinaryTree2.h

//
//  BinaryTree.h
//  BinaryTree

#ifndef BinaryTree_h
#define BinaryTree_h

typedef int BTData;

typedef struct _bTreeNode // 이진 트리의 노드를 표현한 구조체이다.
{
    BTData data; // 가지고 있는 데이터
    struct _bTreeNode * left; // 왼쪽 빈칸
    struct _bTreeNode * right; // 오른쪽 빈칸
} BTreeNode; // 타입뎊!

BTreeNode * MakeBTreeNode(void); // 노드의 생성
BTData GetData(BTreeNode * bt); // 노드에 저장된 데이터 반환
void SetData(BTreeNode * bt, BTData data); // 노드에 데이터 저장

BTreeNode * GetLeftSubTree(BTreeNode * bt); // 왼쪽 서브 트리 주소 값 반환
BTreeNode * GetRightSubTree(BTreeNode * bt); // 오른쪽 서브 트리 주소 값 반환

void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub); //Main노드가 왼쪽 자식 노드로 sub노드 연결
void MakeRightSubTree(BTreeNode * main, BTreeNode * sub); //Main노드가 오른쪽 자식 노드로 sub노드 연결

typedef void (VisitFuncPtr)(BTData data); // 포인터 함수 

void PreorderTraverse(BTreeNode * bt, VisitFuncPtr action);
void InorderTraverse(BTreeNode * bt, VisitFuncPtr action);
void PostorderTraverse(BTreeNode * bt, VisitFuncPtr action);


#endif /* BinaryTree_h */

기존 파일에 전위,중위,후위를 추가해줬다.

BinaryTree.c

//
//  BinaryTree.c
//  BinaryTree
//
//
#include <stdio.h>
#include <stdlib.h>
#include "BinaryTree.h"

BTreeNode * MakeBTreeNode(void)
{
    BTreeNode * nd = (BTreeNode *)malloc(sizeof(BTreeNode)); //nd 노드 동적할당
    nd->left = NULL;
    nd ->right = NULL; //왼쪽 오른쪽 Null 가리키게한다.
    return nd;
}

BTData GetData(BTreeNode * bt)
{
    return bt->data; //bt에 저장된 data 값을 반환해서 보여준다
}

void SetData(BTreeNode * bt, BTData data)
{
    bt->data = data; //bt의 data값을 전달받은 data로 넣는다.
}

BTreeNode * GetLeftSubTree(BTreeNode * bt)
{
    return bt->left; // 왼쪽 서브 트리 주소 값 반환
}

BTreeNode * GetRighttSubTree(BTreeNode * bt)
{
    return bt->right;
}

void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub)
{
    if(main->left != NULL)
        free(main->left); // 만약 main의 left가 이미 차져있다면 그 쪽 데이터를 지운다 !
    
    main->left = sub; // sub로 넣는다 !
}

void MakeRightSubTree(BTreeNode * main, BTreeNode * sub)
{
    if(main->right != NULL)
        free(main->right); // 만약 main의 left가 이미 차져있다면 그 쪽 데이터를 지운다 !
    
    main->right = sub; // sub로 넣는다 !
}

void PreorderTraverse(BTreeNode * bt, VisitFuncPtr action) //전위 함수
{
    if(bt ==NULL)
        return; // 탈출 ~!
    
    action(bt->data); // 루트 노드 방문
    InorderTraverse(bt -> left,action); // 왼쪽 서브트리 순회
    InorderTraverse(bt -> right, action); // 오른쪽 서브트리 순회
}

void PostorderTraverse(BTreeNode * bt, VisitFuncPtr action)
{
    if(bt ==NULL)
        return; // 탈출 ~!
    
    InorderTraverse(bt -> left, action); // 왼쪽 서브트리 순회
    InorderTraverse(bt -> right, action); // 오른쪽 서브트리 순회
    action(bt->data); // 루트 노드 방문
}

void InorderTraverse(BTreeNode * bt,VisitFuncPtr action)
{
    if(bt ==NULL)
        return; // 탈출 ~!
    
    InorderTraverse(bt -> left, action); // 왼쪽 서브트리 순회
    action(bt->data); // 루트 노드 방문
    InorderTraverse(bt -> right, action); // 오른쪽 서브트리 순회
}

기존 파일에 함수들의 내용들을 적어줬다.

main.c

//
//  main.c
//  BinaryTree
//


#include <stdio.h>
#include "BinaryTree.h"

void ShowIntData(int data);

int main(void)
{
    BTreeNode * bt1 = MakeBTreeNode(); // 노드 1 생성
    BTreeNode * bt2 = MakeBTreeNode(); // 노드 2 생성
    BTreeNode * bt3 = MakeBTreeNode(); // 노드 3 생성
    BTreeNode * bt4 = MakeBTreeNode(); // 노드 4 생성
    BTreeNode * bt5 = MakeBTreeNode(); // 노드 5 생성
    BTreeNode * bt6 = MakeBTreeNode(); // 노드 6 생성

    
    
    SetData(bt1, 1); //bt1 에 1 저장
    SetData(bt2, 2); //bt2 에 2 저장
    SetData(bt3, 3); //bt3 에 3 저장
    SetData(bt4, 4); //bt4 에 4 저장
    SetData(bt5, 5); //bt4 에 5 저장
    SetData(bt6, 6); //bt4 에 6 저장
    
    MakeLeftSubTree(bt1, bt2); // bt2를 bt1의 왼쪽 자식 노드로
    MakeRightSubTree(bt1, bt3); // bt3를 bt1의 오른쪽 자식 노드로
    MakeLeftSubTree(bt2, bt4); // bt4를 bt2의 왼쪽 자식 노드로
    MakeRightSubTree(bt2, bt5); // bt5를 bt2의 오른쪽 자식 노드로
    MakeRightSubTree(bt3, bt6);
    
    PreorderTraverse(bt1, ShowIntData);
    printf("\n");
    InorderTraverse(bt1, ShowIntData);
    printf("\n");
    PostorderTraverse(bt1, ShowIntData);
    printf("\n");
    return 0;
}

void ShowIntData(int data)
{
    printf("%d ", data);
}

이를 통해 출력해주면

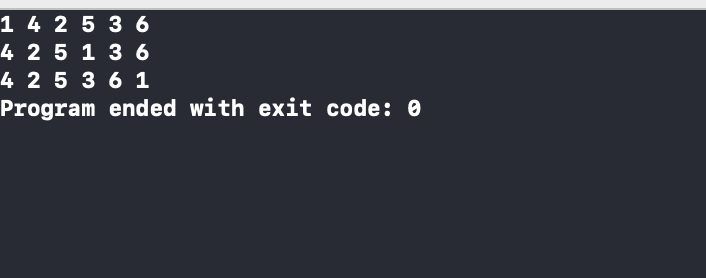
이렇게 뜨면 성공!!!