이진 트리에 대한 설명에 이어서
이제는 이진 트리의 일종인 수식 트리에 대해 배워보자.
앞에서는 이진 트리를 구성하는데 필요한 도구에 대해 만들었다면 이제는 이 도구를 이용하여 이진 트리의 일종인 "수식 트리"를 만들 것이다.
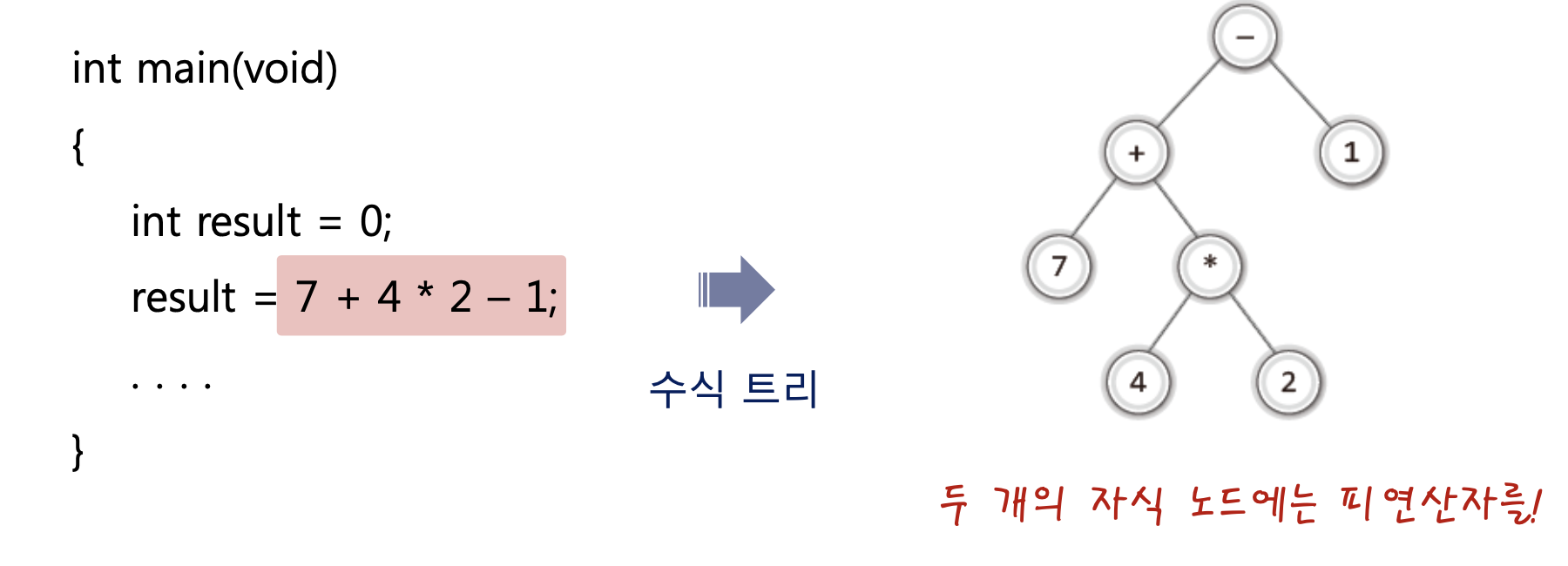
이러한 방식으로 중위 표기법 수식을 컴퓨터가 알아듣기 좋게 수식트리로 만드는 프로그램의 작성이 우리의 목적이다!
수식 트리는 중위 표기법? 후위 표기법?
아니다!
JUST 수식트리다.
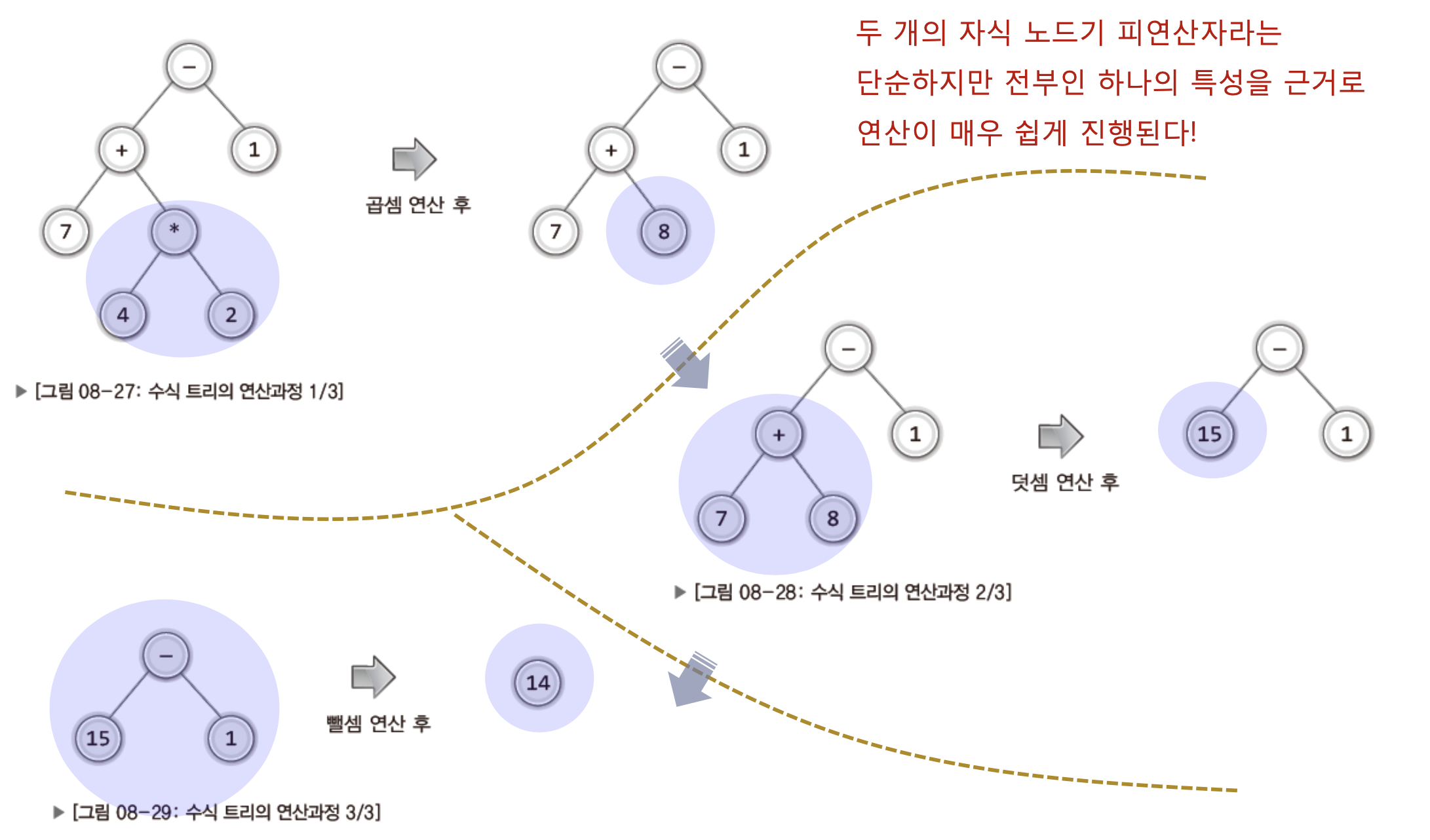
수식 트리를 구성하는 모든 서브 트리는 기본적으로 다음의 방식으로 연산이 진행된다.
"루트 노드에 저장된 연산자의 연산을 하되, 두 개의 자식 노드에 저장된 두 피연산자를 대상으로 연산을 한다."
이런식으로 !
그렇다면 이제 우리가 할 일은
1. 수식트리를 만든다.
2. 이 수식트리를 대상으로 연산을 진행하는 함수를 만든다.
이다 !
BUT ! 중위 표기법의 수식을 수식트리로 변환하는것은 매우 복잡하다!
그렇지만 ! 후위 표기법의 수식을 수식 트리로 표현하는 것은 비교적 간단하다.
그렇기에 우리는
중위 표기법 수식 -> 후위 표기법 수식 -> 수식 트리
이 과정을 거쳐야한다 !
수식 트리의 구현에 필요한 도구와 헤더파일 정의
수식트리도 이진 트리이다.
그렇기에 ! 이미 만들어놓은 것들을 활용하면 된다!
도구를 만들어놓고 활용하지않는것은 우매한 행동이다 !!
그리고 수식 트리를 만드는 과정에서 스택을 필요로 하다,
이것도 만들어 놓았으니 활용하자!
수식 트리 구현에 필요한 이진 트리 : BinaryTree2.h,c
수식 트리 구현에 필요한 스택 : ListBaseStack.h,c
우선 헤더파일을 보자
ExpressTree.h
//
// ExpressionTree.h
// ExpressionTree
#ifndef ExpressionTree_h
#define ExpressionTree_h
#include "BinaryTree2.h"
BTreeNode * MakeExpTree(char exp[]); // 수식 트리 구성
int EvaluateExpTree(BTreeNode * bt); // 수식 트리 계산
void ShowPrefixTypeExp(BTreeNode * bt); //전위 표기법 기반 출력
void ShowInfixTypeExp(BTreeNode * bt); //중위 표기법 기반 출력
void ShowPostfixTypeExp(BTreeNode * bt); //후위 표기법 기반 출력
#endif /* ExpressionTree_h */BTreeNode * MakeExpTree(char exp[]); // 수식 트리 구성이 함수는 후위 표기법 수식을 문자열로 받아서 이를 기반으로 수식 트리를 구성하여 수식 트리의 루트 노드의 주소 값을 반환하는 함수이다.
후위 표기법의 수식을 기반으로 수식 트리 작성하기.
우선 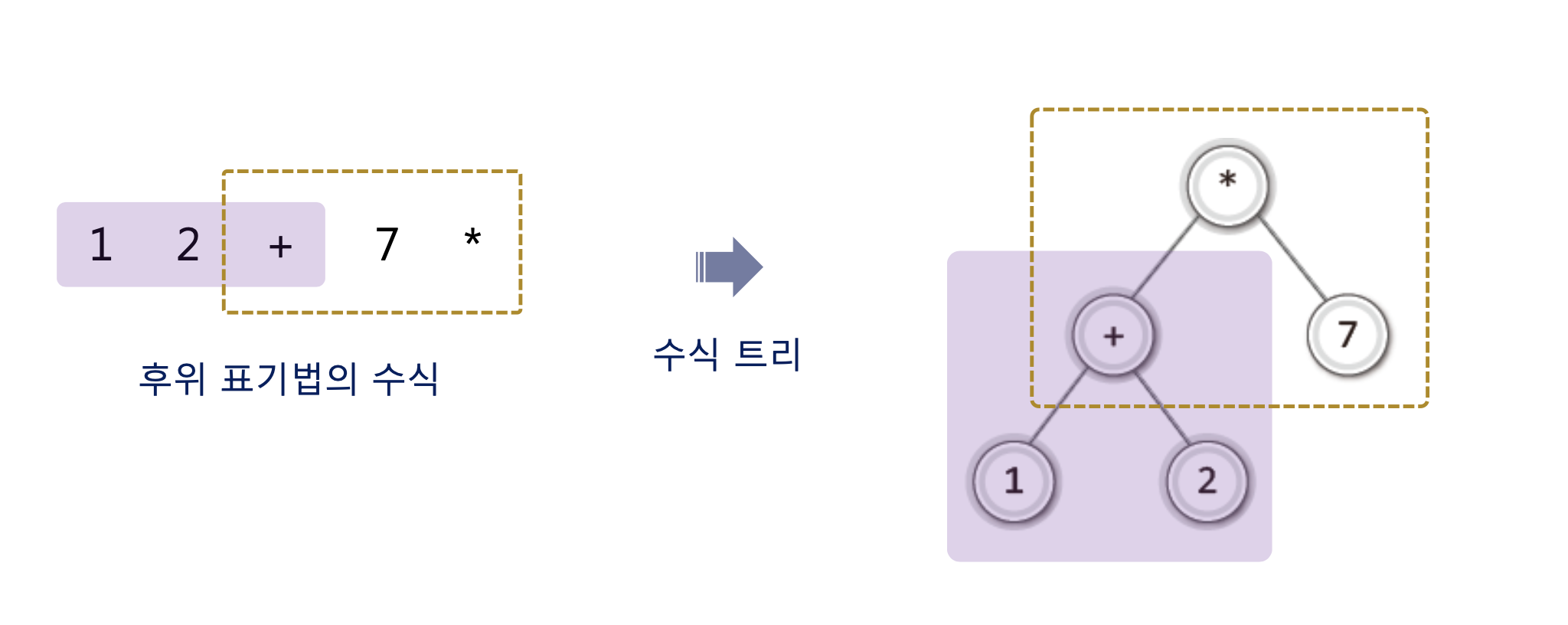
이를 보고 후위 표기법의 수식을 수식 트리로 변환하는 방법을 생각해보자 .
-> "후위 표기법의 수식에서 앞쪽에 등장하는 피연산자와 연산자를 이용해서 트리의 하단을 만들고, 이를 바탕으로 점진적으로 수식 트리의 윗부분을 구성해 나간다."
수식트리의 구성을 살펴보자.
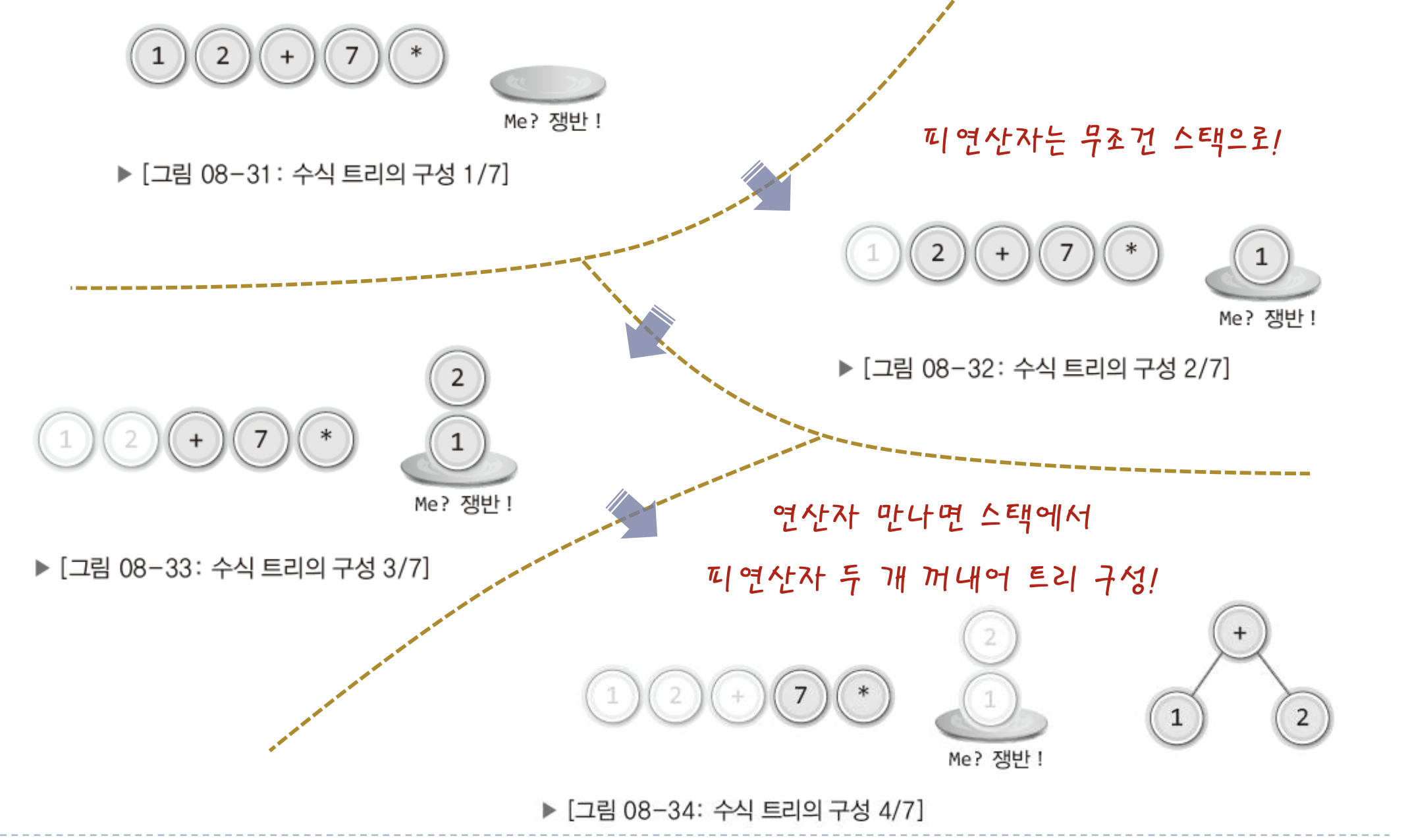
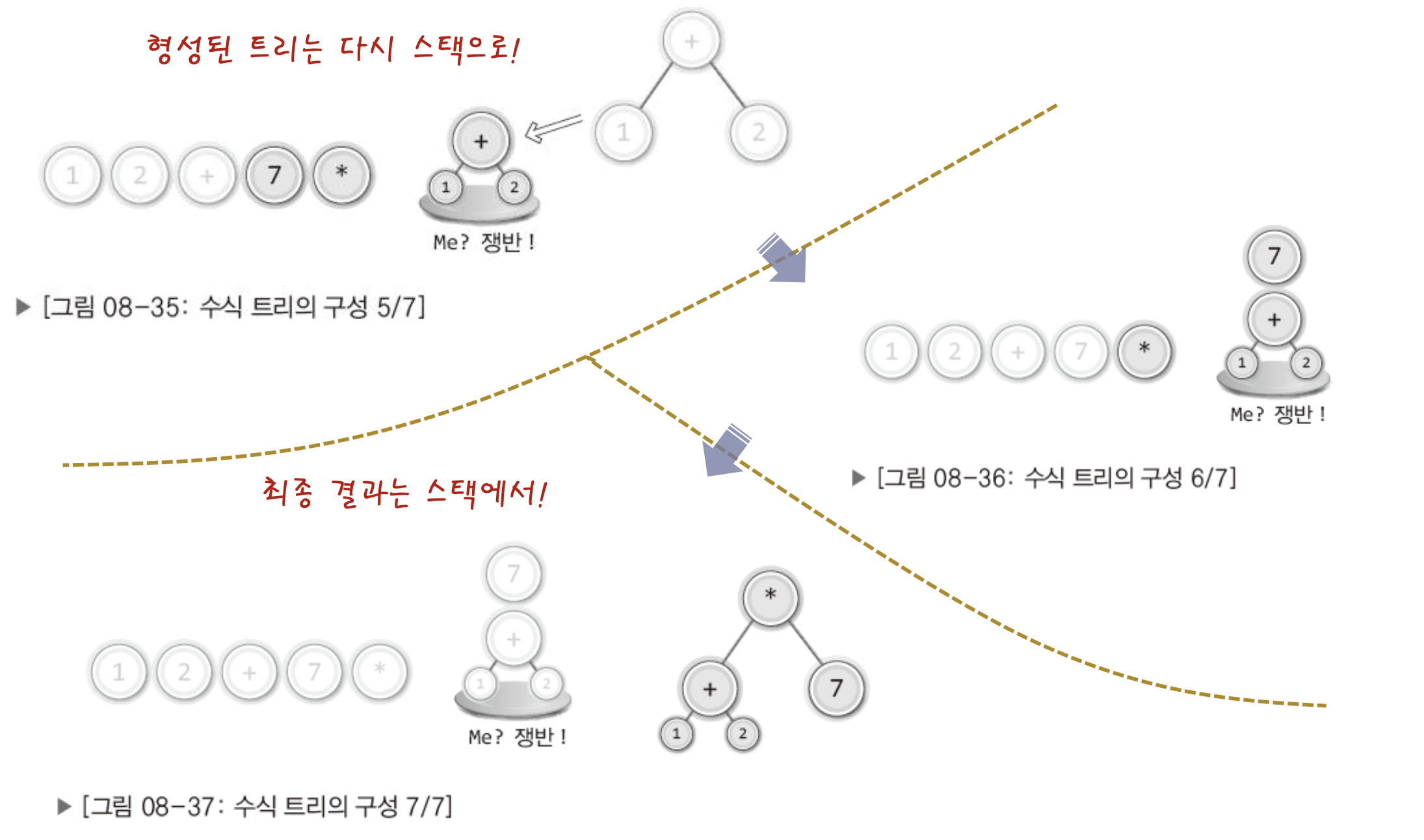
이 과정을 정리하자면
- 피연산자를 만나면 무조건 스택으로 옮긴다.
- 연산자를 만나면 스택에서 두 개의 피연산자를 꺼내어 자식 노드로 연결한다.
- 자식 노드로 연결해서 만들어진 트리는 다시 스택으로 옮긴다.
기본 원리는 이것이 전부이다.
다만....
위에서 말하는 스택에 저장되어 있는 두 개의 피연산자는 노드 또는 트리 라는 사실에만 주의하면 된다!
그럼...이제 코드를 짜보자

어떤가?
이전에 만들었던것들을 활용하니 이렇게 간단하게 만들 수 있다.
하지만 아직 확인할 방법이 없으므로 순회를 통해 출력하며 확인하자.
expressionTree.h
#ifndef __EXPRESSION_TREE_H__
#define __EXPRESSION_TREE_H__
#include "BinaryTree2.h"
BTreeNode * MakeExpTree(char exp[]);
int EvaluateExpTree(BTreeNode * bt);
void ShowPrefixTypeExp(BTreeNode * bt);
void ShowInfixTypeExp(BTreeNode * bt);
void ShowPostfixTypeExp(BTreeNode * bt);
#endifexpressionTree.c
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <ctype.h>
#include "ListBaseStack.h"
#include "BinaryTree2.h"
BTreeNode * MakeExpTree(char exp[])
{
Stack stack;
BTreeNode * pnode;
int expLen = strlen(exp);
int i;
StackInit(&stack);
for(i=0; i<expLen; i++)
{
pnode = MakeBTreeNode();
if(isdigit(exp[i])) // ««ø¨ªÍ¿⁄∂Û∏È...
{
SetData(pnode, exp[i]-'0');
}
else // ø¨ªÍ¿⁄∂Û∏È...
{
MakeRightSubTree(pnode, SPop(&stack));
MakeLeftSubTree(pnode, SPop(&stack));
SetData(pnode, exp[i]);
}
SPush(&stack, pnode);
}
return SPop(&stack);
}
int EvaluateExpTree(BTreeNode * bt)
{
int op1, op2;
if(GetLeftSubTree(bt)==NULL && GetRightSubTree(bt)==NULL)
return GetData(bt);
op1 = EvaluateExpTree(GetLeftSubTree(bt));
op2 = EvaluateExpTree(GetRightSubTree(bt));
switch(GetData(bt))
{
case '+':
return op1+op2;
case '-':
return op1-op2;
case '*':
return op1*op2;
case '/':
return op1/op2;
}
return 0;
}
void ShowNodeData(int data)
{
if(0<=data && data<=9)
printf("%d ", data);
else
printf("%c ", data);
}
void ShowPrefixTypeExp(BTreeNode * bt)
{
PreorderTraverse(bt, ShowNodeData);
}
void ShowInfixTypeExp(BTreeNode * bt)
{
InorderTraverse(bt, ShowNodeData);
}
void ShowPostfixTypeExp(BTreeNode * bt)
{
PostorderTraverse(bt, ShowNodeData);
}Main.c
//
// main.c
// ExpressionTree
//
// Created by 서희찬 on 2021/04/08.
//
#include <stdio.h>
#include "ExpressionTree.h"
int main(void)
{
char exp[] = "12+7*";
BTreeNode * eTree = MakeExpTree(exp);
printf("전위: ");
ShowPrefixTypeExp(eTree); printf("\n");
printf("중위: ");
ShowInfixTypeExp(eTree); printf("\n");
printf("후위: ");
ShowPostfixTypeExp(eTree); printf("\n");
printf("연산결과˙: %d \n", EvaluateExpTree(eTree));
return 0;
}
출력 결과 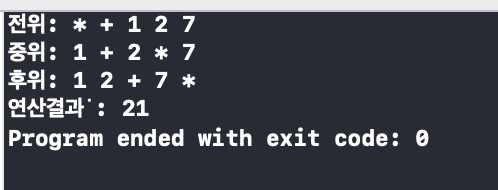
성..공..
이부분은 좀 어렵따...
강의 듣고와야겠따... 역시 트리를 쉽게 이겨내진 못했다..
--- 강의 ---
재귀적인 사고가 매우 중요하다.
그리고 재귀를 통해서 탈출조건을 만들어야한다는 사고도 재귀를 사용할때 붙어와야한다.
노드..서브트리...피연산자.. 으악!!!