이진 탐색 트리의 이해
이진 트리의 구조를 보면, 트리는 탐색에 효율적이라는 사실을 쉽게 알 수 있다.
저장된 데이터의 수가 10억 개 수준에 이른다 해도!!
트리의 높이는 30을 넘지 않기 때문이다!!
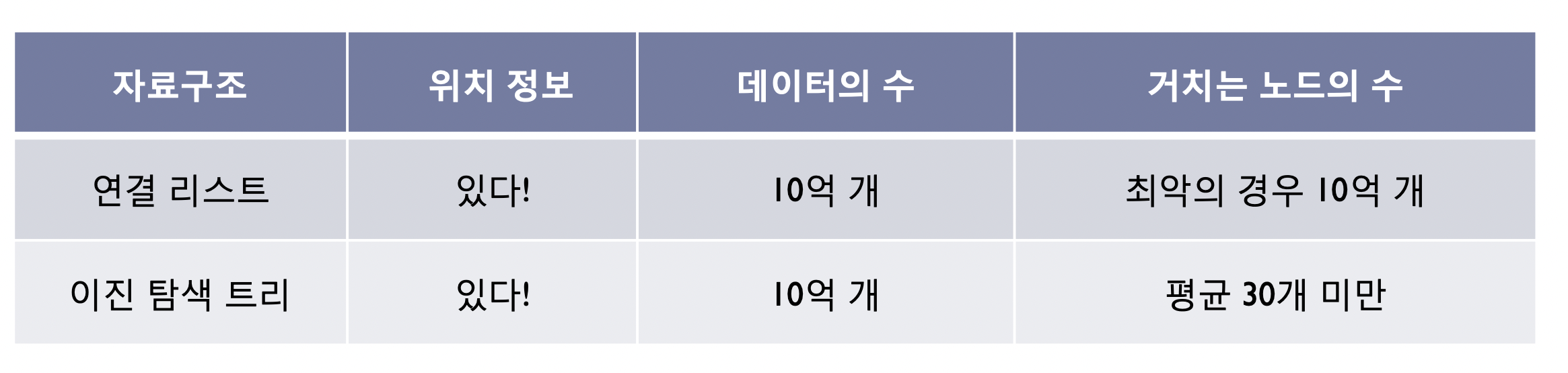
우리가 찾는 데이터가 리스트의 정중앙에 위치한다는 정보를 가지고 있음에도 10억개의 노드중 5억개를 지나야한다.
반면 이진트리는 30개의 노드만 지나면된다!
그러나..
"이진 트리는 단만 노드에 이르는 길의 갈래가 매우 많다. 따라서 찾는 데이터가 존재하는 제대로 된 길을 선택할 수 있어야 한다.
그러므로!
"이진 탐색 트리에는 데이터를 저장하는 규칙이 있다.
그리고 그 규칙은 특정 데이터의 위치를 찾는데 사용할 수 있다."
쉽게 말해서
이진 트리에 "데이터의 저장 규칙"을 더해놓은 것이 "이진 탐색 트리"이다!
탐색 트리가 되기 위한 조건
- 이진 탐색 트리의 노드에 저장된 키는 유일하다.
- 루트 노드의 키가 왼쪽 서브 트리를 구성하는 어떠한 노드의 키보다 크다.
- 루트 노드의 키가 오른쪽 서브 트리를 구성하는 어떠한 노드의 키보다 작다.
- 왼쪽과 오른쪽 서브 트리도 이진 탐색 트리이다.
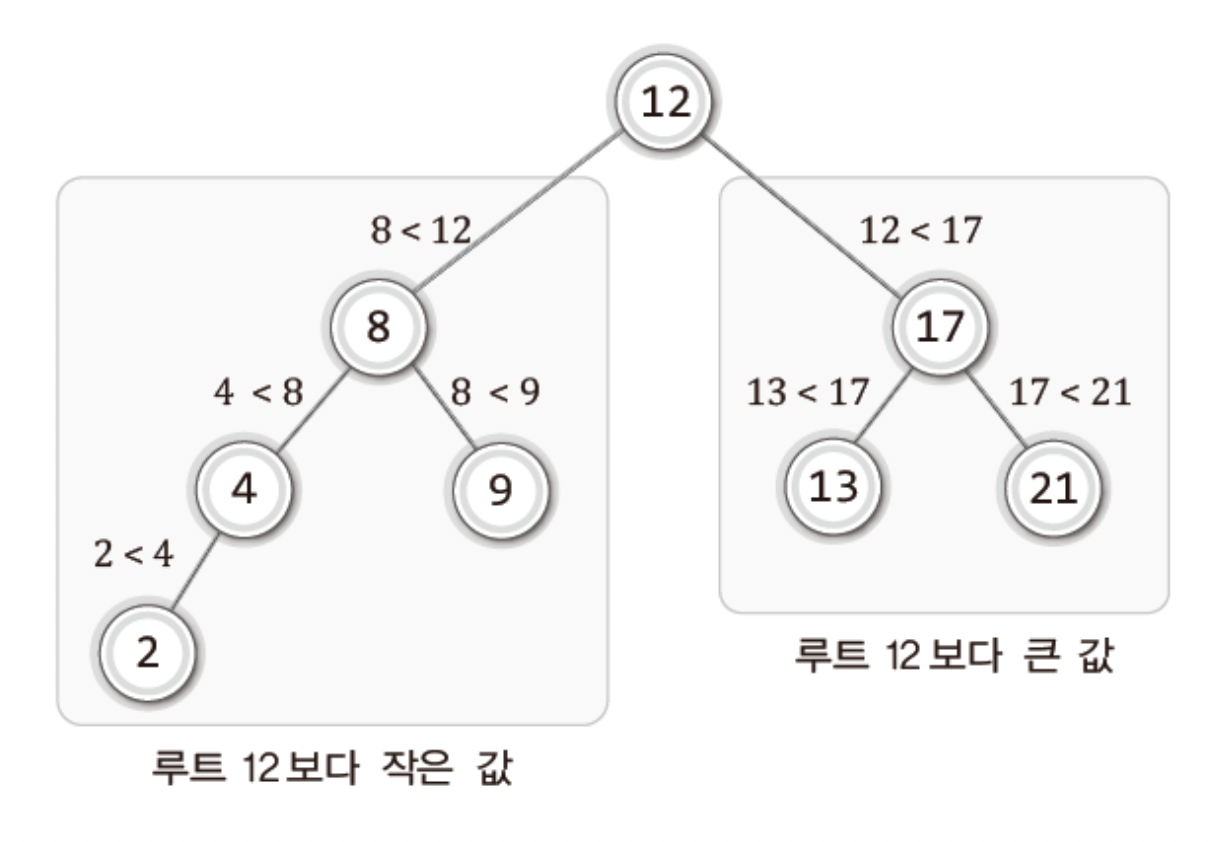
조건을 만족하는 그림이다 !
위의 그림을 통해 다음 수식이 언제~나 어디~서나 만족함을 볼 수 있다.
왼쪽 자식 노드의 키< 부모 노드의 키 < 오른쪽 자식 노드의 키
이 수식을 통해 위의 그림 이진 트리에 10을 저장한다고 생각해보자!
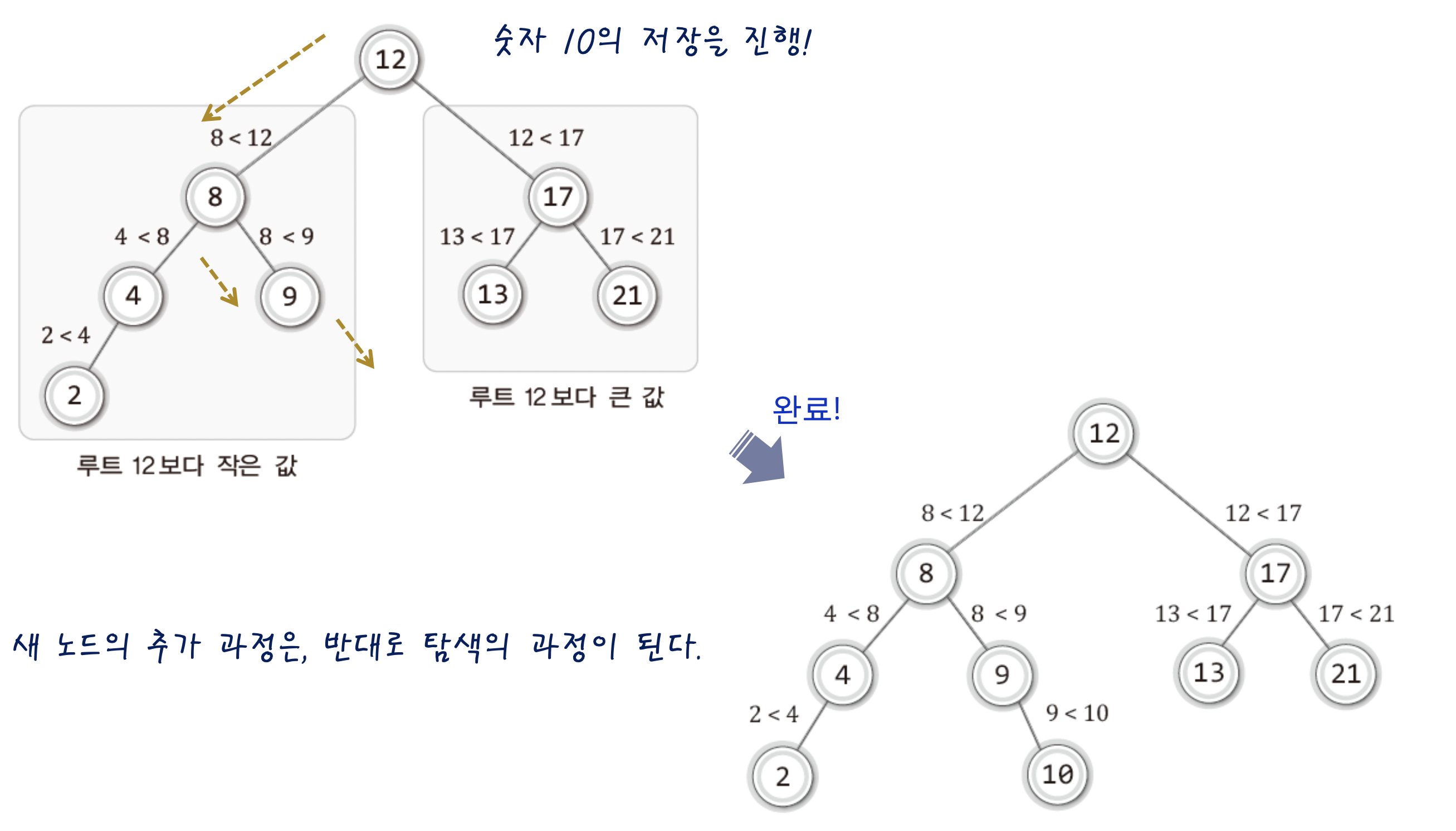
- 1단계 : 10<12 이므로 왼쪽 자식 노드로 이동
- 2단계 : 10>8이므로 오른쪽 자식 노드로 이동
- 3단계 : 10>9이므로 오른쪽 자식 노드로 이동
- 4단계 : 오른쪽에 아무것도 없으니 그 위치에 저장~
이렇듯 이진 탐색 트리는 "작으면 왼쪽! 크면 오른쪽!"라는 원칙을 기준으로 데이터를 삽입한다.
따라서 이진탐색 트리는 길을 잃을 일이없다!
그리고 금방 찾을 수 있다!!!
그러니 효율은 두말할 필요 없지 않겠는가!!!!
