탐색의 이해
탐색
다시말해서 "데이터를 찾는 방법"이다.
탐색은 트리의 뒷 이야기에 해당한다.
탐색은 알고리즘보다 자료구조에 더 가까운 주제이다!
이유는
"효율적인 탐색을 위해서는 "어떻게 찾을까"만을 고민해서는 안되고
"효율적인 탐색을 위한 저장방법이 무엇일까"를 우선적으로 고민해야한다.
효율적인 탐색이 가능한 대표적인 저장방식은 "트리"이다.
그러므로 대부분 트리의 연장선상이다!
탐색은! 컴싸에서 매우 중요한 위치를 차지하고있다.
보간 탐색(Interpolation Search)
우리는 앞서 다음 두 가지 탐색 알고리즘을 접했다
- 순차 탐색 : 정렬되지 않은 대상을 기반으로 하는 탐색
- 이진 탐색 : 정렬된 대상을 기반으로 하는 탐색
이 중 이진 탐색은 찾는 대상의 위치와 상관없이 일관 되게 반씩 줄여가면서 탐색을 진행하기에 대상의 위치에 따라 탐색의 효율에 차이가 발생한다.
그러나!
보간 탐색은 이러한 이진 탐색의 비효율성을 개선시킨 알고리즘이다.
이진 탐색처럼 그냥 중앙에서 탐색을 시작하지말고, 탐색대상이 앞쪽에 위치해 있으면 앞쪽에서 탐색을 시작하자 !
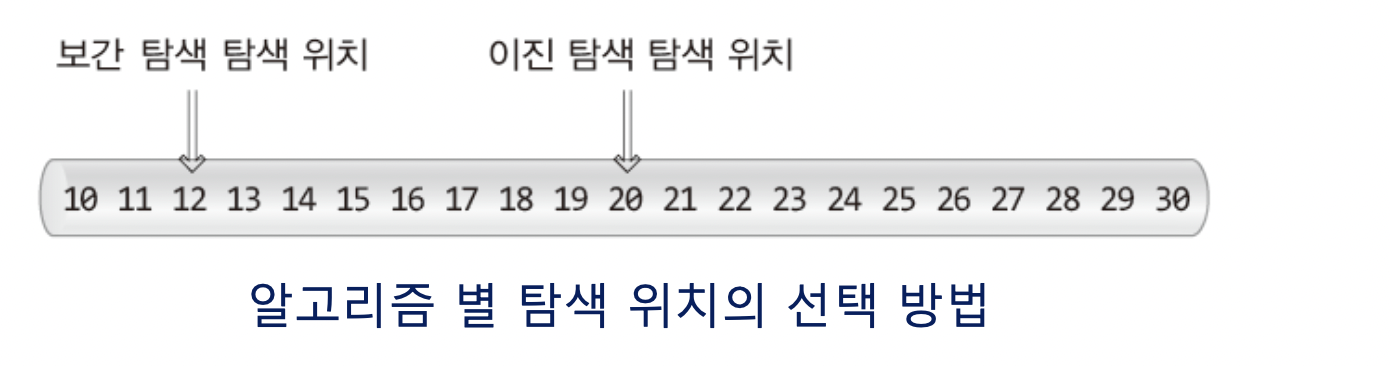
보간 탐색은 앞쪽에서 찾고
이진은 무조건 중간에서!
그러므로 당연빠따로 이진 탐색보다 속도가 뛰어나다.
이러한 특성때문에 보간 탐색은 전화번호부나 사전에 비유된다!
예를들어 "서희찬"라는 사람의 전화번호를 찾을 때 이진 탐색의 경우처럼 중심부를 펼쳐 찾는 사람은 없다!
"ㅅ" 에 해당하는 부분을 보고 찾을것이다!
이제 고민해야 할 것은 보간 탐색의 탐색위치를 결정하는 방법이다.

보간 탐색은
데이터 값과 그 데이터가 저장된 위치의 인덱스 값이 비례한다고 가정한다!
그렇기에 구한 값에 x에 찾는 값을 삽입하여 탐색 위치 s를 구하는 식이 완성되었다.
보간 탐색 구현에 앞서 하나를 배우고 가자!
탐색 키와 탐색 데이터
typedef int Key; // 탐색 키에 대한 타입뎁 선언
typedef double Data; // 탐색 데이터에 대한 타입뎁 선언
typedef struct item
{
Key searchKey; // 탐색 키
Data searchData; // 탐색 데이터
}Item;구조체 Item의 맴버는 탐색키와 탐색 데이터로 이뤄져 있다.
우리는 현재 자료구조를 공부하는 동안에는 다음 문장이 말하는 방식으로의 탐색이 진행된다고 생각하기 쉽다.
"다음 배열에서 숫자 3을 찾아야지!"
하지만! 이는 웃기지 않는가!?
이미 숫자 3을 가지고 있으면서 숫자3을 찾는다니!! ㅏㅎ하!
여기는 그저 배열안에 이 숫자의 유무확인밖에 없지 않는가!
따라서 의미 있는 방식으로의 탐색은 다음과 같다.
"사번이 7인 직원의 정보를 찾아야지"
여기서 사번은 "탐색 키" 이고 직원의 정보는 "탐색 데이터"이다!
하지만 우리는 소스코드와 설명의 편의상 정수로 진행한다!
그리고
"탐색 키는 그 값이 고유해야합니다."
그냥 정의 같은거니 토달지 말자!
보간 탐색의 구현
#include <stdio.h>
int ISearch(int ar[],int first,int last, int target)
{
int mid;
if(first > last)
return -1;
//이진 탐색과의 차이점을 반영한 문장
mid = ((double)(target-ar[first])/(ar[last]-ar[first])*(last-first))+first;
if(ar[mid]==target)
return mid;
else if(target<ar[mid])
return ISearch(ar, first, mid-1, target);
else
return ISearch(ar, mid+1, last, target);
}
int main(void)
{
int arr[]={1,3,5,7,9};
int idx;
idx = ISearch(arr, 0, sizeof(arr)/sizeof(int)-1, 7);
if(idx == -1)
printf("탐색 실패 \n");
else
printf("타겟 저장 인덱스 : %d \n",idx);
idx = ISearch(arr, 0, sizeof(arr)/sizeof(int)-1, 10);
if(idx==-1)
printf("탐색 실패 \n");
else
printf("타겟 저장 인덱스 : %d \n",idx);
return 0;
}
3은 찾고 10은 못찾는것을 볼수있다.
이진 탐색과 탐색의 대상을 선정하는 방법만의 차이점이므로 이진 탐색의 소스에 mid부분만 위에서 구한 공식으로 바꿔주기만 하면된다!
하지만.. 이 코드에 문제점이 있다.
idx = ISearch(arr, 0, sizeof(arr)/sizeof(int)-1, 2);
로 실행해보면 
탈출하지 못하는것을 알수있는데
이는 ISarch 함수의 다음 탈출 조건을 만족하지 못해서이다.
if(first>last)
return -1;그래서 우리는 이와같이 변경해줘야한다.
if(ar[first]>target || ar[last]<target)
return -1;탐색 대상이 존재하지 않는 경우, ISearch 함수가 재귀적으로 호출됨에 따라 target에 저장된 값은 first와 last가 가리키는 값의 범위를 넘어서게 된다.
정렬된 탐색대상의 범위를 좁혀가면서 정렬을 진행하기 때문이다!
first last가 target을 향해서 점점 좁혀가지 않는가!!
그래서 이렇다 !
탈출조건을 만족하지 않는 이유
int arr[]={1,3,5,7,9};
..
Isearch(arr,1,4,2); // 배열 arr의 인덱스 1-4범위 내에서 숫자 2탐색가 호출되었다고 생각해보자
first = 1
last = 4
target = 2 이다.
이 값을 mid에 계산해보면 당연빠따로 mid에 0이 저장된다.
인덱스 1~4범위 내에서 최댓값과 최솟값은 각각 3과 9이기때문이다!
그런데.. 타겟은 2이다.
즉, 그 값이 탐색범위 내에 위치하지 못할 만큼 작다!!!!
그러니 가장 왼쪽 값이랑 비교해봐라고 0을 mid에 주는것은 타당하다 !
하지만..
이 결과가
else
return ISearch(ar, mid+1, last, target);이 문장과 만나고 나면
Isearch(arr,1,4,2); 가 다시 실행되어 탈출하지 못한다!
그래서
"탐색대상이 존재하지 않을 경우, 탐색대상의 값은 탐색범위의 값을 넘어선다."는 사실에 근거하여
if(ar[first]>target || ar[last]<target) return -1;로 수정해야한다 !!
무엇보다 target에 저장된 값이 first,last가 가리키는 값의 범위를 넘어선다는 사실이 매우중요하다 !
