이진 탐색 트리의 삭제 구현: 삭제에 대한 이론적 설명과 구현 일부
이제 대망의 삭제에 대해 배워보자 !
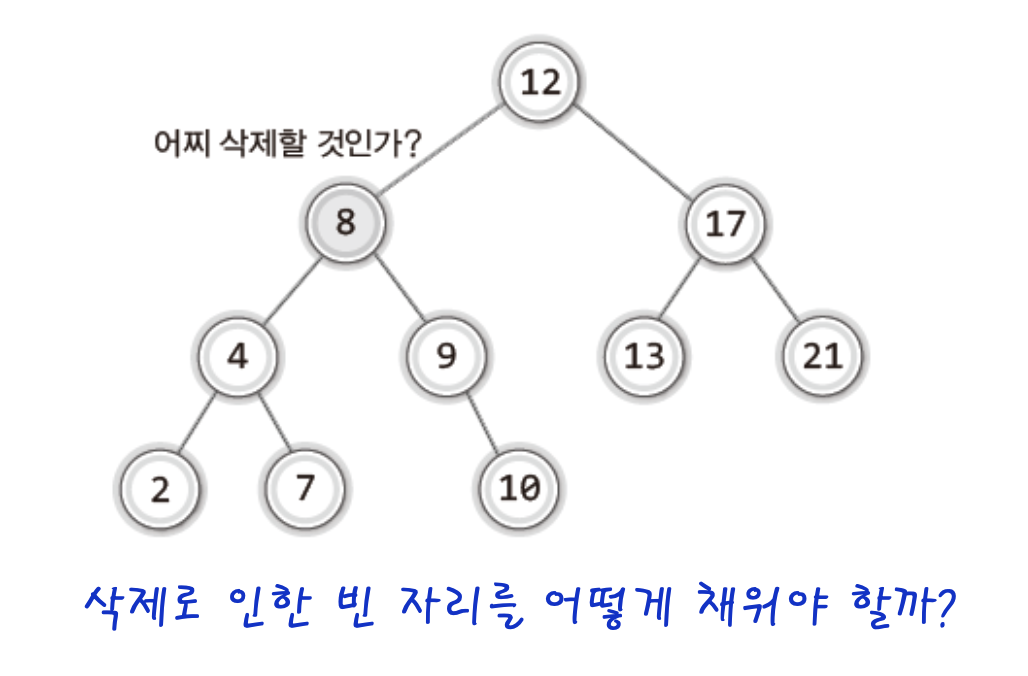
위 그림에서 8을 삭제한다고 하면 삭제 한 후 이 자리를 누군가 대신 채워여만 이진 탐색 트리가 유지되므로 어떻게 이 빈자리를 채워야 할지가 이진 탐색트리의 삭제가 어랴운 이유중 하나이다.
단말노드라면 그저 삭제하면 되지만 아니라면 고민이 필요하다
이에 따라 경우의 수들을 생각해보자
- 경우 1 : 삭제할 노드가 단말 노드일 경우 // 제일 단순 !
- 경우 2 : 삭제할 노드가 하나의 자식 노드를(서브트리) 갖는 경우
- 경우 3 : 삭제할 노드가 두개의 자식 노드(서브트리)를 갖는 경우
총 3가지이지만 루트 노드인 경우와 그렇지 않은 경우도 나눠야 하기 때문에 최대 6가지로 구분할 수도 있다.
그럼 상황별 삭제에 대해 알아보자 !
- 상황 1
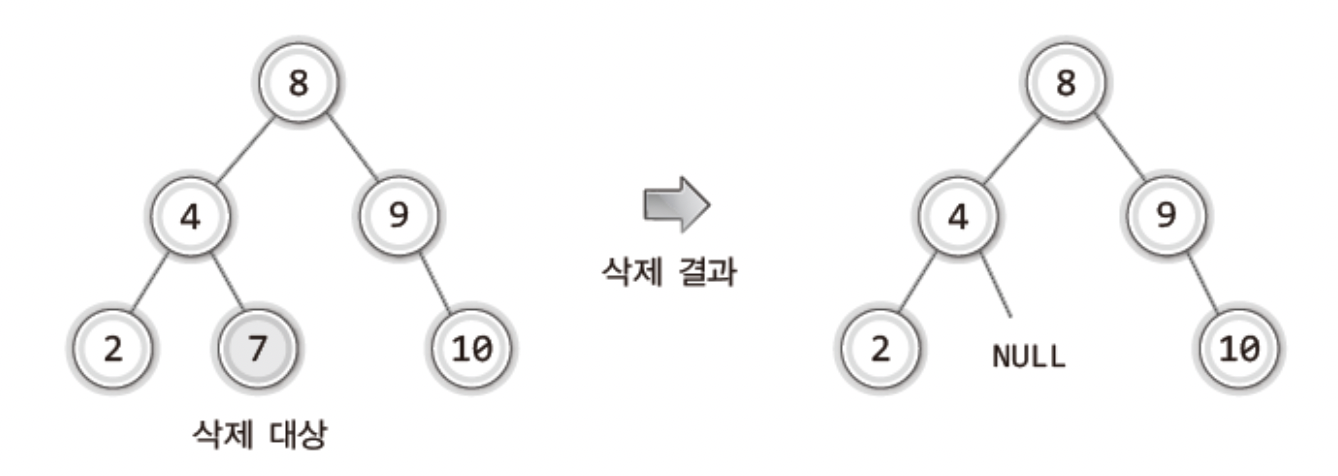
보이다 싶이 제일 간단해보이지 않는가!
그냥 단말 노드를 삭제하는것으로 삭제의 과정이 완료된다.
이에 대한 코드는 다음과 같이 구성하면 된다.
보이다 싶이 그저 삭제할 노드가 단말노드이면 그 부모노드의 left/right중 삭제할 노드인 것을 삭제해주면 된다.
RemoverRight/leftSubTree()함수는 아직 정의 한 봐 없는 함수들이기에 이에 관해 간단히 정리만 해주겠다.
- RemoverRightSubTree(pNode) : pNode가 가리키는 노드의 왼쪽 자식 노드 트리에서 제거
- RemoverleftSubTree(pNode) : pNode 가 가리키는 노드의 오른쪽 자식 노드 트리에서 제거
이제 상황2를 보여주겠다.
- 상황 2
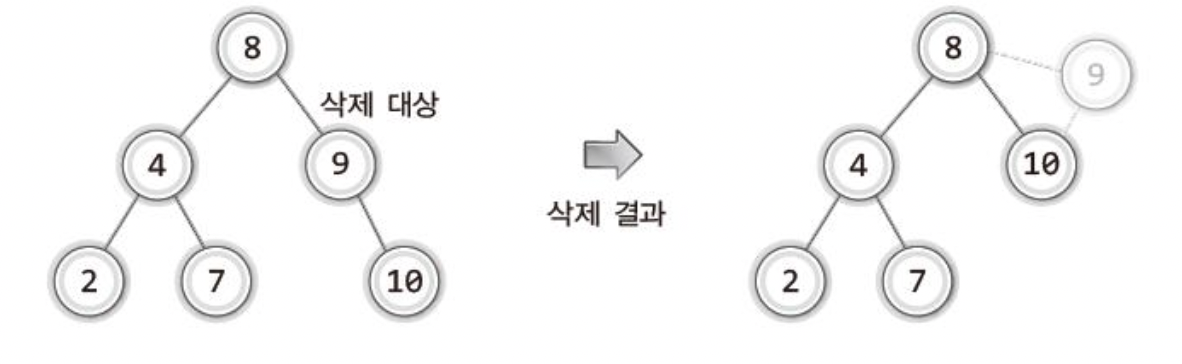
보이듯이 상황2 에서는 부모 노드와 자식 노드를 연결하는 것이 관건이다 !
하지만 여기에 무엇보다 주의해야할 한가지 사항이 있다.
"위 그림의 10은 무조건! 상관없이 ! 8이 저장된 노드의 오른쪽 자식 노드가 되어야한다"
이는 10을 저장하는 노드가 9를 저장하는 노드를 대신하기 때문이다!
즉 그냥 9가 저장한 노드를 10이 대신한다고 생각하자 !
이를 통해 코드르 짜보자 !
삭제할 부모 노드가 가리키는 자식 노드를 dcNdoe에 저장하고 이를 부모노드와 교체하는 코드이다.
- changeLeft/RightSubTree : MakeLeft/RightSubTree와 유사하다.
이 또한 나중에 정의하고 설명하겠다.
간단히 설명하자면 Make 와 다른점은 메모리 소멸 과정을 동반하냐 안하냐 이다.
이제 마지막 상황3에 대해 알아보자 !
상황 3
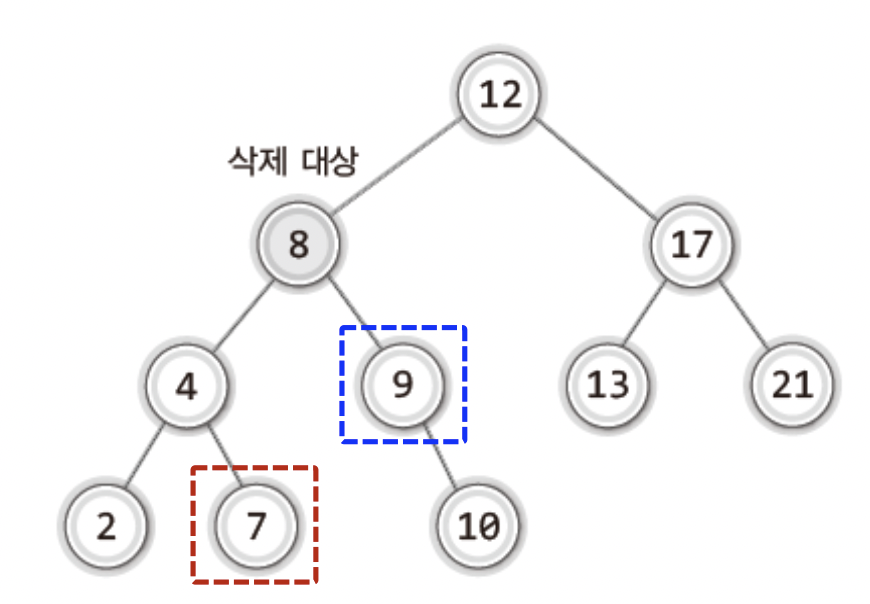8을 삭제하면 이 위치를 무엇으로 채울지 생각해보자
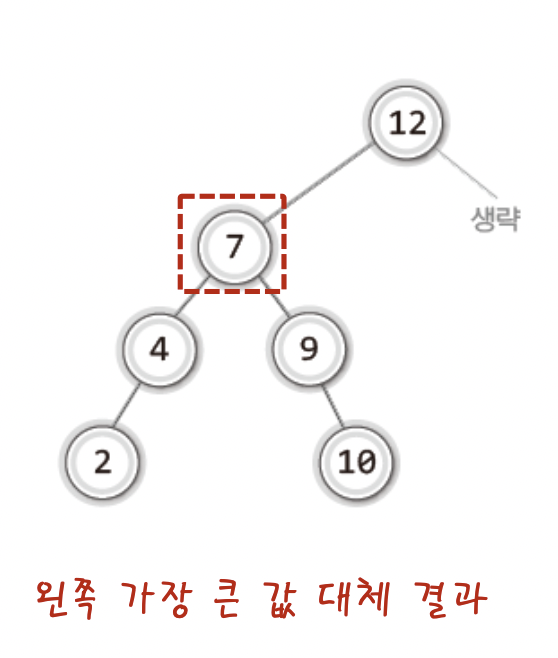
- 8이 저장된 노드의 왼쪽 서브트리에서 가장 큰 값인 7
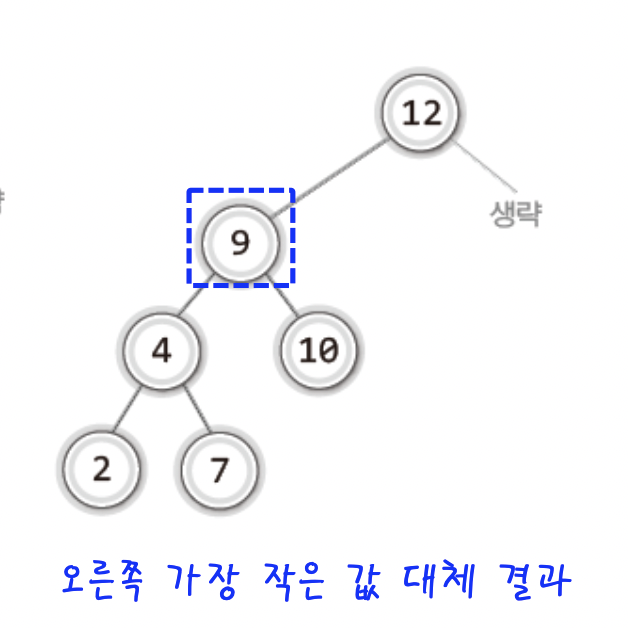
- 8이 저장된 노드의 오른쪽 서브트리에서 가장 큰 값인 9
이처럼 왼쪽이나 오른쪽에서 가장 큰 값으로 대체 하면된다!
서브 트리에서 가장 큰 값이나 작은 값을 저장한 노드를 찾는 법을 보여주게따
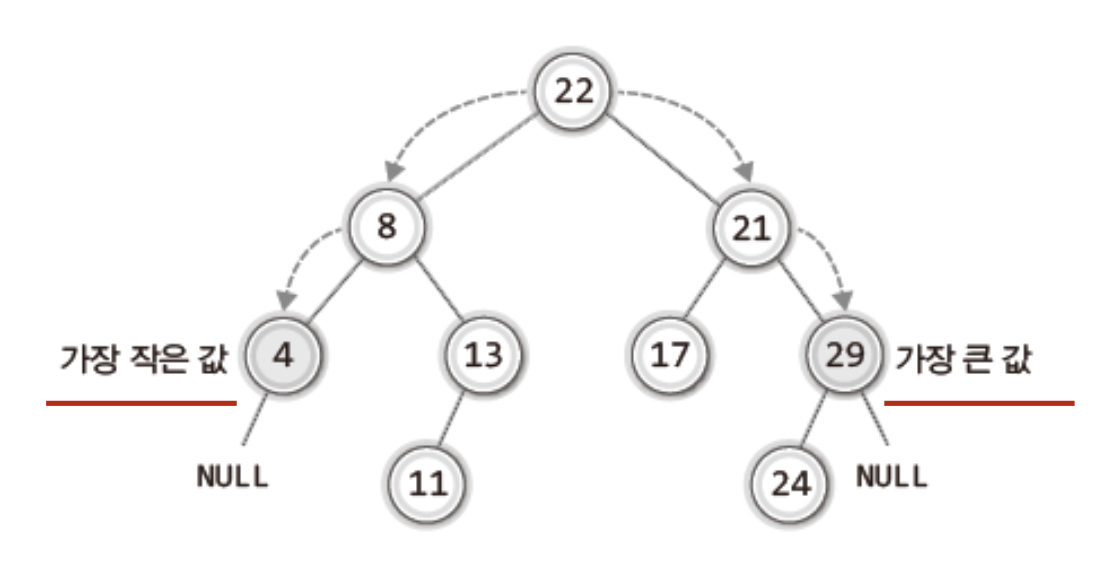
그냥 젤 왼쪽으로 NULL을 만날때까지 계쏙 가면 작은 값
반대로는 큰 값을 찾을 수 있다.
이것을 설명한 이유는
상황3에서 삭제할 노드의 "왼쪽 서브 트리에서 가장 큰 값을 저장한 노드" 나 "오른쪽 서브 트리에서 가장 작은 값을 저장한 노드"로 대체하면 된다.
어느것으로 하든! 이진 탐색 트리의 유지에는 지장이 없다.
그러므로 우리는 다음과 같은 방법을 선택하자.
"삭제할 노드의 오른쪽 서브 트리에서 가장 작은 값을 지니는 노드를 찾아서 이것으로 삭제할 노드를 대체한다"
이 내용을 기준으로 그림을 보자 .
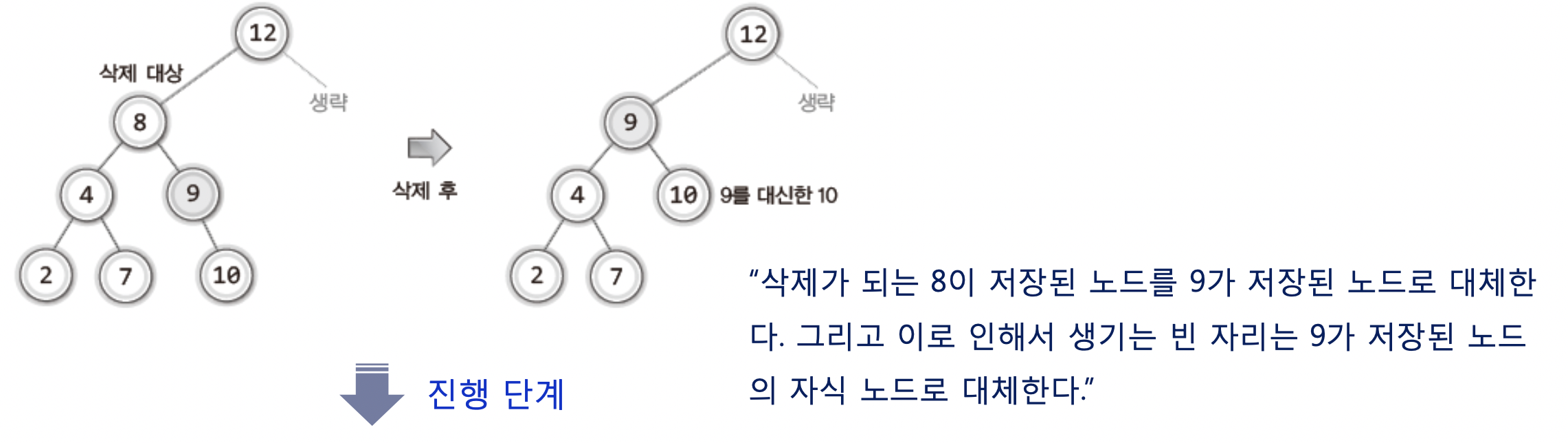
"삭제가 되는 8이 저장된 노드를 9가 대체하고 이로 인해 생기는 빈자리도 9가 저장된 노드의 자식노드로 대체한다"
가 위의 삭제과정에서 할일이다.
이를 위해 이 방법을 적용하자.
위 과정은 9를 8이 저장된 노드에 가져다 놓지 않고
그저 "값의 대입"을 통해 노드의 교체를 대신하고 있다.
이를 통해서 삭제 대상인 8이 저장된 노드의 부모 노드와 자식 노드의 연결을 유지하기 위해서 별도의 코드를 삽입할 필요가 없다.
그럼 이런 생각이 들것이다.
"10이 저장된 노드는 위와 달리 9가 저장된 노드에 대입해버리면 간단한거 아닌가요? 새로운 연결을 구성할 필요가 없나요?"
멋진 생각이긴 하지만 이렇게 하면 문제가 발생한다.
"10을 저장하고 있는 자식 노드가 단말 노드가 아닌 경우를 생각해야한다!
단말 노드가 아니라면 단순 대입으로 노드의 대체를 대신 할 수 없다! "
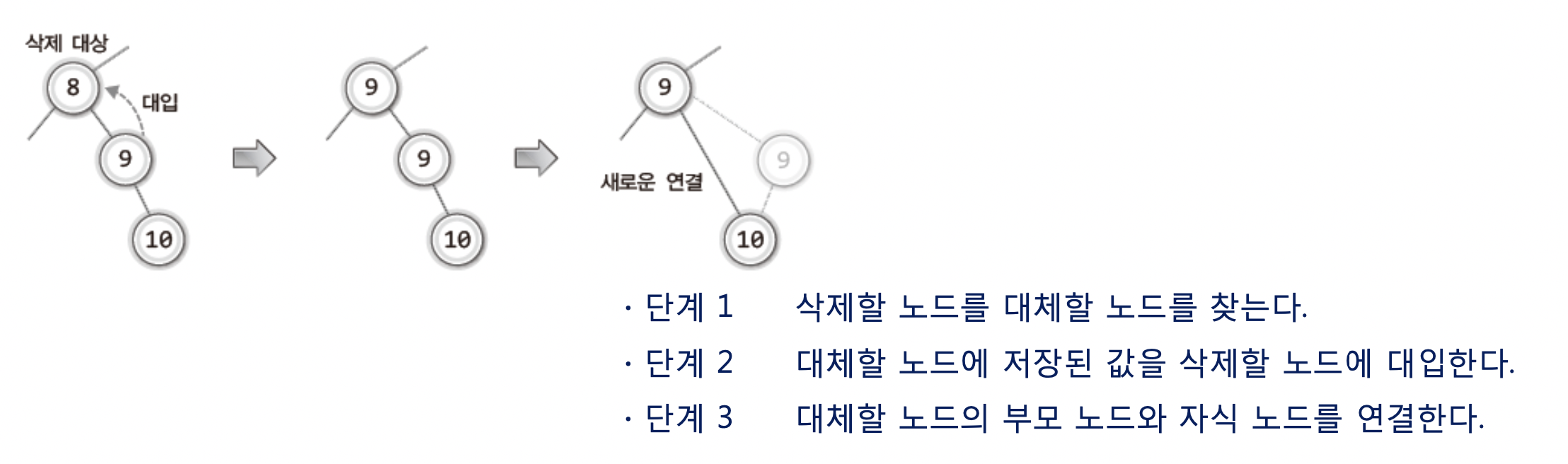
이를 바탕으로 정리한 단계가 위 그림에 나온
- 단계 1 : 삭제할 노드를 대체할 노드를 찾는다.
- 단계 2 : 대체할 노드에 저장된 값을 삭제할 노드에 대입한다.
- 단계 3 : 대체할 노드의 부모노드와 자식 노드를 연결한다.
이제 이를 코드로 옮겨보자.
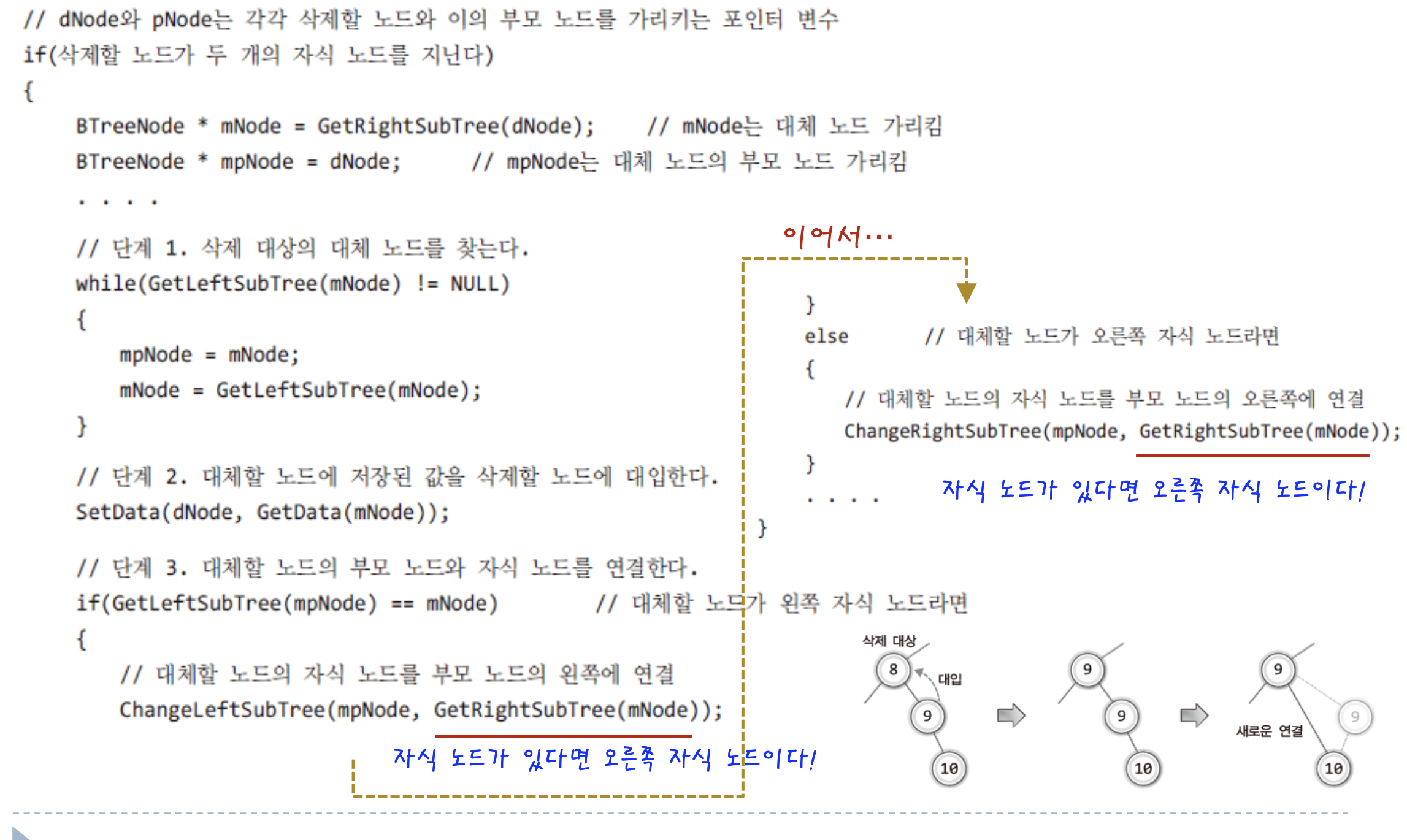
음.. 좀 길다 .. !
그치만 위의 설명들을 그대로 코드에 옮긴것에 불과하다.
그런데
GetRightSubTree(mNode)가 두번 호출되서
잘못된것이라고 생각들수도 있는데 이는 맞는거다.
그 이유는
"삭제할 노드의 오른쪽 서브트리에서 가장 작은 값을 지니는 노드를 찾아서 이것으로 삭제할 노들르 대체한다."
가장 작은 ㄱ밧을 지니는 노드를 찾으려면 NULL을 만날때까지 왼쪽 자식 노드로 계속해서 이동해야한다!
그러니 자식 노드가 있다면 오른쪽 자식노드가 아니겠는가!!!
이제 다음 포스트에서
삭제의 구현을 위해 이진 트리를 확장하고 구현해보자.
