[자료구조]탐색 2 (12-2-4) AVL트리의 구현

서희찬·2021년 4월 21일

윤성우의 열혈 자료구조

목록 보기

45/57

리밸런싱의 도구 AVLRebalance.h,c

이제 만든 도구들을 모아둔 헤더/소스 파일을 보이겠다 !
AVLRebalance.h

//
//  AVLRebalance.h
//  AVLTree
//
//  Created by 서희찬 on 2021/04/21.
//

#ifndef AVLRebalance_h
#define AVLRebalance_h

#include "BinaryTree3.h"

// 트리의 균형을 잡는다.
BTreeNode * Rebalance(BTreeNode ** pRoot);

#endif /* AVLRebalance_h */

AVLRebalance.c

//
//  AVLRebalance.c
//  AVLTree
//
//  Created by 서희찬 on 2021/04/21.
//
#include <stdio.h>
#include "BinaryTree3.h"

BTreeNode * RotateLL(BTreeNode *bst)
{
    BTreeNode * pNode; // parent node
    BTreeNode * cNode; // child Node
    
    // pNode, cNode 가리키기
    pNode = bst;
    cNode = GetLeftSubTree(pNode);
    
    // real LL rotate
    ChangeLeftSubTree(pNode, GetRightSubTree(cNode));
    ChangeRightSubTree(cNode, pNode);
    
    //LL회전으로 cNode가 루트 노드가 됨! 그러므로 변경된 루트노드 주소값 반환
    return cNode;
}

BTreeNode * RotateRR(BTreeNode *bst)
{
    BTreeNode * pNode; // parent node
    BTreeNode * cNode; // child Node
    
    // pNode, cNode 가리키기
    pNode = bst;
    cNode = GetRightSubTree(pNode);
    
    // real RR rotate
    ChangeRightSubTree(pNode, GetLeftSubTree(cNode));
    ChangeLeftSubTree(cNode, pNode);
    
    //RR회전으로 cNode가 루트 노드가 됨! 그러므로 변경된 루트노드 주소값 반환
    return cNode;
}

BTreeNode * RotateLR(BTreeNode*bst) // LR회전을 담당하는 함수
{
    BTreeNode * pNode; // parent Node
    BTreeNode * cNode; // child Node
    
    //pNode, cNode 가 LR회전을 위해 적절한 위치를 가리키게한다.
    pNode = bst;
    cNode = GetLeftSubTree(pNode);
    
    //실제 LR회전을 담당하는 두 개의 문장
    ChangeLeftSubTree(pNode, RotateRR(cNode)); // 부분적 RR회전
    return RotateLL(pNode); // LL회전
}

BTreeNode * RotateRL(BTreeNode*bst) // LR회전을 담당하는 함수
{
    BTreeNode * pNode; // parent Node
    BTreeNode * cNode; // child Node
    
    //pNode, cNode 가 RL회전을 위해 적절한 위치를 가리키게한다.
    pNode = bst;
    cNode = GetRightSubTree(pNode);
    
    //실제 RL회전을 담당하는 두 개의 문장
    ChangeRightSubTree(pNode, RotateLL(cNode)); // 부분적 LL회전
    return RotateRR(pNode); // LL회전
}

int GetHeight(BTreeNode * bst)
{
    int leftH; // left Height
    int rightH; // right Height
    
    if(bst == NULL)
        return 0;
    
    leftH = GetHeight(GetLeftSubTree(bst)); // 왼쪽 서브 트리 높이 계산
    rightH = GetHeight(GetRightSubTree(bst)); // 오른쪽 서브 트리 높이 계산
    
    // 큰 값의 높이를 반환한다.
    if(leftH > rightH)
        return leftH + 1;
    else
        return rightH + 1;
}

//두 서브 트리의 '높이의 차'를 반환
int GetHeightDiff(BTreeNode * bst)
{
    int lsh; // left sub tree Height
    int rsh; // right sub tree height
    
    if(bst == NULL)
        return 0;
    lsh = GetHeight(GetLeftSubTree(bst));
    rsh = GetHeight(GetRightSubTree(bst));
    return lsh - rsh;
}

BTreeNode * Rebalance(BTreeNode **pRoot)
{
    int hDiff = GetHeightDiff(*pRoot); // 균형 인수 계산
    
    //균형 인수가 +2 이상이면 LL/LR 상태이다.
    if(hDiff>1) // +2이상이면(왼쪽 서브 트리 방향으로 높이가 2 이상 크다면)
    {
        if(GetHeightDiff(GetLeftSubTree(*pRoot))>0)
            *pRoot = RotateLL(*pRoot);
        else
            *pRoot = RotateLR(*pRoot);
    }
    //균형 인수가 -2 이하이면 RR/RL 상태이다.
    if(hDiff<-1) // 오른쪽 서브 트리 방향으로 2 이상 크다면,
    {
        if(GetHeightDiff(GetRightSubTree(*pRoot))<0)
            *pRoot = RotateRR(*pRoot);
        else
            *pRoot = RotateRL(*pRoot);
    }
    
    return *pRoot;
}

이렇듯 헤더파일에는 필요한 선언만 하는것이 코드를 깔끔하게 쓸 수 있는 팁? 이다!

AVL 트리를 담고 있는 BinarySearchTree3.h,c

기존에 Insert/Remove 함수에
노드 추가 후 리밸런싱으로 그저 끝을 냈는데..

우리는 리밸런싱 함수가 반환하는 값이 무엇인지 알았으니 이를 *pRoot에 저장해줘야한다.

이런식으로 말이다.
하지만!
이는 오류가 있다.
바로 1,2,3,4,5... 저장될때

이런식으로 트리가 형성된다는 점이다.
어떤것이 문제인지 보이는가!?
바로

오직 "루트노드"기준 균형 인수가 안정적이고 나머지 노드들의 균형 인수는 신경쓰지 않았다.
그래서 4가 저장된 노드를 보면 균형인수가 -2이하 임에도 불구하고 리밸런싱이 일어나지 않는 것을 볼 수 있다.

그렇다면 이 오류를 어떻게 수정할것인가!?

이런 방식으로 새로 저장된 노드의 부모 노드들을 모두 살펴 저장된 노드를 기준으로 불균형 여부를 검사해야한다.
(위 그림에서는 3,4,5 물론 ! 3은 안해도 되지만 검사한다고 해서 문제가 되진 않는다.)

그렇다면 이를 어떻게 코드로 구현할까.. 생각해보면 이 역시 반복적으로 노드를 확인해야하므로..
재귀를 떠올릴 수 있다.

BTreeNode* BSTInsert(BTreeNode ** pRoot, BSTData data)
{
    if(*pRoot == NULL)
    {
        *pRoot = MakeBTreeNode();
        SetData(*pRoot, data);
    }
    else if(data < GetData(*pRoot))
    {
        BSTInsert(&((*pRoot)->left), data);
        *pRoot = Rebalance(pRoot);
    }
    else if(data > GetData(*pRoot))
    {
        BSTInsert(&((*pRoot)->right), data);
        *pRoot = Rebalance(pRoot);
    }
    else
    {
        return NULL; // 키의 중복은 허락하지 않는다( data == GetData(*pRoot)
    }
    return *pRoot;
}

어떤가!!
재귀의 위대함을 또 다시 느끼게되는 기회가 아닌가!
구현의 논리는 이렇다

루트 노드를 대상으로 하여 데이터의 저장을 시도한다(함수 호출!)
1-1. 루트 노드에 저장된 데이터와 새 데이터를 비교한다.
1-2. 비교 후 새 데이터의 값이 작으면 왼쪽 자식 노드를 루트 노드로 하여 데이터의 저장을 시도한다.
1-3. 새 데이터의 값이 크면 오른쪽에 !
1-4. 저장이 완료되면 해당 루트 노드를 기준으로 리밸런싱을 진행한다.

기본적으로 저장 후 리밸런싱의 단순 흐름을 재귀적으로 구성한 꼴이 되어서 새 노드가 추가된 경우 그 노드의 부모 노드들을 대상으로 불균형 여부를 확인한다!!!
이 것도 노드가 추가된 후에 진행한다 !

이 삽입함수만 수정해주면 예쁘게 트리가 짜여진다!

자 이제 Main 을 보고
모든 파일들을 보여주겠다.

AVL 트리가 리밸런싱을 제대로 하고 있는가?

main 을 보여주겠다.
AVLTreeMain.c

#include <stdio.h>
#include "BinaryTree3.h" // 트리구조 확인을 위해
#include "BinarySearchTree3.h"

int main(void)
{
    BTreeNode * avlRoot;
    BTreeNode * clNode; // current left Node
    BTreeNode * crNode; // current right Node
    
    BTreeNode * clNode2;
    BTreeNode * crNode2;

    BTreeNode * clNode3;
    BTreeNode * crNode3;
    
    BSTMakeAndInit(&avlRoot);
    
    BSTInsert(&avlRoot, 1);
    BSTInsert(&avlRoot, 2);
    BSTInsert(&avlRoot, 3);
    BSTInsert(&avlRoot, 4);
    BSTInsert(&avlRoot, 5);
    BSTInsert(&avlRoot, 6);
    BSTInsert(&avlRoot, 7);
    BSTInsert(&avlRoot, 8);
    BSTInsert(&avlRoot, 9);
    
    printf("루트 노드 : %d \n",GetData(avlRoot)); //4
    
    clNode = GetLeftSubTree(avlRoot); // 2
    crNode = GetRightSubTree(avlRoot); // 6
    printf("왼쪽 1 : %d, 오른쪽 1 : %d \n",GetData(clNode),GetData(crNode));
    
    clNode2 = GetLeftSubTree(clNode); // 1, 2의 왼쪽 노드
    crNode2 = GetRightSubTree(clNode);// 3, 2의 오른쪽 노드
    printf("왼쪽 2 : %d, 오른쪽 2 : %d \n",GetData(clNode2),GetData(crNode2));
    
    clNode2 = GetLeftSubTree(crNode); // 5, 6의 왼쪽 노드
    crNode2 = GetRightSubTree(crNode); // 8, 6의 오른쪽 노드
    printf("왼쪽 3 : %d, 오른쪽 3 : %d \n",GetData(clNode2),GetData(crNode2));
    
    clNode3 = GetLeftSubTree(crNode2); //7, 8의 왼쪽 노드
    crNode3 = GetRightSubTree(crNode2); // 9, 8의 오른쪽 노드
    printf("왼쪽 4 : %d, 오른쪽 4 : %d \n",GetData(clNode3),GetData(crNode3));
    
    return 0;
}

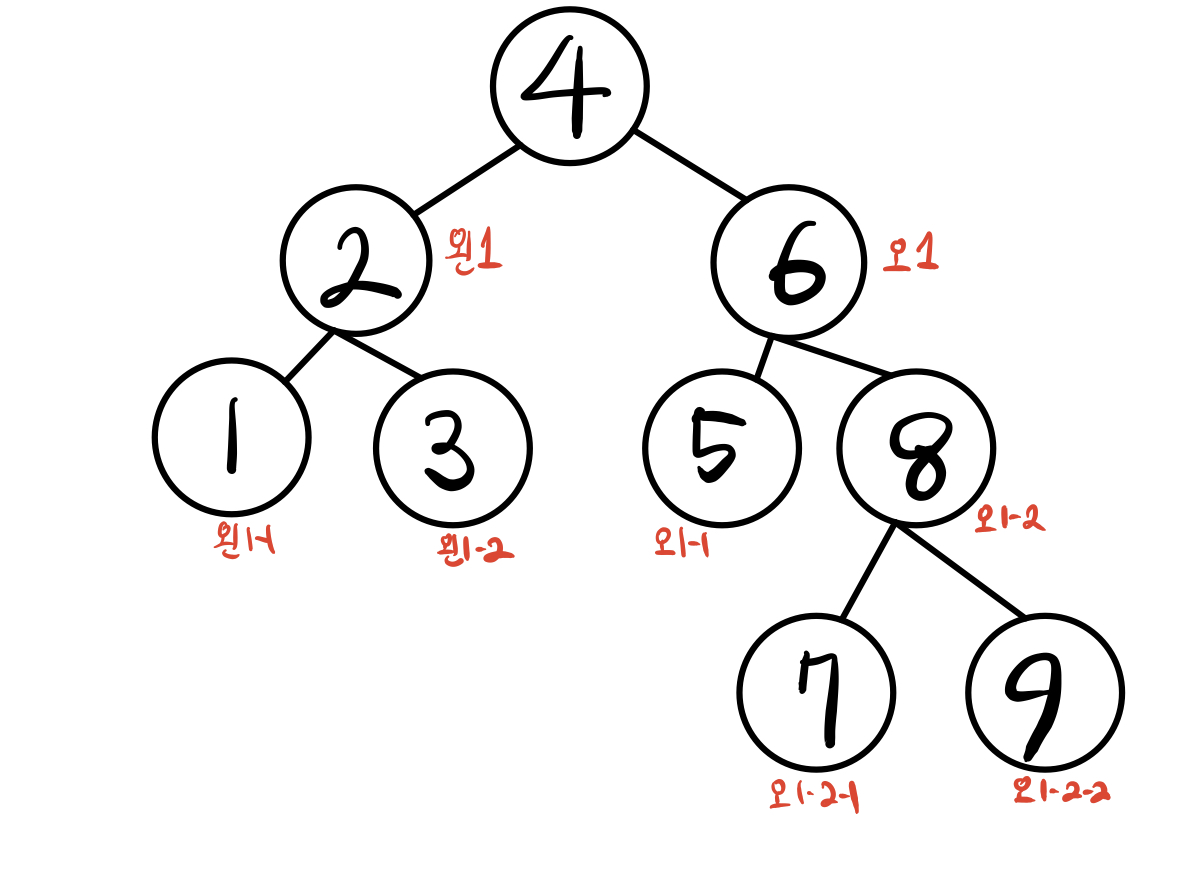
실행결과를 통해
이와 같아짐을 확인할 수 있다!

트리로 한번 확인해보자.

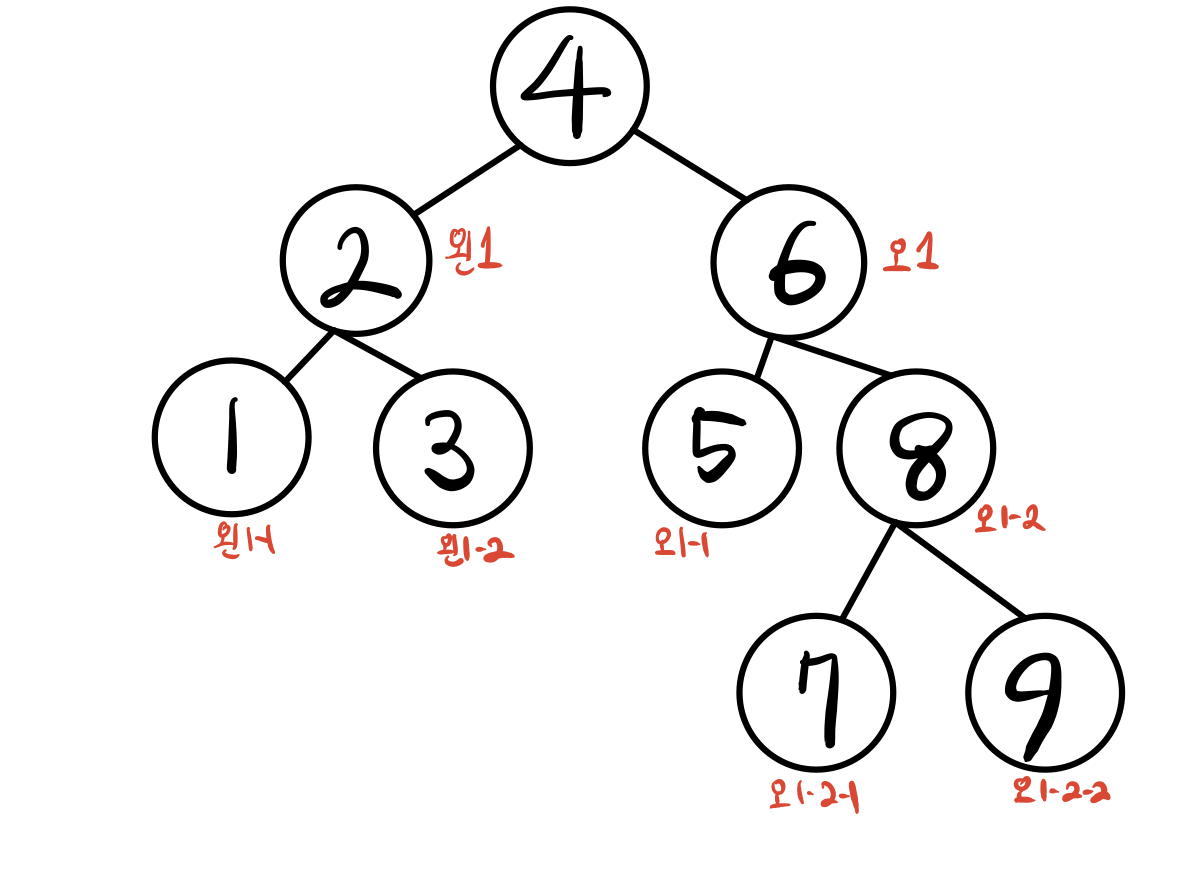
어떤가 균형 인수는 ... 적는걸깜박했지만!
전부 -1~+1 임을 알수있다.
이로써 !

트리와 관련 있는 이야기가 어느정도 마무리 되었고 탐색또한 마무리 되었다!!

수고했따!!!

BinarTree3.h,c BinarySearchTree3.h,c AVLRebalance.c,h , AVLTreeMain.c

총 7개의 파일이 필요하다.
이번포스트에서 보여주지않은
Binary3.h,c BinarySearchTree3.h,c 소스코드를 보여주고 마무리 짓겠다.

Binary3.h

#ifndef __BINARY_TREE3_H__
#define __BINARY_TREE3_H__

typedef int BTData;

typedef struct _bTreeNode
{
	BTData data;
	struct _bTreeNode * left;
	struct _bTreeNode * right;
} BTreeNode;

BTreeNode * MakeBTreeNode(void);
BTData GetData(BTreeNode * bt);
void SetData(BTreeNode * bt, BTData data);

BTreeNode * GetLeftSubTree(BTreeNode * bt);
BTreeNode * GetRightSubTree(BTreeNode * bt);

void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub);
void MakeRightSubTree(BTreeNode * main, BTreeNode * sub);

typedef void VisitFuncPtr(BTData data);

void PreorderTraverse(BTreeNode * bt, VisitFuncPtr action);
void InorderTraverse(BTreeNode * bt, VisitFuncPtr action);
void PostorderTraverse(BTreeNode * bt, VisitFuncPtr action);

BTreeNode * RemoveLeftSubTree(BTreeNode * bt);

BTreeNode * RemoveRightSubTree(BTreeNode * bt);
 
void ChangeLeftSubTree(BTreeNode * main, BTreeNode * sub);
 
void ChangeRightSubTree(BTreeNode * main, BTreeNode * sub);

#endif

BinaryTree3.c

#include <stdio.h>
#include <stdlib.h>
#include "BinaryTree3.h"

BTreeNode * MakeBTreeNode(void)
{
	BTreeNode * nd = (BTreeNode*)malloc(sizeof(BTreeNode));

	nd->left = NULL;
	nd->right = NULL;
	return nd;
}

BTData GetData(BTreeNode * bt)
{
	return bt->data;
}

void SetData(BTreeNode * bt, BTData data)
{
	bt->data = data;
}

BTreeNode * GetLeftSubTree(BTreeNode * bt)
{
	return bt->left;
}

BTreeNode * GetRightSubTree(BTreeNode * bt)
{
	return bt->right;
}

void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub)
{
	if(main->left != NULL)
		free(main->left);

	main->left = sub;
}

void MakeRightSubTree(BTreeNode * main, BTreeNode * sub)
{
	if(main->right != NULL)
		free(main->right);

	main->right = sub;
}

void PreorderTraverse(BTreeNode * bt, VisitFuncPtr action)
{
	if(bt == NULL)
		return;

	action(bt->data);
	PreorderTraverse(bt->left, action);
	PreorderTraverse(bt->right, action);
}

void InorderTraverse(BTreeNode * bt, VisitFuncPtr action)
{
	if(bt == NULL)
		return;

	InorderTraverse(bt->left, action);
	action(bt->data);
	InorderTraverse(bt->right, action);
}

void PostorderTraverse(BTreeNode * bt, VisitFuncPtr action)
{
	if(bt == NULL)
		return;

	PostorderTraverse(bt->left, action);
	PostorderTraverse(bt->right, action);
	action(bt->data);
}

BTreeNode * RemoveLeftSubTree(BTreeNode * bt)
{
	BTreeNode * delNode;

	if(bt != NULL) {
		delNode = bt->left;
		bt->left = NULL;
	}
	return delNode;
}

BTreeNode * RemoveRightSubTree(BTreeNode * bt)
{
	BTreeNode * delNode;

	if(bt != NULL) {
		delNode = bt->right;
		bt->right = NULL;
	}
	return delNode;
}

void ChangeLeftSubTree(BTreeNode * main, BTreeNode * sub) 
{
	main->left = sub;
}
 
void ChangeRightSubTree(BTreeNode * main, BTreeNode * sub)
{
	main->right = sub;
}

BinarySearch3.h

#ifndef __BINARY_SEARCH_TREE3_H__
#define __BINARY_SEARCH_TREE3_H__

#include "BinaryTree3.h"

typedef BTData    BSTData;

void BSTMakeAndInit(BTreeNode ** pRoot);

BSTData BSTGetNodeData(BTreeNode * bst);

BTreeNode* BSTInsert(BTreeNode ** pRoot, BSTData data);

BTreeNode * BSTSearch(BTreeNode * bst, BSTData target);

BTreeNode * BSTRemove(BTreeNode ** pRoot, BSTData target);

void BSTShowAll(BTreeNode * bst);

#endif

BinarySearchTree3.c

#include <stdio.h>
#include <stdlib.h>
#include "BinaryTree3.h"
#include "BinarySearchTree3.h"
#include "AVLRebalance.h"

void BSTMakeAndInit(BTreeNode ** pRoot)
{
    *pRoot = NULL;
}

BSTData BSTGetNodeData(BTreeNode * bst)
{
    return GetData(bst);
}

BTreeNode* BSTInsert(BTreeNode ** pRoot, BSTData data)
{
    if(*pRoot == NULL)
    {
        *pRoot = MakeBTreeNode();
        SetData(*pRoot, data);
    }
    else if(data < GetData(*pRoot))
    {
        BSTInsert(&((*pRoot)->left), data);
        *pRoot = Rebalance(pRoot);
    }
    else if(data > GetData(*pRoot))
    {
        BSTInsert(&((*pRoot)->right), data);
        *pRoot = Rebalance(pRoot);
    }
    else
    {
        return NULL; // 키의 중복은 허락하지 않는다( data == GetData(*pRoot)
    }
    return *pRoot;
}

BTreeNode * BSTSearch(BTreeNode * bst, BSTData target)
{
    BTreeNode * cNode = bst;    // current node
    BSTData cd;    // current data

    while(cNode != NULL)
    {
        cd = GetData(cNode);

        if(target == cd)
            return cNode;
        else if(target < cd)
            cNode = GetLeftSubTree(cNode);
        else
            cNode = GetRightSubTree(cNode);
    }

    return NULL;
}

BTreeNode * BSTRemove(BTreeNode ** pRoot, BSTData target)
{

    BTreeNode * pVRoot = MakeBTreeNode();

    BTreeNode * pNode = pVRoot;    // parent node
    BTreeNode * cNode = *pRoot;    // current node
    BTreeNode * dNode;    // delete node

    ChangeRightSubTree(pVRoot, *pRoot);
    
    while(cNode != NULL && GetData(cNode) != target)
    {
        pNode = cNode;

        if(target < GetData(cNode))
            cNode = GetLeftSubTree(cNode);
        else
            cNode = GetRightSubTree(cNode);
    }

    if(cNode == NULL)
        return NULL;

    dNode = cNode;

    if(GetLeftSubTree(dNode) == NULL && GetRightSubTree(dNode) == NULL)
    {
        if(GetLeftSubTree(pNode) == dNode)
            RemoveLeftSubTree(pNode);
        else
            RemoveRightSubTree(pNode);
    }

    else if(GetLeftSubTree(dNode) == NULL || GetRightSubTree(dNode) == NULL)
    {
        BTreeNode * dcNode;    // delete node

        if(GetLeftSubTree(dNode) != NULL)
            dcNode = GetLeftSubTree(dNode);
        else
            dcNode = GetRightSubTree(dNode);

        if(GetLeftSubTree(pNode) == dNode)
            ChangeLeftSubTree(pNode, dcNode);
        else
            ChangeRightSubTree(pNode, dcNode);
    }

    else
    {
        BTreeNode * mNode = GetRightSubTree(dNode);    // mininum node
        BTreeNode * mpNode = dNode;    // mininum node
        int delData;

        while(GetLeftSubTree(mNode) != NULL)
        {
            mpNode = mNode;
            mNode = GetLeftSubTree(mNode);
        }
        
        delData = GetData(dNode);
        SetData(dNode, GetData(mNode));

        if(GetLeftSubTree(mpNode) == mNode)
            ChangeLeftSubTree(mpNode, GetRightSubTree(mNode));
        else
            ChangeRightSubTree(mpNode, GetRightSubTree(mNode));

        dNode = mNode;
        SetData(dNode, delData);
    }

    if(GetRightSubTree(pVRoot) != *pRoot)
        *pRoot = GetRightSubTree(pVRoot);

    free(pVRoot);

    *pRoot = Rebalance(pRoot);
    return dNode;
}

void ShowIntData(int data)
{
    printf("%d ", data);
}

void BSTShowAll(BTreeNode * bst)
{
    InorderTraverse(bst, ShowIntData);
}

대단히 수고했다!
다음 포스트 부터는 테이블과 해쉬를 배워보자

서희찬

부족한 실력을 엉덩이 힘으로 채워나가는 개발자 서희찬입니다 :)

이전 포스트

[자료구조]탐색 2 (12-2-3) Rebalance 함수

다음 포스트