데이터 전처리

• 2022년 12월 개인적으로 진행했던 토이프로젝트를 정리하여 블로그에 재업로드합니다.

4. Data Preprocessing

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split

1) NA Imputation

• NA값은 자유투 성공률을 의미하는 feature인 FT%_H 와 FT%_A에 존재하며, 자유투 시도가 없어 성공률이 NA인 경우입니다.

• 실제 자유투를 시도했을 때의 성공률과 구분하기 위해 NA를 -1로 대체합니다.

basket['FT%_H'][basket['FT%_H'].isna()]=-1.0
basket['FT%_A'][basket['FT%_A'].isna()]=-1.0

basket.isna().sum()

2) Feature Engineering

(1) MP 변수 삭제

앞서 3-2) Features 에서 언급했듯, MP 변수는 총 출전시간을 의미하는 feature로 모든 경기에서 각팀이 120으로 일정한 값을 가집니다. 따라서 해당 feature를 삭제합니다.

basket=basket.drop(['MP_H','MP_A'],axis=1)
basket.shape

(2761, 39)

(2) 2점 야투에 대한 변수 생성 및 전체 야투 변수 삭제

기존의 FG, FGA, FG% feature의 경우 2점 야투와 3점 야투를 모두 포함하는 feature입니다. 그런데 3점 야투에 대한 feature가 3P, 3PA, 3P%로 따로 존재하는 만큼, 전체 야투에 대한 feature와 3점 야투에 대한 feature를 이용하여 2점 야투에 대한 feature 2P, 2PA, 2P%를 생성합니다.

* 2P = FG-3P
* 2PA = FGA-3PA
* 2P% = 2P/2PA

2점 야투에 대한 feature들을 생성하고 나면 전체 야투에 대한 feature는 3점 야투에 대한 feature와 2점 야투에 대한 feature로 충분히 설명되므로 전체 야투에 대한 feature FG, FGA, FG%를 삭제합니다.

basket['2P_H']=basket['FG_H']-basket['3P_H']
basket['2P_A']=basket['FG_A']-basket['3P_A']
basket['2PA_H']=basket['FGA_H']-basket['3PA_H']
basket['2PA_A']=basket['FGA_A']-basket['3PA_A']
basket['2P%_H']=basket['2P_H']/basket['2PA_H']
basket['2P%_A']=basket['2P_A']-basket['2PA_A']

basket=basket.drop(['FG_H','FG_A','FGA_H','FGA_A','FG%_H','FG%_A'],axis=1)

(3) ORB, DRB feature 삭제

리바운드는 공격리바운드(ORB)인지 수비리바운드(DRB)인지와 관계 없이 공격권을 한번 더 가져오는 같은 역할을 한다는 점에서 총 리바운드 횟수인 TRB만 사용합니다.

basket=basket.drop(['ORB_H','ORB_A','DRB_H','DRB_A'],axis=1)

(4) Team feature 삭제

다음과 같은 이유로 각 팀을 나타내는 범주형 feature인 'Team_H'와 'Team_A'를 삭제합니다.

• 현재 basket 데이터 프레임의 feature가 매우 많은 편이고 전체 팀 수가 30개나 되기 때문에 one-hot encoding을 하기에는 무리가 있다고 판단
• 본 프로젝트를 통해 구현하고자 하는 승부 예측 모델은 팀이 어떤 팀인지보다는 전반전의 세부 스탯을 중심으로 예측을 진행하는 것이 목적임

basket=basket.drop(['Team_H','Team_A'],axis=1)

3) Log Transformation

right skewed된 형태의 분포를 가지는 BLK_H, BLK_A 변수를 log transformation 하여 정규성을 높여줍니다.

basket["BLK_H"] = np.log1p(basket["BLK_H"])
basket["BLK_A"] = np.log1p(basket["BLK_A"])

fig, ax = plt.subplots(ncols=2, nrows=1, figsize=(20,1*5))

sns.kdeplot(x='BLK_H', data=basket, hue="HomeWin",fill=True, ax=ax[0])
sns.kdeplot(x='BLK_A', data=basket, hue="HomeWin",fill=True,ax=ax[1])

4) Square Transformation

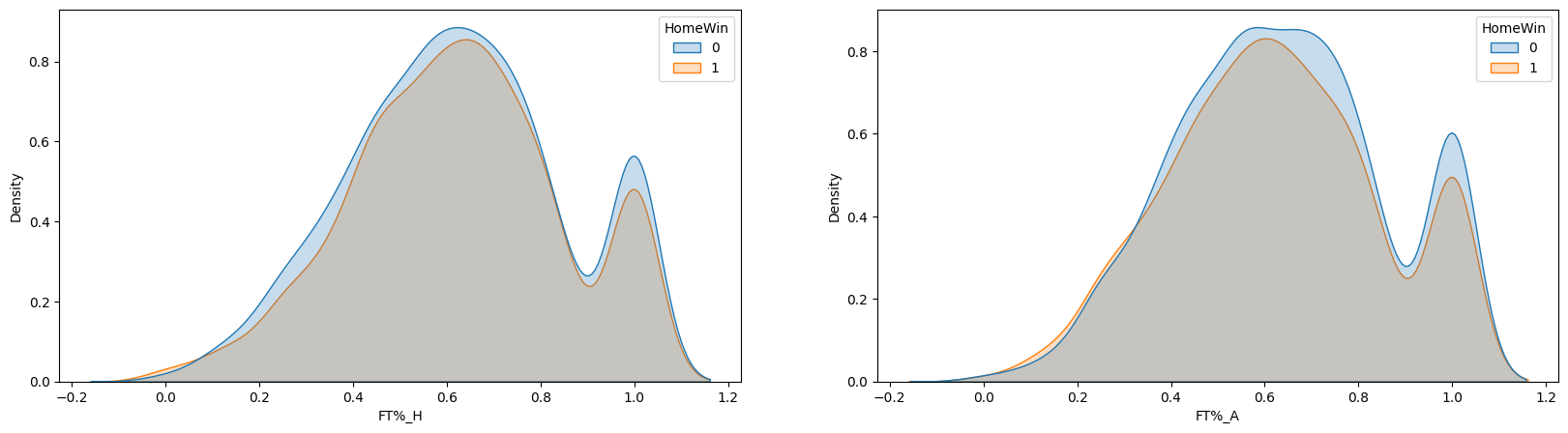
left skewed 된 feature 인 'FT%_H'와 'FT%_A'를 square transformation을 통해 skweness를 완화시킵니다.

• reference : https://medium.com/@TheDataGyan/day-8-data-transformation-skewness-normalization-and-much-more-4c144d370e55

basket['FT%_H']=(basket['FT%_H'])**2
basket['FT%_A']=(basket['FT%_A'])**2

fig, ax = plt.subplots(ncols=2, nrows=1, figsize=(20,1*5))

sns.kdeplot(x='FT%_H', data=basket, hue="HomeWin",fill=True,ax=ax[0])
sns.kdeplot(x='FT%_A', data=basket, hue="HomeWin",fill=True,ax=ax[1])

5) Label 분리, Train/Test Dataset 분리

모델 훈련에 사용하기 위해 label feature인 'HomeWin'을 분리하고, 전체 데이터셋을 Train set과 Test set으로 분리합니다.

전체 데이터의 25%를 test 데이터로 사용합니다.

y=basket['HomeWin']
X=basket.drop(['HomeWin'],axis=1)

X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.25)

6) PCA

X_train.shape

(2070, 32)

feature의 수가 32개로 많은 편이기 때문에 차원을 축소하여 모델 적합에 사용할 수 있도록 PCA를 적용한 데이터셋을 생성합니다. PCA를 적용할 것인지의 여부는 이후 모델을 적합해 보고 실험적으로 결정합니다.

principal component의 갯수를 결정하기 위해 X_train에 대해 pca를 진행한 후 각 principal component가 설명한는 분산의 양을 살펴보겠습니다.

• reference : https://plotly.com/python/pca-visualization/

pca = PCA()
pca.fit(X_train)
exp_var_cumul = np.cumsum(pca.explained_variance_ratio_)

px.area(
    x=range(1, exp_var_cumul.shape[0] + 1),
    y=exp_var_cumul,
    labels={"x": "# Components", "y": "Explained Variance"}
)

12개의 principal component로 전체 분산의 95%를 설명할 수 있네요. 이후 사용하기 위해 n_component=12 로 차원축소한 데이터셋을 생성해두겠습니다.

pca=PCA(n_components=12)
X_train_pca=pca.fit_transform(X_train)
X_test_pca=pca.transform(X_test)