그래프 어텐션 신경망 (Graph Attention Network, GAT)

이전 포스팅 복습

• 학습의 결과로 임베딩 자체가 아닌 인코더를 얻는 귀납식 방법의 대표적 예시가 GNN(그래프 신경망)으로.
  이는 이웃 노드들의 정보를 집계하는 과정을 반복하여 임베딩을 얻었다
• 그리고 집계함수의 형태에 따라 GNN, GCN, GraphSAGE 등으로 구분이 된다
• 그래프 신경망은 비지도, 지도 모두 가능한데
  비지도 학습에서는 노드간 유사도를 '보존'하는 것을 목표로 하고
  지도 학습에서는 후속 과제의 손실함수를 이용해 종단종 학습(End-to-End)을 한다
• 학습된 신경망을 적용하여 학습에 사용되지 않은 노드, 학습 이후에 추가된 노드, 새로운 그래프의 노드의 임베딩을 얻을 수 있다

그래프 신경망에서의 어텐션

기존 그래프 신경망의 한계

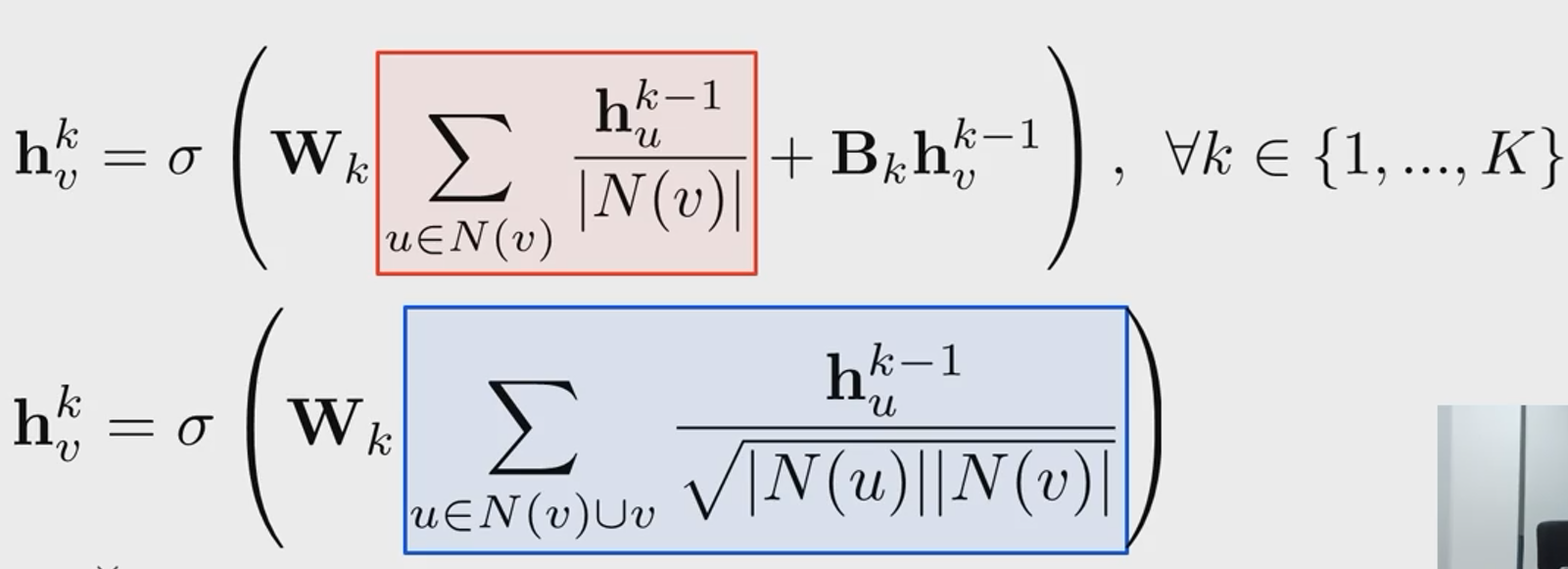
• 기본 GNN에서는 이웃들의 정보들 동일한 가중치로 평균을 낸다
• GCN에서도 역시 단순히 연결성을 고려한 가중치로 평균을 낸다
  => 즉, 기존 그래프 신경망 방법은 이웃별로 미치는 영향을 동일하게 취급을 한다

그래프 어텐션 신경망(Graph Attention Network, GAT)

GAT에서는 노드 간의 가중치도 학습의 대상이 된다
실제 그래프에서는 이웃 별로 미치는 영향이 다를 수 있음을 고려하여 가중치를 학습하기 위해 Self-Attention을 사용한다

노드 간의 가중치는 다음과 같은 과정으로 산출된다

이 때, 가중치를 하나만 사용할필요는 없다
여러개의 Attention 학습의 결과를 concat 하여 사용할 수 있으며, 이를 '멀티헤드 어텐션(Mutli-head Attention)'이라 부른다

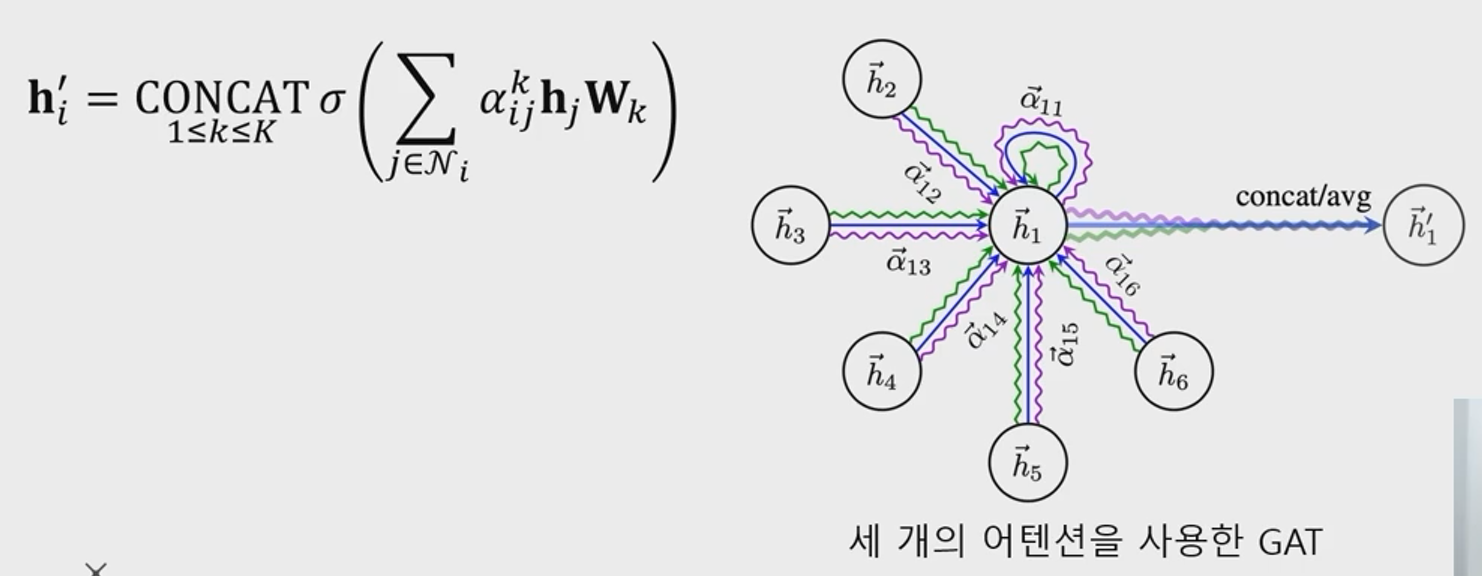
가중치 k 개를 연결하여 최종 임베딩을 산출하는 그림이다

그래프 표현 학습 (그래프 임베딩)

그래프 표현 학습, 혹은 그래프 임베딩이란 그래프 전체를 벡터의 형태로 표현하는 것을 의미한다

그리고 그래프 풀링이란 노드 임베딩들로부터 그래프 임베딩을 얻는 과정이다
평균 등의 단순한 방법보다 그래프 구조를 고려한 방법을 사용하는 경우 더 높은 성능을 얻는다고 한다

지나친 획일화 문제

지나친 획일화(Over-smoothing)문제란 그래프 신경망의 층의 수가 증가하면서 노드의 임베딩이 서로 유사해지는 현상을 의미

잔차항(Residual)을 넣는 것, 즉 이전 층의 임베딩을 한번 더 더해주는것만으로는 효과가 제한적이다
이 문제의 대응으로 JK 네트워크는 마지막 층이 임베딩 뿐 아니라, 모든 층의 임베딩을 함께 사용한다
AFPNP는 0번째 층을 제외하고는 신경망 없이 집계 함수를 단순화하였다