인공지능 분야를 공부하다보면 선형대수학, 신경망, 데이터 전후처리 등등 알아야할 사항이 너무나도 많다. 작업을 하다보면 제대로 알지못하면서 그냥 넘어가는 부분이 많았던 것 같다.
'기본이지만 쉽게 넘어갈법한, 그리고 중요한' 개념들에 대해 포스팅해본다. 중간중간 계속 수정하여 내용을 더해갈 예정이다
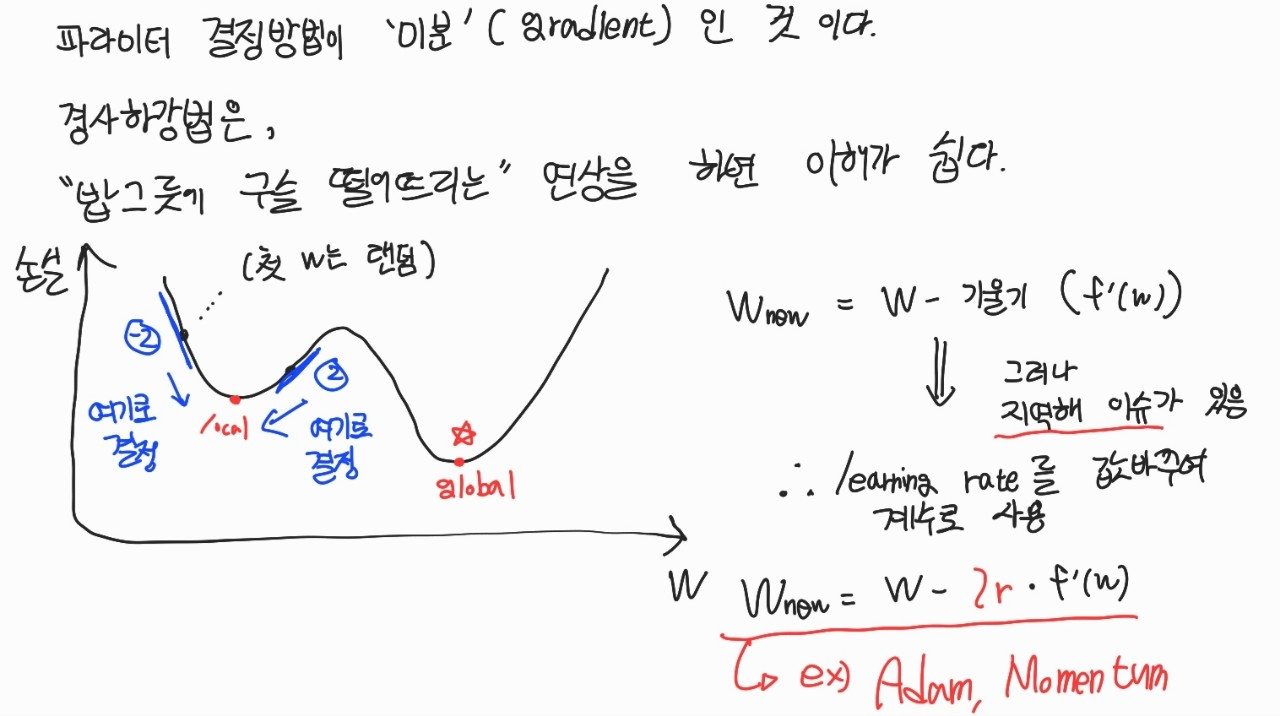
경사하강법 (Gradient Descent)
목적함수 정의 후 오차값을 최소화하고자 할 때, 모델의 파라미터를 정하는 과정에서 사용되는 기법이다.
경사하강법에 대해서 직접 그림으로 표현해보았다
활성화 함수 (Activation Function)
딥러닝에서 입력값으로 받은 값을 특정 함수에 넣어 조치한 후, 다음 층으로 전달하기 직전 사용하는 함수를 활성화 함수라고 한다. 이 때 활성화 함수는 비선형 함수만을 사용한다. 활성화 함수가 선형이면 비선형 문제를 해결할 수 없기 때문이다. 선형 함수를 사용하면 신경망층의 층을 깊게 쌓는 것이 의미가 없어진다.
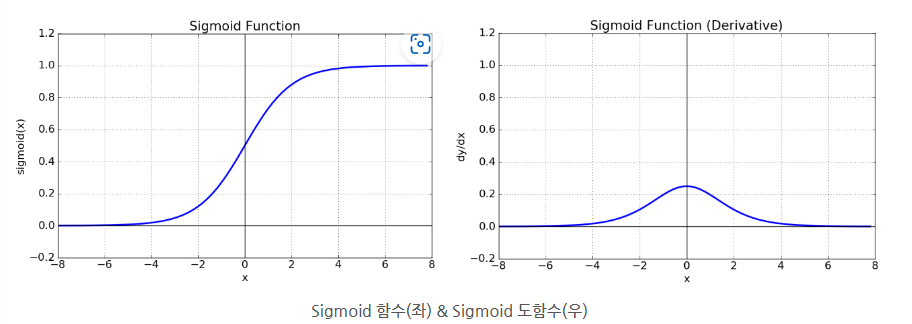
1. Sigmoid, 그리고 기울기 소실
1/(1 + e^(-x)). 0 ~ 1 로 값을 찌부시켜 주는 역할이다.
하지만 딥러닝에서 학습을 위해 오차역전파를 진행하는 과정에서 활성화 함수의 미분 값을 연쇄적으로 곱하는 과정이 포함되는데, 시그모이드의 경우 기울기값이 최대 0.25기 때문에 1보다 작은 값을 계속 곱하면 0에 수렴하게 된다.
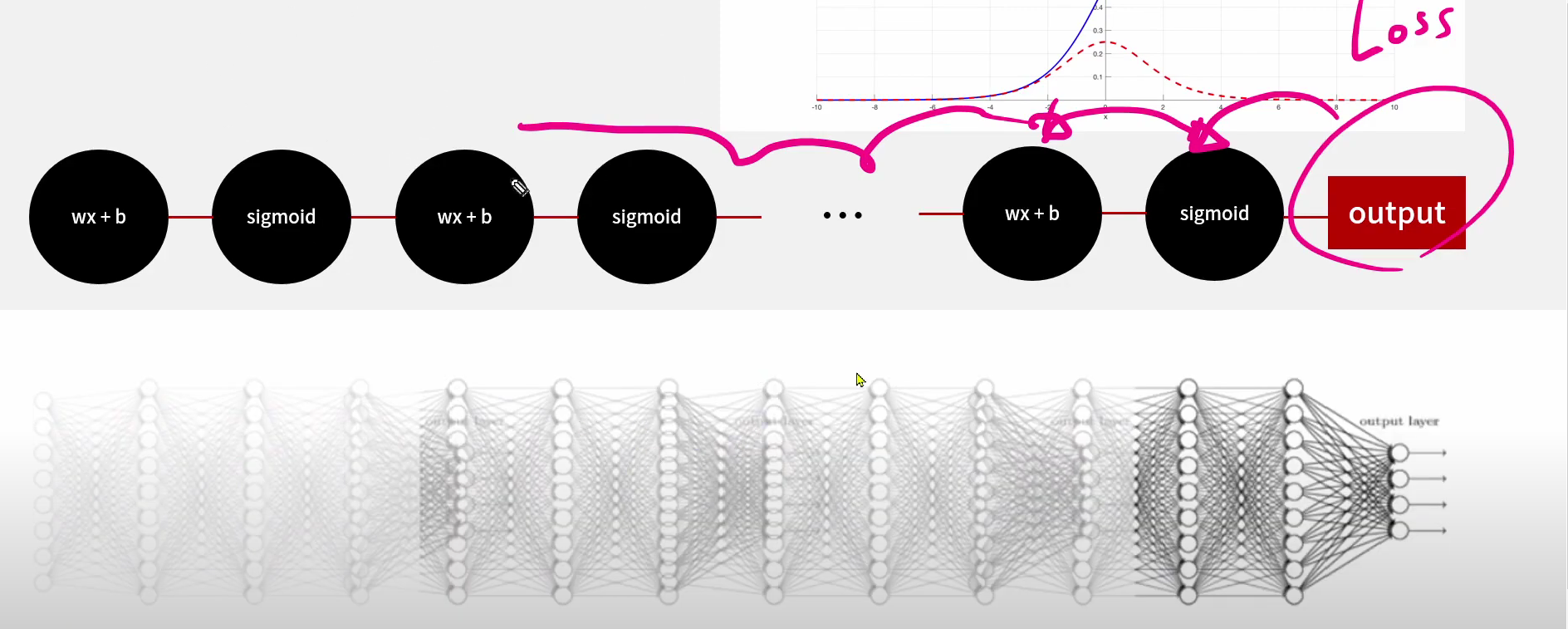
(이미지 출처 : 유튜브 테디노트)
층이 깊어질수록 기울기 소실 (미분값 0 : 즉 업데이트가 일어나지 않음) 현상이 심해진다. 위의 그림처럼 loss값을 역으로 전달하는 과정에서 최근꺼는 업데이트를 해줄수 있지만 멀어질수록 0으로 수렴되는 값을 전달해주기 때문에 업데이트를 해야해도 할수도 없는 상황인 것이다.
2. tanh
sigmoid와 형태가 거의 유사하다. 기존이 0~1로 찌부라면, 이 녀석은 -1~1 범위로 scaling해준다
sigmoid 함수의 중심값이 0이 아닌 0.5라서 학습이 느린 문제가 있었는데 tanh는 중심값을 0으로 옮겨서 느려지는 문제를 해결했다. 하지만 기울기 소실 문제는 여전히 남아있다
3. Relu
Relu는 Rectified Linear Unit 의 준말로, 본래 네이밍을 생각하면 함수의 모양을 연상하기 쉽다. 가장 많이 사용되는 활성화 함수 중 하나로, 기울기 소실의 문제를 해결하기 위한 함수이다.
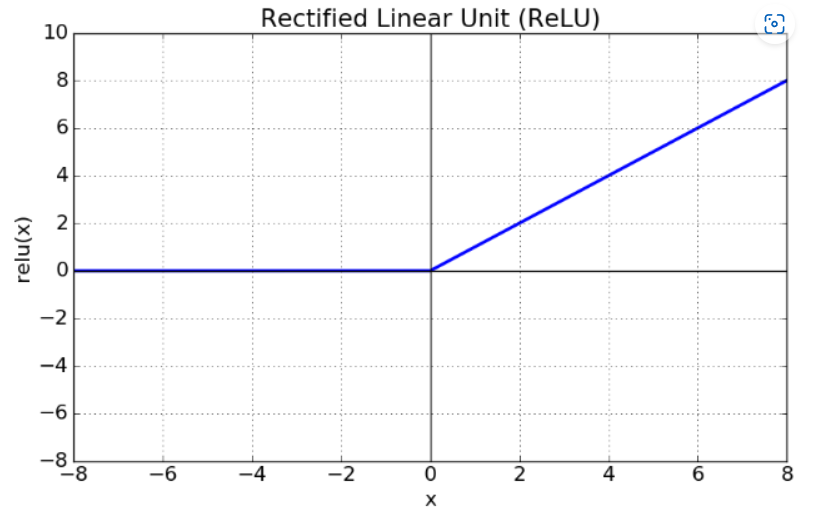
x가 0보다 크면 기울기가 1인 직선, 0보다 작으면 함수 값이 0이 된다. 0보다 작은 값들에서 뉴런이 죽을 수 있는 단점을 야기하지만 학습이 기존보다 빠르고 연산 cost도 적으며 구현도 매우 간단하다는 특징이 있다.
LSTM, GRU
위에서 서술한 Gradient Descent, 활성화 함수의 내용을 이용해서 RNN에서의 장기의존성 문제를 해결한 LSTM, GRU에 대해서 작성한다. 이는 문장번역과 GNN 등 다양하게 사용된다.
- reference : https://wooono.tistory.com/242
1. RNN
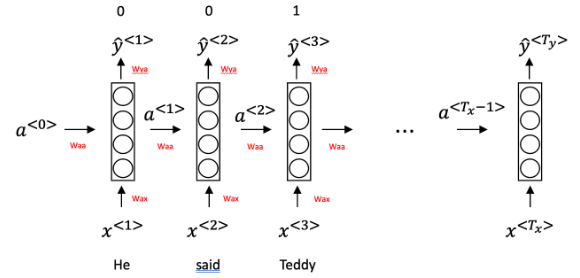
- RNN의 기본 구조는 위 그림과 같다. 기존의 CNN처럼 앞으로만 진행하는 것이 아닌, 이전 연산을 활용한다는 점이 특징이다.
- RNN 관련하여서는 예전에 포스팅 한적이 있다. [여기:https://velog.io/@seojeongbin/RNN]에서 확인할 수 있다
- 그러나 시퀀스가 길어지면 초반부의 영향력이 감소한다는 문제점이 있다 (Vanishing graients)
이를 해결하기 위해, LSTM(Long Short Term Memory)가 제안됐다.
2. LSTM (Long Short Term Memory)
이전 정보를 그냥 갖고오는게 아니라 무엇을 기억하고 잊을지를 관리하는 Cell State가 핵심인 구조이다
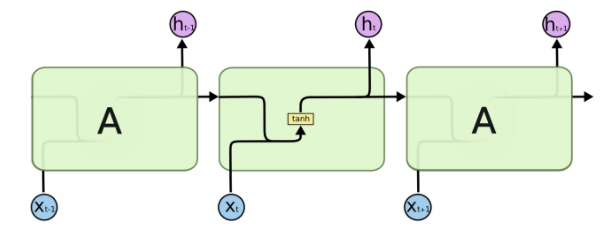
기존 RNN의 구조가 위와 같다면 LSTM의 구조는 아래 그림과 같다
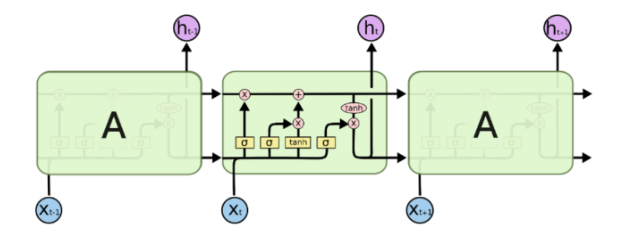
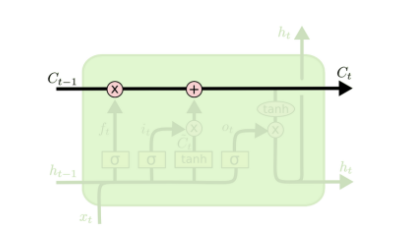
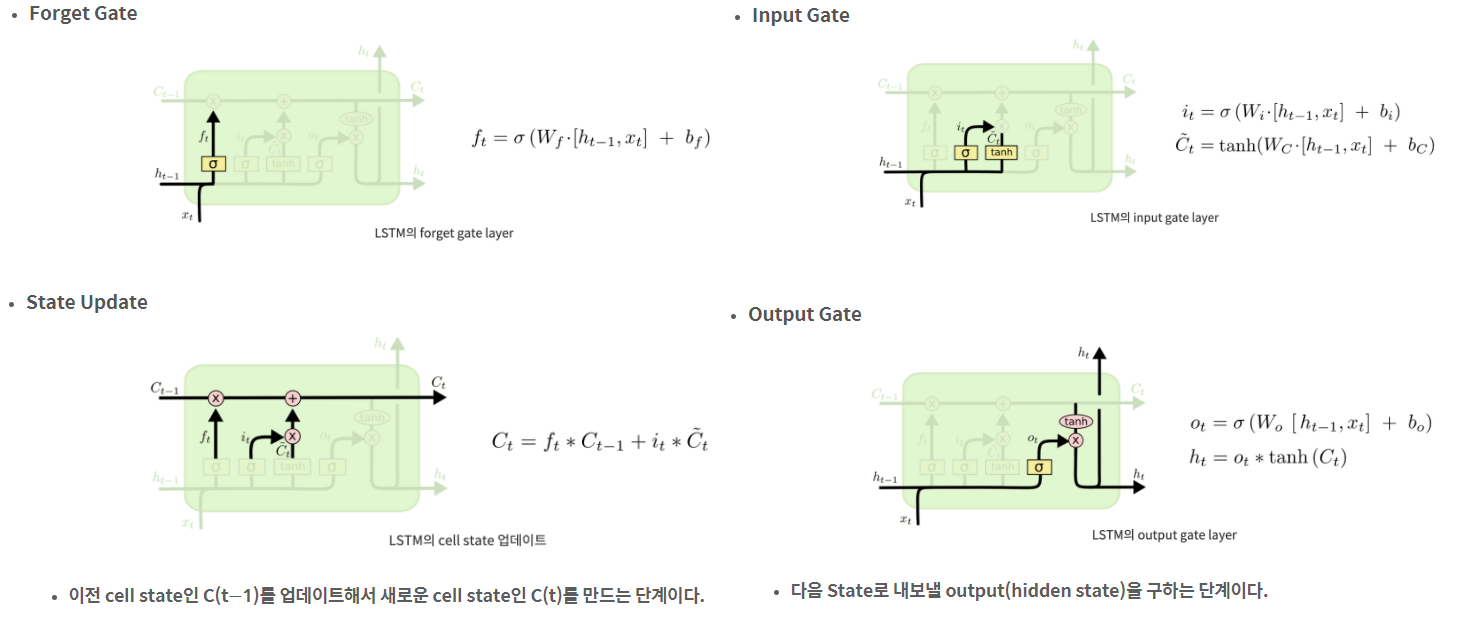
- LSTM의 핵심인 Cell State는 모듈 그림에서 수평으로 그어진 윗 선에 해당한다
- 컨베이어 벨트와 같아서 State가 꽤 오래 경과하더라도 Gradient가 잘 전파된다
- Cell State는 Gate라 불리는 구조에 의해 정보가 추가되거나 제거된다
- Gate : training을 통해 어떤 정보를 유지하고 버릴지 학습한다
- forget gate, input gate, output gate : 과거 정보를 잊기위한, 현재 정보를 기억하기 위한, 최종결과를 내보내기 위한
- 모든 Gate는 활성화함수롤 Sigmoid를 사용하고 출력 범위 0~1에 따라 넘길 값을 정한다
3. GRU (Gated Recurrent Unit)
LSTM이 경량화된 버전이다. 구조는 가벼워졌지만 성능감소가 미미하여 개발된이후로 많이 쓰인다.
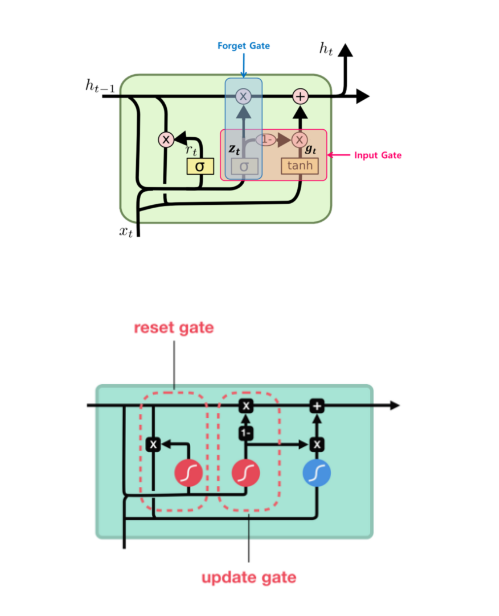
- 구조는 위와 같으며, 기존 LSTM에서 Cell State와 Hidden State가 그냥 하나의 Hidden State로 통합되었단 것이 특징이다
- Gate도 3개가 아닌 2개이다 (Reset, Update : Output Gate가 없다)
오토인코더 (AutoEncoder, AE)
최신기술에 근간이되는 오토인코더에 대해 작성한다. 오토인코더는 비지도학습이다. 보통 차원축소에 유용하게 사용된다
- 정답에 해당하는 레이블이 없는 비지도학습의 일종이다
- 무언가를 예측, 혹은 분류하는 목적이 아닌 차원축소(압축의 느낌)의 목적으로 보통 사용된다
- 인코더(앞부분)은 인풋으로 받은 크기(차원)을 점점 줄어들게하고 디코더(뒷부분)은 인코더의 정반대 구성으로서 인풋과 동일한 결과를 출력하는 것을 목표로 한다
- 클라우드 센서 등에 올릴 때 더 작은 사이즈로 넣어줄 수 있다 (이게 알집원리다)
- 코드구현을 해보면 대칭구조인 점이 특징이다
- 이때 계층을 지날수록 차원이 줄어든다는 것을 주어진 정보를 압축하며 불필요한 정보를 버리는 셈이다.
- 따라서 덜 중요한 잡음을 제거하는 목적으로도 사용을 한다
- 구현은 별거없고 대칭구조인 점이 특징이다