딥러닝 기초 : 다층 레이어 사용이유와 오차역전파 관련

놓치기 쉬운 인공지능 개념
위 링크와 같이 본 포스팅 내용을 참고하면 도움이 될 것 같다
해당 링크에서 작성한 내용보다 좀 더 기초적인, 추가적인 내용을 작성한다

0. 딥러닝 이란?

• 딥러닝은 데이터를 입력받으면 설정된 목표 TASK를 수행한다
  • 이 때 설정된 목표를 1.파라미터(가중치) 2.목적함수 를 통해 수행하게 된다
  • 어떤 파라미터를 사용하느냐에 따라 LOSS가 달라진다

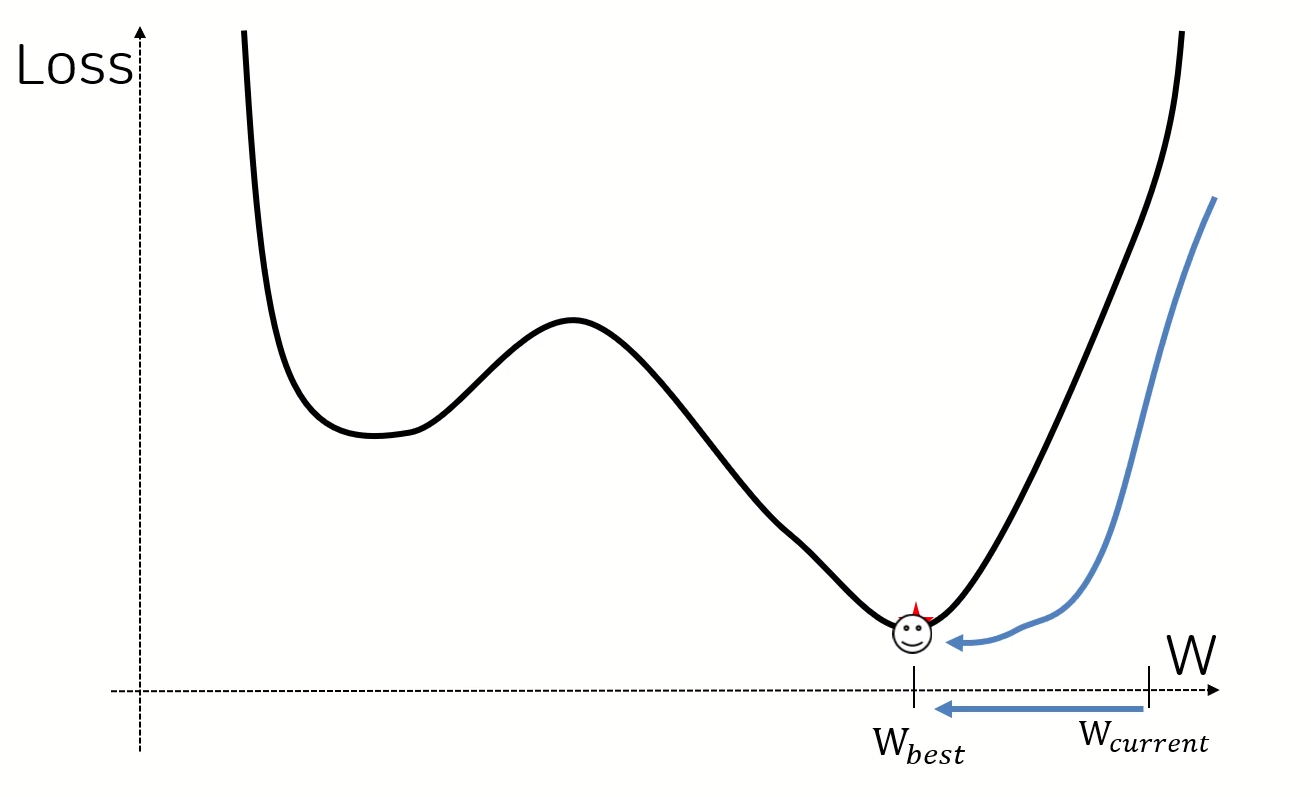
즉 목적함수에 대한 오차에 대해 BEST LOSS, BEST PARAMTER를 찾는게 딥러닝의 학습목표 인 것이다

• 이를 도와주는게 Optimizer이다 (현재의 w 위치로부터 Best w위치를 찾아가는 것)
  • 어디에 w best가 있으며, w loss fn은 어떻게 생겼는지..

1. 퍼셉트론과 MLP

퍼셉트론이 곧 단층 레이어이다. 하지만 단층 레이어일때의 문제점이 풀어야 하는 상황이 비선형인 경우 해결할 수 없다는 점이다.

• 이를 hidden layer 를 추가한 형태인 다층 레이어로 해결할 수 있다. 아래 그림에서 표현된대로 일반 퍼셉트론으로 XOR을 풀 수 없는 것을 and와 or 레이어를 동시에 사용함으로써 풀 수 있듯이 말이다.

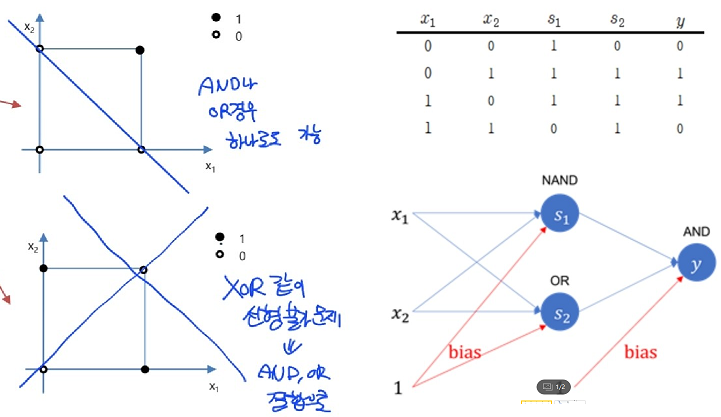
(기존 선형으로는 해결못했던 XOR문제를 NAND(AND의 부정)와 OR의 결합으로 해결한 모습 : 우측상단 표 참고)

=> 하지만 '활성화 함수'가 없이 층만 쌓으면 MLP도 결국 퍼셉트론의 형태인 선형 결합 꼴로 표현된다. aw1 + bw2로 식 정리가 되어버림

결국 딥러닝을 통해 비선형 문제를 해결하기 위해선,

• hidden layer를 통해 층을 쌓아야 한다
• hidden layer 이용 시 활성화 함수를 꼭 사용해야 한다 (사용하지 않으면 단층 퍼셉트론과 다른게 없음!)

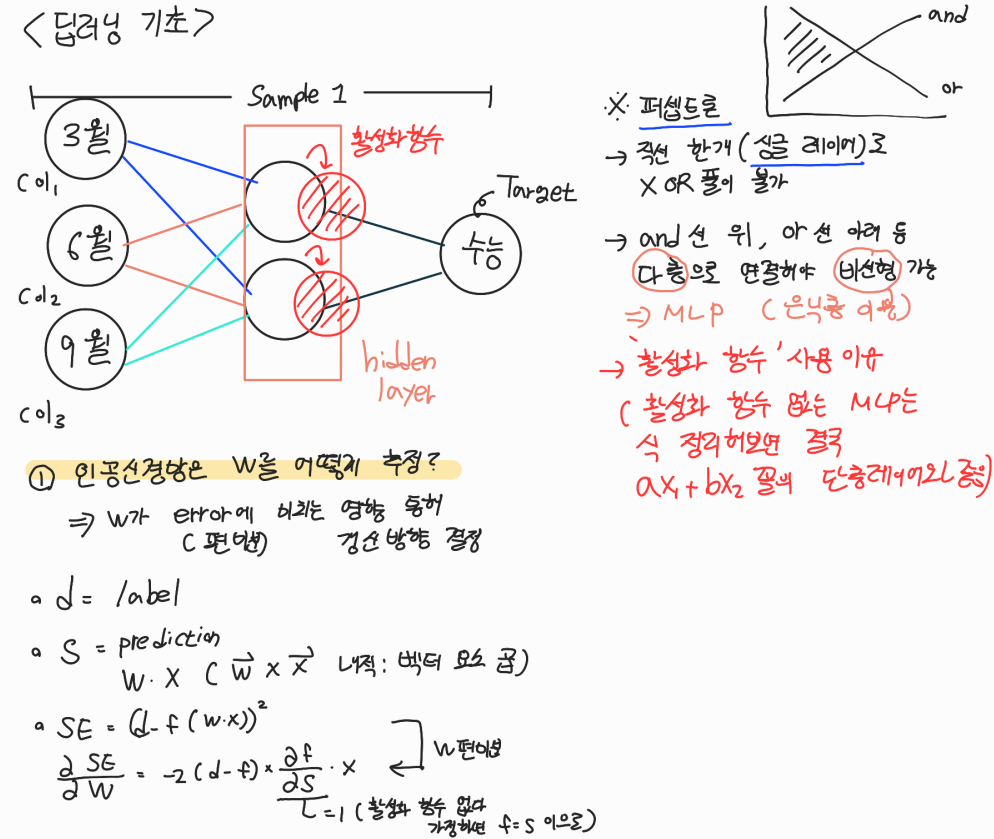
2. 딥러닝에서 가중치를 추정하는 원리

• 경사하강법을 통해 w를 구한다. w가 error에 미치는 영향을 통해 매 순간 update하는 방향을 정하는 것이다
• 이에 대해 수식으로 위에서 정리를 하여보았다. 밥그릇에 구슬을 떨어지는 것으로 연상해보면 이해하기 쉽다
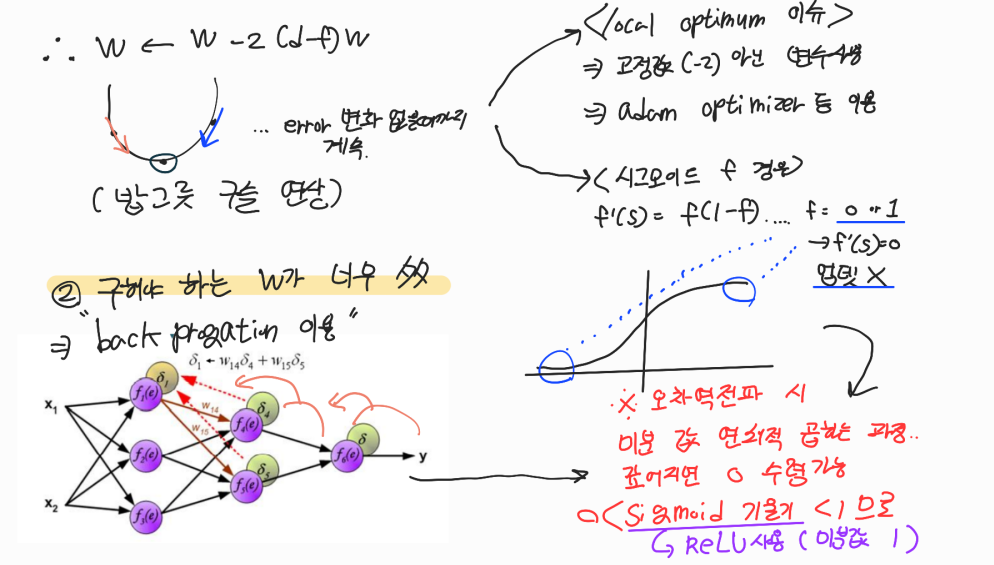
• 이 때 global 해가 아닌 local 해를 구하는 문제를 극복하고자 adam optimizer 등을 사용하는 것이다

3. backprogation과 기울기 소실(폭발)

• 구해야 하는 w가 엄청 많기때문에 뒷부분의 오차를 앞부분에 활용하는 식으로 연쇄적으로 활용하는 backpropagation(오차역전파) 방법을 사용한다
• 이 때 미분 값을 연쇄적으로 곱하게 되는데, 시그모이드 처럼 기울기 값이 1 미만인경우 (시그모이드는 기울기의 최대값이 0.25라서 층이 깊어지면 필연적으로 이런 문제가 발생하게 된다) 0에 수렴하여 w update가 일어나지 않게된다
  • 층이 깊어지지 않더라도 시그모이드의 미분 형태는 f(1-f)라서 양 끝점 0,1이 되면 0에 가까워진다 * 즉, vanishing gradient랑 무관하게 이런 문제 발생 가능
• 이를 다른 활성화함수 형태인 ReLU로 해결할 수 있다 이는 max(0,x) 형태라 양수영역에서 기울기가 1이라 이런 문제를 극복할 수 있다.

4. 보완점 (개인메모용)

• 오차역전파 수식부분 & 시그모이드 단점부분 책 참고해서 수식 단위로 이해해보기.
• 확률적 경사하강법과 Adam 관련 영상