시계열 분석

1. 시계열 이란?

• 값이 시간에 흐름에 따라 축척된 데이터를 의미
  • 그렇기 때문에 일반 데이터프레임처럼 train, validation Divide 경우 랜덤 split하면 안됨! (시계열 정보가 없어지므로)
  • Train은 앞부분 데이터, Validation은 뒷부분 데이터 이런식으로 나눔
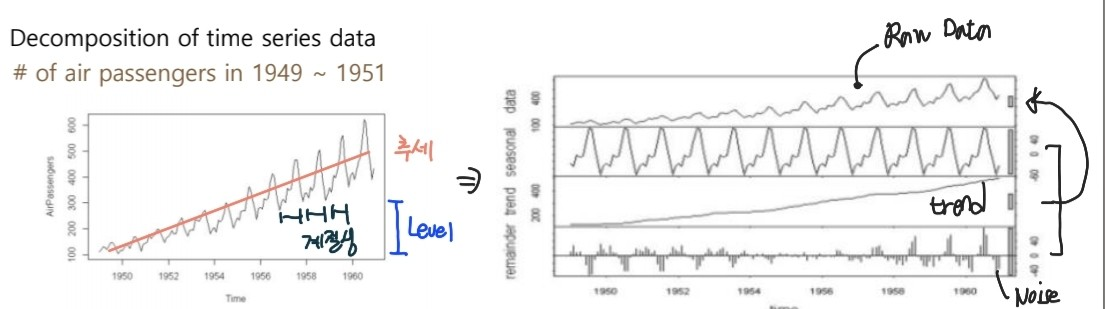
• 다음과 같은 구성요소를 갖고 있음
  • Level : 평균
  • Trend : 추세
  • Seasonality : 계절성 (주기성)
  • Noise : 기타 변동 (시계열 데이터에서 위에 세개를 제외하고 남는 것)
    

2. 회귀관점에서의 시계열

2-1. Regression

• 일반 선형 회귀로 접근하는 경우, Seasonality를 반영할 수 없음
• 비선형 trend도 반영할 수 없음

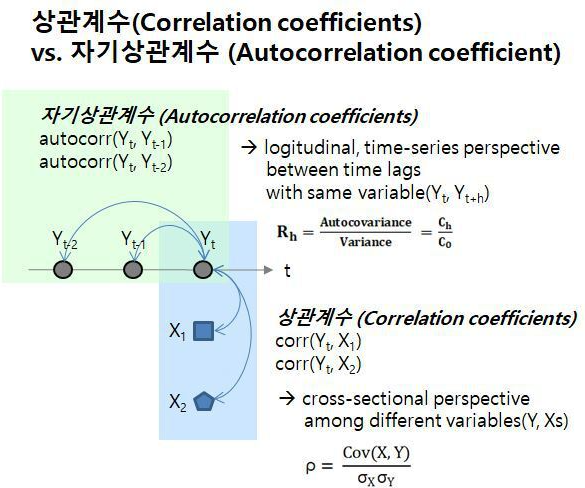
2-2. Autocorrelation

변수끼리 영향받는 게 아니라, 하나의 칼럼에서 자기들끼리 영향 받는 것을 Autocorrelation (자기상관) 이라 함

이미지 출처 바로가기

• 이때 직전 한칸 데이터만큼 영향받는것을 lag = 1 이라하며, 'stickiness'라 한다 (끈적끈적)
• lag > 1 인 경우를 seasonal pattern 이라 보는 것이다

2-2-1. AR model

• AutoRegression model로서, 직전 데이터들이 현재 데이터에 영향 미치는것을 Regression으로 표현한 것이다
• AR(1) : 직전 데이터 하나가 현재 값에 영향 미친다 : Y(t) = a*Y(t-1) + C + Error
• AR(2) : 직전 데이터 두개가 현재 값에 영향 미친다 : Y(t) = aY(t-1) + bY(t-2) + C + Error
  • Error = u*e(t)

2-2-2. MA

• Moving Average
• 직전의 에러에만 영향을 받는다는 모델
• MA(1) : Y(t) = ae(t-1) + C + Error / Error = ue(t)
  • 기존의 경우 error는 보통 서로 독립이지만, 시계열에서는 독립이라 볼 수 없음. error도 변수로 사용
  • 관련 설명

2-3. ARIMA

2-3-1. ARMA

• AR model + MA model => ARMA model 이 된다

2-3-2. ARIMA

• ARMA 같은경우에는 Correleation만 사용한다 : trend 고려 불가

  • 변수간 상관관계 : x가 큰 값을 가지면, y도 큰 값을 갖는 경향
  • Y_t, Y_t-1 의 관계만 본다는 것

• ARIMA의 경우 Co-integration을 사용한다 : trend 고려 가능

  • x가 증가하면, y도 증가하는 경향이 있다
  • (Y_t, Y_t-1) 와 (Y_t-1, Y_t-2)의 상관관계가 되는 것
    => ARIMA를 통해 증감패턴이 있는 경우까지 고려할 수 있어, stationarity한 경우 외에도(trend 없는 시계열) trend까지 고려하여 예측할 수 있게 됨 / stationarity(: 정상성 -> 분포가 비슷하게 일정한 시계열 의미)
    

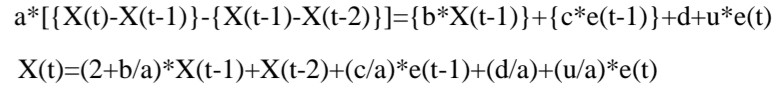
3. 신경망 관점의 시계열

3-1. RNN

• 초기 영향력이 감소하는 문제가 있다 = > LSTM 이용하게 됨

3-2. LSTM

• 특화 gate를 사용하여 장기 기억할 수 있도록 풀이한다

RNN과 LSTM 관련해서는 이전에 몇번 포스팅 하였다