레드-블랙트리의 삽입방법

Intro

• 레드-블랙트리의 특성을 유지하기위해 어떤 연산을 해야할까?

레드-블랙 트리의 연산

• 탐색: 이진 탐색트리와 같음
  • 단, O(logN)을 보장함!
• 삽입과 삭제
  • 일단 삽입 혹은 삭제실행(특성이 망가질 수 있음)
  • 그 후, 망가진 특성을 고치기위해 트리의 구조를 재배치(회전)혹은 노드 색을 바꿈
  • 완벽하진 않으나 탐색시간 O(logN)을 보장하는정도의 균형!
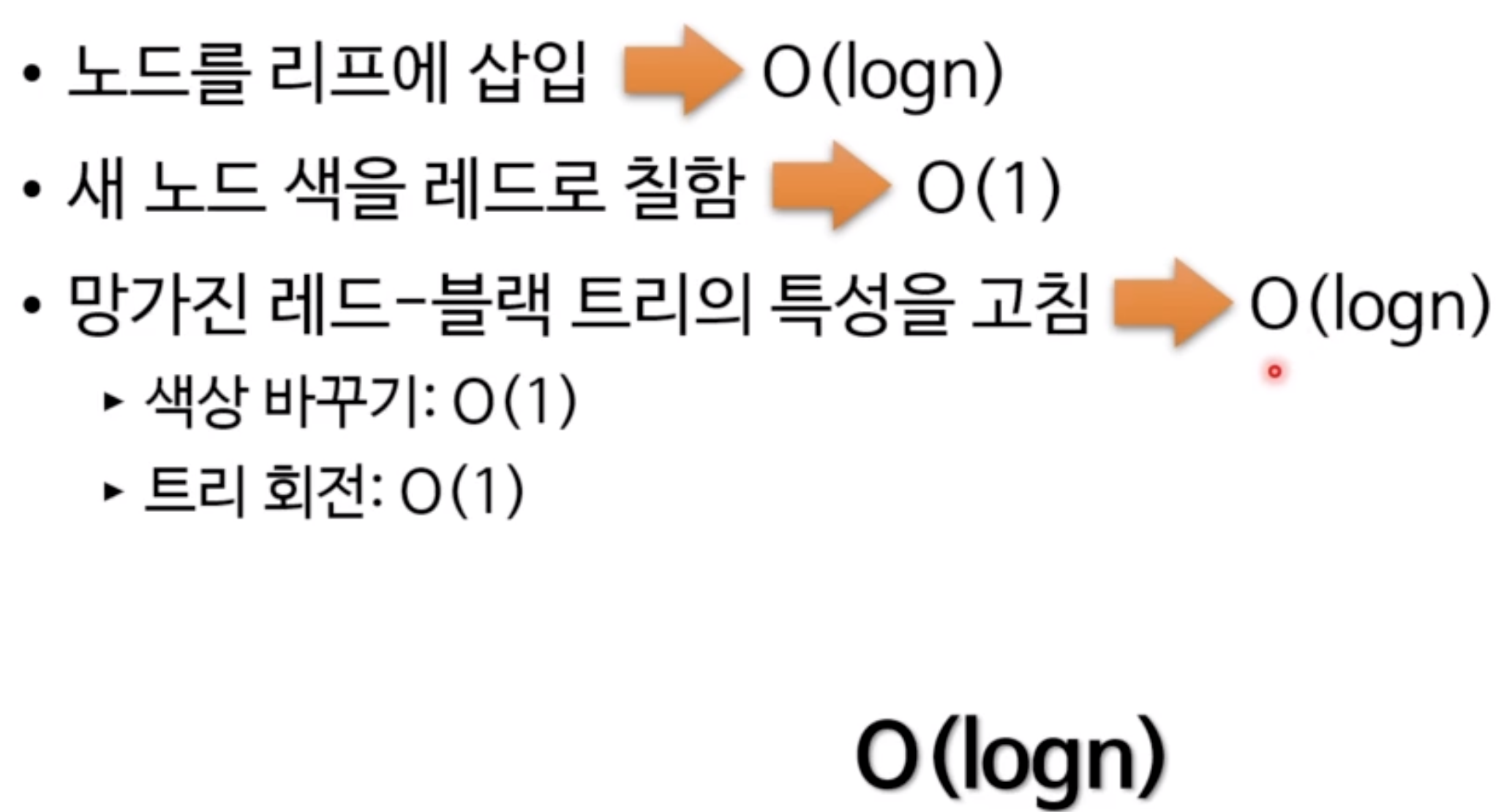
  • 모두 O(logN)
    • 삽입 혹은 삭제 : O(logN)
    • 트리 회전: O(1)
    • 색바꾸기: O(1)

레드-블랙 트리의 삽입/삭제 원리

• 삽입/삭제 원리를 스스로 알아내는 건 아마 천재의 영역...
  • 사실 완전히 이해하는 것 조차 쉽지 않음.
• 하지만 실무자라면 최소한 감은 잡아야 함.
  • 감을 익힌다면 아래와 같은 일이 가능한데,
    1. 데이터를 보고 레드-블랙 트리를 적용해야하는 상황을 인지
    2. 실제 코드를 구현하고 적절한 데이터로 테스트
    3. 추가 리서치

레드-블랙 트리의 삽입 방법(큰 그림)

1. BST와 똑같이 삽입

• 단, 새로 삽입하는 노드는 언제나 레드
• 언제나 리프에 추가되니(BST에서 삽입은 무조건 리프에 했었음.) 아래 연산이 간단해짐

2. 레드-블랙 트리의 조건을 만족하도록 재귀적으로 고침

• 재귀 방향: 리프로부터 위로 올라가면서
• 고칠때 사용하는 기법은 두가지
  1. 트리 회전(tree rotation)
  2. 색깔 바꾸기
• 총 4가지 상황(패턴)에 따라 트리 회전, 색깔바꾸기 기법을 다르게 적용.

즐거운(?) 삽입문제

case 1: N이 루트

case 2: P(부모)가 블랙인 경우

• 부모가 블랙인 경우 case 1(레드-블랙트리 규칙이 깨짐)
  
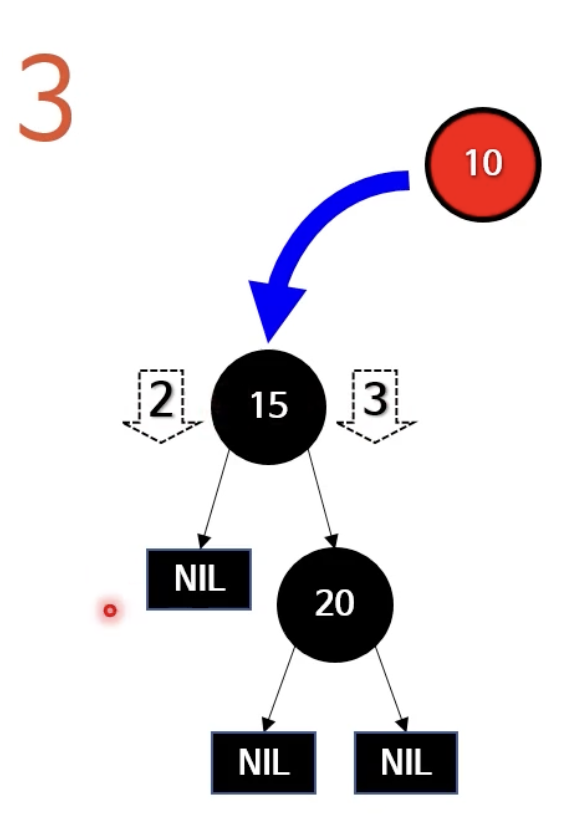
• 부모가 블랙인 경우 case2(레드-블랙 규칙 만족)
  
  

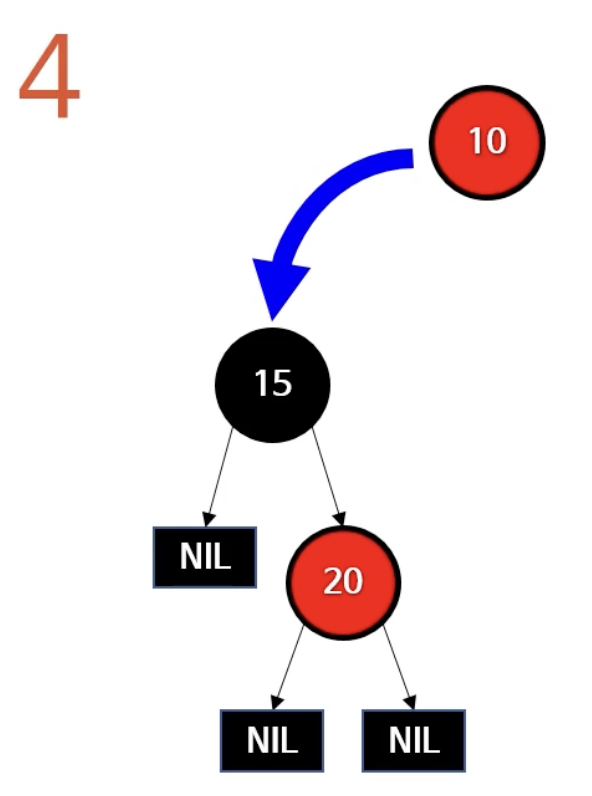
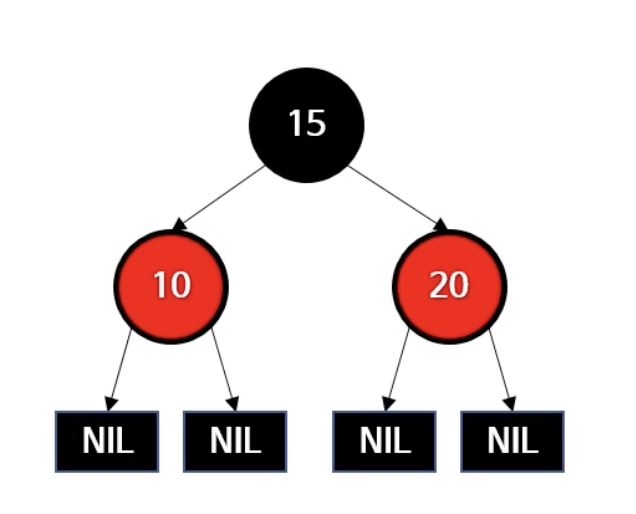
case 3: U(삼촌)가 레드

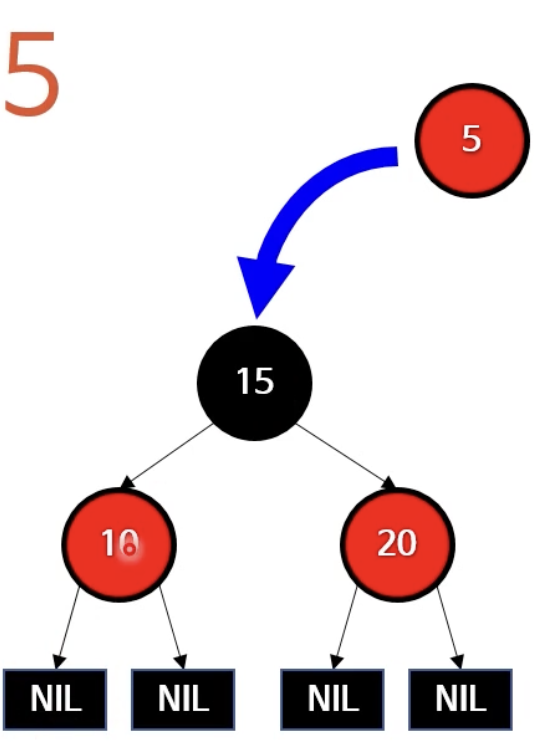
• 이걸 해결해야함.
  
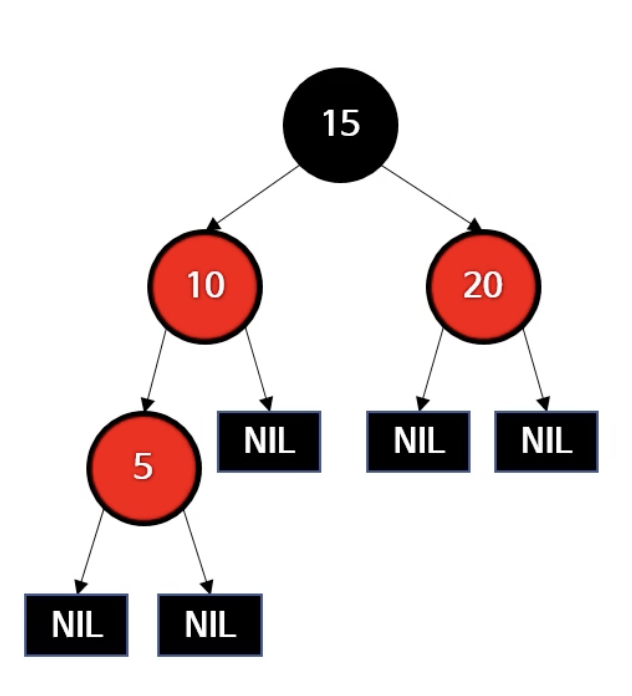
• 위 경우를 해결하는 방법은?
  1. 5를 Black으로 바꿈
     • 블랙 높이가 일정하지 않아짐
  2. 10을 Black으로 바꿈
     • 블랙 높이가 일정하지 않아짐
  3. 10과 20을 Black으로 바꿈
     • 트리 조건을 모두 만족함. 그러나...
• 끝인줄 알았지만.. 이런 경우도 있을 수 있다!
  
  
  
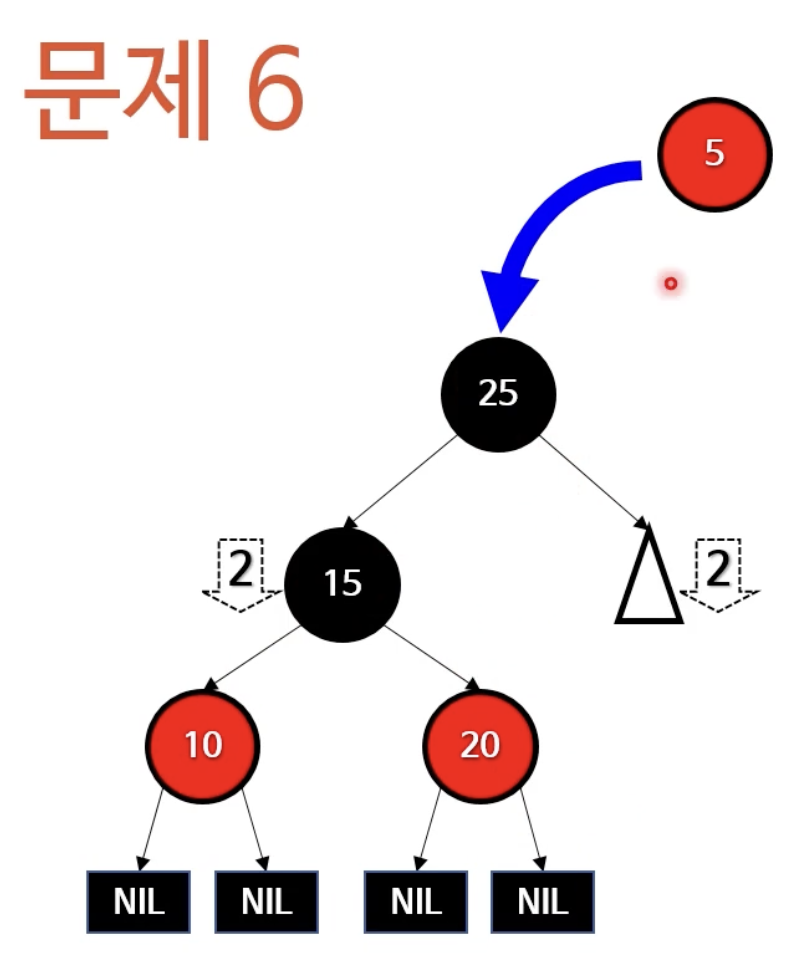
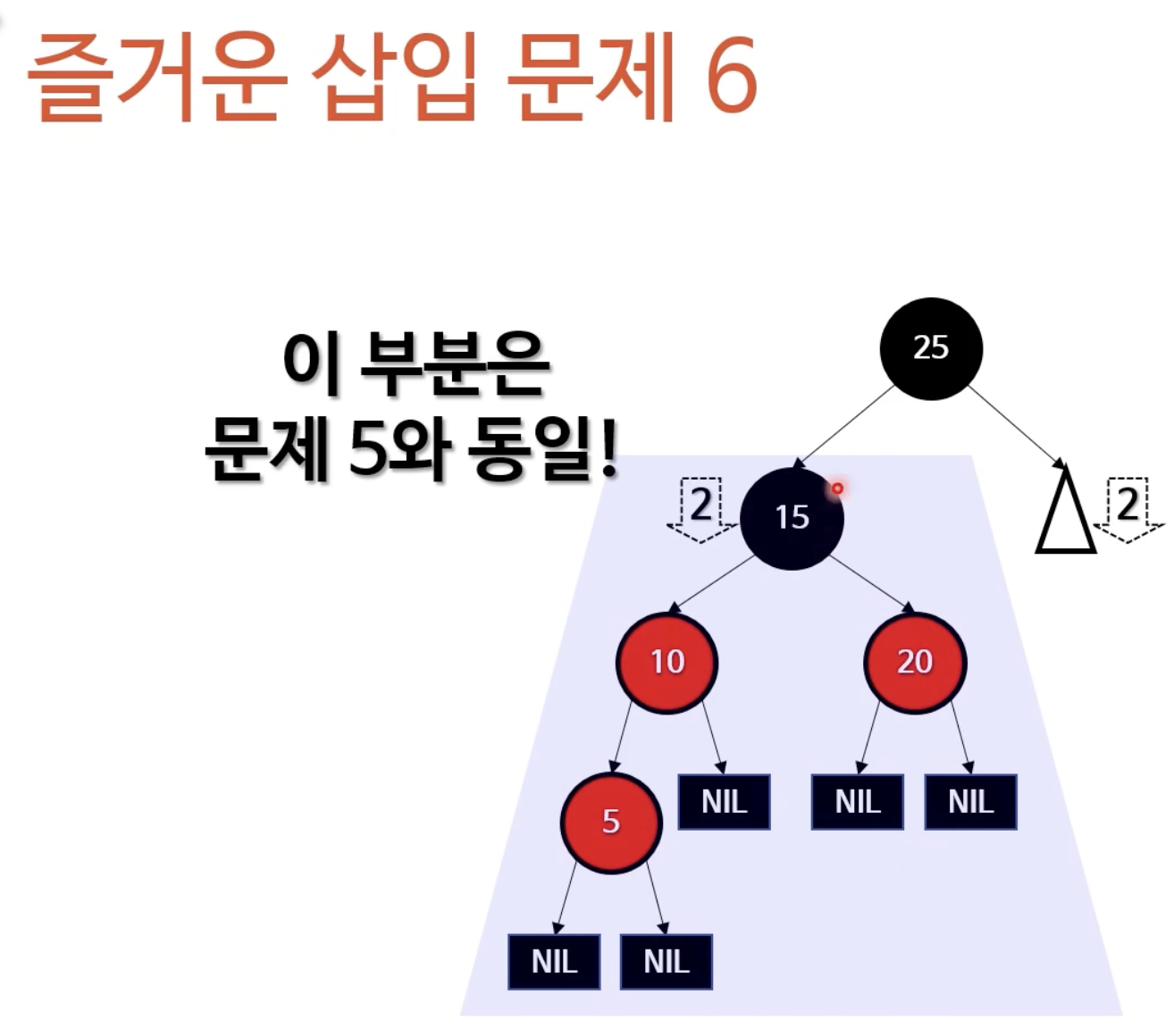
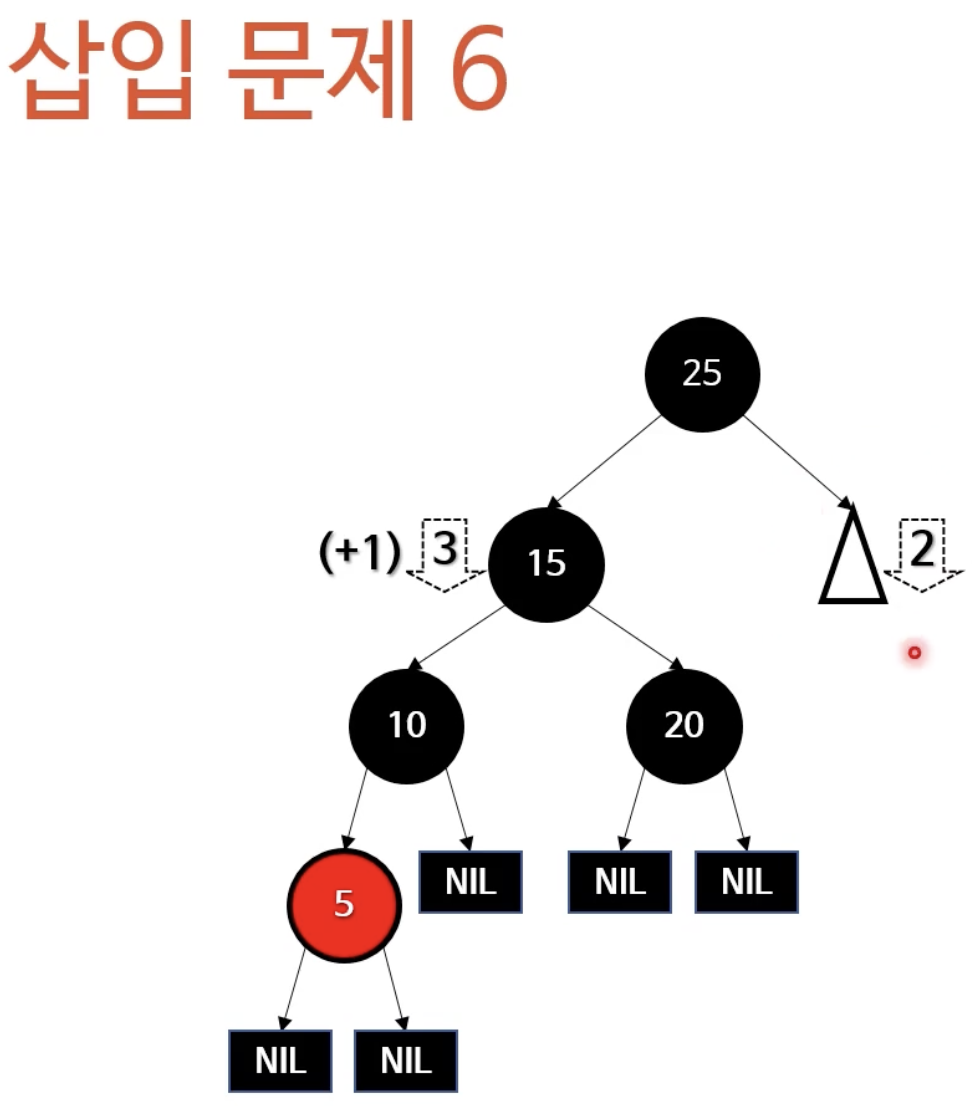
• 맨 처음 봤던 노드의 경우 NIL을 제외한 자식노드가 왼쪽, 오른쪽 각각1개일때의 경우였다. 그 다음경우는 루트노드를 기준으로 자식노드가 또다른 자식을 갖는 경우이다. 이 경우 우리가 앞에서 했던 부모와 삼촌 노드의 색을 바꾸는것만으로는 문제가 해결되지 않는다. 그래서 이경우는 아래 그림과 같이 조부모의 색을 바꿔주어 해결할 수 있다.
  
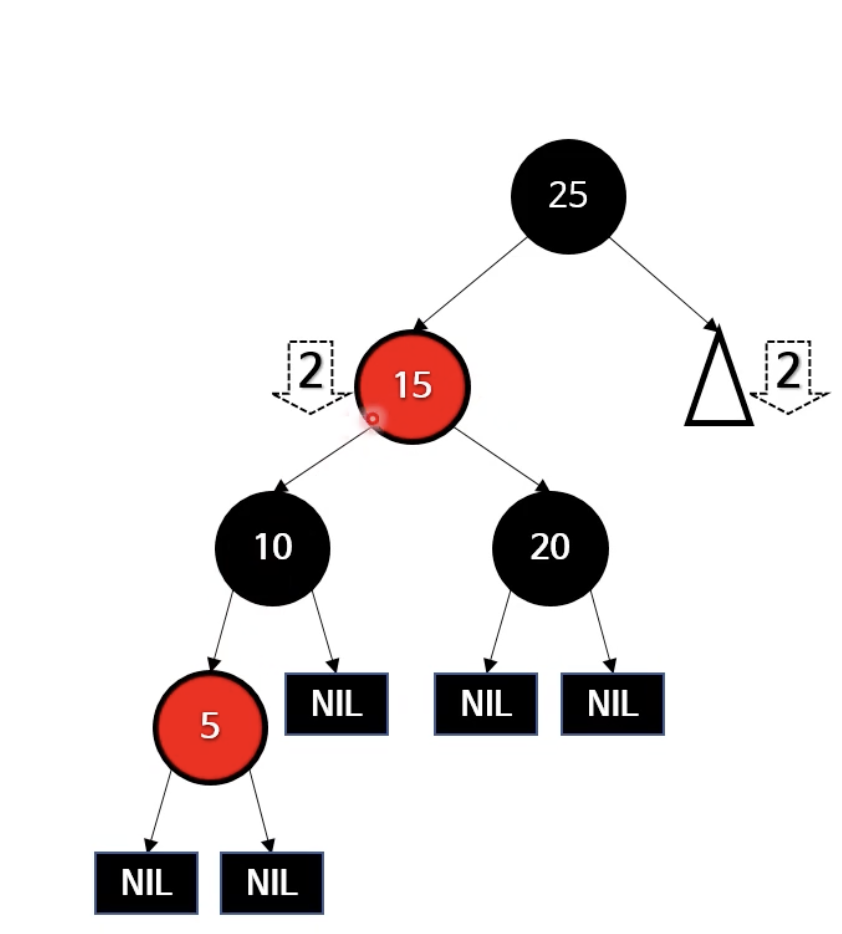
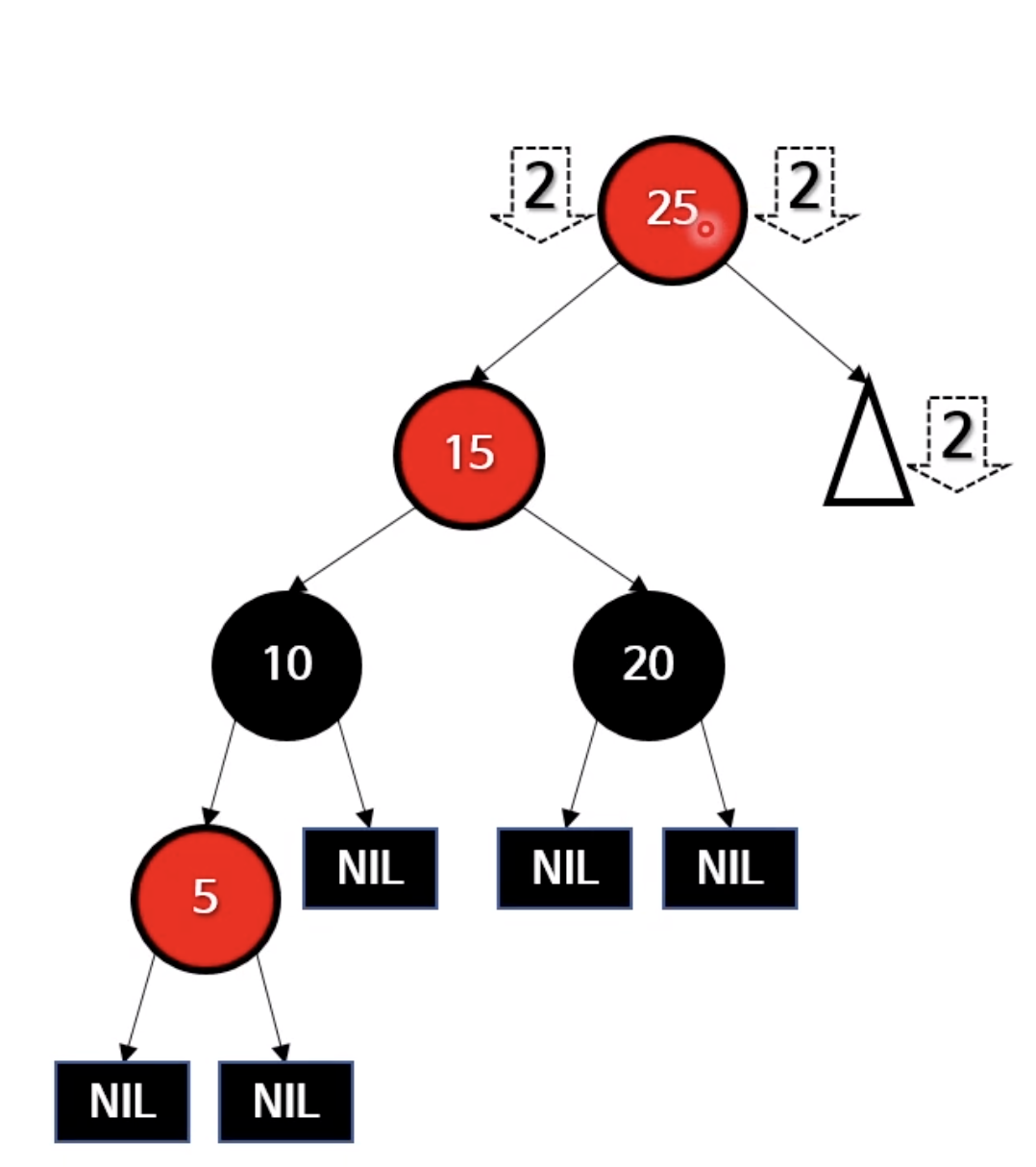
• 그런데 아래 문제도 위에 찾은 방법으로 풀 수 있다.
  
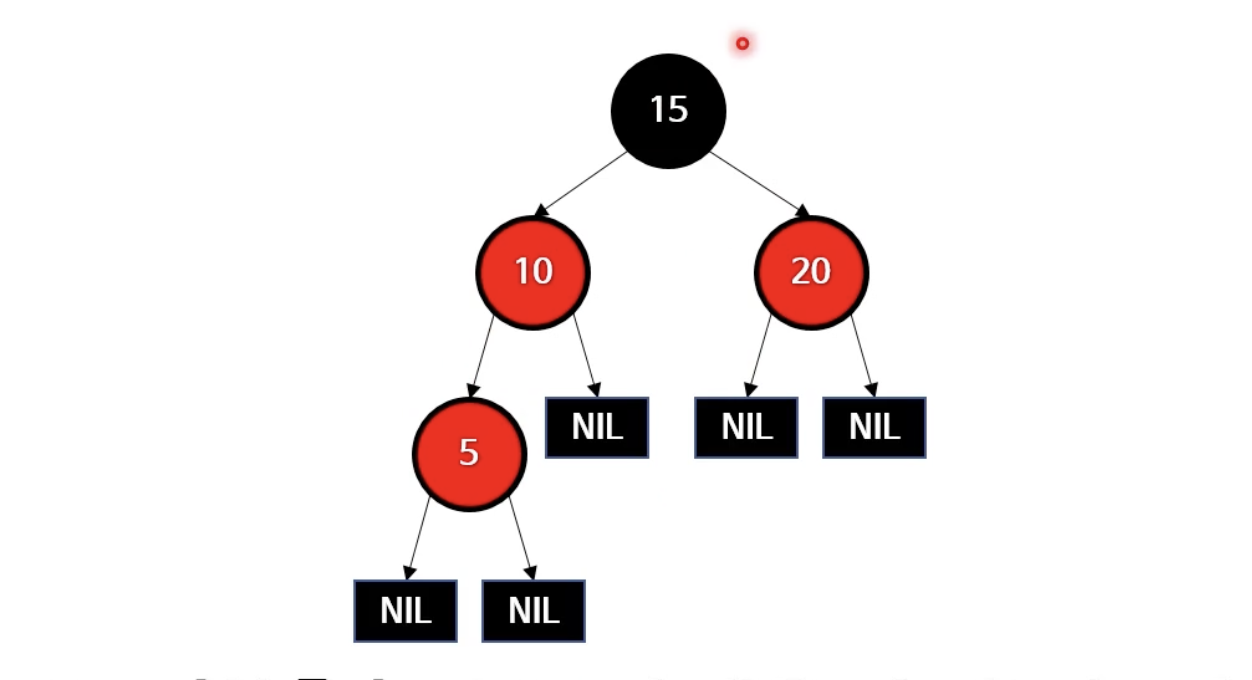
  1. 5의 부모와 삼촌을 블랙으로 바꾸고 조부모를 레드로 바꾼다.
  2. 조부모가 루트노드이므로 조부모의 색을 블랙으로 바꿔준다(Case 1을 적용)

case 4: U(삼촌)가 블랙

• 이 부분은 앞과 다르게 주먹구구식으로라도 접근하기가 어려운 케이스임. 문제는 아래와 같음.
  
• 위 그림은 6번문제의 해법에서 가져왔다. 만약 root가 레드인 경우에 어떻게 풀수 있을까?
• 이런 상황에서 사용하는것이 바로 트리 회전이다. 트리를 회전한 그림은 아래와 같다.
  
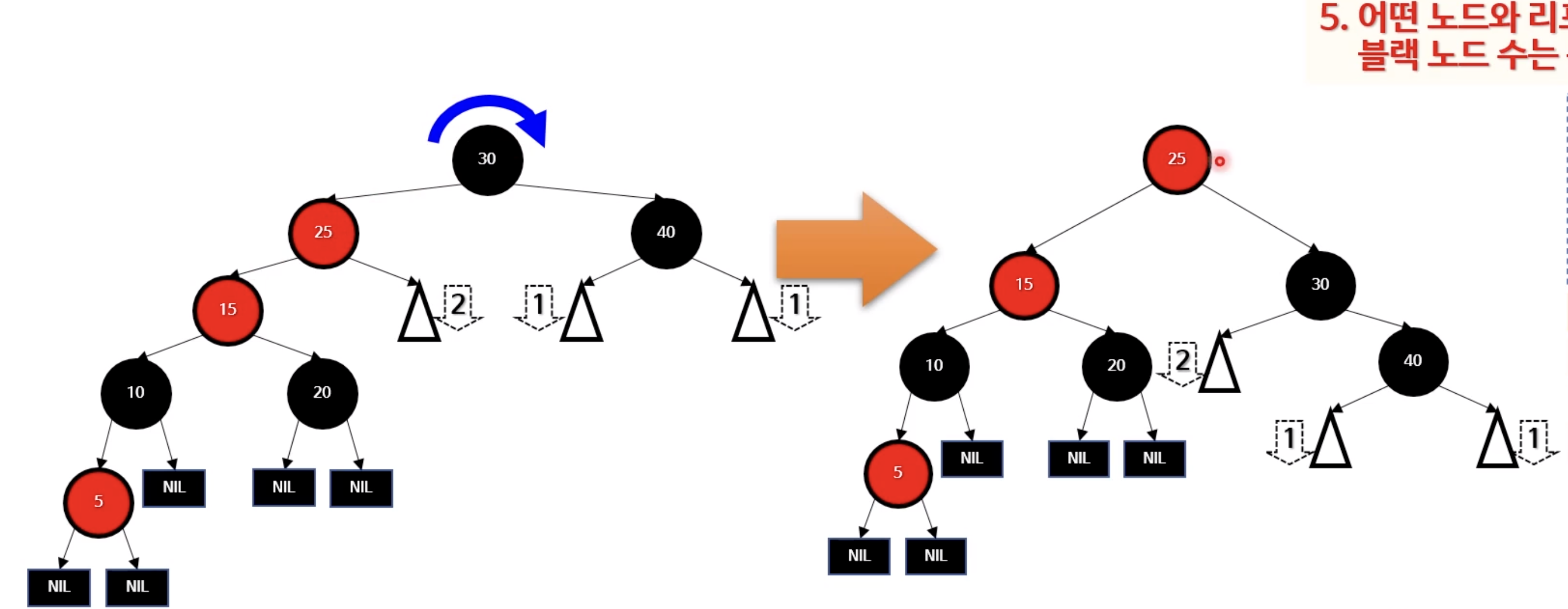
• 트리를 회전하는것을 말로 정리해보면
  1. 루트노드가 오른쪽으로 밀려나고
  2. 루트노드는 루트노드의 left였던 25가 된다.
  3. 이 과정에서 30의 right에는 25의 right가 들어가게된다.

트리회전 결과

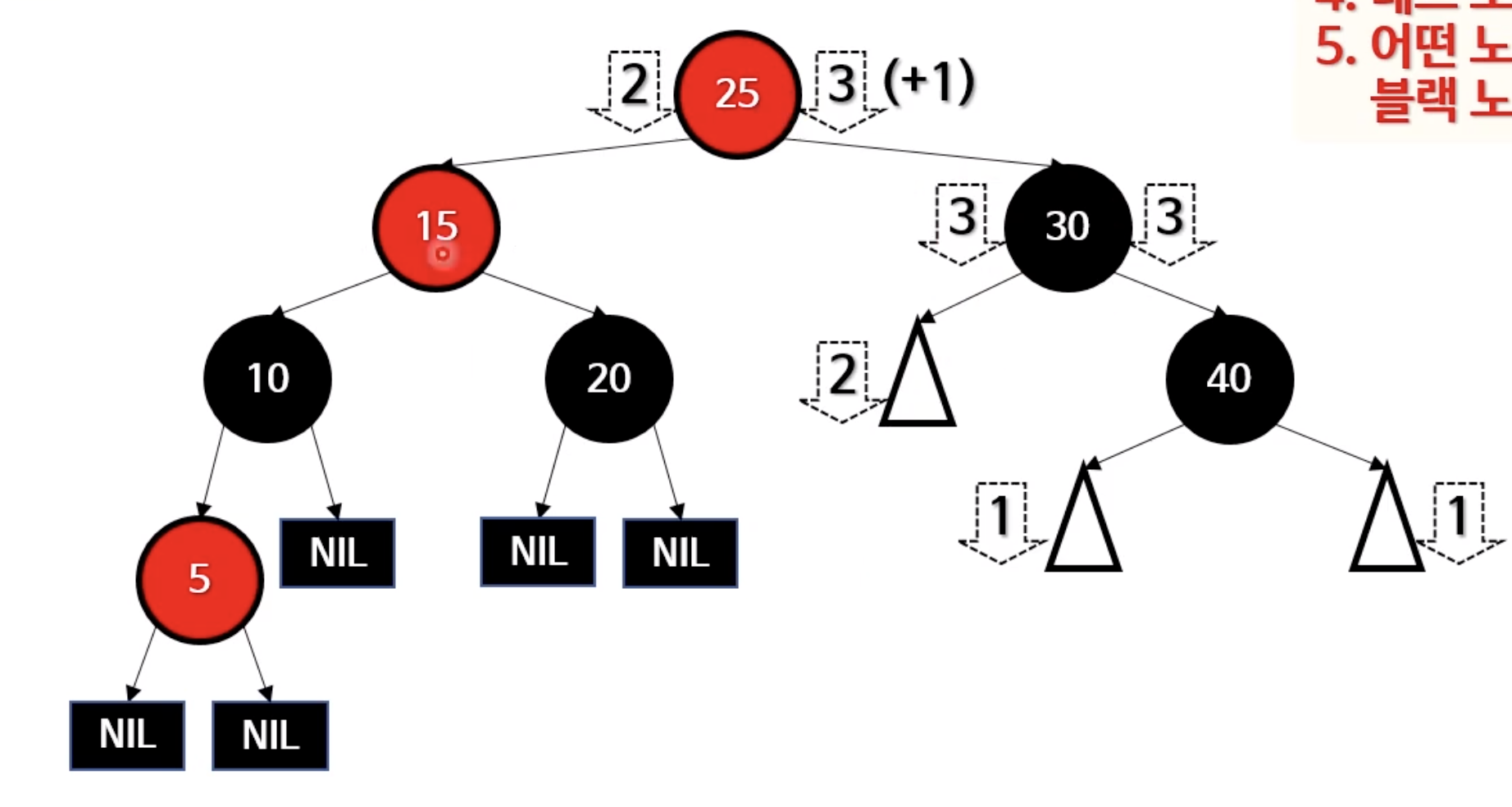
• 이해할 수 있는 영역이 아닌것같지만.. 위 상황에서 트리의 균형을 맞춰주기위한 해결책은 30의 색을 레드로 바꿔주면 된다. 그것이 아래의 결과이다.
  

산넘어 산

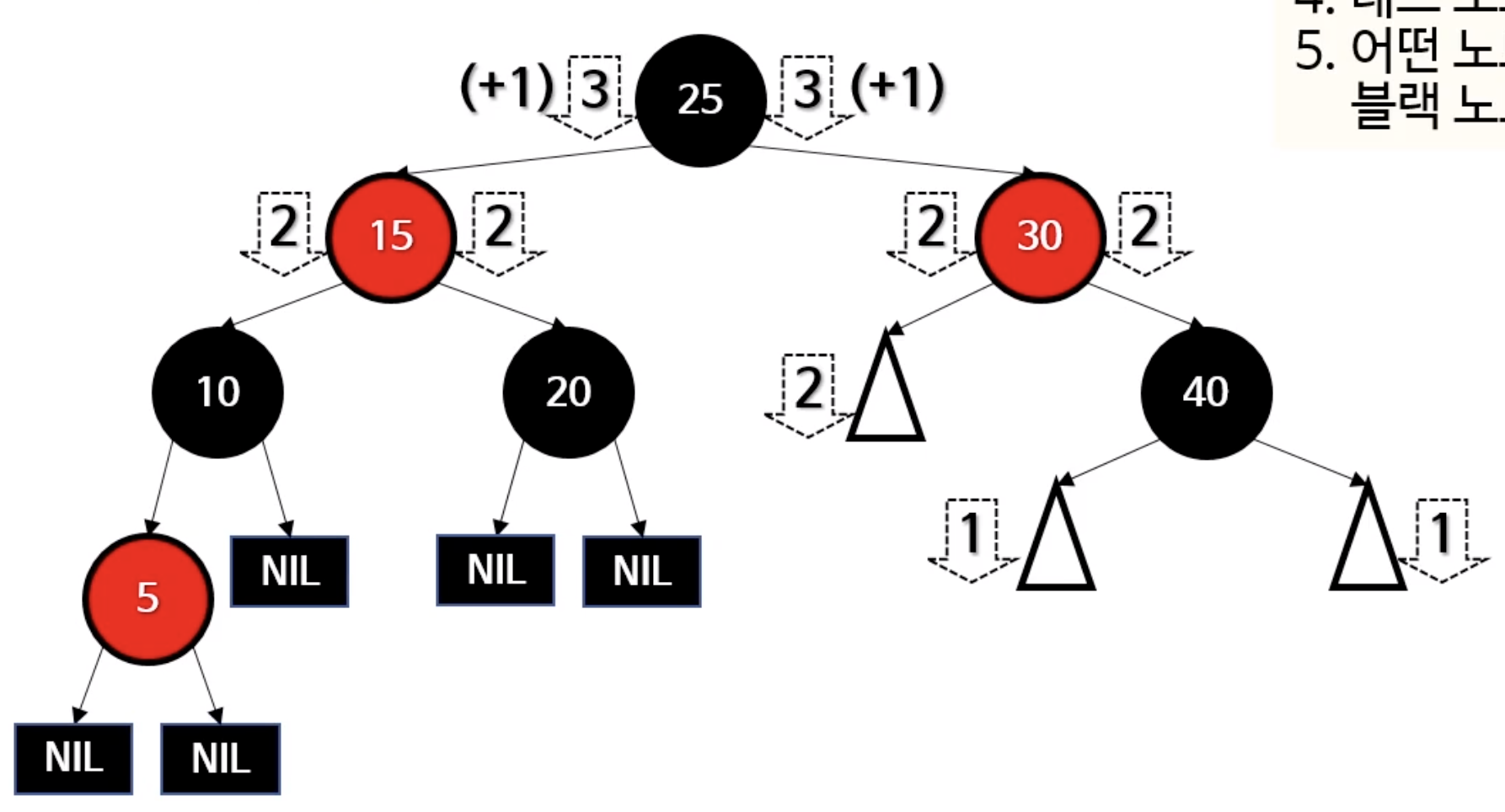
위의 문제를 방금전 case4와 같이 풀어보려고 시도한다면..?

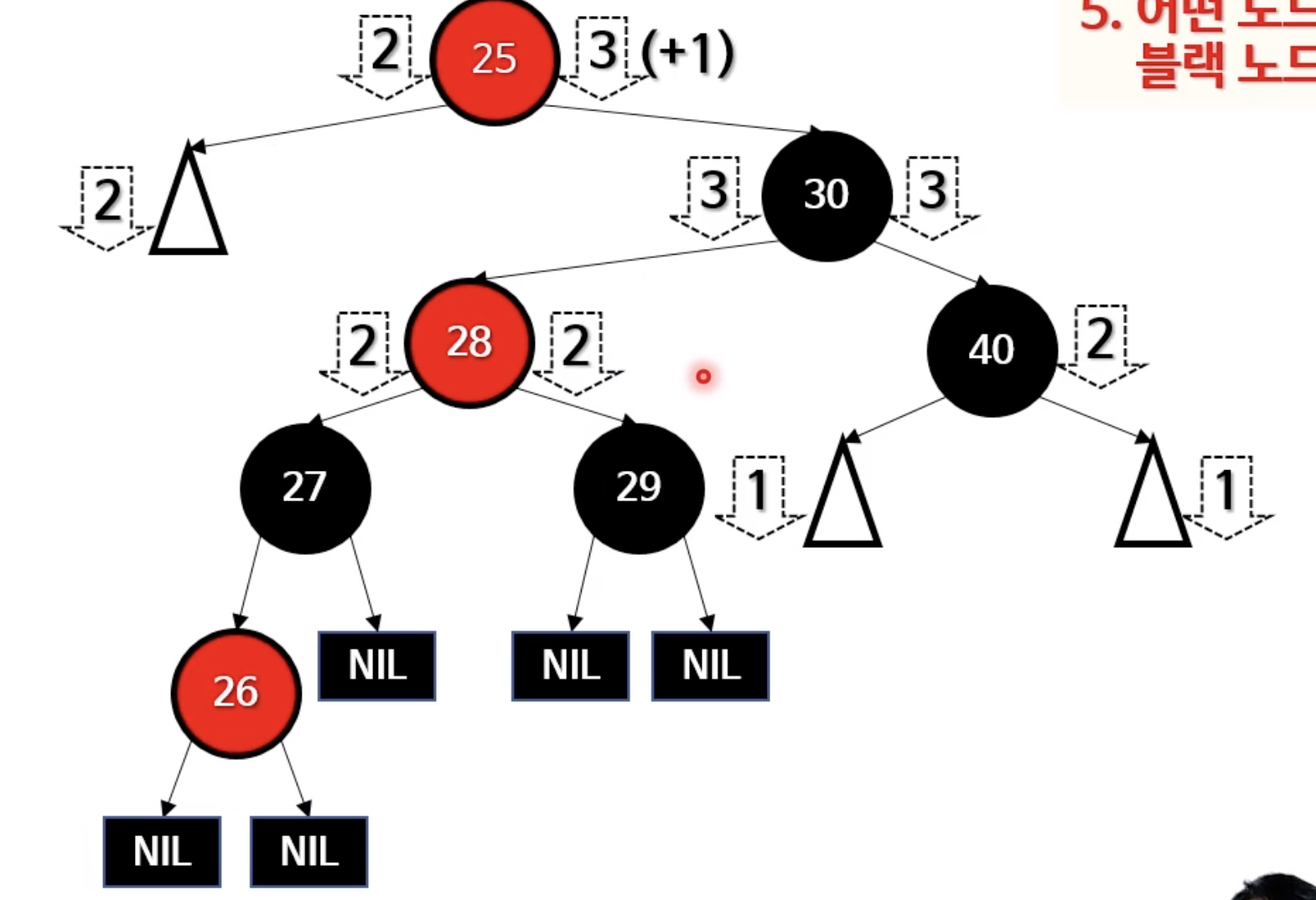
한쪽으로 쏠려버린 모습을 보게된다. 그렇다면 어떻게 접근해야할까?

• 레드-블랙트리 전략설명할때 트리가 일직선인지 아니면 꺾여있는지를 파악한다고 한다.
  아래 그림과같이 말이다.
  
  

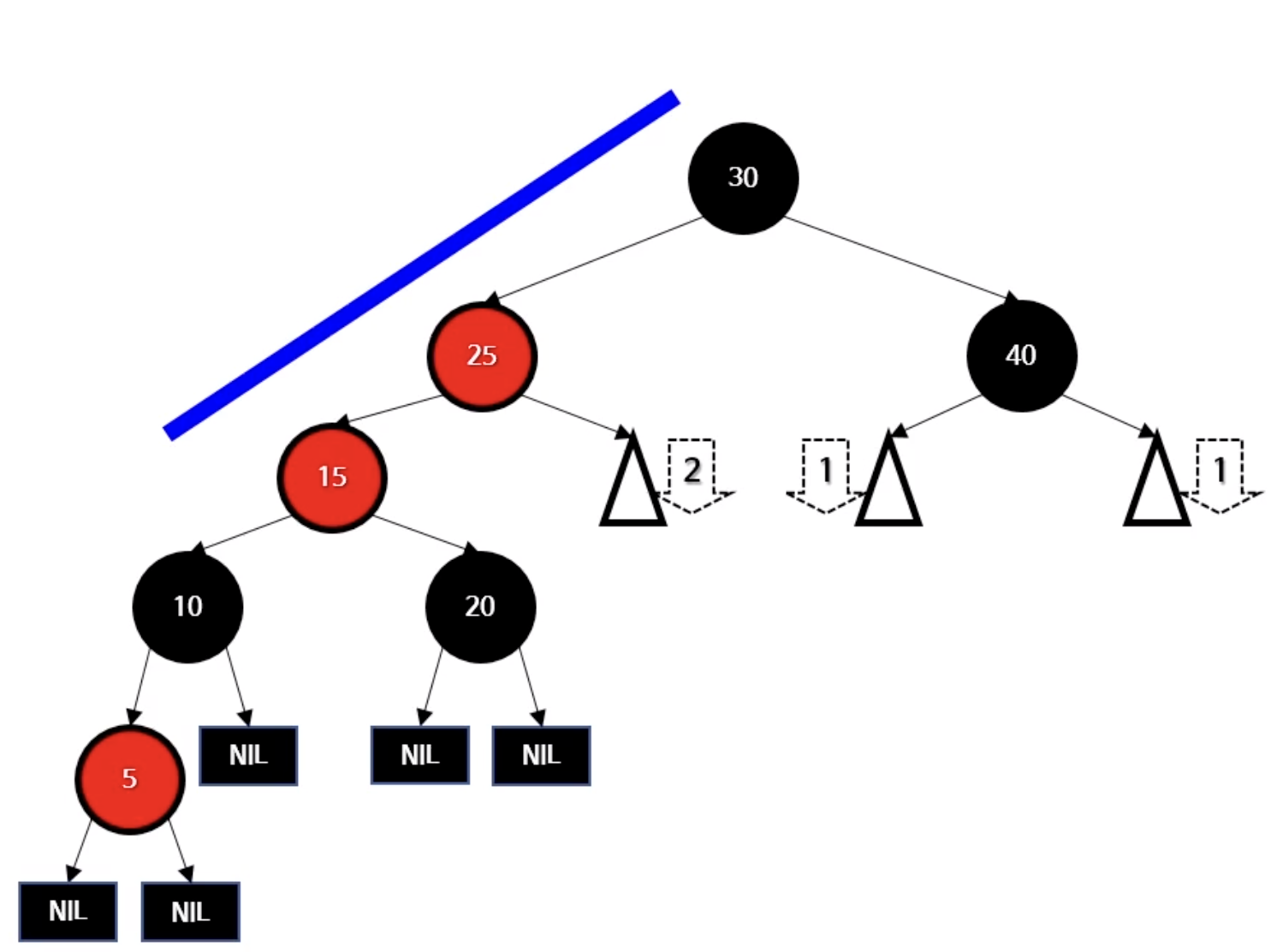
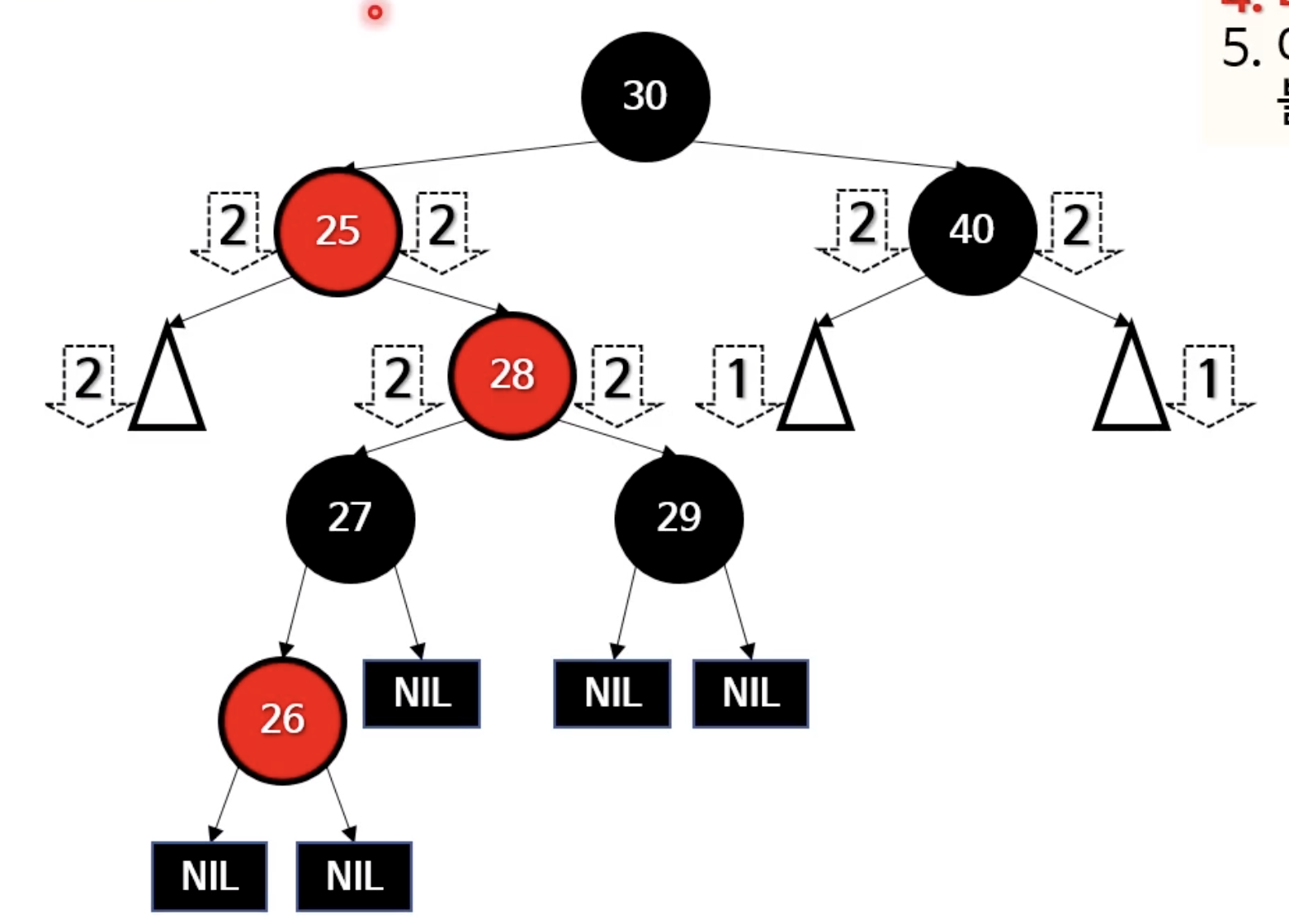
이번에는 트리의 회전을 루트에서 하는것이 아닌 25를 기준으로 왼쪽으로하면 어떨까? 그러면 그 하위트리들이 회전되면서 뭔가 정렬이 잘 이뤄지지 않을까?

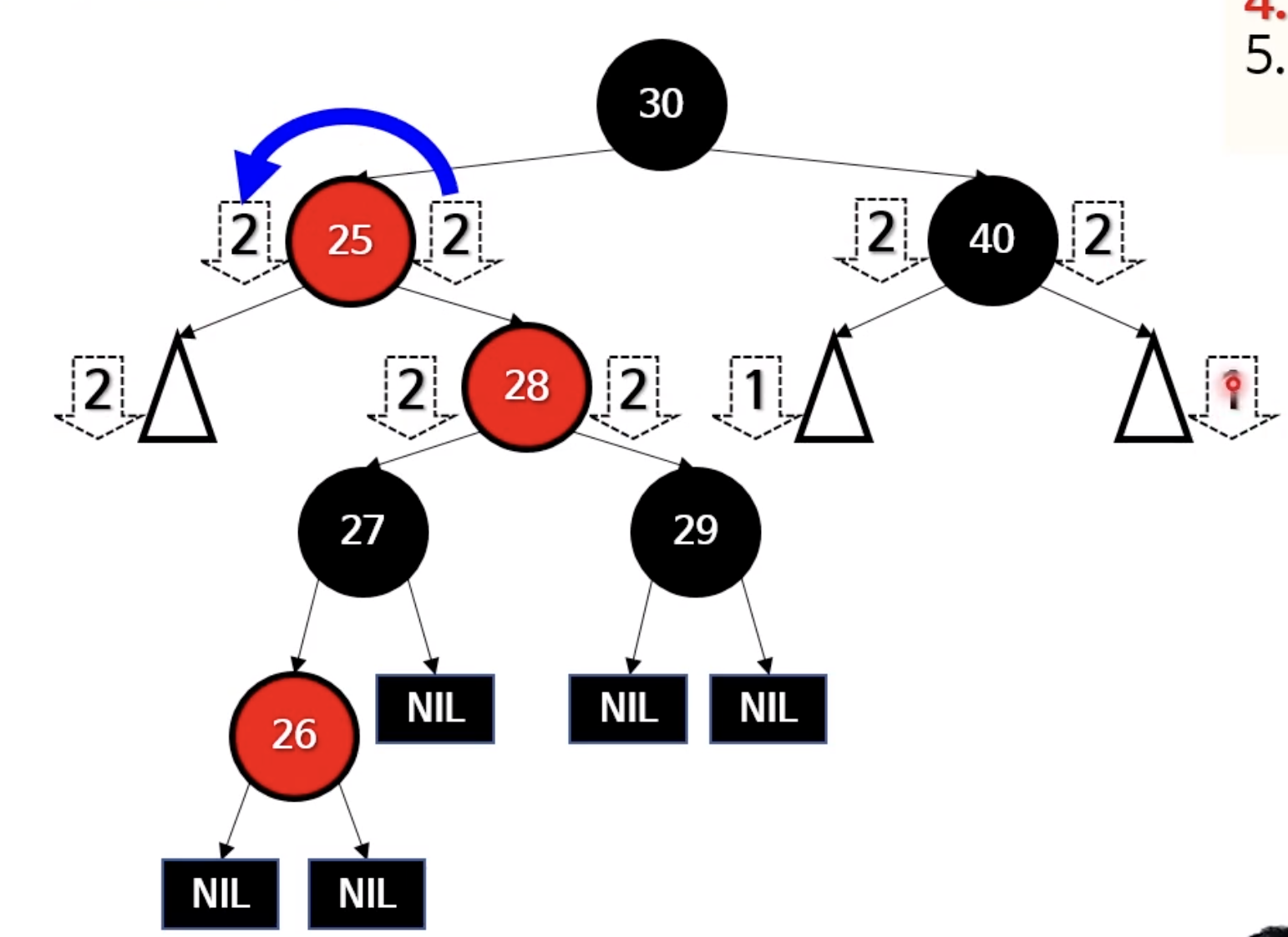
1. 25가 왼쪽으로 내려오고
2. 28이 루트노드가 된다.
3. 28.left = 25
4. 28.right = 29
5. 27이 25의 right로 들어간다.

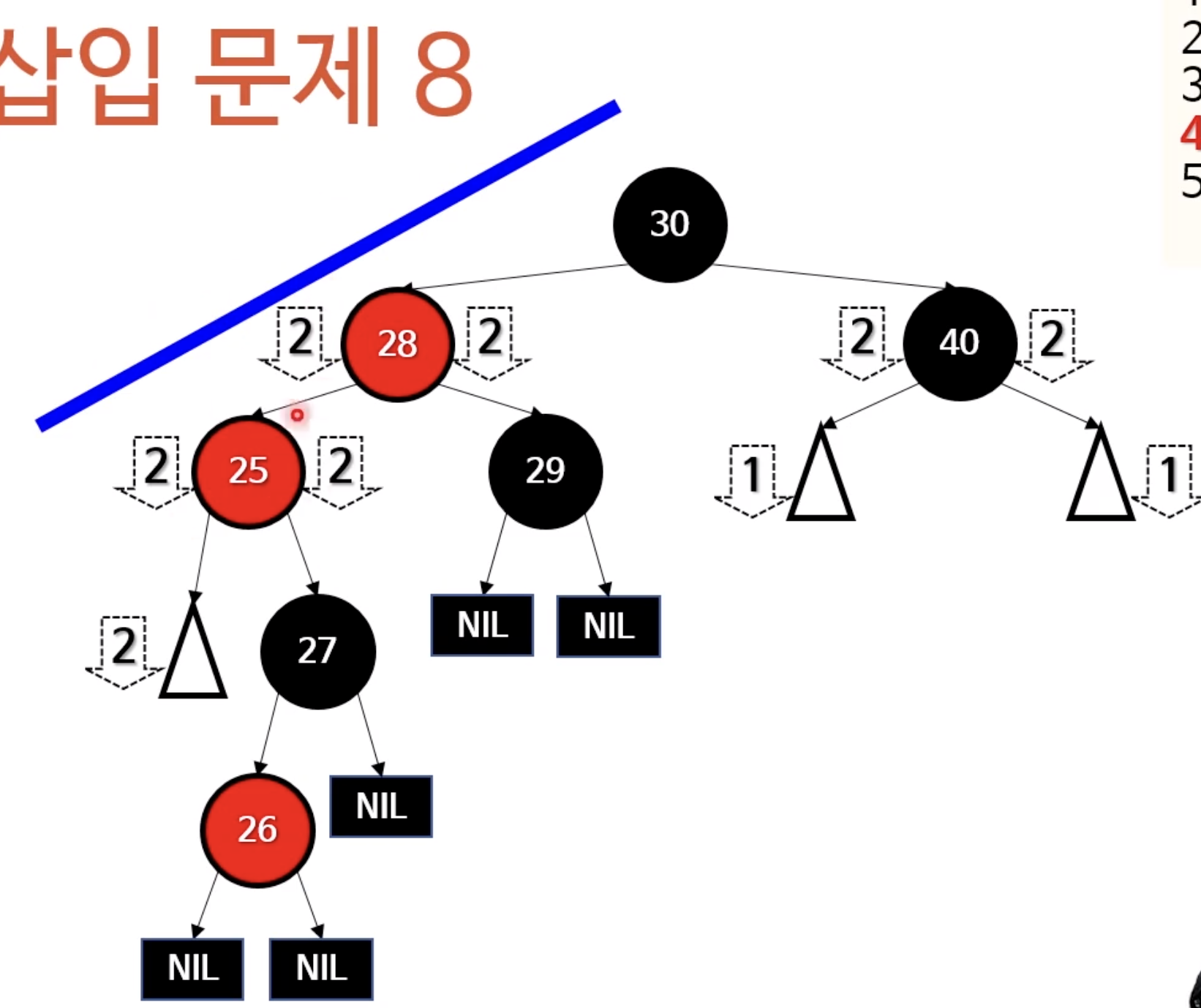
위와같이 하면 이쁘게(?) 정렬된다. 이것을 루트노드기준으로 오른쪽 회전하면?

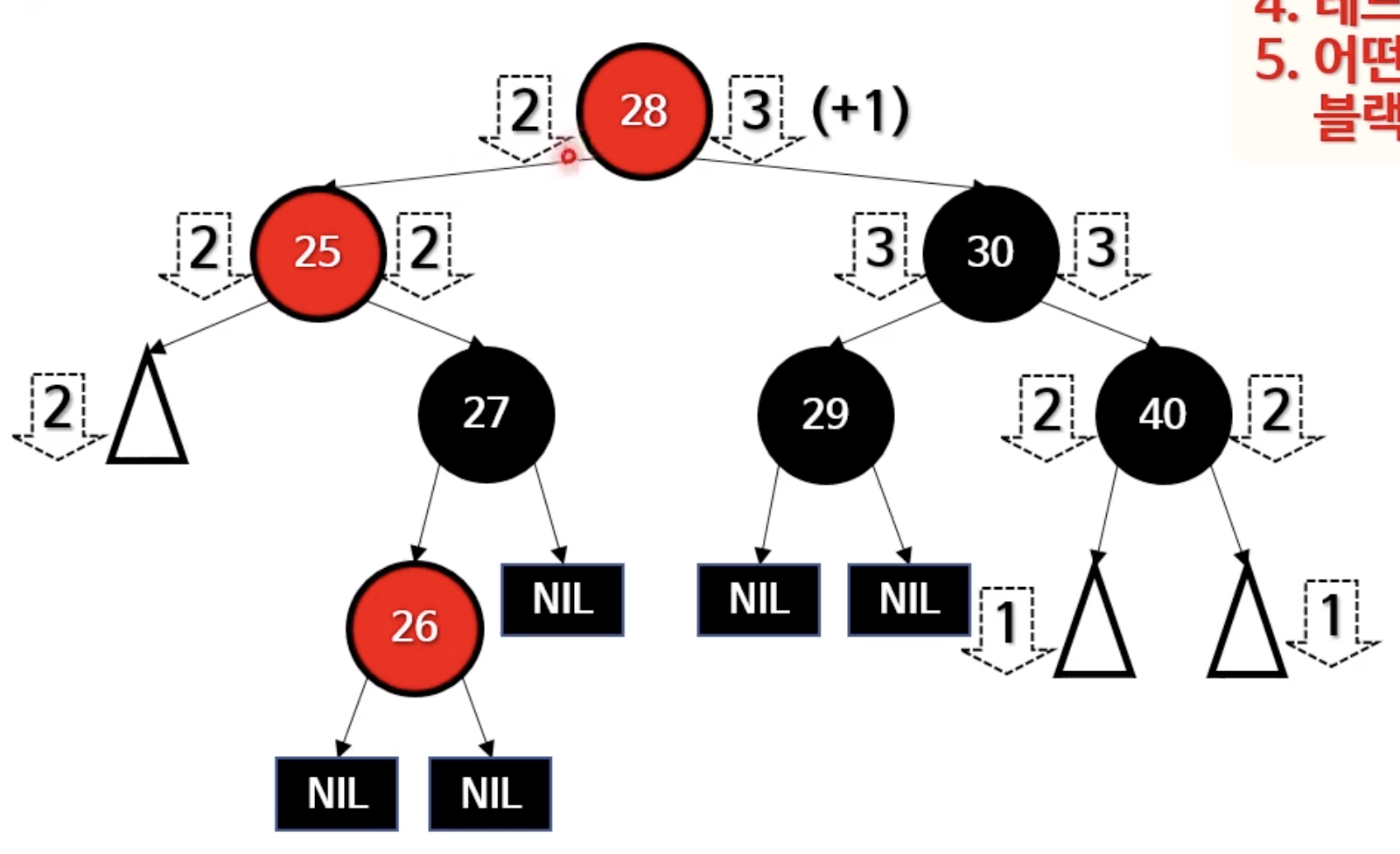
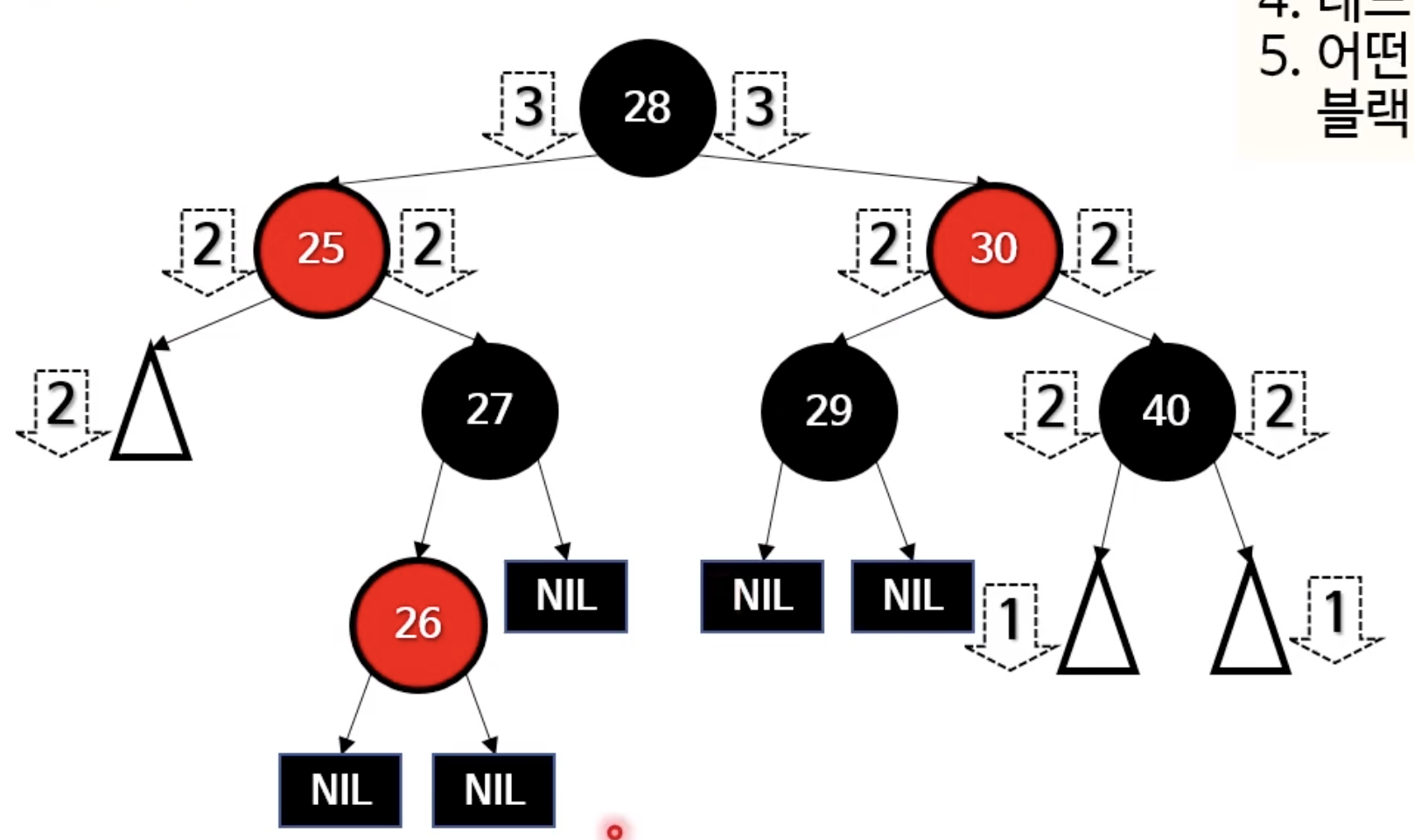
여기서 28 과 30의 색을 바꿔주면 완성!

시간복잡도

앞에서 본 예시는 노드가 왼쪽에 추가되는 경우만 보았다. 그렇다면 만약 새 노드가 오른쪽에 추가된다면?

• 사실 오른쪽에 추가되어도 해법은 똑같다.
• 4가지 상황(case)를 잘 정리한게 전략(strategy)이다.
• 보통 필요할때마다 찾아보며 해결한다고 함.

정리

case 1

• 상황: 현재 노드 N이 트리의 루트
• 전략: N을 블랙으로 바꾼다.
  

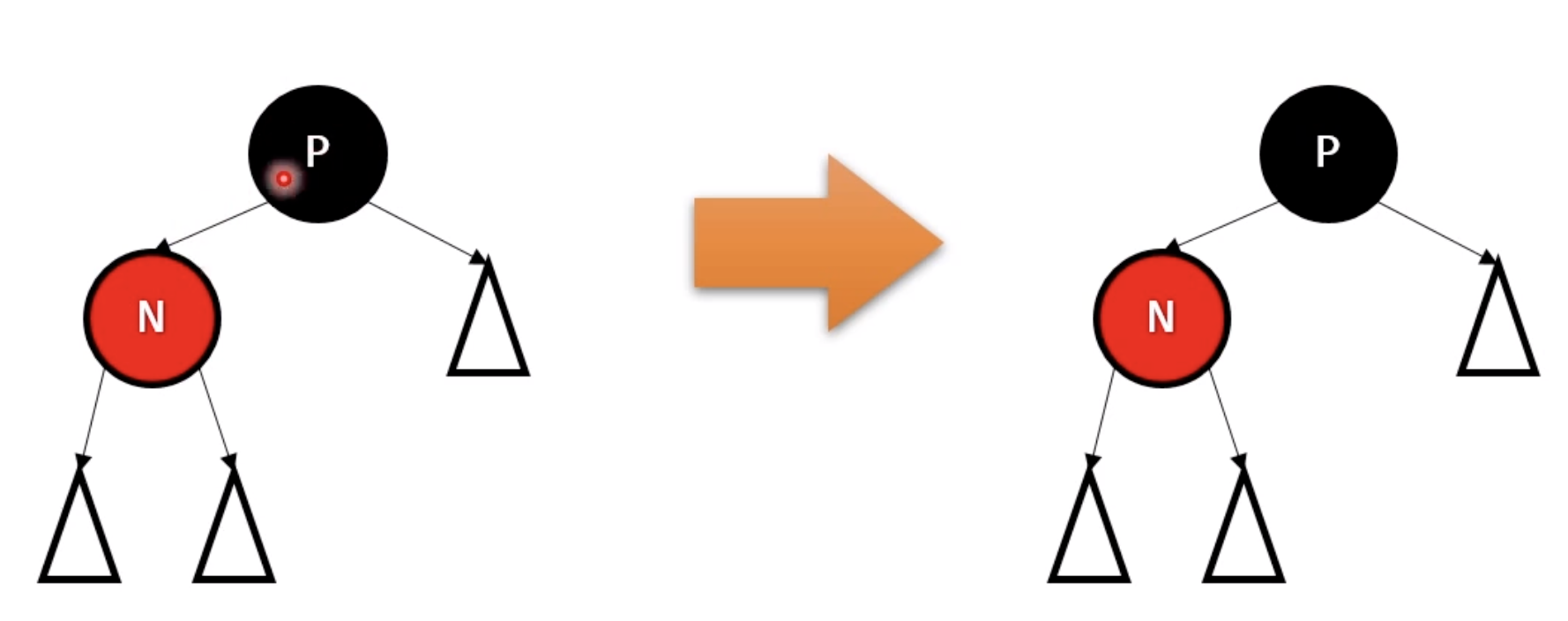
case 2

• 상황: N의 부모 P가 블랙
• 전략: 아무것도 하지않음.
  

case 3

• 상황: P와 삼촌 U가 모두 레드, 조부모 G는 블랙
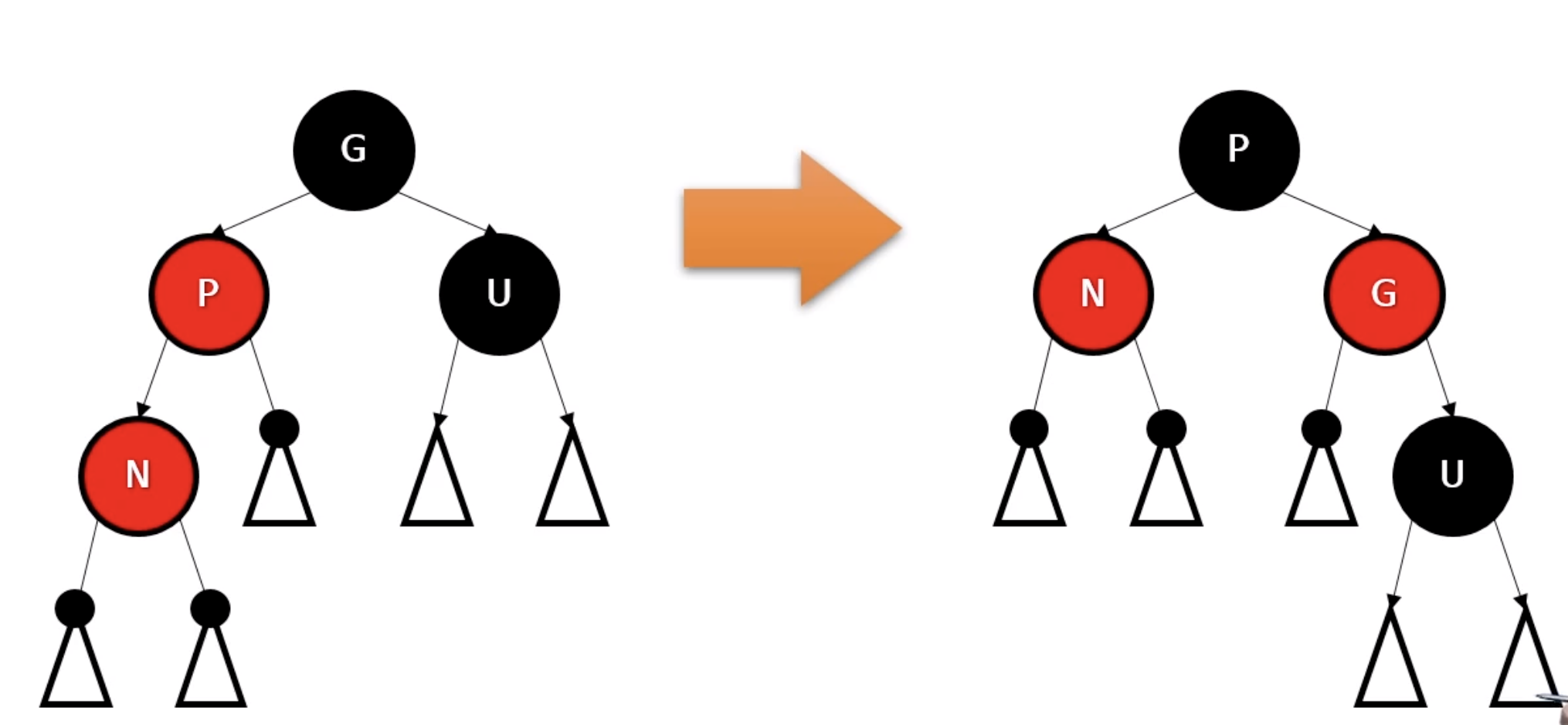
• 전략: P, U, G의 색을 바꾼다. 그 후 G를 N으로 놓고 case 3을 다시 실행한다. 만약 N 이 루트노드이면 case1을 적용한다.
  

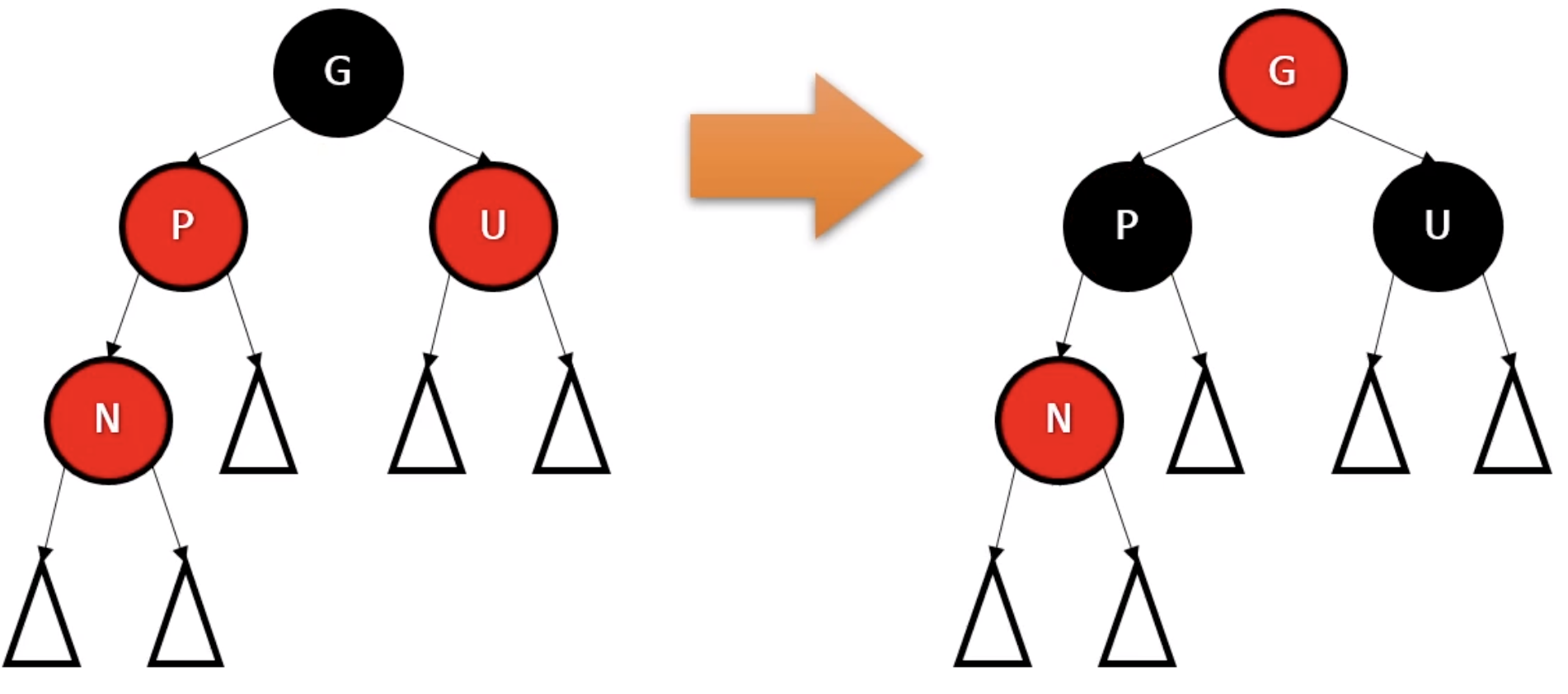
case 4

• 상황: P는 레드, U는 블랙
• 전략: N이 하위 트리의 안쪽에 있지 않도록 회전. 그 후 2단계로 진행.

단계1

• 단계 1 그림에서 삼각형 노드 위에 검정색 동그라미의 의미는 다른 노드보다 블랙높이가 +1 이라는것을 표시한것임.
  

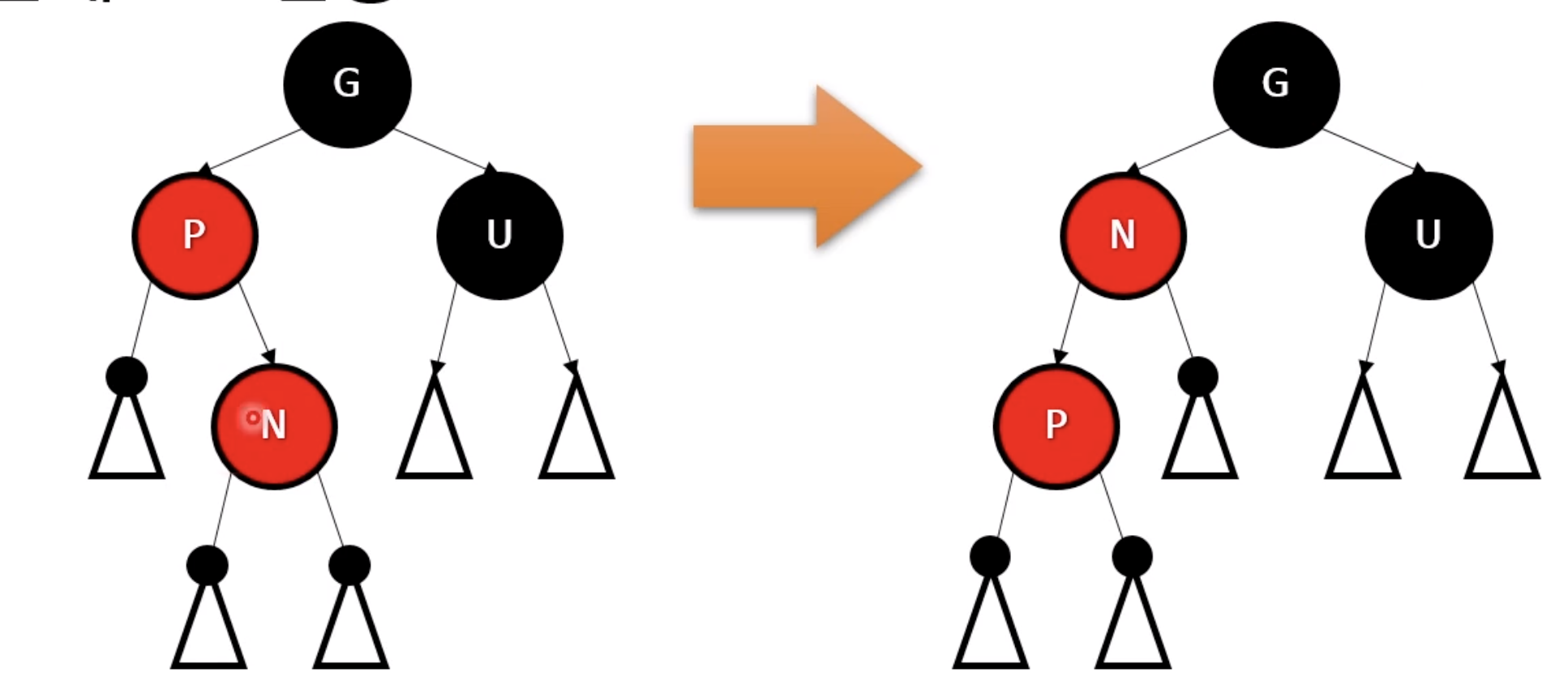
단계2

• 상황: 이제 N이 하위 트리의 바깥쪽에 있음
• 전략: G에서 우회전 후 P와G의 색을 바꿈