레드-블랙 트리

Intro

• 각 노드가 레드 혹은 블랙
  • 노드에 저장하는 데이터가 아님
  • 그냥 1비트짜리 추가 정보(굳이 빨강/검정이 아니어도 되지만, 일반적으로 레드/블랙을 사용한다고 함)
• 스스로 균형을 잡는(self-balancing)트리
  • 트리 높이를 최소로 보장
  • 균형을 잡는 시점은 삽입/삭제시
  • 그외 연산은 BST와 동일(단, 탐색속도가 BST보다 빠름)
  • 레드와 블랙사이의 균형을 잡는다고 함.(이게 뭔소리지?)

레드-블랙트리의 특성

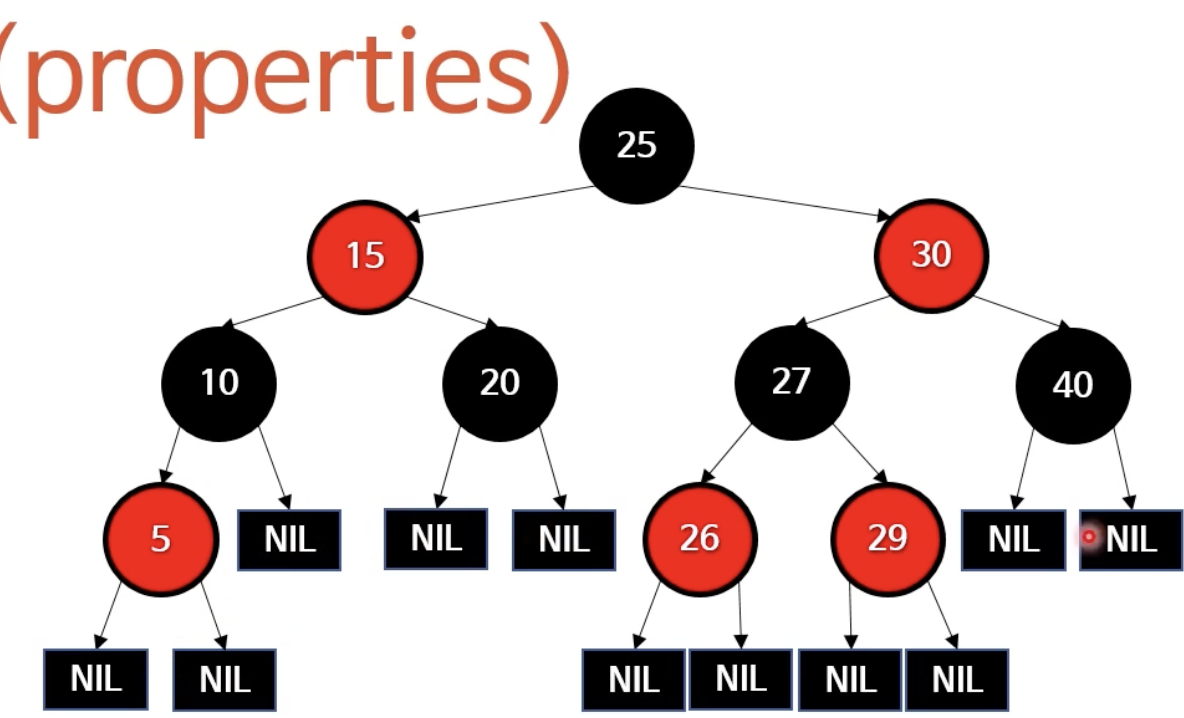
1. 노드는 레드 or 블랙이다.
2. 루트노드는 언제나 블랙이다.
3. 모든 리프노드(null 포인터)는 블랙이다.
4. 레드 노드의 자식은 모두 블랙이다.
5. 어떤 노드와 리프 사이에 있는(=블랙 높이) 블랙노드 수는 동일하다.

• 블랙노드에만 있는 제약
• 이를 통해 블랙과 레드 노드 수의 균형을 맞춤
• 이걸위해 삽입/삭제시 트리를 재배치하거나 노드의 색을 바꾸기도 함.

레드-블랙트리 특성의 영향

• 리프노드는 데이터를 담지 않음(=null)
• 다음과 같은 용어가 탄생함.
  • 블랙 깊이(black depth): 루트와 어떤 노드사이에 있는 블랙노드 수
  • 블랙 높이(black height): 어떤 노드와 리프 사이에 있는 블랙 수
• 가장 큰 리프 깊이가 가장 작은것의 2배를 넘지 않음(=트리가 한쪽으로 쏠리지 않는다.)
  • 레드-블랙트리가 보장하는 핵심 특성!
  • 이진 트리 연산시간이 O(N)이 되는 최악의 경우를 방지 == O(logN)을 보장
  • C++의 std::map의 구현으로 일반적으로 사용되는 자료구조!

레드-블랙 트리가 보장하는 핵심특성의 증명

• 블랙 높이가 x인 트리가 있다고 해보자.
• 루트 -> 리프의 길이가 최소인 경우는?
  • 블랙: x개
  • 레드: 0개
  • 왜냐하면 블랙노드 아래에는 레드 or 블랙노드 모두 올 수 있지만 레드노드 밑에는 레드노드가 올 수 없기때문에 블랙노드만 들어갈 수 있다. 따라서 최소길이가 나오는 경우는 블랙노드만 있을때 뿐이다.
• 이제 레드노드를 최대한 집어넣으려 시도하면?
  • 블랙 노드 사이에 하나씩만 넣을 수 있음.
• 따라서 루트 -> 리프의 최대높이는 2x개의 노드로 구성
  • 블랙: x개
  • 레드: x개
  • 참고: NIL 리프노드는 세지 않음.
• 위의 이유로 한쪽으로 쏠린다해도 반대쪽의 2배를 넘을 수 없다.

결론

• 레드-블랙 트리가 균형잡힌 트리인 이유는 트리가 한쪽으로 쏠려 최악의 상황인 LinkedList와 같은 모양이 될 수 없도록 설계되었기 때문이다.
• 레드-블랙 트리는 삽입, 삭제시 트리의 균형이 깨지지않게 잡아준다.