정렬 알고리듬

서정한·2023년 6월 8일

병합정렬 삽입정렬 선택정렬 알고리듬 정렬알고리듬 퀵정렬 힙정렬

알고리듬 공부

목록 보기

7/15

정렬알고리듬

목록 안에 저장된 요소들을 특정한 순서대로 재배치하는 알고리듬
사람이 읽기 편하도록 하기위해 && 더 효율적인 알고리듬 사용을 위해 사용됨.
일반적으로 배열 같은 데이터 구조에 저장.
흔히 사용하는 순서: 숫자 순서, 사전 순서
정렬 방향: 오름차순, 내림차순

정렬알고리듬의 안정성

똑같은 key를 가진 데이터들의 순서가 바뀌지 않는가 여부
주로 key-value 쌍으로 이루어진 요소들을 정렬할 때 고려되어야 함.
만약 (이름(key)-반(value))의 데이터가 있다고 가정한다면..!
- 이름순으로 정렬한 후 다시 반 순서로 정렬했을 때 앞의 정렬이 깨지지 않는다면(=순서가 바뀌지 않는다면) 안정적 정렬임.
- 자세한 것은 여기서

대표적인 정렬 알고리듬

주먹구구식
- 버블 정렬(가장 쉬움, 언제라도 구현할 수 있어야 함)
- 선택 정렬(가장 쉬움)
- 삽입 정렬
빠른 정렬
- 퀵 정렬(언제라도 설명할 수 있어야 함, 어떤 언어에서든 기본이 되는 정렬)
- 병합 정렬(이해하는 정도면 충분)
- 힙 정렬(이해하는 정도면 충분)

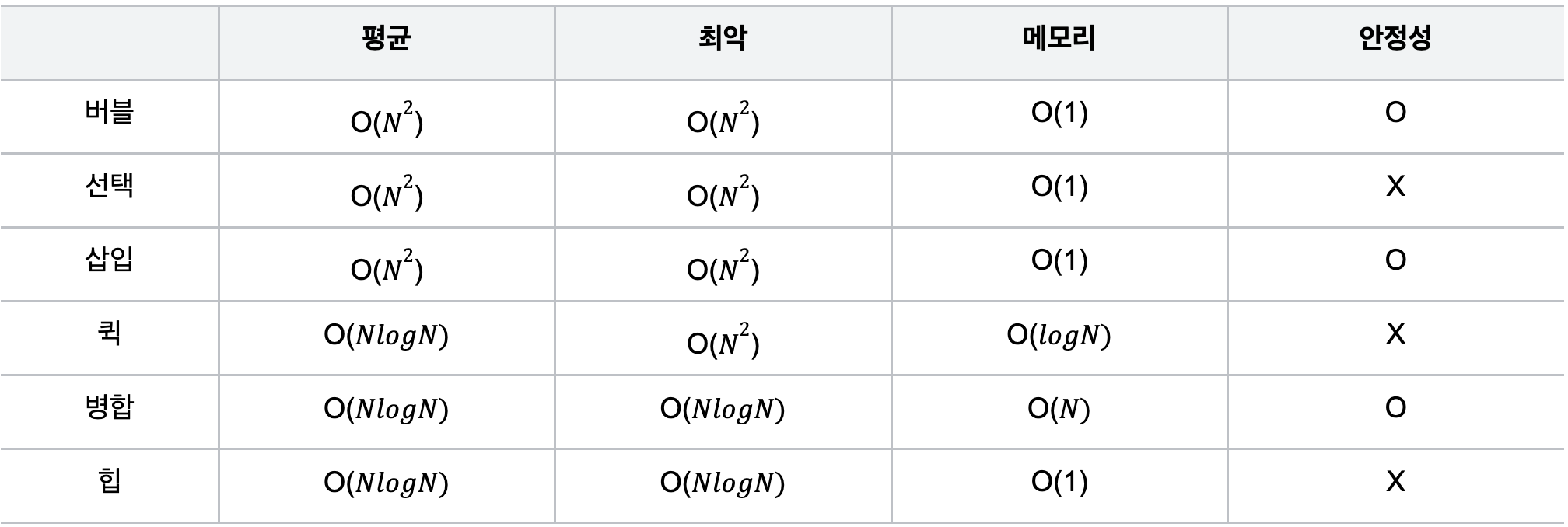
정렬 알고리듬 비교

정렬알고리듬은 아무리빨라도 O(N)보다 느릴 수 밖에 없다..!
- O(N) < O(N log N) < O(N^2)
- 퀵의 경우 스택메모리를 사용

상황에 따른 정렬알고리듬 선택

기본<퀵 정렬>
- C도 qsort()함수를 기본 제공
간단히 구현할 때<버블 정렬>
- 구현이 매우 쉽다.
- 10년 안써도 까먹을 수 없다고 함..!
어떤경우에도 느려지면 안될때<병합 or 힙 정렬>
- 평균은 퀵 정렬보다 느림
- 최악의 경우 여전히 O(NlogN)

버블(bubble) 정렬

이웃요소 둘을 비교해서 올바른 순서로 고치는 과정을 반복
한번 목록을 순회할 때마다 가장 큰 값이 제일 위로 올라감
- 기포가 수면으로 떠오르는 모습을 닮았다고해서 버블정렬
- 큰 기포가 먼저 수면으로 떠오름

선택 정렬

목록을 총 N-1번 훑으면서 다음 과정을 반복
- 첫 번째 요소 0부터 훑으면서 최솟값을 찾아 요소 0과 교환
- 두번째는 요소 1부터 훑으면서 최솟값을 찾아 요소 1과 교환
- 세번째는 요소 2부터 훑으면서 최솟값을 찾아 요소 2와 교환
- N-1번째까지 반복...
최솟값을 찾아 선택한다고 해서 선택 정렬

삽입(insertion)정렬

버블정렬, 선택정렬보다 구현은 아주 조금 힘듦
목록을 차례대로 훑으면서 다음 과정을 반복
- 현재 위치의 요소를 뽑음
- 과거에 방문했던 요소들 중 어디 사이에 넣어야 정렬이 유지되는지 판단
- 그 위치에 삽입
- 삽입으로 인해 다른 요소들을 오른쪽으로 밀어야(shift)할 수도 있음

퀵 정렬

매우 중요한 알고리듬 && 주먹구구식이 아닌 정렬!
실무에서 가장 많이 사용되는 정렬(일반적, 범용적으로 가장 빠름)
진정한 분할 정복 알고리듬
- 모든 요소를 방문함
어떤 값(pivot)을 기준으로 목록을 하위 목록으로 2개 나눔
- 목록을 나누는 기준은 pivot보다 작냐/크냐
- 이 과정을 재귀적으로 반복
- 재귀 단계가 깊어질 때마다 새로운 pivot 값을 뽑음
더 자세히 살펴보면...!
- 재귀적으로 만들기때문에 종료 조건을 설정
  - if(left < right) return
- pivot의 최종 index구하기
  - pivotPos = partition(arr, left, right)
  - pivot의 index를 구하는 방법
    - pivot 값 설정(여기서는 가장 오른쪽 값을 pivot으로 설정함. pivot값 설정하는 방법은 여러가지가 있음. 보통 pivot값을 재귀 depth가 바뀔때마다 랜덤하게 선택한다고 함.)
    - pivot = arr[right]
    - left <= index < right 순회하며 pivot값과 비교 후 pivot보다 큰 값은 pivot 오른쪽으로, pivot보다 작은 값은 pivot 왼쪽으로 정렬함.
```
val i = left
for(j in left until right) {
  if(arr[j] < pivot) {
      swap(arr, i, j)
      ++i
  }
}
```
  - 정렬이 끝났다면 해당 과정을 재귀적으로 반복함.
```
val pivotPos = partition(arr, left, right)
quickSortHelper(arr, left, pivotPos - 1)
quickSortHelper(arr, pivotPos + 1, right)
```
전체 코드

fun quickSort(arr:Array<Int>) {
    return quickSortHelper(arr, 0, arr.size - 1)
}

fun quickSortHelper(arr: Array<Int>, left: Int, right: Int) {
    if(left >= right) return

    val pivotPos = partition(arr, left, right)
    quickSortHelper(arr, left, pivotPos - 1)
    quickSortHelper(arr, pivotPos + 1, right)
}

fun partition(arr: Array<Int>, left: Int, right: Int) : Int{
    val pivot = arr[right]
    var i = left

    for(j in left until right) {
        if(arr[j] < pivot) {
            swap(arr, i, j)
            ++i
        }
    }
    val pivotPos = i
    swap(arr, pivotPos, right)
    return pivotPos
}

fun swap(arr: Array<Int>, a: Int, b: Int){
    val tmp = arr[a]
    arr[a] = arr[b]
    arr[b] = tmp
}

병합 정렬

알고리듬 순서

원본 배열을 정렬된 여러 배열들로 만듦(단, 원본배열을 정렬하면 안됨)
정렬된 배열들을 정렬하며 합치면 끝!

코틀린 코드로 좀 더 자세히 살펴보자면...!
- 재귀적으로 만들것이므로 종료 조건을 설정함
  - if(arr.size <= 1) return
  - 배열의 값이 1개가 남을 때 종료
- 배열의 가운데 index를 구한다
  - mid = arr.size / 2
- 배열을 mid기준 왼쪽, 오른쪽 두개로 나눈다
  - left = ArrayList(arr.subList(0, mid)
  - right = ArrayList(arr.subList(mid, arr.size)
- 위 과정을 재귀적으로 반복하면 배열에 값이 1개밖에 남지않는 정렬된 배열을 얻을 수 있다. (mergeSort는 함수명)
  - mergeSort(left)
  - mergeSort(right)
- 이 후 정렬된 배열들을 다시 정렬해가며 합치면 끝!(mergeArray는 아래 코드 참조)
  - mergeArray(arr, left, right)
전체 코드

fun mergeSort(arr: ArrayList<Int>) {
    if(arr.size <= 1) return

    val mid = arr.size / 2
    val left = ArrayList(arr.subList(0, mid))
    val right = ArrayList(arr.subList(mid, arr.size))

    mergeSort(left)
    mergeSort(right)

    mergeArray(arr, left, right)
}

fun mergeArray(arr: ArrayList<Int>, arr1: ArrayList<Int>, arr2: ArrayList<Int>){
    var i = 0 // arr1의 index를 가리킴
    var j = 0 // arr2의 index를 가리킴
    var k = 0 // arr의 index를 가리킴
    
    while(i < arr1.size && j < arr2.size) {
        // 오름차순 정렬
        if(arr1[i] <= arr2[j]){
            arr[k] = arr1[i]
            ++i
            ++k
        }
        else {
            arr[k] = arr2[j]
            ++j
            ++k
        }
    }

    // arr1.size > arr2.size인 경우
    while( i < arr1.size) {
        arr[k] = arr1[i]
        ++i
        ++k
    }
   
    // arr1.size < arr2.size인 경우
    while(j < arr2.size){
        arr[k] = arr2[j]
        ++j
        ++k
    }
}