해시 알고리듬

해시함수의 정의와 속성

• 해시(hash)는 컴퓨터공학에서 매우 근본이 되는 알고리듬 중 하나

정의

임의의 크기를 가진 값을 고정 크기의 값에 대응시키는 함수
여전히 함수이므로 수학에서의 함수의 정의도 만족해야 함

• 입력(1) : 출력(1) => 함수
• 입력(many) : 출력(1) => 함수
• 입력(1) : 출력(many) => 함수X
  이러한 작동을 결정론적 작동이라고 함.

해시 알고리듬 분류

• (비암호학적) 해시 함수
  • 응용
    • 체크섬(검사합, checksum)
    • 순환중복검사(cyclic redundancy check, CRC)
• 암호학적 해시 함수
• 해시 알고리듬의 다른 속성은 조금씩 달라짐

모든 해시 알고리듬의 속성

• 효율성(efficiency)
• 균일성(uniformity)
• 등...

균일성

• 해시함수의 출력값이 고르게 분포될수록 균일성이 높음.
  • 입력값에대한 출력값이 랜덤하게 분포되어있으면 균일성이 높다고 말함.
• 훌륭한 해시함수는 균일성이 높아야 한다고 함.
  • 출력범위 안의 모든 값들이 동일한 확률로 나와야 함(균등 분포)
  • 이럴경우 해시충돌이 적어 O(1) 해시테이블을 기대할 수 있음.
• 완벽한(perfect)해시함수: 해시 충돌이 전혀 없는 함수
  • 입력값이 매우 제한적일 경우에만 가능

균일성의 측정

• 카이제곱 검정(chi-squared test)을 이용

  • 결과가 0.95 ~ 1.05 사이면 균일한 분포를 가진 해시함수라 봄

• 공식
  

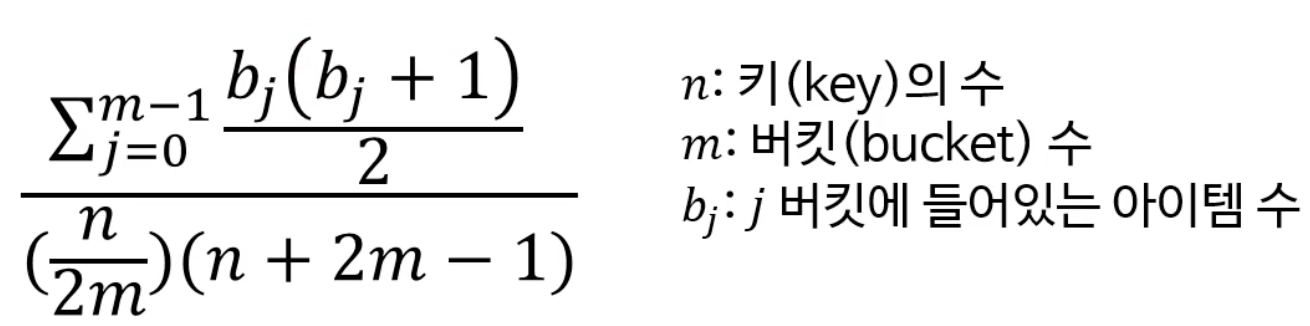
• 균일성을 높일 수 있는 방법

  1. 해시값이 덜 중복되게 버킷 수를 정할 것(소수를 사용)
  2. 완벽한 '눈사태'가 나도록 해시 함수를 설계할 것

눈사태효과!?!(avalanche effect)

• 입력값이 약간만 바뀌어도 출력값이 굉장히 많이 바뀌는 것.
  • 보통 암호학적 알고리듬이 매우 선호하는 효과
  • 알고리듬의 규칙을 쉽게 유추할 수 없음
• 엄격한 눈사태 기준(strict avalanche criterion, SAC)
  • 입력값에서 1비트를 뒤집으면 출력값의 각 비트가 뒤집힐 확률이 50%
  • 이 기준을 충족하는 해시 함수는 분포가 균일할 가능성이 매우 높음

지역민감해시(locality-sensitive hashing)

• 해시 충돌의 최소화 대신 최대화를 목표로 하는 알고리듬
• 비슷한 내용을 가진 데이터끼리 충돌해야 함
• Why??!?
  • 엄청나게 많은 데이터에서 비슷한 것들을 찾는 용도
    • 스팸메일찾기
    • 웹 검색엔진에서 비슷한 문서 추천하기
    • 음원, 사진 등의 저작권 침해 검사
    • 등..

효율성

• 보통 빠른 해시함수를 선호함
• 공간을 더 낭비해도 빠른 접근속도를 선호
• 충돌이 좀 나더라도 더 빠른함수를 선호
• but, 하드웨어 가속이 어려운 해시를 선호하는 경우도 있음
  • 여전히 소프트웨어에서는 빨리 실행되는 걸 선호

암호학적 해시 알고리듬의 추가 속성

• 역상 저항성(pre-image resistance)
• 제2 역상 저항성(second pre-image resistance)
• 충돌 저항성(collision resistance)

비암호학적 해시함수

• 암호학적으로 사용하기에 안전하지 않은 해시함수들.
• 보안적으로 문제없는 용도에 주로 사용
  • 데이터 저장 및 찾기(ex: 해시테이블)
  • 저장/전송 중 생긴 데이터 오류탐지
  • 고유 ID생성
  • 등...
• 이미 이 해시함수의 작동원리는 잘 알고있어야 하는 것들!
• 모든 데이터에 대해 최고의 결과를 보장하는 해시함수는 없다.
• 입력값에 따라 다른 해시함수를 사용하는 확률적 알고리듬은 존재
  • 유니버셜 해싱(universal hashing)
• 따라서 용도에 맞는 해시함수를 사용하는게 중요
  • Java에서 hashCode() 구현을 각 클래스에 맡긴 이유.
• 비트패킹(bit-packing)도 해시함수 사용가능. but, 균일성이 높지 않을 수 있음.

올바른 해시함수를 고르는 법

• 해시함수를 발명하는 경우는 흔치 않기에 보통 이미 존재하는 해시 알고리듬을 사용
  • 많은 사람들이 사용하여 검증한 함수
  • 보통 내가 사용하는 데이터는 아주 특별하지 않다.
• 우리가 집중할 부분
  • 어떤 연산들이 좋은 해시 함수들을 만드는가?
  • 어디에 어떤 해시 함수를 사용해야 하는가?
• 실제로 가지고 있는 데이터로 테스트하면서 측정을 한다.
  • 속도
  • 해시 충돌 수
  • 메모리(보통 크게 중요하지 않음)
  • 균일성 측정(실무에서는 잘 안함)
• 구글님에게 물어본다 ㅎ
  • 내 데이터들이 일반적인 데이터인 경우

LoseLose 해시

• 프로그래밍 책에서 간단히 소개하려고 만든 코드
• 매우 간단하지만 충돌이 많음.
  • 배열1: [A,B,E] -> LoseLose -> 0xC8
  • 배열2: [A,C,D] -> LoseLose -> 0xC8
• 충돌이 자주 일어나는 이유.. 덧셈으로만 해시함수를 만들었기 때문. 해시함수는 이렇게 단순하게도 만들 수 있다는것을 보여줌.

체크섬

• 더하여 검사하는 기법. 여러 데이터로부터 도출한 작은 크기의 데이터 하나.
• 해시함수랑 비슷한 개념
  • 출력값의 크기가 고정되어 있으면 해시 함수
    • ex: 체크섬(xor8)
• 용도: 저장 혹은 전송 중에 발생한 오류를 찾아냄
  • 처음 데이터를 저장할 때 체크섬을 계산해 그것도 저장
  • 나중에 데이터를 읽을 때 다시 체크섬을 계산
  • 처음 저장해둔 체크섬과 다르면 오류가 난 것.
• 체크섬의 사용례
  • 주민등록번호 유효성 검사
    • 존재할 수 있는 번호인지 검사
    • 마지막 숫자는 다음 공식에 따라 계산
      • 11 -(([2,3,4,5,6,7,8,9,2,3,4,5]*[앞 12자리]) % 11)
      • 결과가 10이면 0으로 표기, 11이면 1로 표기
  • 신용카드 번호의 유효성검사
    • 총 16자리
    • 마지막 숫자를 룬(Luhn) 알고리듬으로 만듦
• ISBN의 유효성 검사
  • ISBN 10(국제 표준 도서번호)
    • 각 도서에 붙는 고유한 번호(총 10자리)
    • 마지막 숫자가 체크섬
    • [10,9,8,7,6,5,4,3,2,1]*[앞 9자리, x] ^ 11 == 0 이어야 함.
    • x값이 10이면 X로 표기
    • ISBN 13도 비슷한 규칙이 있음.
• 많이 사용하는 이유? 간단해서!
  • 보통 간단한 산술연산
  • 계산이 빠르고 추가메모리가 거의 불필요
    • 네트워크 프로토콜에서 사용
    • 하드웨어로도 구현하기 쉬움
  • 단, 모든 오류를 찾지는 못함
    • xor8은 'AB'와'BA'의 체크섬이 같음
    • 위치까지 고려한 다른 알고리듬도 존재(예: Adler-32, CRC)
• 체크섬은 데이터가 바뀐지만 확인함.
• 데이터 복구를 지원하는 것도 있음
  • 오류정정코드(error-correcting code, ECC) 등..
  • 보통 어느정도까지만 복구가능
• 체크섬과 미러사이트
  • 유용한 프로그램으로 많은 사람들이 다운로드 -> 한 웹사이트에서 트래픽 감당 X -> 다른 웹사이트에서 대신 파일을 호스팅
  • 미러사이트에서 내 프로그램에 스파이웨어를 넣으면?
    • 그걸 위해 내 웹사이트에 체크섬 값을 공개해 놓음.
    • 사용자는 미러사이트에서 받은 파일에 체크섬 알고리듬을 돌림
    • 그 둘이 일치하지않으면 누군가 변조한 프로그램
  • 미러사이트에 공개해 놓은 체크섬 값은 아무 도움안됨.
• 패리티 비트(parity bit)
  • 이진수로 저장된 데이터에 추가하는 1비트차리 체크섬
  • 보통 1바이트 단위로 많이 사용(7비트 데이터 + 1버트 패리티)
• 짝수 패리티와 홀수패리티로 나뉨
  • 패리티 포함 모든 비트를 더하면 그 결과가 짝수 or 홀수가 되어야 함
    • 데이터: 000 0000 (1비트 개수: 0)
      • 홀수 패리티: 1000 0000
      • 짝수 패리티: 0000 0000
    • 데이터: 010 1100 (1비트 개수: 3)
      • 홀수 패리티: 0010 1100
      • 짝수 패리티: 1010 1100
    • 데이터: 111 1111 (1비트 개수: 7)
      • 홀수 패리티: 0111 1111
      • 짝수 패리티: 1111 1111
• 순환중복검사(cyclic redundancy check)
  • 체크섬 알고리듬중 하나
  • 다항식의 나머지 연산을 이용하여 검사값을 만듦
    • 검사값은 보통 고정된 길이
    • 따라서 CRC 함수를 해시 함수로 사용하기도 함
  • 역시 이진수 하드웨어에서 구현하기 쉬움
    • 심지어 최신CPU는 CRC-32C 명령어를 탑재!
• CRC의 다항식과 이름
  • 다항식의 최고차항에 따라 CRC에 사용하는 비트수가 달라짐
    • 각 항의 계수는 1 or 0
    • 최고차항의 계수는 언제나 1
  • 다음 다항식을 이진수로 표현하면? x^3 + x + 1
    • 1011(총 4비트) 줄이면? 011
  • 이건 CRC-3-GSM에 사용하는 다항식
• CRC-3-GSM 계산 예
  1. 원본 메세지: 10101001011001
  2. (다항식 비트 수 - 1)만큼 0을 추가
  • 10101001011001 000
  3. 위의 원본값과 다항식 비트 1011을 XOR연산
  • 10101001011001 000 XOR 1011 = 00011001011001 000
  4. 1비트 shift하여 XOR계산을 반복함. 단, 맨 앞의 bit가 1이라면 패스함. 최종목적은 모든 비트를 0으로 만드는 것.
  5. 최종결과: 00000000000000 001 여기서 001이 체크섬임.
  6. 검증법
     1. 읽은 메세지에 검사값을 붙임. 이 경우 001을 비트 뒤에 추가함.
     2. 1011과 XOR하여 0이 나오면 무결성 보장됨. 다르면? 오류가 있음.
• 흔히 사용하는 CRC알고리듬들
  • CRC-8
  • CRC-16
  • CRC-32
  • CRC-64
• 각 알고리듬에 사용하는 다항식은 위키 참조.

본 내용은 Udemy의 알고리듬 및 자료구조(Java)강의를 듣고 정리한 내용입니다.