확률분포

대학 진학을 앞둔 고등학교 3학년 학생의 경우를 생각해보자. 자신의 수능 점수가 상위 몇 %에 속하냐에 따라 지원 대학과 학과가 결정된다. 그러므로 자신의 수능점수 보다는 전체 학생들의 수능점수 분포에서 자신의 점수가 어디에 위치하고 있는지를 아는 것이 더 중요하다. 전체 학생의 수능점수분포와 같이 수능점수 별 학생 수의 (혹은 확률의) 분포를 확률 분포라 한다. 이러한 확률 분포는 지원 대학을 결정하는 고등학교 3학년 학생들에게 필수적인 정보이다.

# 확률변수의 개념

동전을 던지거나 주사위를 던지는 실험을 하면 결과가 다양하게 나타난다. 동전의 경우는 앞면이나 뒷면, 주사위의 경우는 {1, 2, ... , 6} 중 하나의 숫자가 위에 나타난다. 이렇게 다양한 형태의 실험 결과를 일반화된 방식으로 표현할 필요가 있다. 이런 방식 중 하나가 확률변수이다. 다음은 확률변수(random variable)의 정의이다.

확률변수: 확률실험 결과에 수치를 부여하는 함수로, 일반적으로 $X, Y, Z$ 등 영문 대문자로 표기한다.

이 정의에 따르면 확률변수는 1) 결과에 수치가 부여되고, 2) 실험 결과가 확률적으로 발생된다는 두 조건을 만족해야 한다.

예를 들어, '주사위를 던질 때 위에 나온 숫자'는 결과가 {1, ... , 6} 중의 하나이므로 수치에 해당하고, 결과 값들이 확률적으로 발생하므로 위의 확률변수의 개념에 부합한다. 반면 '동전을 던질 때 나오는 앞면 혹은 뒷면'은 확률변수의 개념에 부합하지 않는다. 결과가 숫자가 아닌 {앞면, 뒷면} 중 하나이기 때문이다. 확률변수로 만들려면 {앞면, 뒷면} 대신 {1(앞면인 경우), 0(뒷면인 경우)} 등의 수치를 부여하면 된다. '어제의 종합지수'는 결과가 수치이나, 확률 실험이 필요치 않은 이미 확정된 숫자이기에 확률변수가 아니다. 반면 '내일의 종합지수'는 결과가 수치이고, 상승폭/하락폭 등의 확률 분포에 근거하여 지수 값의 분포를 얻어내므로 확률변수이다.

# 이산확률변수와 연속확률변수

1. 이산확률변수와 연속확률변수의 구분

확률변수는 이산확률변수와 연속확률변수로 나뉜다. 이산확률변수(discrete random variable)는 확률변수가 취할 수 있는 값의 수를 셀 수 있으나, 연속확률변수(continuous random variable)는 확률변수가 취할 수 있는 값의 수를 셀 수 없다. 대신, 취할 값을 구간으로 표시한다.

이산확률변수와 연속확률변수의 사례는 각각 다음과 같다.

이산확률변수	연속확률변수	연속확률변수의 구간 표현 예시
1) 주사위를 던질 때 위에 나오는 숫자	1) 어떤 주식의 하루 주가상승률	[-30% ~ +30%]
2) 주사위를 10번 던질 때 짝수가 나올 횟수	2) 어떤 회사의 매출성장률	[-100% ~ 1,000%]
3) 어느 개인 병원의 하루 환자 수	3) 우리나라의 연간 강수량	[0mm ~ 2,500mm]

2. 이산확률변수의 확률분포

확률변수가 취할 수 있는 수치와 이들 수치가 발생할 확률을 표나 그래프로 표현한 것을 확률분포(probability distribution)라 한다. 예를 들어, 동전을 한 번 던져 앞면이 나오면 '1'을 부여하고 뒷면이 나오면 '0'을 부여하는 경우의 확률분포는 다음과 같이 표로 나타낼 수 있다.

x	0	1
확률	1/2	1/2

확률분포를 그래프로 나타내면 다음과 같다.

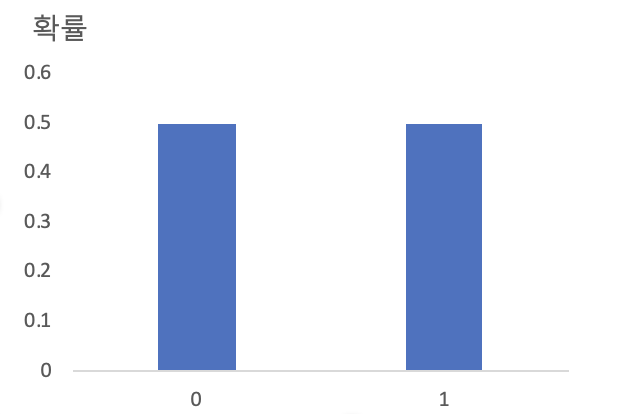
확률분포를 수식으로도 표현할 수 있는데, 이를 확률함수(probability function)라 한다.
이 함수는 $P(X=x)$로 표기하는데, 이산확률변수 $X$가 $x$라는 값을 취할 때의 확률을 나타낸다.
위의 동전던지기의 예는 $P(X=0)=1/2, P(X=1)=1/2$이다.

확률함수의 표기
$P(X=x) = ...$

[확률분포의 표현 정리]
확률분포는 표, 그래프, 수식으로 표현이 가능하다.
표로 표현하는 경우를 확률분포표, 그래프로 표현하는 경우를 확률분포 그래프,
수식으로 표현하는 경우를 확률질량(밀도)함수라 한다.

이산확률변수의 확률함수를 확률질량함수(probability mass function)라 부르기도 한다.
$X=x$ 일 때의 확률이 명확히 어떤 (질량) 값으로 표현되기 때문이다.

이산확률분포가 $k$개의 값($x_{1}, x_{2}, ... , x_{k}$)을 확률적으로 가질 때,
확률분포는 다음의 특성을 가진다.

[이산확률분포의 특성]

• $0 \le P(X=x_{i}) \le 1, \;\;i=1, ... , k$
• $\sum_{i=1}^{k}P(X=x_{i}) = 1$

첫 번째 특성은 확률이 0과 1사이의 값이고, 두 번째 특성은 확률의 총합이 1이라는 뜻이다.

3. 연속확률변수의 확률분포

이산확률변수의 확률분포는 취할 수치와 발생할 확률을 표나 그래프로 표현할 수 있다. 반면에 연속확률변수는 일정 구간 내의 어떤 실수도 취할 수 있으므로 연속확률변수의 확률분포를 표나 그래프로 표현할 수 없다.

또 하나 유의할 점은 연속확률변수가 특정한 값을 취할 확률이 0, 즉 $P(X=x) = 0$ 이라는 점이다. 연속확률변수가 취할 수 있는 값의 수가 무한대이므로 특정한 값을 취할 확률은 무한대 중 하나, 1/$\infin$, 즉 0이다. 예를 들어, 어느 지역의 강수량이 1,000~2,000mm 사이에 분포할 때, 강수량이 1,500mm 일 확률은 0이다.

강수량이 어떤 값을 가질 확률은 0이지만 강수량이 어떤 구간에 존재할 확률은 0이 아니다. 앞의 예에서처럼 어느 지역의 강수량이 1,000~2,000mm 사이에 분포할 때, 강수량이 1,000~2,000mm 사이에 존재할 확률은 1이다. 같은 방식으로 강수량이 1,500mm~1,600mm 사이에 있을 확률은 일반적으로 0이상이다. 이 때의 확률은 $P(1,500 \le X \le 1,600)$ 로 표현하는데, 이를 시각화하여 면적으로 해석하려면 확률밀도라는 개념을 먼저 도입해야 한다. 아래의 그림은 확률변수 $X$ 가 취할 수 있는 값 각각에 대응하는 확률밀도(probability density) 값들의 예이다. 또 아래 그램에서와 같이 확률변수와 확률밀도의 관계를 나타낸 함수를 확률밀도함수(probability density function)라 하며, 이를 $f(x)$로 표기한다. 확률밀도는 확률과 다르다는 점에 유의한다. 예를 들어, 강수량이 1,500mm 일 확률은 0이나 확률밀도는 아래 그림에서 볼 수 있는 것처럼 0이 아닌 양(+)의 값을 갖는다. 즉, 아래 그림에서처럼 $P(X=1,500mm)=0$ 이나 $f(1,500mm)>0$ 이다.

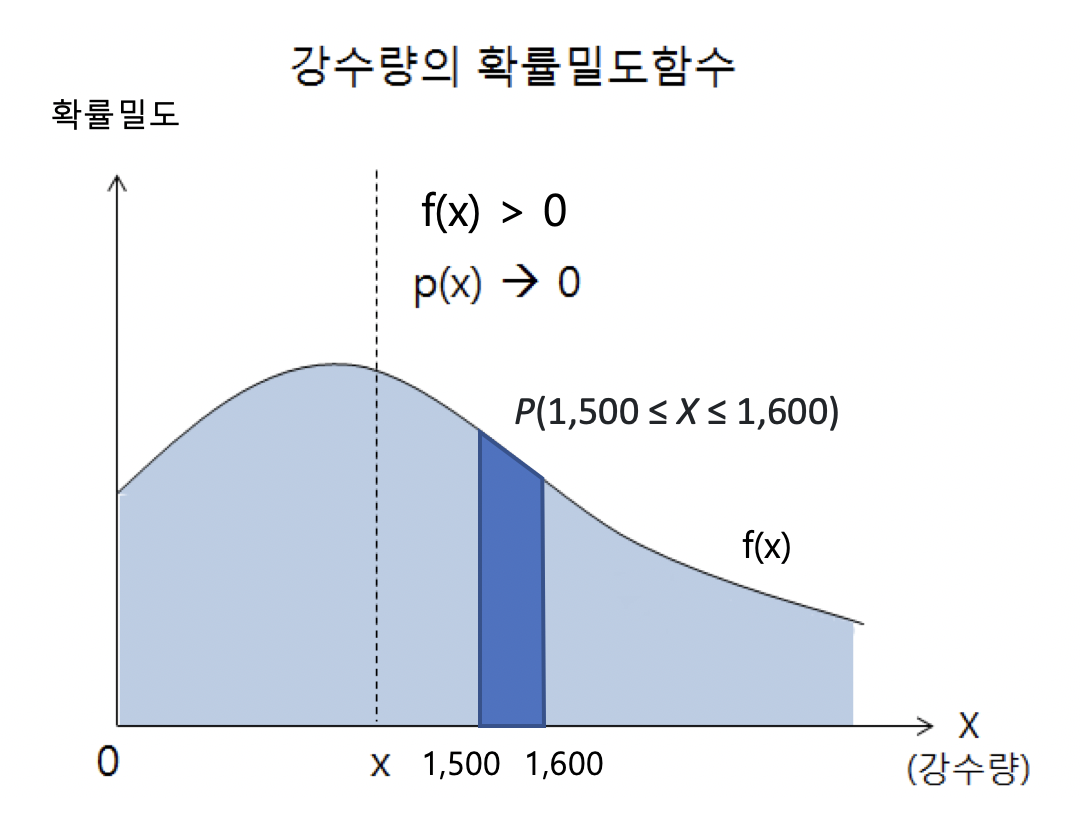
$P(1,500 \le X \le 1,600)$ 의 값은 위의 그림에서 강수량이 1,500mm 와 1,600mm 사이에 있는 확률밀도함수(이 그림에서는 $f(x)$) 아래에 있는 파란색 부분의 면적으로 표현한다. 즉, $\int_{1500}^{1600}f(x)dx$ 이다. 또한 $P(X=1500)=0$ 이고, $P(X=1600)=0$ 이므로 $P(1,500 \le X \le 1,600) = P(1,500 \lt X \le 1,600) = P(1,500 \le X \lt 1,600) = P(1,500 \lt X \lt 1,600)$ 이 성립한다.

연속확률변수 $X$가 구간 $[a, b]$ 에서 정의될 때, 확률밀도함수는 다음의 특성을 갖는다.

[확률밀도함수의 특성]

• 구간 $[a, b]$ 에 존재하는 어떤 $x$에 대해 $f(x) \ge 0$
• $\int_{a}^{b}f(x)dx = 1$

첫 번째 특성은 확률밀도가 음(-)을 취하지 않는다는 뜻이며, 두 번째 특성은 확률밀도함수의 전체 면적이 1이라는 의미이다.

이산확률변수의 경우 특정한 점의 확률은 1보다 클 수 없지만, 연속확률변수의 경우에는 확률밀도가 1보다 클 수 있다는 점에 유의하자. 예를 들어, 연속확률변수 $X$가 구간 [1, 1.5]에 존재하고, 확률밀도함수 $f(x)=\alpha$ 라 가정해 보자. 위의 두 번째 특성에 의해 $\int_{1}^{1.5} \alpha dx = 1$ 이 되고, 이를 만족하는 $\alpha = 2.0$ 이 된다. 따라서, 한 점 $x$ 에서의 확률밀도 즉, $f(x)$ 의 값은 1 보다 클 수 있다.

4. 확률변수의 확률계산

확률변수가 2와 5 사이일 확률은 $P(2 \le X \le 5)$ 로 표현되나, 계산하는 방법은 확률변수가 이산인가 연속인가에 따라 다르다.

• 이산확률변수의 경우: $P(2 \le X \le 5) = \sum_{i=2}^{5}P(X=i)$
• 연속확률변수의 경우: $P(2 \le X \le 5) = \int_{2}^{5}f(x)dx$

이번에는 $P(2 \lt X \le 5)$ 를 구해보자. 예를 들어, 주사위를 던질 경우 $P(2 \le X \le 5)$ 는 $X$ 가 2, 3, 4, 5 중 하나가 나올 확률을 의미하는 반면, $P(2 \lt X \le 5)$ 는 3, 4, 5 중 하나가 나올 확률을 뜻한다. 그러나 확률변수가 연속이라면 $P(X=2)=0$ 이므로 $P(2 \lt X \le 5)$ 는 $P(2 \le X \le 5)$ 와 동일하다. 즉, 정리하면 다음과 같다.

• 이산확률변수의 경우(주사위를 던지는 경우): $P(2 \lt X \le 5) = \sum_{i=3}^{5}P(X=i)$
• 연속확률변수의 경우: $P(2 \lt X \le 5) = \int_{2}^{5}f(x)dx$

5. 누적분포함수

누적분포함수(cumulative distribution function)는 확률변수 $X$가 특정한 값 $x$ 이하일 확률을 함수로 나타낸 것으로 $F(x)$ 로 표기한다. 즉, $F(x)=P(X \le x)$. 누적분포함수는 확률변수가 이산인 경우와 연속인 경우 모두 동일하게 $F(x)$로 표기된다.

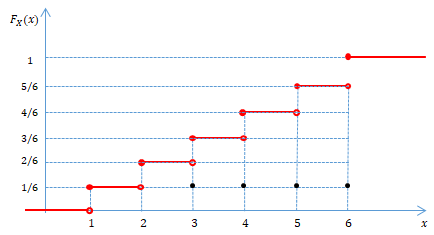
주사위를 던져 나온 숫자를 $X$라 할 때, 누적분포함수 $F(x)$는 다음과 같다.
주사위를 한 번 던질 때 4 이하가 나올 확률은 $F(4) = P(X \le 4) = 2/3$ 이다.

연속확률변수가 [0, 10]의 구간에서 일정한 확률밀도인 1/10를 가질 때, 누적분포함수 $F(x)$ 다음과 같다.
$X$ 의 값이 6 이하의 값이 나올 확률은 $F(6) = P(X \le 4) = \int_{0}^{6} \frac{1}{10} dx = 3/5$ 이다.

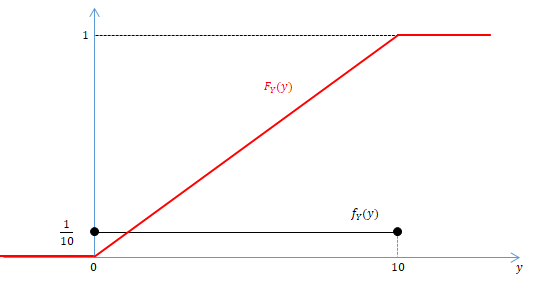
위의 두 그림에서 볼 수 있는 것처럼 누적분포함수의 모양은 확률변수가 이산이냐 연속이냐에 따라 다르다. 이산이면 누적확률에 불연속인 점프가 존재하나, 연속이면 점프없이 매끄럽다.

# 확률변수의 기댓값과 분산

1. 기댓값

어느 회사의 예상 매출액을 [260억, 360억] 사이라는 구간으로 표현할 수 있지만, 310억원이라고 말하는 것이 좀 더 명확한 표현이다. 즉 예상되는 값의 대푯값을 알려주는 것이 예상되는 구간을 알려주는 것보다 빠르고 쉽게 이해시킬 수 있다. 이 예상되는 값의 평균을 기댓값이라 한다.

기댓값이란 확률변수의 발생 가능한 모든 결과에 대해 가중평균한 값이다.
확률변수 $X$ 의 기댓값은 $E(X)$로 표기한다.

1.1 이산확률의 기댓값

$X$가 $n$개의 값을 취할 수 있다면 이산확률변수의 기댓값은 다음과 같이 계산한다.

이산확률변수의 기댓값: $E(X)=\sum_{i=1}^{n}P(X=x_{i}) \cdot x_{i}$

주식 $ABC$의 내일 주가는 15,000원, 18,000원, 20,000원으로 예상된다. 그리고 이들의 확률은 각각 0.2, 0.3, 0.5이다. 내일 $ABC$의 주가의 기댓값을 구해보자.

먼저 확률변수 $X$를 주식 $ABC$의 내일 주가라 하자. $X$의 확률분포표를 작성하면 다음과 같다.

$x$	15,000	18,000	20,000
$P(X=x)$	0.2	0.3	0.5

기댓값 공식을 이용하여 계산하면 다음과 같다.
$E(X) = 0.2 \cdot 15,000 + 0.3 \cdot 18,000 + 0.5 \cdot 20,000 = 18,400$

1.2 연속확률변수의 기댓값

연속확률변수의 기댓값은 다음과 같이 계산한다.

연속확률변수의 기댓값: $E(X) = \int_{-\infin}^{+\infin}x \cdot f(x) dx$

연속확률변수 $X$가 다음과 같은 확률밀도함수를 가진다고 할 때, 확률변수 $X$의 기대값을 구해보자.

$f(x)= \begin{cases} 1/5, & 1 \le x \le 6 \\ 0, & otherwise \\ \end{cases}$

확률변수 $X$의 기댓값을 위 공식에 대입하면 다음과 같이 계산된다.

$E(X) = \int_{1}^{6}x \cdot 1/5 dx = 3.5$

2. 분산

분산은 흩어진 정도를 측정하는 툴이지만 확률변수에 대한 분산은 불확실성의 정도를 나타낸다고 해석할 수 있다. 확률변수 $X$의 분산은 $Var(X)$ 나 $\sigma_{X}^{2}$ (또는 $\sigma^{2}$) 로 표기한다.

확률변수의 분산: $Var(X) = E[(X-E(X))^{2}] = E[X^{2}] - E[X]^{2}$

$X$의 분산은 확률변수가 이산인가 연속인가에 따라 다르게 계산한다.

$Var(x)=E[(X-E(X))^{2}] = \begin{cases} \sum_{i} P(X=x_{i}) \cdot (x_{i}-E(X))^{2}, &X가 이산인 경우 \\ \int_{-\infin}^{+\infin} (x-E(X))^{2} \cdot f(x), &X가 연속인 경우 \\ \end{cases}$

위의 주식 $ABC$의 내일 주가의 기댓값 $E(X)=18,400$ 이였다.
이를 이용하여 $(x-E(X))^{2}$ 값과 이 값의 확률을 표로 나타내면 다음과 같다.

$(x-E(X))^{2}$	$(15,000-18,400)^{2}$	$(18,000-18,400)^{2}$	$(20,000-18,400)^{2}$
$P(X=x)$	0.2	0.3	0.5

따라서, 분산 $Var(X)$ 는 다음과 같이 계산할 수 있다.
$Var(X) = 0.2 \cdot (15,000-18,400)^{2} + 0.3 \cdot (18,000-18,400)^{2} + 0.5 \cdot (20,000-18,400)^{2} = 3,640,000$

3. 기댓값과 분산의 특성

먼저 기댓값은 다음과 같은 특성을 지니고 있다.

기댓값의 특성
$X$와 $Y$는 확률변수이고, $a$와 $b$는 상수이다.
1) $E(a) = a$
2) $E(aX) = aE(X)$
3) $E(X + b) = E(X) + b$
4) $E(aX + bY) = aE(X) + bE(Y)$

기댓값은 선형의 특성을 지니므로, 위의 식이 쉽게 이해가 될 것이다.

다음으로 분산은 다음과 같은 특성을 지니고 있다.

분산의 특성
$X$와 $Y$는 확률변수이고, $a$와 $b$는 상수이다.
1) $Var(a) = a$
2) $Var(aX) = a^{2}Var(X)$
3) $Var(X + b) = Var(X)$
4) $Var(aX + bY) = a^{2}Var(X) + b^{2}Var(Y) + 2abCov(X,Y)$

$Var(aX)=E[(aX-E(aX))^{2}] = E[(aX-aE(X))^{2}] = E[a^{2}(X-E(X))^{2}] = a^{2}Var(X)$ 가 된다.
분산은 흩어진 정도이므로 $X$ 가 취할 수 있는 모든 값에 $b$ 만큼을 옮기더라도 분산은 변하지 않는다. 즉, $Var(X+b) = Var(X)$
분산 $Var(X) = E(X^{2}) - E(X)^{2}$ 이므로 $Var(aX+bY)$ 를 이에 적용하면 다음과 같이 정리할 수 있다. (여기서, 공분산 $Cov(X,Y)=E[(X-E(X))(Y-E(Y)] = E(XY)-E(X)E(Y)$ 로 정의된다.)

$\begin{aligned} Var(aX+bY) &= E((aX+bY)^{2}) - (E(aX+bY))^{2} \\ &= a^{2}E(X^{2}) + b^{2}E(Y^{2}) +2abE(XY) - a^{2}E(X)^{2} - b^{2}E(Y)^{2}-2abE(X)E(Y) \\ &= a^{2}(E(X^{2})-E(X)^{2}) + b^{2}(E(Y^{2})-E(Y)^{2}) + 2ab(E(XY)-E(X)E(Y)) \\ &= a^{2}Var(X) + b^{2}Var(Y) + 2abCov(X, Y) \end{aligned}$

# 공분산

공분산(Covariance)이란 두 확률변수 $X$와 $Y$의 변동 방향과 강도를 나타낸다. 공분산은 다음과 같이 정의한다.

$X$와 $Y$의 공분산
$\begin{aligned} Cov(X, Y) &= E[(X-E(X))(Y-E(Y))] \\ &= E(XY)-E(X)E(Y) \end{aligned}$

$X$와 $X$의 공분산을 구하면 $Cov(X, X)=E[(X-E(X))(X-E(X))]=E[(X-E(X))^{2}] = Var(X)$ 가 된다. 즉 분산은 공분산의 특수한 한 형태로 볼 수 있다.

아래 그림은 확률변수 $X$와 $Y$로부터 얻어진 관찰점 $(x, y)$ 들을 시각적으로 표현한 것이다. 각각의 점(그림에서는 "x"로 표시)들은 관찰점들을 의미하고, $\bar{x}, \bar{y}$는 각각 확률변수 $X$와 $Y$의 기댓값 $E(X), E(Y)$이다. 아래 그림의 왼쪽에서 볼 수 있는 것처럼 $(\bar{x}, \bar{y})$ 를 원점으로 1, 3사분면에 있는 점들은 $(x-\bar{x})(y-\bar{y})$ 의 값이 양(+)이다. 반대로 $(\bar{x}, \bar{y})$ 를 원점으로 2, 4 사분면에 있는 점들은 $(x-\bar{x})(y-\bar{y})$ 의 값이 음(-)이 된다. 따라서 $(\bar{x}, \bar{y})$ 를 원점으로 1, 3 사분면에 있는 점들은 공분산 값에 양(+)의 영향을 주고, $(\bar{x}, \bar{y})$ 를 원점으로 2, 4 사분면에 있는 점들은 음(-)의 영향을 준다.

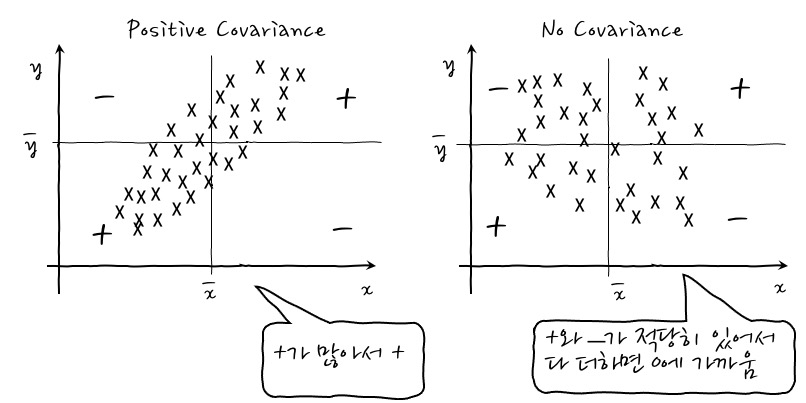
위의 그림의 왼쪽처럼 1, 3 사분면의 점들이 2, 4 사분면의 점들보다 많으면, 즉 오른쪽으로 기울어진 분포이면 공분산은 양(+)이 되고, 반대로 2, 4분면의 점들이 1, 3 사분면의 점들보다 많으면, 즉 왼쪽으로 기울어진 분포이면 공분산은 음(-)이 된다. 반면 위 그림의 오른쪽처럼 점들이 1~4분면에 골고루 퍼져 있다면 공분산은 0이 된다.

다음으로 공분산의 절대값 크기를 살펴보자.
공분산의 절대값은 모든 $(x, y)$에 대하여 $(x-\bar{x})(y-\bar{y})$ 값들의 부호가 서로 동일할수록, 그리고 이들의 값이 크면 클수록 커진다. 부호가 모두 동일하기 위해서는 아래 그림의 "강함"에 해당하는 형태로, 1) 관찰점을 대변하는 직선을 그리고 2) 관철점들이 이 직선에 가까이에 있어야 한다. 반대로 관찰점들이 이 직선에 멀리 있을수록 점들이 서로 다른 부호를 가지게 되어 공분산의 절대값이 작아진다. 아래 그림의 "약함"에 해당하는 형태이다. 관찰점을 대변하는 직선에 점들이 가까이 몰려있고 관찰점 분포의 너비가 동일하다면, 이 직선의 기울기가 공분산의 절대값에 영향을 미친다. 즉, 동일한 형태의 관찰점 분포라면 직선의 기울기가 $\pm 1$일 때 공분산의 절대값이 커진다. 왜냐하면 $(x-\bar{x})(y-\bar{y})$ 의 값이 최대가 되려면 $|(x-\bar{x})| = |(y-\bar{y})|$ 여서 $\frac{(x-\bar{x})}{(y-\bar{y})}=\pm1$ 일 때 공분산의 절대값이 최대가 되기 때문이다. 관찰점들이 대변하는 직선의 기울기가 동일할 때는 이 직선을 기준으로 점들이 길게 늘어져 있을수록 공분산의 절대값은 커진다. 확률변수 "X"와 "Y"의 단위가 kg, cm 일 때보다 g, mm 로 변경해 측정한 공분산이 훨씬 크다는 것으로 이를 확인할 수 있다.

펀드가 2개의 주식 ($A, B$)로 구성되어 있고, 이들의 기대 수익률과 분산은 다음과 같다.

주식명	A	B
기대수익률	20%	10%
분산	100	400

$X$와 $Y$를 주식 $A$와 $B$의 수익률이고, Cov(X, Y)=150 이라 하자. $A$와 $B$에 대한 투자 비율이 1:3 이라면 이 펀드의 수익률은 $R_{p}=0.25X + 0.75Y$ 로 표현된다. 이 펀드의 기대수익률과 위험도는 어떻게 될까?

먼저 펀드의 기대수익률은 $E(R_{p})=E(0.25X + 0.75Y) = 0.25E(X) + 0.75E(Y) = 0.05 + 0.075 = 0.125 = 12.5\%$ 이다.

다음으로 이 펀드의 위험도 즉 분산을 계산해보자. $Var(R_{p})=Var(0.25X+0.75Y) = 0.25^{2} \cdot Var(X) + 0.75^{2} \cdot Var(Y) + 2 \cdot 0.25 \cdot 0.75 \cdot Cov(X,Y) = 287.5$ 이다.

# 상관관계

1. 상관계수와 공분산

공분산과 유사한 지표로 상관계수(correlation coefficient)가 있다. 상관계수는 $\rho$ 로 표기하며, 다음과 같이 정의한다.

$X$와 $Y$의 상관계수: $\rho = \frac{Cov(X, Y)}{\sigma_{X} \cdot \sigma_Y}$, $-1 \le \rho \le 1$

이 정의에서 알 수 있듯이 $\sigma_{X}$와 $\sigma_{Y}$의 부호가 모두 양(+)이므로 상관계수의 부호는 공분산의 부호와 일치한다. 물론 상관계수가 0이면 공분산도 0이다. 상관계수가 공분산과 비슷한 점이 많지만 다른 점도 있다.

먼저 상관계수는 측정 단위에 관계없이 일정하다. 예를 들어, 키와 몸무게를 cm와 kg으로 측정한 자료를 사용하여 계산한 결과 Cov($X, Y$)=200, $\sigma_{X}=15, \sigma_{Y}=40$ 이 나왔다. 여기서 $X$와 $Y$는 각각 키와 몸무게이다. 이 때의 상관계수 $\rho = 200/(15\cdot40) = 1/3$이 된다. 만약 이 자료의 측정 단위를 mm와 g으로 바꾼 후 공분산과 표준편차를 구해보면 각각 Cov($X, Y$)=$200\times10^4$, $\sigma_{X}=150, \sigma_{Y}=40\times10^{3}$ 이 된다. 따라서 이 때의 상관계수 $\rho =200\times10^{4}/(150\times 40\times10^{3}) = 1/3$ 로 변함이 없다.

공분산은 관찰점을 대변하는 직선의 기울기가 $\pm 1$ 에 가까울수록 그리고 이 직선을 따라 점들이 길게 늘어져 있을수록 공분산의 절대값이 커지게 됨을 앞에서 배웠다. 반면 상관계수는 공분산값을 $\sigma_{X}$와 $\sigma_{Y}$로 나누어 정규화한다. 따라서, 관찰점을 대변하는 직선의 기울기가 다르더라도 관찰점들의 분포가 직선을 따라 길게(혹은 짧게) 분포되어 있더라도 상관계수 값이 동일한 경우가 존재한다. 좀 더 구체적으로 말하면 관찰점을 대변하는 직선에 관찰점들이 가까이 혹은 멀리 분포되어 있는지가 상관계수값을 결정한다. 생각해보면, 확률변수 $U=\frac{X-E(X)}{Var(X)}$라 정의할 때, $U$는 $X$를 표준정규분포로 변환하는 식과 같다. 즉, $E(U)=0, Var(U)=1$이 된다. 따라서, 상관계수는 공분산의 정규화로 볼 수 있다.

앞에서 살펴본 것처럼 공분산과 상관계수 모두 두 확률변수의 변동방향과 강도를 나타내는 지표이나 위에서 이야기 나눈 것처럼 상관계수가 좀 더 안정적인 지표이다. 상관계수의 값의 분포가 [-1, +1] 이여서 상관계수 값에 따라 두 확률변수의 상관관계를 어느 정도 명확히 이야기할 수 있지만 공분산은 상하한이 없어 두 확률변수의 관계를 명확히 집어내기 어렵다.

2. 상관계수와 비선형관계

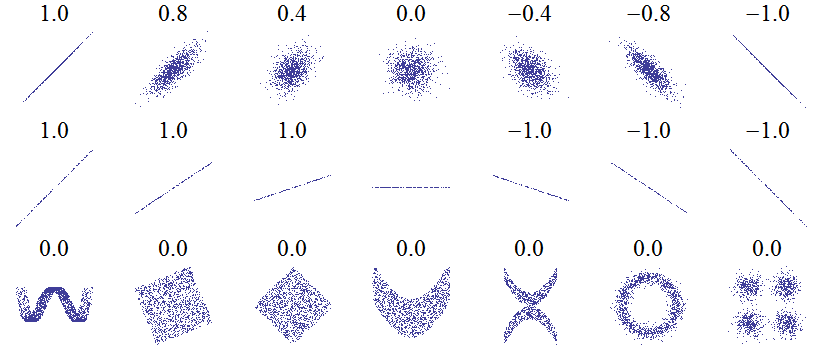
아래 그림은 확률변수 $X$와 $Y$로부터 얻어진 관찰점 $(x, y)$ 들의 여러 모양(형태)에 따른 상관계수 값을 나타낸다. 아래 그림의 첫 번째와 두 번째 줄의 그림에서처럼 상관계수는 두 확률변수의 선형적 관계를 측정하는 도구이다. 오른쪽으로 기울어진 직선 형태일수록 +1에 가까워지고 왼쪽으로 기울어진 직선 형태일수록 -1에 가까워진다. 아래 그림의 두 번째 줄에서 볼 수 있는 것처럼 관찰점들이 관찰점을 대변하는 직선에 몰려있는 정도가 동일하다면 기울기와 관계없이 상관계수의 값은 모두 동일하다.

아래 그림의 마지막 줄은 $X$와 $Y$가 뚜렷한 관계가 있음에도 불구하고 상관계수가 0인 경우들이다. 그 이유는 상관계수가 선형관계의 정도만을 측정할 뿐 비선형관계의 정도를 측정하지 못하기 때문이다.

3. 공분산(또는 상관계수)와 독립

독립은 확률적으로 두 확률변수 $X$와 $Y$가 서로 영향을 주지 않는다는 뜻이므로 선형/비선형과 관계없이 공분산(또는 상관계수)이 0이다. 그러나 공분산은 두 확률변수 간의 선형적인 관계만 측정하므로 공분산이 0이라고 해서 두 확률변수가 독립인 것은 아니다.

독립 $\to$ 공분산 0
독립 $\nleftarrow$ 공분산 0

예를 들어, 두 확률변수 $X$와 $Y$가 다음과 같은 확률값을 가질 때 공분산과 독립여부를 확인해보자.

($x, y$)	확률	$(x-E(X))(y-E(Y))$
(-1, 1)	1/3	(-1-0)(1-2/3)=-1/3
(0, 0)	1/3	(0-0)(0-2/3)=0
(1, 1)	1/3	(1-0)(1-2/3) = 1/3

먼저 공분산 Cov($X, Y$) = -1/3 + 0 + 1/3 = 0 이다.
반면 $P(-1, 1) = 1/3$ 이고, $P(-1) = 1/3, P(1)=2/3$ 으로, $P(-1,1) \ne P(-1)P(1)$ 이므로 두 확률변수 $X$와 $Y$는 독립이 아니다.

4. 상관계수와 인과관계

두 확률변수의 상관계수가 높다면 선형관계의 정도가 매우 높다는 뜻이나 두 확률변수 간의 인과관계가 있다는 것을 의미하지는 않는다. 예를 들어, 검색엔진 네이버에는 "국민은행"과 "우리은행"이 매일 비슷한 비율로 검색이 유입된다. 이 둘은 많은 사람들이 자주 검색하는 검색어이기에 매일 일정한 비율을 유지한다. 따라서 이 두 검색어의 상관계수는 매우 높지만 두 검색어 간의 인과관계가 성립하지는 않는다. 인관관계를 설명하기 위해서는 '우리은행' 검색어가 유의미하게 줄거나 늘었을 때 '국민은행' 검색어가 어떻게 변했는지를 확인해야 한다.

5. 상관계수의 범위 증명

두 확률변수 $X$, $Y$에 대한 상관계수 $\rho=Corr(X,Y)$ 의 범위는 [-1, 1]로 알려져 있다. 증명해 보자.
먼저 확률변수 $X$, $Y$ 외에 다음의 두 확률변수 $U$, $V$를 다음과 같이 정의하면,

$U=\frac{X-E(X)}{\sigma_X}, V=\frac{Y-E(Y)}{\sigma_Y}$

이들의 $E(U)=E(V)=0, \sigma_U = \sigma_V = 1$ 이 된다. (참고로 $\sigma_U=\frac{1}{\sigma_X^{2}}Var(X-E(X)) =\frac{Var(X)}{\sigma_X^{2}} = \frac{\sigma_X^{2}}{\sigma_X^{2}}=1$ 이다.) 이 때,

1) $Corr(U, V)=E[(U-E(U))(V-E(V))]=E(UV)-E(U)E(V) = E(UV) = E(\frac{(X-E(X))(Y-E(Y))}{\sigma_X\sigma_Y}) = \frac{Cov(X,Y)}{\sigma_X\sigma_Y} = Corr(X,Y)$ 이다.

즉, $Corr(U, V) = Corr(X, Y)$ 이다.

다음으로 $\sigma_U = \sigma_V = 1$ 을 이용한다.

2) $Var(U+V) = Var(U) + Var(V) + 2Cov(U, V) = 2 + 2\sigma_U \sigma_V Corr(U, V) = 2+2Corr(X, Y)$

$Var(U, V)$ 가 0이상이므로, $0 \le Var(U+V) = 2 + 2 Corr(X, Y)$ 이다.
따라서, $-1 \le Corr(X, Y)$이다.

3) $Var(U-V) = Var(U) + Var(V) - 2Cov(U, V) = 2 - 2\sigma_U \sigma_V Corr(U, V) = 2-2Corr(X, Y)$

$Var(U, V)$ 가 0이상이므로, $0 \le Var(U-V) = 2 - 2 Corr(X, Y)$ 이다.
따라서, $Corr(X, Y) \le +1$이다.

위의 2), 3)에 의해 $-1 \le Corr(X, Y) \le +1$ 이다.