[알고리즘] Dijkstra's Algorithm

SeongWon Oh·2021년 9월 20일

Dijkstra Algorithm dynamic programming 알고리즘 최단경로 알고리즘

알고리즘

목록 보기

10/12

최단경로 알고리즘

최단 경로 알고리즘이란 두개의 Node를 잇는 가장 짦은 경로를 찾는 알고리즘이다.
가중치 그래프와 간선의 가중치의 합이 최소가 되도록 하는 경로를 찾는게 목적이다.
최단 경로 문제 종류
- 단일 출발 단일도착 문제(single-source and single-destination shortest path problem) : 출발지와 목적지가 주어지며 그 사이에서 가장 짧은 경로를 찾는 문제이다.
- 단일 출발 문제(single-source shortest path problem) : 문제에 출발지만 주어져 출발지로부터 다른 모든 노드들 사이의 최단 거리를 찾는 문제
- 전체 쌍 문제 (all-pair) : 출발지와 목적지가 주어지지 않아 모든 쌍에 대한 최단 경로를 찾는 문제
대표적인 알고리즘으로는 다익스트라 알고리즘이 있다.

다익스트라 알고리즘 (Dijkstra's Algorithm)

다익스트라 알고리즘은 대표적인 최단 경로 알고리즘으로 단일 출발 문제에 해당해 하나의 정점에서 다른 정점간의 최단 거리를 구하는 알고리즘이다.
첫 node를 기준으로 연결되어 있는 Node들을 추가해가며 최단 거리를 갱신하는 기법이다.
인공위성 GPS소프트웨어 등에서 많이 사용된다.
BFS(너비우선탐색)과 유사하다.
이전 Node까지의 최단 거리를 이용하여 문제를 풀기에 DP(Dynamic Programming)문제로 볼 수 있다.
전체적인 순서
1. 초기 node의 거리는 0, 다른 node의 거리는 무한대로 저장한다.
2. PriorityQueue에 첫 정점 정보만 넣는다.
3. PriorityQueue에서는 node를 꺼내며 해당 node(u)와 연결된 node(v)들을 탐색하며 연결된 v의 edge의 weight+u의 distance가 v의 distance보다 작다면 값을 업데이트해주고 v를 Queue에 추가해준다.
4. 3번 과정을 PriorityQueue가 빌때까지 반복한다.

다익스트라 알고리즘 구현

👨🏻‍💻 Code구현을 위해 만든 객체들

코드 구현을 위해서는 Node명과 weight정보를 갖고 있는 NodeWeight과 최종 결과를 저장할 Node의 정보와 최종 거리를 저장하는 NodeDistance객체를 만들었다. NodeDistance객체는 PriorityQueue를 통해 poll을 하기 위해 Comparable method를 재정의 하였다.

class NodeWeight {
	char node;
	int weight;
	

	public NodeWeight(char node, int weight) {
		this.node = node; 
		this.weight = weight;
	}
	
}

class NodeDistance  implements Comparable<NodeDistance>{
	char node; 
	int distance;
	
	public NodeDistance(char node, int distance) {
		this.node = node;
		this.distance = distance;
	}
	
	@Override
	public int compareTo(NodeDistance o) {
		// TODO Auto-generated method stub
		return this.distance > o.distance? 1:-1;
	}	
}

👨🏻‍💻 Full Code

package algorithm;

import java.util.*;

class NodeWeight {
	char node;
	int weight;
	

	public NodeWeight(char node, int weight) {
		this.node = node; 
		this.weight = weight;
	}
	
}

class NodeDistance  implements Comparable<NodeDistance>{
	char node; 
	int distance;
	
	public NodeDistance(char node, int distance) {
		this.node = node;
		this.distance = distance;
	}
	
	@Override
	public int compareTo(NodeDistance o) {
		// TODO Auto-generated method stub
		return this.distance > o.distance? 1:-1;
	}	
}

public class Dijkstra {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		
		// Node들의 연결점, 가중치를 갖고 있는 map
		HashMap<Character, NodeWeight[]> map = new HashMap<>();
		NodeWeight[] temp = new NodeWeight[3];
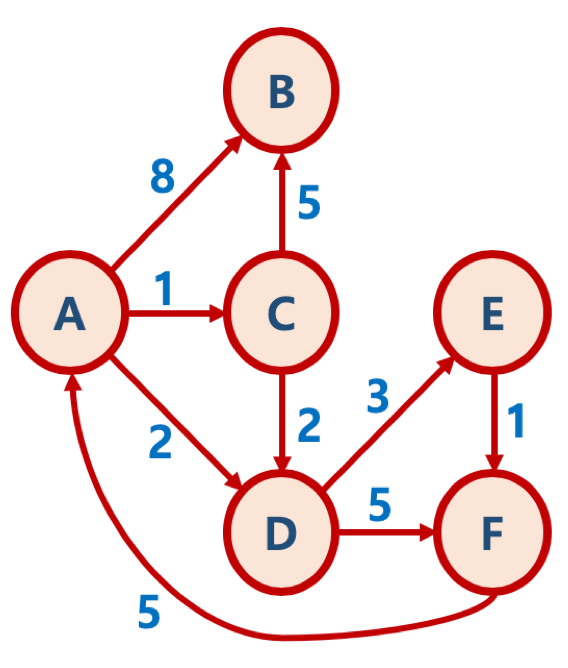
		temp[0] = new NodeWeight('B', 8);
		temp[1] = new NodeWeight('C', 1);
		temp[2] = new NodeWeight('D', 2);
		map.put('A', temp);

		temp = new NodeWeight[0];
		map.put('B', temp);
		
		temp = new NodeWeight[2];
		temp[0] = new NodeWeight('B', 5);
		temp[1] = new NodeWeight('D', 2);
		map.put('C', temp);

		temp = new NodeWeight[2];
		temp[0] = new NodeWeight('E', 3);
		temp[1] = new NodeWeight('F', 5);
		map.put('D', temp);
		
		temp = new NodeWeight[1];
		temp[0] = new NodeWeight('F', 1);
		map.put('E', temp);

		temp = new NodeWeight[1];
		temp[0] = new NodeWeight('A', 5);
		map.put('F', temp);


		HashMap<Character, NodeDistance> result = dijkstra(map, 'A');
		for (Character c: result.keySet()) {
			System.out.println(result.get(c).node + ", " + result.get(c).distance);
		}
		
	}
	
	public static HashMap<Character, NodeDistance> dijkstra(HashMap<Character, NodeWeight[]> map, char start) {
		
		HashMap<Character, NodeDistance> distance = new HashMap<>();
		for (Character c : map.keySet()) {
			if (c == start) {
				distance.put(c, new NodeDistance(c, 0));
				continue;
			}
			distance.put(c, new NodeDistance(c, 1000)); // 무한대 대신 임시로 1000대임
		}
		
		PriorityQueue<NodeDistance> queue = new PriorityQueue<>();
		queue.offer(distance.get(start));
		
		while(!queue.isEmpty()) {
			NodeDistance currentNode = queue.poll();
			//System.out.println(currentNode.node + ", "+ currentNode.distance);
			
			if (currentNode.distance > distance.get(currentNode.node).distance)
				continue;
			
			for (NodeWeight n: map.get(currentNode.node)) {
			
				int newDistance = currentNode.distance + n.weight;
				
				// 현재 위치한 node+ 현재 node로 부터 연결된 node의 weight이 현재 연결된 node에 저장된 거리보다 작으면 값 변경
				if(newDistance < distance.get(n.node).distance) {
					distance.put(n.node, new NodeDistance(n.node, newDistance));
					queue.offer(new NodeDistance(n.node, newDistance));
				}
			}			
		}
		return distance;
	}

}

시간 복잡도

다익스트라는 1. 각 Node마다 인접한 Edge를 모두 검사하는 과정과 2. 우선순위 큐에 Node/distance정보를 넣고 삭제하는 과정을 거친다.

각 Node마다 인접한 Edge를 모두 검사하는 과정의 경우는 모든 Edge를 검사하는데 O(E)의 시간이 걸린다.
모든 Edge들을 검사하며 탐색을 하고 distance가 더 적어 업데이트가 된다면 PriorityQueue에 해당 Node정보가 추가될 것이다. 이때 추가는 최악의 경우 Edge마다 한번씩 일어날 수 있어 O(E)시간이 걸리며 O(E) 개의 노드/거리 정보에 대해 우선순위 큐를 유지하는 작업은 𝑂(𝑙𝑜𝑔𝐸)가 걸린다.

그래서 총 O(E) + O(ElogE) = O(E + ElogE) = O(ElogE) 의 시간 복잡도가 걸린다.