[DCAI] 3. Class Imbalance, Outliers, and Distribution Shift

Seonuk Kim·2024년 9월 18일
Data-Centric AIkorean

Introduction to Data-Centric AI (MIT Lecture)

목록 보기
3/10
post-thumbnail

Class Imbalance: 클래스 불균형

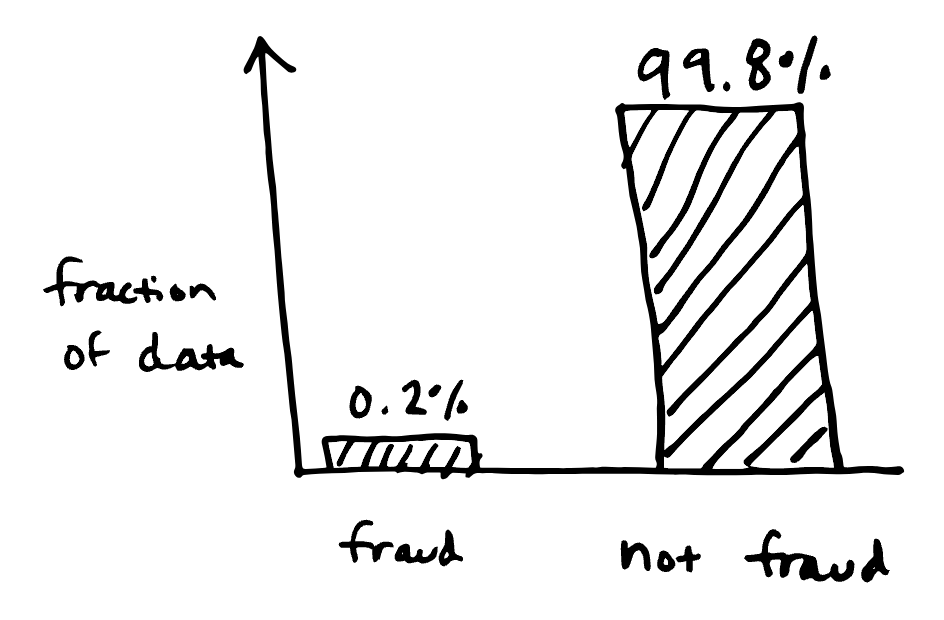
많은 실제 분류 문제에서 특정 클래스가 다른 클래스보다 더 많이 나타나는 특성이 있다. 예를 들면:

평가 지표

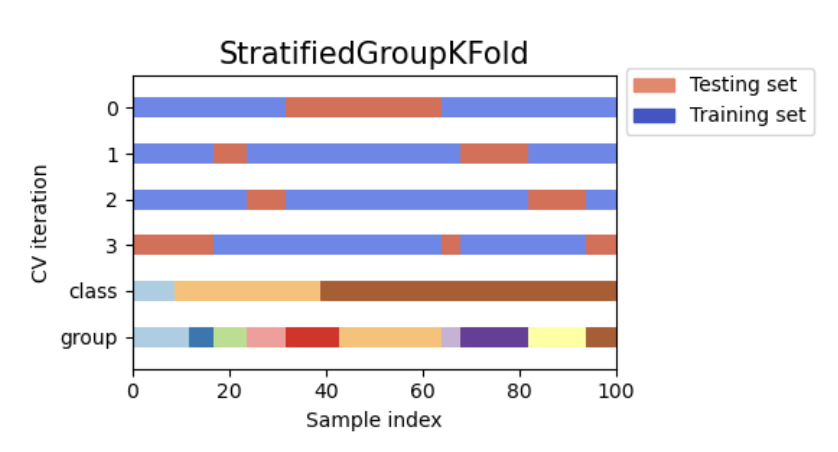
위 이미지는 Stratified Group K-Fold Cross Validation의 예시로, 데이터 분포와 비율을 실제 데이터와 유사하게 맞추는 데이터 분할 방식이다

데이터셋을 훈련/테스트 세트로 나눌 때는 stratified data splitting을 사용하는 것이 좋다. 이를 통해 훈련 분포가 테스트 분포와 일치하도록 해야 한다. 그렇지 않으면 distribution shift(분포 변화) 문제가 발생할 수 있다.

불균형 데이터(imbalanced data)에서 정확도(accuracy)와 같은 일반적인 지표는 유용하지 않을 수 있다. 예를 들어, 신용 카드 사기 탐지에서 사기 비율이 0.2%라면, 모델이 모든 거래를 “사기 아님”으로 예측할 때 99.8%의 높은 정확도를 달성할 수 있다. 하지만 이런 경우, 정확도는 중요한 평가 지표가 되지 않는다. 이상치(사기)를 정확하게 탐지하는 것이 더 중요하기 때문이다.
→ 물론 사회과학에서 같은 논리로 확률 대응(probability matching)적 접근이 중요할 때가 있다. 정확도를 높이기 위해 일부 오류를 일부로 용인하는 의사결정 기법을 의미한다. 하지만, 이 경우에는 성립하지 않는다. 자세한 내용은 심리학의 오해(How to Think Straight about Psychology) 참고

평가 지표를 선택하는 데는 정답이 없다. 문제의 특성에 맞는 지표를 선택해야 한다. 예를 들어, 신용 카드 사기 탐지 문제에서는 정밀도(precision)와 재현율(recall)의 가중 평균인 F-beta score가 적합할 수 있다. 이때 가중치는 사기 거래를 차단하지 못하는 것과 정상 거래를 잘못 차단하는 것의 비용을 고려해 결정된다.

Fβ=(1+β2)⋅precision⋅recallβ2⋅precision+recallF_\beta = \left(1 + \beta^2 \right) \cdot \frac{\text{precision} \cdot \text{recall}}{\beta^2 \cdot \text{precision} + \text{recall}}

F-beta score는 특히 재현율을 더 중요하게 생각하는 경우(즉, 사기 탐지 실패를 최소화하는 것이 중요한 경우)에 유용하게 사용된다.

불균형 데이터(imbalanced data)로 모델 훈련

평가 지표를 선택한 후, 기본적인 방법으로 모델을 훈련할 수 있다. 그러나 성능이 부족할 경우, 소수 클래스에서 성능을 개선하기 위해 아래 방법들을 활용할 수 있다.

  • 샘플 가중치 (Sample Weights): 각 샘플에 가중치를 부여해 손실의 가중 평균을 최적화하는 방법이다. 그러나 미니배치 학습에서는 미니배치 간에 효과적인 학습률이 달라져 학습이 불안정해질 수 있다
  • 오버샘플링 (Over-sampling): 소수 클래스 데이터를 복제해 데이터셋을 균형 있게 만드는 방법이다. 하지만 과적합(overfitting) 위험이 있어 주의가 필요하다
  • 언더샘플링 (Under-sampling): 다수 클래스의 데이터를 일부 제거해 균형을 맞추는 방법이다. 데이터 손실이 발생할 수 있지만, 성능 개선이 가능한 경우도 많다
  • SMOTE (Synthetic Minority Oversampling Technique): 기존 데이터를 복제하는 오버샘플링 대신, 소수 클래스의 새로운 예제를 생성하기 위해 소수 예제를 결합하거나 변형하는 데이터 증강(data augmentation)을 사용하여 데이터를 생성하는 방법이다. 특정 데이터 유형에서 효과적일 수 있으나, 이미지 데이터 같은 경우엔 적용이 어려울 수 있다. 예를 들어, 개 사진의 픽셀을 평균화해 새로운 개 사진을 만드는 것은 적절하지 않다
  • Balanced mini-batch training: 미니배치를 구성할 때 소수 클래스 데이터를 높은 확률로 포함시켜 미니배치가 균형 있게 유지되도록 한다. 데이터를 버리지 않고도 불균형 문제를 해결할 수 있는 좋은 방법이다.

위의 방법들은 조합하여 사용할 수 있다. 예를 들어, SMOTE 저자들은 SMOTE와 언더샘플링을 함께 적용하면 단순 언더샘플링보다 더 나은 성능을 기대할 수 있다고 언급하기도 했다

참고문헌

Outliers: 이상치

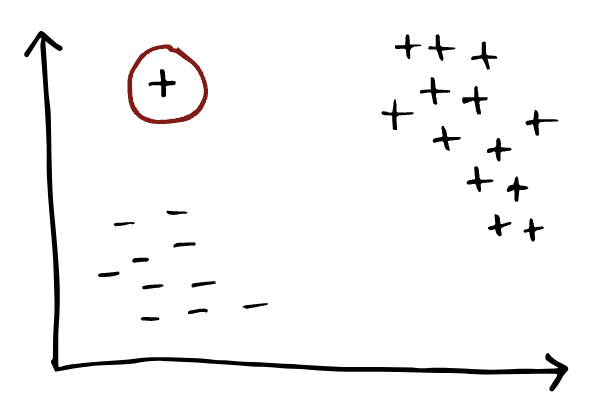
이상치의 예시. 2차원 공간에서 "+"와 "-"로 라벨링이 되어있다. 빨간색 원으로 표시된 "+"만 동떨어진 위치에서 이상치로 표시되어 있다

이상치는 다른 데이터 포인트와 크게 다른 데이터 포인트를 말한다. 발생 원인으로는 측정 오류(예: 손상된 공기질 센서), 잘못된 데이터 수집(예: 표 형식 데이터셋에서 누락된 필드), 악의적인 입력(예: 적대적 예제(adversarial expamples)), 또는 드문 이벤트(예: 백색증 동물 이미지) 등이 있다.

이상치는 모델 훈련, 추론 시 문제를 일으킬 수 있기 때문에 중요하다. 훈련 세트에 이상치가 있으면 모델의 성능이 저하될 수 있으며, 특히 기본 SVM 같은 모델은 이상치에 민감하다. 또한, 배포 시 이상치 입력은 비합리적인 출력을 초래할 수 있다(일종의 분포 변화(distribution shift)). 따라서, 이상치를 적절히 처리하는 것이 중요하다.

문제 설정

이상치와 관련된 작업은 크게 두 가지로 나눌 수 있다:

  • 이상치 탐지(Outlier detection): 라벨이 없는 데이터셋에서, 다른 데이터 포인트와 다르게 나타나는 이상치를 탐지하는 작업이다. 주로 데이터셋을 정리할 때 사용된다
  • 이상 탐지(Anomaly detection): 라벨이 없는 새로운 데이터 포인트가 주어졌을 때, 그것이 기존 데이터셋과 동일한 분포에 속하는지 판별하는 작업이다. 주로 모델 추론 시 사용된다.

이상치 탐지 기법(Identifying outliers)

이상치 탐지를 위한 다양한 방법이 존재하며, 아래 몇 가지 주요 기술을 소개한다.

  • Tukey’s fences: 스칼라 실수 값 데이터에 대한 단순한 통계적 방법으로, 사분위수를 이용해 이상치를 탐지한다. 하위 사분위수 Q1Q_1과 상위 사분위수 Q3Q_3가 주어졌을 때, 아래 범위를 벗어나는 모든 데이터 포인트는 이상치로 간주된다.

    [Q1−k(Q3−Q1),Q3+k(Q3−Q1)][Q_1 - k(Q_3 - Q_1), Q_3 + k(Q_3 - Q_1)]

    여기서 k=1.5{k=1.5}는 John Tukey가 제안한 값이며, 일반적으로 사용된다.

  • Z-점수(Z-score): Z-점수는 데이터 포인트가 평균에서 얼마나 벗어나 있는지를 표준 편차 단위로 측정한 값이다. 1차원(one-dimensional data) 또는 저차원 데이터(low-dimensional data)에 대해, 정규 분포를 가정하고, Z-점수를 다음과 같이 계산한다:

    zi=xi−μσz_i = \frac{x_i - \mu}{\sigma}

    여기서, μ\mu는 평균, σ\sigma는 표준편차다.

    Z-점수의 크기가 큰 데이터 포인트, 즉 ∣zi∣>zthr{| z_i | > z_{\text{thr}}}인 경우 이상치로 간주한다. 일반적으로 사용되는 임계값(threshold)은 zthr=3{z_{\text{thr}} = 3}이며, 이러한 기법을 각각의 feature에도 적용할 수 있다.

  • Isolation forest: 결정 트리와 유사한 방식으로, 데이터 포인트를 분리하는 데 필요한 분할 수를 기반으로 이상치를 탐지한다. 분할 횟수가 적을수록 이상치일 가능성이 높다.

  • KNN distance: k-최근접 이웃(K-Nearest Neighbors, KNN) 방법을 사용해, 데이터 포인트가 이웃과 얼마나 가까운지를 측정한다. 데이터 포인트의 k-최근접 이웃까지의 평균 거리(코사인 거리와 같은 적절한 거리 측정 기준을 선택하여)를 점수로 사용할 수 있다. 이미지와 같은 고차원 데이터의 경우, 훈련된 모델의 임베딩을 사용해 임베딩 공간에서 KNN을 수행할 수 있다.

  • 재구성 기반 방법 (Reconstruction-based Methods): 오토인코더(autoencoder)는 데이터를 저차원으로 압축한 후 다시 복원하도록 훈련된 생성 모델이다(인코딩(encoding) 후 디코팅(decoding)). 오토인코더가 데이터 분포를 학습하면, 동일한 분포를 가진 정상 데이터(in-distribution data)는 원래 입력 데이터와 유사하게 복원되지만, 분포 밖 데이터(out-of-distribution data)는 복원 오류가 커진다. 따라서, 재구성 손실값(reconstruction loss)을 이상치 탐지의 기준으로 활용할 수 있다.

이상치 탐지 기법들은 각 데이터 포인트에 점수를 부여하고, 특정 임계값을 설정해 이상치를 분류한다. 이러한 방법의 성능은 ROC curve을 통해 평가할 수 있으며, AUROC를 통해 방법들을 비교할 수 있다.

참고문헌

Distribution shift: 분포 변화

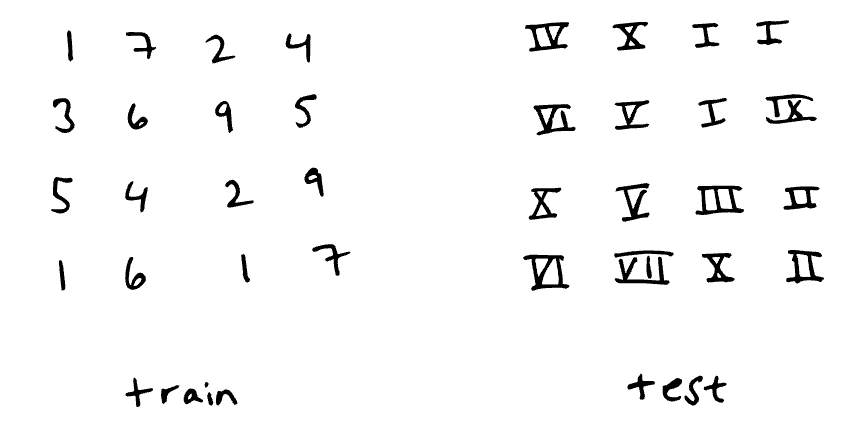
손으로 쓴 숫자 분류 작업에서의 극단적인 분포 변화(특히 공변량 변화/데이터 변화(covariate shift / data shift))의 예시. 분류기는 아라비아 숫자 0–9에 대해 훈련되었으며, 로마 숫자 0–9에 대해 평가. 이는 성능이 극도로 저하될 가능성이 있다

분포 변화(distribution shift)는 훈련 데이터와 테스트 데이터 간의 입력 및 출력 분포가 달라질 때 발생한다. 이를 수식으로 표현하면, 훈련 데이터와 테스트 데이터의 결합 분포가 다르다는 의미이다:

ptrain(x,y)≠ptest(x,y)p_\mathrm{train}(\mathbf{x}, y) \neq p_\mathrm{test}(\mathbf{x}, y)

이는 실제 머신러닝 응용에서 흔히 발생하며, 다양한 유형의 분포 변화가 존재한다.

분포 변화(distribution shift)의 유형

공변량 변화 / 데이터 변화 (Covariate shift / data shift)

공변량 변화는 입력 데이터의 분포 p(x)p(\mathbf{x})는 변경되지만, 입력과 출력 간의 관계 p(y∣x)p(y \mid \mathbf{x})는 그대로일 때 발생한다. 즉, 입력된 데이터의 분포는 훈련 데이터와 테스트 데이터 사이에서 크게 변하지만, 입력과 출력 사이의 관계는 바뀌지 않는다.

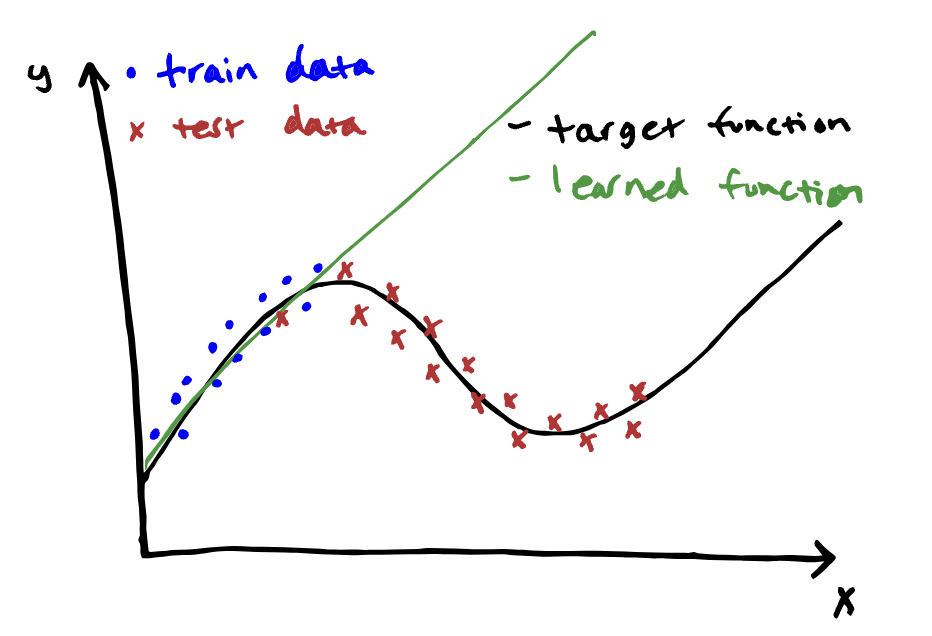
훈련 데이터와 테스트 데이터의 분포가 크게 다를 때, 학습된 모델은 훈련 데이터에 잘 맞지만 테스트 데이터에서 성능이 저하될 수 있다

공변량 변화(covariate shift)의 예시:

  • 샌프란시스코에서 훈련된 자율주행 자동차 모델을 보스턴의 눈 오는 거리에서 테스트하는 경우
  • 원어민 영어 음성을 입력으로 학습한 음성 인식 모델을 모든 영어 사용자를 대상으로 배포하는 경우
  • 보스턴 병원 데이터로 훈련된 당뇨병 예측 모델을 인도에서 배포하는 경우

개념 변화 (Concept shift)

개념 변화(concept shift)는 입력 데이터의 분포 p(x)p(\mathbf{x})는 그대로지만, 입력과 출력 간의 관계 p(y∣x)p(y \mid \mathbf{x})가 변경될 때 발생한다. 즉, 입력 분포는 동일하지만, 입력과 출력 사이의 관계가 변하는 것이다. 이는 분포 변화(distribution shift) 중에서도 가장 감지하고 수정하기 어려운 유형이다.

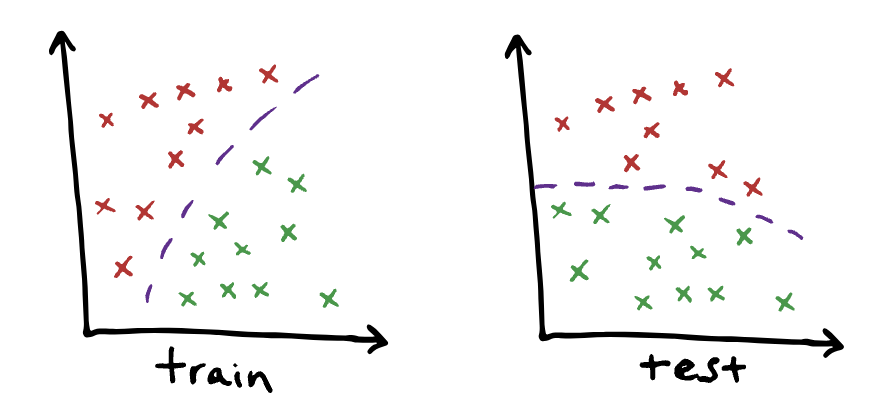
위 이미지는 2차원 특징을 가진 이진 클래스 데이터셋에서 개념 변화가 발생한 예시이다. 훈련과 테스트 사이에서 데이터 분포는 동일하지만, 클래스 간의 관계는 변경되었다

개념 변화(concept shift)의 예시:

  • 주식 예측 모델: 1975년의 회사 정보를 기반으로 주식 가격을 예측하도록 훈련된 모델이 2023년에 배포되는 경우. 주당 수익(earnings per share, EPS)(p(x){p(\mathbf{x})})은 변하지 않았지만, P/E ratio(주가 y{y}를 주당 수익 x{x}로 나눈 값)는 시간이 지남에 따라 변화되어, 동일한 수익에 대해 회사 가치는 2배 이상 더 높게 평가된다. 실제로 S&P500의 P/E ratio은 1975년에 8.30이었지만, 2023년까지 약 20으로 상승했다.
  • 구매 추천 모델: 코로나 이전 데이터를 기반으로 훈련된 구매 추천 모델이 2020년 이후의 팬데믹 기간 동안 배포되는 경우. 사용자들의 웹 브라우징 관련 행동(p(x){p(\mathbf{x})})은 변하지 않았지만(예: 대부분의 개인은 동일한 웹사이트를 브라우징하고 동일한 YouTube 동영상을 시청한다), 여행 콘텐츠와 구매 간의 관계는 크게 변했다(예: 코로나 이전에는 YouTube에서 여행 동영상을 많이 시청한 사람이 비행기 표나 호텔을 예약했을 수 있지만, 팬데믹 기간에는 자연 다큐멘터리 영화를 구입했을 수 있다)

사전 확률 변화 / 라벨 변화 (Prior probability shift / label shift)

사전 확률 변화는 출력 분포 p(y)p(y)가 훈련과 테스트 사이에서 변경되지만, 입력과 출력 간의 관계 p(x∣y)p(\mathbf{x} \mid y)는 변경되지 않는 경우 발생한다. 즉, 공변량 변화(covariate shift)와 반대되는 개념이다.

사전 확률 변화(prior probability shift)의 예시:

  • 나이브 베이즈(Naive Bayes) 기반 스팸 필터링 모델: 50% 스팸, 50% 비스팸으로 훈련된 모델이 실제로는 90%가 스팸인 이메일 환경에서 테스트되는 경우
  • 진단 예측 모델: 시간에 따라 질병 발생률이 변하는 상황에서, 질병의 발생 확률이 훈련 데이터와 테스트 데이터 간에 차이가 나는 경우

분포 변화 감지 및 처리(Detecting and addressing distribution shift)

모델 배포 시 성능 저하의 원인이 되는 분포 변화(distribution shift)를 감지하고 해결하는 방법은 다음과 같다:

  • 모델 성능 모니터링: 정확도(accuracy), 정밀도(precision)와 같은 평가 지표를 지속적으로 모니터링한다. 시간이 지남에 따라 성능 지표가 변화하면, 이는 분포 변화 때문일 수 있다.
  • 데이터 모니터링: 훈련 데이터와 배포 환경에서 수집된 데이터를 비교하여, 데이터의 통계적 특성 변화(data shift)를 감지할 수 있다.

전반적으로, 분포 변화(distribution shift)는 데이터를 수정하고 모델을 재학습시켜 해결할 수 있다. 경우에 따라 더 나은 training set를 수집하는 것이 최선일 수 있다.

공변량 변화(covariate shift) 처리

라벨이 없는 테스트 데이터가 있을 경우, 공변량 변화(covariate shift)를 처리하는 한 가지 방법은 샘플 가중치(sample weights)를 부여하는 것이다. 훈련 데이터의 각 샘플에 가중치를 적용하여, 훈련 데이터의 분포가 테스트 데이터의 분포와 유사하게 만든다.

개념 변화(concept shit) 처리

개념 변화(concept shift)는 라벨이 없는 테스트 데이터만으로는 감지하거나 해결하기 어렵다. 라벨이 없으면 개념 변화를 정량화할 방법이 없기 때문에, 이를 처리하려면 변화의 형태를 미리 알고 있어야 한다.

참고문헌

References

profile
Seonuk Kim
Content Creator and Researcher with AI technology
이전 포스트

[DCAI] 2. Label Errors and Confident Learning

다음 포스트

[DCAI] 4. Dataset Creation and Curation

0개의 댓글