데이터셋 수집 및 정제(Dataset Creation and Curation)

지도 학습을 위한 데이터셋을 생성하려면 예제와 라벨의 수집이 필요하다. 이 포스팅에서는 분류 작업(classification tasks)에 초점을 맞추지만, 이 아이디어는 회귀(regression), 이미지 세그멘테이션(image segmentation), 엔터티 인식(entity recognition) 등 다른 지도 학습 작업(supervised learning tasks)에도 적용될 수 있다. 다음 세 가지 주제를 다룬다:

1. ML 작업이 올바르게 정의되었는지에 대한 고려사항 (예: 우리가 예측하려는 클래스가 적절하게 정의되어 있는가)
2. 데이터 수집 시의 고려사항 (예: 선택 편향(selection bias))
3. 라벨 수집 시의 고려사항 (예: 여러 데이터 라벨러와 함께 작업하는 방법 및 품질 평가)

이 포스팅에서는 데이터셋 수집/정제와 인간 작업자를 통한 데이터셋 라벨링 같은 복잡한 주제 중 일부만 다룬다. 더 자세한 내용은 Human-in-the-Loop ML textbook에서 참고하길 바란다.

데이터 소싱(Sourcing Data)

훈련 데이터를 찾을 때 다음과 같은 중요한 질문을 고려해야 한다:

1. ML 모델이 어떻게 사용될 것인가? (모델이 어떤 인구집단에 대해 언제 예측을 하게 될 것인가?)
2. 모델이 정확한 예측을 해야 하는 가상의 엣지 케이스(edge cases)나 높은 위험 시나리오(high-stakes scenarios)는 무엇인가?

Beery et al. (2018)의 예를 고려해보자. 왼쪽 이미지에서는 훈련된 이미지 분류기가 소가 포함되어 있다고 올바르게 예측하지만, 오른쪽 이미지에서는 동일한 예측을 하지 못한다. 그 이유는 무엇일까?

이는 소가 훈련 데이터셋에서 항상 풀밭에서만 촬영되었기 때문일 가능성이 높다. 모델을 훈련할 때, 데이터의 특징과 라벨 사이의 다양한 상관관계를 항상 인식해야 한다. 고용량의 ML 모델은 목표를 향한 지름길을 찾는 부정행위(cheater)와 같아서, 실제 세상(real-world)에서 일반화되지 않는 허위 상관(spurious correlations)라도 데이터셋에서 높은 정확도를 내기 위해 활용하려고 한다.

선택 편향(Selection Bias)

허위 상관(spurious correlations)은 선택 편향(selection bias)으로 인해 데이터셋에 존재할 수 있다. 이는 우리가 수집한 훈련 데이터의 분포와 모델이 배포될 실제 분포 사이의 체계적인 차이를 의미한다. 즉, 우리의 데이터셋이 우리가 관심을 가져야 하는 실제 세상(real-world setting)을 대표하지 못하는 것이다. 교란(confounding)이나 분포 변화(distribution shift)라고도 불리는 선택 편향은 모델링으로 보정하기가 매우 어렵다. 따라서 데이터를 수집하기 전에 편향이 데이터에 스며들 수 있는 잠재적 이유를 항상 나열해야 한다.

선택 편향의 일반적인 원인은 다음과 같다:

• 시간/위치 편향(Time/location bias): 과거에 수집된 데이터를 미래의 데이터가 다르게 보일 응용 프로그램에 사용하거나, 한 국가에서 수집된 데이터를 전 세계에 배포되는 모델에 사용하는 경우.
• 인구통계학적 편향(Demographics bias): 특정 소수 집단이 과소 대표되는 사람들에 대한 훈련 데이터.
• 응답 편향(Response bias): 설문 조사 응답률, 질문에 대한 유도 편향 또는 선택지의 편향.
• 가용성 편향(Availability bias): 가장 대표적인 데이터보다 우연히 편리한 데이터를 사용하는 것 (예: 내 친구들만 인터뷰하는 경우).
• 롱테일 편향(Long tail bias): 다양한 드문 시나리오가 있는 응용 프로그램에서 수집 메커니즘이 데이터셋에 일부가 나타나지 않게 하는 경우 (예: 자율 주행 차량이 도로의 잘못된 쪽에서 부딪히는 경우).

수집된 데이터에서 선택 편향 다루기

데이터에 편향이 스며들도록 허용하면, 선택 편향은 모델링으로 완화하기 어렵다. 편향된 데이터로 훈련된 모델을 더 잘 평가하기 위한 한 가지 전략은 배포 시 예상되는 조건을 가장 잘 대표하는 validation set을 보유하는 것이다:

• 변화하는 환경에서 시간이 지남에 따라 데이터를 수집한 경우, 가장 최근의 데이터를 validation set으로 보유할 수 있다.
• 여러 위치에서 데이터를 수집하고 배포 시 새로운 위치를 만나게 될 경우, 일부 위치의 모든 데이터를 검증용으로 예약할 수 있다.
• 중요한 하지만 드문 이벤트(rare events)가 포함된 데이터의 경우, 검증 데이터(validation data)를 무작위로 선택할 때 이를 과대표집(over-sample)할 수 있다.
  
  

얼마나 많은 데이터를 수집해야 할까?

최소한 95%의 정확도를 달성하고 싶은 분류기를 훈련하려는 응용 프로그램을 고려해보자. 이를 달성하려면 얼마나 많은 데이터를 수집해야 할까? 또한, 추가 데이터를 수집하는 것이 얼마나 성능을 향상시킬 수 있을까?

다음과 같은 간단한 방법이 있다. 이미 크기 $n$의 일부 훈련 데이터 $D_{\text{train}}$과 별도의 고정 크기 검증 데이터셋 $D_{\text{val}}$이 있다고 가정하자. 먼저 다음과 같은 크기의 무작위 데이터 하위 집합의 그리드를 결정한다: $n_1 = 0.1 \cdot n, n_2 = 0.2 \cdot n, n_3 = 0.3 \cdot n, …, n_{10} = 1 \cdot n$. 그런 다음:

For $j = 1,\dots, 10$:
$\;\;$ For $i = 1, 2, …, T$:

• 크기 $n_j$의 데이터셋 $D_{ij}$를 원래 훈련 데이터에서 무작위로 샘플링
  (중복 없이, 분류에서는 이상적으로 클래스별로 층화 샘플링)
• $D_{ij}$에서 모델의 복사본을 훈련하고, $D_{\text{val}}$에서의 정확도 $a_{ij}$를 보고한다

이를 통해 작은 쌍의 집합 $\{(n_j, a_{ij})\}$를 생성한다. 이 집합을 사용하여, 원래 훈련 데이터 $D_{\text{train}}$보다 훨씬 큰 샘플 크기 $n' \gg n$의 데이터셋에서 훈련된 모델의 정확도 $a'$를 예측하는 것이 목표다. K-최근접 이웃(KNN)이나 선형 회귀 모델을 사용하여 이 예측을 하는 것이 왜 나쁜 아이디어일까?

이는 정확도에 대한 $n'$에서의 외삽(extrapolation)이 필요하기 때문이다. 외삽은 관련 데이터가 거의 없다는 점에서 모델 중심적인 접근이 필요하다. 여기서 우리는 경험적 관찰(empirical observation)에 의존할 수 있다. 모델의 성능은 다음과 같이 놀랍도록 예측 가능하다:

보간(내삽, interpolation)은 특정한 두 점 안쪽에 놓여있는 가능한 값을 구하려는 방법이지만 외삽(extrapolation)은 특정한 두 점 바깥에 놓여있는 값을 구하는 방법이다.

이 간단한 모델의 스칼라 파라미터 $a, b$를 관측값 $\{(n_j, 1 - a_{ij})\}$에 대한 평균 제곱 오차를 최소화하여 추정할 수 있다. 그런 다음 $n'$을 위 식에 대입하여 더 큰 크기의 데이터셋에서 훈련된 모델에 대해 예상되는 오류를 예측하면 된다.

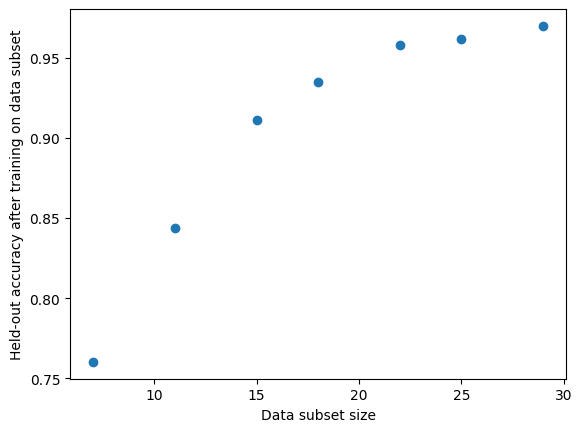
사전 정의된 검증 분할이 없는 작은 데이터셋의 경우, 교차 검증(cross-validation)을 사용하여 하위 집합에서의 $a_{ij}$ 측정을 더 안정적으로 할 수 있다.

크라우드소싱 작업자를 통한 데이터 라벨링(Labeling data with crowdsourced workers)

많은 지도 학습 데이터셋은 사람 작업자(human workers)에 의해 라벨링되어야 한다. 예를 들어, 암 종양의 의료 이미지는 의사 팀에 의해 악성(cancerous)인지 양성(benign)인지 라벨링될 수 있다. 개별 의사가 실수를 할 수 있기 때문에, 여러 의사가 독립적으로 이미지를 라벨링하면 더 신뢰할 수 있는 라벨을 얻을 수 있다.

구체적으로, 분류 데이터셋에 $n$개의 예시와 $J$명의 라벨러가 있다고 하자. 여기서 $Y_{ij} \in \{1,2,…,K\}$는 라벨러 $j$가 예시 $i$에 대해 선택한 클래스를 나타낸다. 모든 라벨러가 모든 예시를 라벨링하기는 종종 불가능하므로, 라벨러 $j$가 예시 $i$를 라벨링하지 않았다면 $Y_{ij} = \emptyset$으로 둔다. 일부 예시는 여러 라벨러에 의해 라벨링될 수 있다. 라벨링 노력을 가장 현명하게 할당하기 위해, 더 어려운 예시에 대해 더 많은 라벨을 수집하고자 한다.

이러한 방식으로 크라우드소싱 라벨을 수집할 때의 잠재적인 우려사항은 무엇일까?

1. 일부 라벨러는 다른 라벨러보다 덜 정확한 라벨을 제공할 수 있다.
2. 일부 라벨러는 다른 라벨러와 공모하여 선택을 복사할 수 있다 (맞든 틀리든).

이러한 문제를 진단하는 황금 표준 방법은 이미 정답을 알고 있는 데이터셋의 일부 품질 관리(quality control) 예시를 삽입하는 것이다. 각 라벨러에게 제공되는 데이터 하위 집합에는 품질 관리 예시가 포함되어야 한다.

여러 라벨러가 라벨링한 데이터셋의 정제(Curating a dataset labeled by multiple annotators)

데이터 라벨링 업무를 전문적으로 수행하는 사람을 데이터 라벨러(data labeler) 혹은 데이터 어노테이터(data annotator)라고 한다

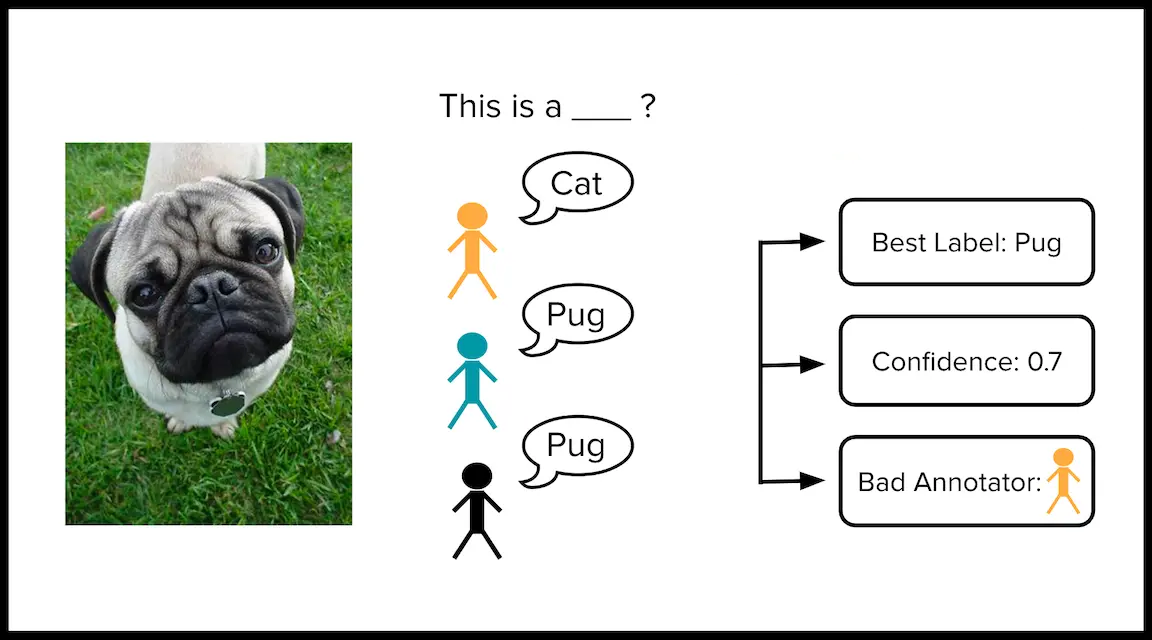
안타깝게도 여러 라벨러가 라벨링한 많은 데이터셋에는 품질 관리 예시가 포함되어 있지 않다. 이러한 데이터셋이 주어졌을 때, 다음 세 가지 양(quantities)을 추정하는 방법을 고려해 보자:

1. 개별 라벨을 종합하여 각 예시에 대한 합의된 라벨(consensus label)
2. 이 라벨이 올바르다고 확신하는 정도를 측정하는 각 합의 라벨의 품질 점수(quality score for each consensus label)
3. 각 라벨러의 전반적인 라벨 정확도를 추정하는 각 라벨러의 품질 점수(quality score for each annotator)
   
   

우리는 세 가지 알고리즘을 사용하여 위의 1-3을 추정한다:

• 다수결 투표 + 라벨러 간 합의(Majority Vote + Inter-Annotator Agreement)
• Dawid-Skene
• CROWDLAB

다수결 투표와 라벨러 간 합의(Majority Vote and Inter-Annotator Agreement)

장 간단한 방법은 예시 $i$에 대해 사용 가능한 모든 라벨(all the available annotations) $\{ Y_{ij}\}_{j \in \mathcal{J}_i}$ 중에서 다수결 투표를 통해 합의된 라벨(consensus label) $\widehat{Y}_i$를 정하는 것이다. 여기서 $\mathcal{J}_i = \{j : Y_{ij} \neq \emptyset \}$는 라벨링한 라벨러 $i$의 부분집합이다.

합의된 라벨이 맞을 가능성을, 해당 예시에 대해 각 라벨러들이 얼마나 일치하는지(agreement, 합의도)를 바탕으로 정량화할 수 있다:

라벨러 $j$의 전체적인 품질(overall quality)은, 그 라벨러가 라벨링한 예시들에서 합의된 라벨과 얼마나 일치하는지를 바탕으로 추정할 수 있다:

여기서 $\mathcal{I}_j = \{ i \in [n] : Y_{ij} \neq \emptyset \}$는 라벨러 $j$가 라벨링한 예시들의 모음(부분집합)을 나타내고, $\mathcal{I}_{j,+} = \{i \in \mathcal{I}_j : |\mathcal{J}_i| > 1 \}$는 라벨러 $j$ 외에도 다른 라벨러들이 함께 라벨링한 예시들만 포함된 부분집합이다. 즉, 라벨러 $j$의 평가를 할 때는 그 예시를 다른 라벨러도 라벨링한 경우에 한해서만 평가한다.

한계:

1. 다수결 투표에서 동점이 발생할 경우, 이를 해결하는 방법이 명확하지 않다.
2. 좋은 라벨러와 나쁜 라벨러가 동일한 가중치로 결과에 영향을 미친다.
   
   

Dawid-Skene

위의 단점을 해결하기 위해, Dawid-Skene 모델은 다수의 라벨러가 제공한 라벨 데이터를 처리하기 위해 고안된 통계적 생성 과정(statistical generative process)이다. 각 라벨러 $j$의 오류 패턴을 행렬 $\mathbf{C}_j \in \mathbb{R}^{K \times K}$로 표현하며, $\mathbf{C}_j^{a,b}$는 라벨러 $j$가 실제 클래스 $a$인 데이터를 클래스 $b$로 잘못 라벨링할 확률을 나타낸다.

이 모델은 공통 디리클레 사전 분포(joint Dirichlet prior distribution)를 적용하여, 베이지안 추론(Bayesian inference)으로 파라미터 집합 ${\mathbf{C}j}$를 추정한다. 보통 최대 사후 확률 추론(Maximum A Posteriori Probability inference, MAP inference)을 사용해 관찰된 라벨 데이터 $\{Y_{ij}\}$의 우도(likelihood)를 최대화하며, 이는 기댓값 최대화 알고리즘(Expectation-Maximization algorithm)을 통해 근사한다.

그 후, 라벨러 $j$의 품질은 $\text{Trace}(\mathbf{C}_j)$로 평가할 수 있다. 만약 $\mathbf{C}_j$가 잘 추정되었다면, Dawid-Skene의 가정에 따라 실수가 적은 라벨러일수록 $\mathbf{C}_j$의 대각선 값이 더 커야 한다.

또한, 클래스에 대한 사전 분포(prior distribution) $\pi_Y$를 가정하고(예: 데이터셋의 빈도에 비례), 예시 $i$의 실제 라벨에 대한 사후 분포(posterior distribution)는 다음과 같이 계산된다:

여기서 $\mathcal{J}_i$는 예시 $i$에 라벨을 부여한 라벨러 집합이다. 이 사후 분포는 여러 라벨러가 라벨링한 예시에 대해 하나의 클래스로 집중되며, 각 라벨러가 다른 라벨러와 일치할수록 높은 품질로 평가된다.

사후 분포에서 합의된 라벨(consensus label) $\widehat{Y}_i$는 다음과 같이 추정된다:

마지막으로, $\widehat{Y}_i$가 실제 라벨과 일치할 확신(confidence)은 $\Pr(Y_i = \widehat{Y}_i)$를 통해 계산할 수 있다.

Dawid-Skene의 한계:

1. 라벨이 예시의 특징과 어떻게 관련되어 있는지를 무시하는 강한 가정(strong assumptions)이 있다.
2. 노이즈가 있는 라벨을 제공하는 라벨러가 있을 경우, Dawid-Skene은 단일 라벨러에 의해 라벨링된 예시에 대해 신뢰할 수 있는 합의를 구축하기 어렵다.
3. Dawid-Skene는 각 라벨러마다 전체 $K \times K$ 행렬을 추정해야 하기 때문에 데이터가 적을 경우 통계적으로 어려움이 발생할 수 있다. 특히 일부 라벨러가 라벨링을 적게했거나 다른 라벨러와 많이 겹치지 않은 경우 문제가 더 심화된다.
   
   

CROWDLAB (Classifier Refinement Of croWDsourced LABels)

CROWDLAB은 예시의 특징값(feature values)을 고려하여 크라우드소싱된 라벨을 정제하는 분류 모델이다. 이 모델은 단순한 다수결 투표(majority-vote)를 통해 도출된 합의된 라벨(consensus labels)로 훈련될 수 있다.

CROWDLAB은 분류기의 확률적 예측을 라벨과 결합하여 합의된 라벨(consensus labels)과 그 품질(quality)을 추정한다. CROWDLAB의 추정치는 다음과 같은 직관에 기반한다:

• 라벨러 수에 따른 의존성: 라벨러가 적은 예시에서는 분류기의 예측에 더 많이 의존하고, 반대로 라벨러가 많은 예시에서는 덜 의존한다. 이는 많은 라벨러가 있는 경우, 단순한 합의도 높은 신뢰도를 제공하기 때문이다.
• 좋은 분류기 신뢰: 훈련된 분류기가 높은 성능을 보인다면, 라벨러 수가 적은 경우에도 분류기의 예측을 신뢰할 수 있다. 그러나 분류기의 예측이 불확실할 경우, 신뢰도를 조정한다.
• 유사한 특징값의 일반화: 좋은 분류기는 유사한 특징값을 가진 예시들에 대해 정확한 예측을 생성한다. 이러한 능력은 단일 라벨러가 라벨링한 예시의 신뢰도를 평가하는 데 도움이 된다.

CROWDLAB은 분류기의 예측 클래스 확률 $p_M = \widehat{p}_M(Y_i \mid X_i)$에 기반하여 동작한다. 이상적인 상황에서는 교차 검증을 통해 얻은 hold-out 예측을 사용한다.

특정 예시 $i$에 대해, 라벨러 $j$가 선택한 라벨 $Y_{ij}$에 대응하는 예측 클래스 확률 벡터 $p_j$를 형성한다. Dawid-Skene 모델과 마찬가지로, CROWDLAB은 이 정보를 활용하여 가중 조합(weighted combination) 방식을 통해 예시 $i$의 실제 라벨 분포를 추정한다:

여기서 $Z = w_M + \sum_{j \in \mathcal{J}_i} w_j$는 분류기와 라벨러들의 신뢰도를 반영한 가중치의 합이다. CROWDLAB은 전역 가중치 $w_M, w_1, …, w_J$를 사용하여 분류기와 라벨러의 신뢰도를 추정한다. 이 가중치는 모든 예시에 대해 동일하게 적용되며, 이를 통해 모델은 적응형 가중치(adaptive weighting) 시스템을 활용하여 신뢰도가 낮은 라벨러가 있거나 분류기가 최적이 아닌 경우에도 잘 작동한다. $\Pr(Y_i)$로부터, Dawid-Skene에서처럼 합의된 라벨(consensus label)과 그 정확성(correctness)에 대한 신뢰도(confidence score)를 계산할 수 있다.

가중치 추정 방식 (Details to estimate weights)

가중치는 라벨러 간 합의도($s_j$)와 분류기의 경험적 정확도($A_M$)를 기반으로 계산된다.

$s_j$는 라벨러 $j$가 다른 라벨러들과 얼마나 일치하는지를 나타내며, 다음과 같이 계산된다:

$A_{M}$은분류기의 다수결 합의된 라벨과의 (경험적(empirical)) 정확도(accuracy)를 나타내며, 다수의 라벨러가 라벨링한 예시에 대해 계산된다:

여기서 $Y_{i,M} \in \{1,2,…,K\}$는 모델이 주어진 입력 $X_i$에 대해 예측한 클래스를 나타낸다. 이를 기준으로 전체 데이터셋에서 가장 일반적으로 등장하는 클래스 $Y_{\text{MLC}}$의 예측 정확도 $A_{\text{MLC}}$를 구해, 기준선으로 활용한다. 이때 기준선은 여러 라벨러에 의해 라벨링된 예시들의 부분집합 $\mathcal{I}_+$에 대해서도 계산한다.

기준선을 바탕으로, CROWDLAB은 각 라벨러와 모델의 가중치를 설정한다. 라벨러 $j$의 가중치는 전체적인 합의도와 모델 정확도의 기준선에 대해 정규화된 값을 기준으로 계산된다.

라벨러의 가중치 $w_j$는 다음과 같이 계산된다:

모델의 가중치 $w_{M}$는:

예측 클래스 확률 벡터 $p_j$ 계산 (Details to estimate $p_j$)

라벨러가 직접적으로 예시 $i$에 대해 선택한 라벨 $Y_{ij}$를 사용하는 대신, CROWDLAB은 이를 예측 클래스 확률 벡터(predicted class probability vector) $p_j$로 변환한다. 이를 통해 라벨링 오류 가능성을 정량화할 수 있으며, 이는 여러 라벨러 간의 평균 합의도(average annotator agreement)를 나타내는 가능도 파라미터 $P$를 활용해 계산된다.

이때, $P$는 임의의 예시에 대해 임의의 라벨러의 라벨이 다수결로 합의된 라벨과 일치할 확률을 추정하며, 다음과 같이 정의된다:

여기서 $\mathcal{I}_{+} = \{i = 1,…,n : |\mathcal{J}_i| > 1 \}$는 여러 라벨러에 의해 라벨링된 예시를 의미한다.

최종적으로, 라벨러 $j$가 예시 $i$에 대해 선택한 라벨에 대한 예측 클래스 확률 벡터 $p_j$는 다음과 같이 간단히 정의된다:

이 방법을 통해 CROWDLAB은 라벨링 오류를 최소화하고, 데이터에서 쉽게 추정할 수 있는 단일 파라미터 $P$를 모든 라벨러가 공유함으로써 보다 일관된 예측을 할 수 있다.

라벨러 품질 추정(Estimating annotator quality)

CROWDLAB은 라벨러의 라벨링 품질과 분류기의 신뢰도를 함께 고려하여 예측의 정확성을 높인다. 라벨링 데이터의 품질을 평가하고 가중치를 조정하여 다양한 상황에서 안정적인 성능을 발휘한다.

더 자세한 내용은 CROWDLAB 논문을 참고

References

• Lecture (ver.2024): https://dcai.csail.mit.edu/2024
  • Lab: Dataset Curation with Multiple Annotators (ipynb)
• Lecture (ver.2023): https://dcai.csail.mit.edu/2023
• Lab Session (ver.2023): https://github.com/dcai-course
• P.S. 본 포스팅 작성에는 OpenAI의 GPT-4o와 o1-preview가 활용되었습니다