[DCAI] 5. Data-centric Evaluation of ML Models

Seonuk Kim·2024년 9월 18일

Data-Centric AI korean

Introduction to Data-Centric AI (MIT Lecture)

목록 보기

5/10

ML 모델의 데이터 중심 평가(Data-centric Evaluation of ML Models)

머신러닝 애플리케이션은 대체로 다음과 같은 과정으로 진행된다:

데이터를 수집하고, 해당 애플리케이션에 적합한 머신러닝 작업을 정의한다.
수집된 데이터에서 잠재적인 문제를 탐색한다.
머신러닝 모델에 적합한 형식으로 데이터를 전처리한다.
간단한 모델을 훈련시켜 성능을 검증한다.
모델과 데이터셋의 단점을 파악하고 분석한다.
데이터셋의 문제를 해결하고 이를 바탕으로 개선한다.
모델 성능을 향상시키기 위해 아키텍처 검색, 정규화, 하이퍼파라미터 튜닝 등을 수행한다.
모델을 배포한 후 성능을 지속적으로 모니터링한다.

이번 포스팅에서는 특히 5단계, 즉 모델 성능 개선의 기초가 되는 부분에 집중할 것이다. 주로 다음 주제를 다룬다:

머신러닝 모델 평가 방법 (모델 개선을 위한 전제 조건)
특정 하위 집합(subpopulations)에서의 낮은 모델 성능 처리
개별 데이터 포인트가 모델에 미치는 영향 측정

다중 클래스 분류 요약(A Recap of Multi-class Classification)

이 글에서는 분류 문제에 초점을 맞추지만, 여기서 논의되는 개념들은 다른 지도 학습 문제에도 충분히 적용될 수 있다. $K$ 개의 클래스를 가진 표준 분류 설정을 간략히 복습해보자 (Rifkin, 2008; Hastie et al., 2017)

분류 작업에서는 $n$ 개의 예제를 포함하는 훈련 데이터셋 $\mathcal{D}$ 을 사용한다: $(x_i, y_i) \sim P_{XY}$ 는 특성 $X$ 와 클래스 라벨 $Y$ 에 대한 기본 분포로부터 샘플링된 것이다. 여기서 $y_i \in {1, 2, \dots, K}$ 는 $i$ 번째 예제의 클래스 라벨(class label)을 나타내며, $x_i$ 는 해당 예제를 나타내는 특성 값이다 (예: 이미지의 픽셀 강도).

목표: 새로운 특성 값 $x$ 를 가진 예제에 대해 예측된 클래스 확률 벡터 $M(x) = [p_1,\dots, p_K]$ 을 생성하는 모델 $M$ 을 $\mathcal{D}$ 을 사용하여 훈련하는 것이다. 여기서 $k$ 번째 항목은 $P(Y = k \mid X = x)$ 를 근사한다.

특정 손실 함수(loss function)가 각 모델 예측을 평가하는 데 사용될 때, 우리는 다음을 최적화하는 모델 $M$ 을 찾는다:

\min_M \ \mathbb{E}_{(x,y) \sim P_{XY}} \ \big[ \text{Loss}\big(M(x), y \big) \big]

주요 가정(Key assumptions):

동일한 분포: 배포 중에 만나는 데이터는 훈련 데이터 $\mathcal{D}$ 와 동일한 분포 $P_{XY}$ 에서 유래한다.
독립적이고 동일한 분포 (IID): 훈련 데이터 $(x_i, y_i)$ 는 독립적이고 동일하게 분포된 (identically distributed, IID) 데이터이다.
단일 클래스: 각 예제는 정확히 하나의 클래스에 속한다.

실제로 항상 고려해야 할 사항:

두 클래스가 일부 예제에 대해 모두 적절할 수 있다고 우려될 경우 “기타” 클래스를 포함시키고 클래스를 더 명확히 구분한다 (예: “노트북”과 “컴퓨터”).
데이터의 순서가 중요한지 여부를 검토한다.

ML 모델 평가

손실 함수를 사용하여 새로운 예제 $x$ 에 대한 모델 예측과 주어진 라벨 $y$ 를 평가한다 (Zheng, 2015; Varoquaux et al., 2022). 손실 함수는 크게 두 가지 방식으로 나눌 수 있다:

예측된 클래스 $\hat{y} \in \{1,2, \dots, K\}$ 가 $x$ 에 대해 가장 가능성이 높은 클래스에 대한 평가: 모델이 가장 가능성이 높다고 예측한 클래스 $\hat{y}$ 가 실제 라벨 $y$ 와 일치하는지를 평가한다. 대표적인 지표로는 정확도(accuracy), 균형 정확도(balanced accuracy), 정밀도(precision), 재현율(recall) 등이 있다. 이는 모델의 클래스 예측이 실제 라벨과 일치하는 빈도를 측정하며, 모델 기반 의사 결정을 직접 평가한다.
각 클래스에 대한 예측 확률 $[p_1, p_2, \dots, p_K] \in \mathbb{R}^K$ 이 $x$ 에 대해 주어진 경우에 대한 평가: 대표적인 손실 함수로는 log loss, AUROC, calibration error 등이 있다. 이는 모델이 관측된 라벨 $y$ 가 각 클래스 값을 취할 확률을 얼마나 잘 추정하는지를 측정한다. 예측된 클래스 확률은 비대칭 보상 설정(asymmetric reward setting)에서 분류기 출력으로부터 최적의 결정을 내리는 데 특히 유용하다 (예: 베팅 시, 거짓 양성(false positives)이 거짓 음성(false negatives)보다 훨씬 나쁠 경우).

모델의 성능을 요약하기 위해 단일 전체 점수에 의존하는 것은 이상적이지 않지만, 일반적으로 사용된다. 대표적인 방식으로 훈련 중 보류된 예제에 대한 손실 $\text{Loss}\big(M(x_i), y_i\big)$ 의 평균을 계산하여 전체 점수를 보고하는 방법이 있다. 그러나 이 방법은 모델의 성능을 모든 면에서 평가하기에 부족할 수 있다. 대안으로 클래스별 손실을 집계하여 클래스별 정확도(per-class accuracy)나 혼동 행렬(confusion matrix)을 보고할 수 있다.

모델을 평가하는 방식은 언제나 모델을 개선하는 방식만큼 중요한 고려 사항이다. 특히 실제 애플리케이션에서는 평가 방식이 모델 성능에 큰 영향을 미친다. 예를 들어, 신용 카드 거래의 사기 vs 비사기 분류 애플리케이션 개발을 고려해야할 때, 전체 정확도를 평가 지표로 선택하는 것이 왜 문제가 될 수 있는지 알겠는가?

모델 평가 시 피해야 할 일반적인 실수는 다음과 같다:

진정으로 보류된 데이터를 사용하지 않는 것 (Kapoor et al., 2022;Open Data Science, 2019): 데이터 누수(data leakage)라고도 불리는 이 문제는 과적합(overfitting) 위험을 높인다. 모델 평가에 사용되는 데이터는 오직 평가를 위해서만 사용해야 하며, 모델의 하이퍼파라미터 튜닝이나 기타 의사 결정에 사용되어서는 안 된다. 이를 지키지 않으면 편향된 결과가 도출될 수 있다.
부정확한 라벨로 인한 문제 (Northcutt et al., 2021): 일부 데이터 라벨이 주석 오류(annotator error)로 인해 부정확할 수 있다. 예를 들어, 이미지 데이터에서 레이블이 잘못 지정된 경우, 모델이 오답을 도출해도 실제로는 올바른 예측을 한 것일 수 있다. 이를 무시하면 모델 평가에 큰 문제가 발생할 수 있다.
평균 평가 점수만으로 성능을 판단하는 것: 평균 점수는 모델의 전반적인 성능을 간단히 보여줄 수 있지만, 성능이 저조한 소수 집단을 간과하게 만들 수 있다. 이는 실질적으로 중요한 부분에서의 성능 저하를 놓치는 결과를 초래할 수 있다.

성능이 저조한 하위 집합(Underperforming Subpopulations)

성능이 저조한 하위 집합 문제는 인공지능 시스템에서 매우 중요한 이슈이다. 예를 들어, 2018년 MIT 연구에 따르면, 상업용 얼굴 인식 시스템은 밝은 피부를 가진 남성의 사진에서 오류율이 0.8%였지만, 어두운 피부를 가진 여성의 사진에서는 34.7%의 오류율을 보였다. 이런 불평등은 인공지능이 의료 애플리케이션에서도 종종 발생하며, 의료 접근성이나 진단의 정확성에 영향을 미친다 (Vokinger et al., 2021).

2018년 연구에 따르면, 상업용 얼굴 인식 서비스는 밝은 피부색 남성의 사진에서 오류율이 0.8%인 반면, 어두운 피부색 여성의 사진에서는 34.7%의 오류율을 보였다. 이러한 불평등은 의료 애플리케이션에서도 발견된다 (Vokinger et al., 2021).

이는 훈련된 모델이 특정 데이터 슬라이스에서 성능이 저조한 사례들이다. 데이터 슬라이스(data slice)는 공통된 특성을 공유하는 데이터셋의 하위 집합을 의미한다. 예를 들어, 특정 센서로 수집된 데이터, 인종, 성별, 사회경제적 지위, 나이, 위치 등 다양한 기준에 따라 슬라이스를 구분할 수 있다. 슬라이스는 데이터의 코호트(cohorts), 하위 집합(subpopulations), 또는 하위 그룹(subgroups)이라고도 불린다.

대부분의 경우, 모델 예측이 이러한 슬라이스에 영향을 받지 않도록 해야 한다. 하지만 슬라이스 정보가 명시적으로 생략되었더라도, 슬라이스 정보는 여전히 예측 변수로 사용되는 다른 특성 값들과 상관관계가 있을 수 있다. 따라서 모델을 평가할 때 슬라이스 정보를 완전히 무시하기보다는 반드시 고려해야 한다. 각 슬라이스에 대해 모델이 얼마나 잘 작동하는지를 분해하여 평가하는 간단한 방법은 해당 슬라이스에 속하는 보류된 데이터의 하위 집합에 대해 예제별 $\text{Loss}$ 의 평균을 계산하는 것이다.

다음은 특정 슬라이스에 대한 모델 성능을 향상시키는 방법들이다 (Chen et al., 2018):

더 유연한 머신러닝 모델 사용: 특정 데이터 슬라이스에서 성능을 개선하기 위해서는 더 많은 매개변수를 가진 유연한 모델을 사용하는 것이 좋다. 예를 들어, 서로 다른 하위 그룹의 특성이 겹치지 않고 라벨 간의 관계가 비선형적일 때, 비선형 모델이 두 그룹 모두를 잘 처리할 수 있다. 이와는 달리, 저용량의 선형 모델은 한 하위 그룹에서의 성능을 다른 그룹과 상쇄시켜야 하는 문제가 생길 수 있다. 이를 위한 한 바이에이션으로 원래 모델이 성능이 저조한 하위 그룹에 대해 별도의 모델을 훈련시키고 두 모델을 앙상블할 수도 있다 (Kim, 2019).

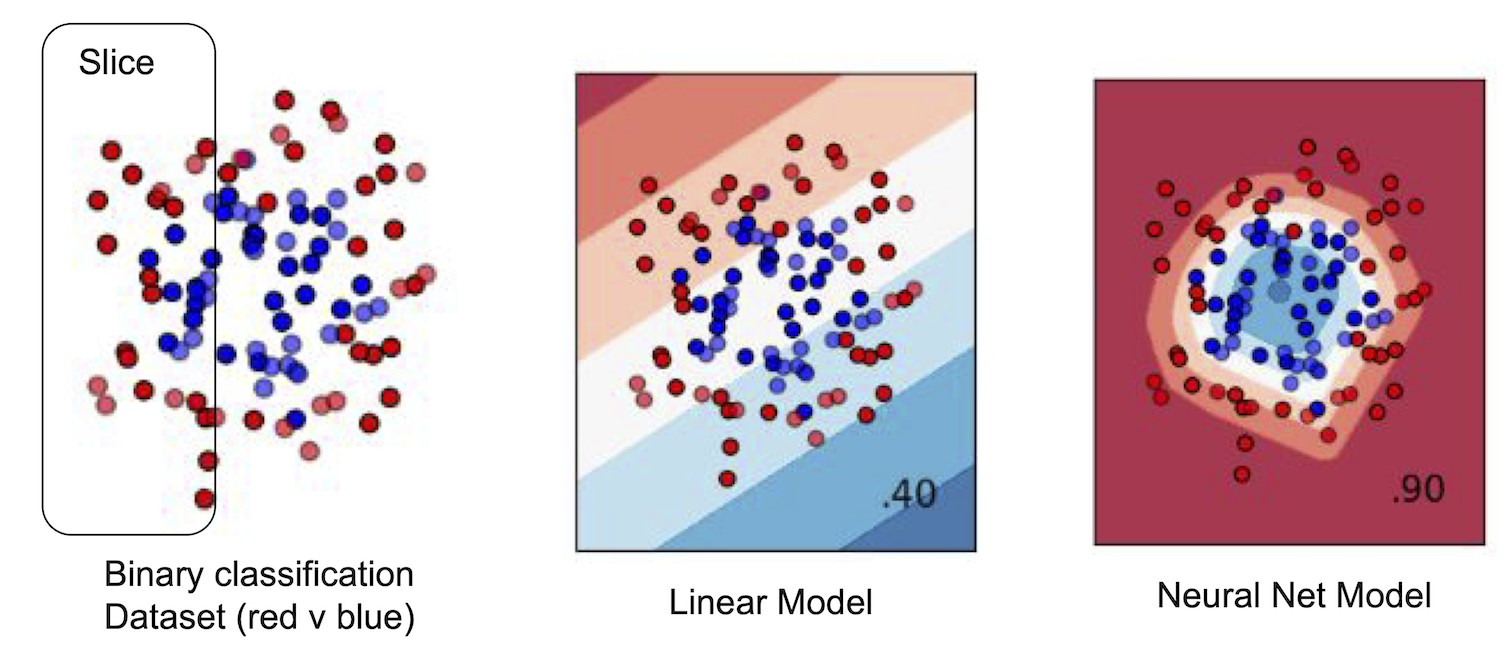
위 그림은 이진 분류 작업에서 선형 모델이 특정 슬라이스 내부와 외부의 데이터에 대해 더 나쁜 예측을 생성하는 상황을 보여준다. 더 유연한 신경망 모델은 이러한 조절 없이 슬라이스 내부와 외부 모두에 대해 정확한 예측을 생성할 수 있다.
소수 하위 그룹의 데이터 과대표집 및 가중치 부여: 성능이 저조한 하위 그룹에 속하는 데이터를 과대표집하거나 훈련 중 더 높은 가중치를 부여하는 방법도 있다. 이를 이해하기 위해, 특성 공간에서 겹치지만 라벨이 다른 경향이 있는 두 하위 그룹의 데이터를 고려해보자. 어떤 모델도 이러한 데이터를 잘 처리할 수 없으며, 분류기는 한 그룹을 잘 모델링하는 것과 다른 그룹을 잘 모델링하는 것 사이에서 상쇄를 해야 한다. 훈련 중에 특정 하위 그룹의 예제에 더 높은 가중치를 부여하면, 그 그룹에 대한 성능을 향상시킬 수 있지만 다른 그룹의 성능은 저하될 수 있다.

성능이 저조한 하위 그룹에 속하는 데이터를 과대표집하거나 훈련 중 더 높은 가중치를 부여하는 방법도 있다. 이 두 하위 그룹의 라벨이 다를 경우, 어떤 모델도 한 그룹의 예측을 더 좋게 만드는 대신 다른 그룹의 예측이 나빠지는 상쇄를 해야 한다. 오렌지 데이터 포인트에 더 높은 가중치를 부여하면, 해당 모델은 오렌지 하위 그룹에 대한 예측을 개선할 수 있지만 파란색 하위 그룹의 예측은 저하될 수 있다.
관심 있는 하위 그룹으로부터 추가 데이터 수집: 성능이 저조한 하위 그룹의 성능을 향상시키기 위한 또 다른 방법은 해당 그룹의 추가 데이터를 수집하는 것이다. 다운샘플링한 여러 대안 데이터셋에 모델을 재학습시키고 해당 하위 그룹에서 더 많은 데이터를 사용할 때 모델의 성능이 어떻게 변하는지 예측할 수 있다.
특정 하위 그룹에 대해 모델 성능을 향상시킬 추가 특성 측정 또는 설계: 원본 데이터셋의 특성들이 특정 하위 그룹의 예측을 편향시킬 수 있다. 예를 들어, 고객과 제품 특성을 기반으로 고객이 특정 제품을 구매할지 여부를 분류하는 경우, 젊은 고객에 대한 예측이 과거 관측이 적어 더 나쁠 수 있다. 이 경우, 해당 그룹에 특화된 추가 특성을 설계하여 성능을 향상시킬 수 있다. 예를 들어, 고객과 제품 특성을 사용해 구매 예측 모델을 만들 때, 젊은 고객에 대한 예측이 더 나쁜 경우 “젊은 고객 사이에서 이 제품의 인기”와 같은 추가 특성을 포함시켜 성능을 향상시킬 수 있다.

성능이 저조한 하위 집합 발견(Discovering underperforming subpopulations)

모든 데이터셋이 명확한 슬라이스(하위 집합)를 갖고 있는 것은 아니다. 예를 들어, 문서나 이미지 데이터셋에서는 슬라이스를 명확하게 정의하기 어려울 수 있다. 이 경우, 모델이 성능이 저조한 하위 그룹을 식별하는 방법은 다음과 같다:

오류 분석: 검증 데이터에서 예제들을 손실 값에 따라 정렬한 후, 손실 값이 높은 예제들을 분석하여 모델이 잘못 예측한 예제를 살펴본다. 이를 통해 모델이 자주 오류를 범하는 예제를 발견할 수 있다.
클러스터링: 손실(loss)이 높은 예제들을 클러스터링 기법으로 묶어 공통된 주제를 가진 클러스터들을 발견한다. 이를 통해 성능이 저조한 하위 집합을 식별할 수 있다. 클러스터링 기법을 사용할 때 중요한 것은 예제 간의 거리 측정 기준을 정의하는 것이며, 이를 바탕으로 성능 패턴을 분석할 수 있다.

많은 클러스터링 기법들은 두 예제 간의 거리 측정(distance metric) 기준만 정의하면 된다. 이 방법의 중요한 부분은 클러스터링 결과를 분석하여, 성능이 저조한 패턴을 발견하는 것이다. 두 번째 단계는 라벨(label)이나 손실 값(loss-value)에 의존하는 클러스터링 알고리즘을 사용할 수 있으며, 이는 Domino 슬라이스 발견 방법(Domini slice discovery method)에서 설명된다.

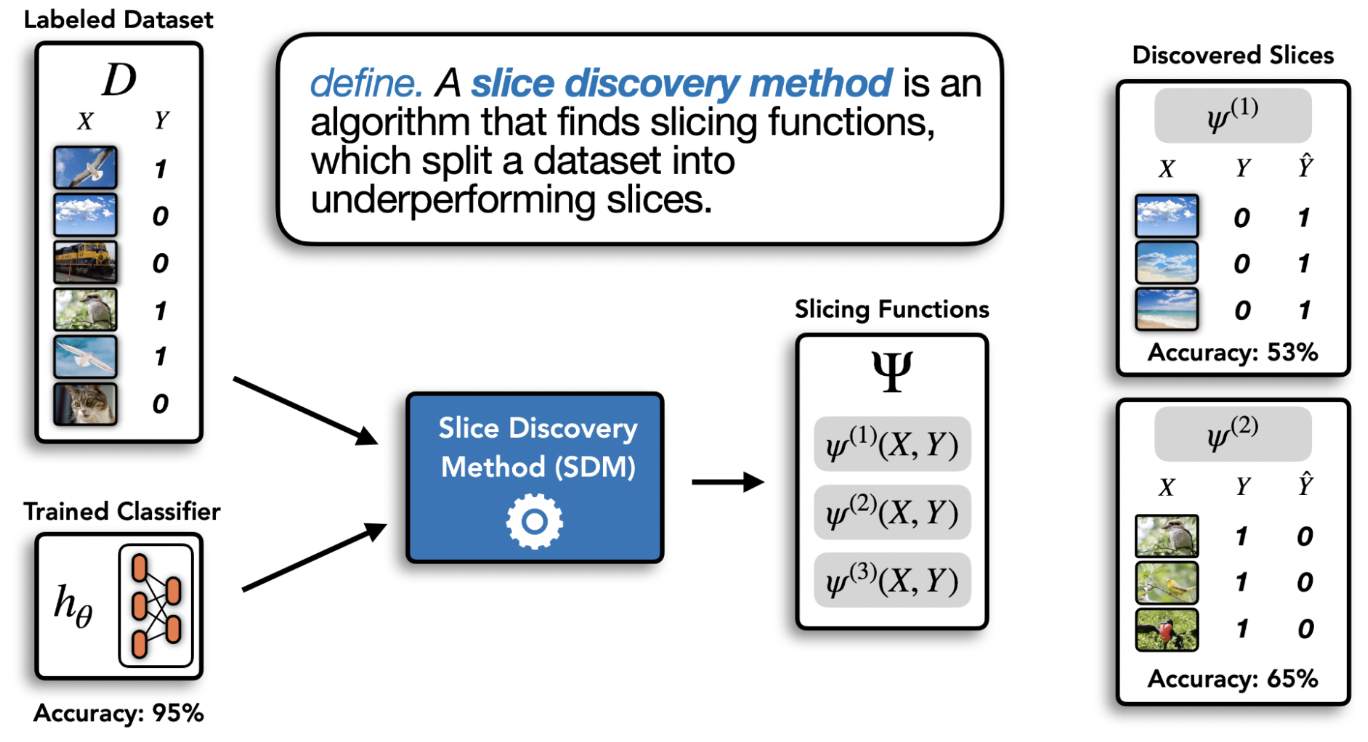
내 모델이 특정 예제를 잘못 예측한 이유는?(Why did my model get a particular prediction wrong?)

분류기가 특정 예제 $x$ 에 대해 잘못된 예측을 출력하는 이유는 다음과 같다 (Sabini, 2022):

잘못된 라벨: 예제에 붙여진 라벨 자체가 잘못되었을 수 있다. 이 경우, 모델은 사실 올바르게 예측했지만, 잘못된 라벨 때문에 오류가 발생한 것처럼 보인다.
예측 불가능한 예제: 일부 예제는 $K$ 개의 클래스 중 어느 클래스에도 속하지 않거나 예측이 어려운 경우가 있다. 예를 들어, 흐릿한 이미지나 애매한 텍스트 데이터가 여기에 해당한다.
아웃라이어: 훈련 데이터셋에 없는 예제 유형일 경우, 모델이 올바르게 예측하지 못할 수 있다. 이러한 예제는 훈련 데이터와 매우 다른 특성을 가지며, 모델이 잘 처리하지 못하는 경우가 많다.
모델의 한계: 모델이 해당 예제 유형에 대해 최적화되어 있지 않다. 이를 해결하기 위해 예제에 가중치를 높이거나 여러 번 복제하여 모델을 다시 훈련시킬 수 있다.
데이터 내 혼란: 데이터셋에 유사한 특성을 가진 예제들이 서로 다른 라벨을 가질 때, 모델은 혼란을 겪을 수 있다. 이러한 상황에서는 모델이 데이터를 일반화하는 데 어려움을 겪게 된다. 이 경우, 데이터의 가치를 풍부하게 하기 위해 추가 특성을 측정하는 것 외에는 모델 정확도를 개선할 방법이 거의 없다. 캘리브레이션(calibration) 기술을 사용하여 모델의 예측 확률을 더 신뢰할 수 있도록 조정할 수도 있다.

위의 첫 세 가지 시나리오에 해당하는 경우, 더 나은 훈련/테스트 데이터셋을 구성하기 위한 권장 조치는 다음과 같다:

잘못 주석된 예제의 라벨을 수정
데이터셋에서 라벨이 잘못된 예제가 발견되면, 가능한 한 정확한 라벨로 수정하는 것이 중요하다. 잘못된 라벨은 모델의 성능 저하로 이어질 수 있기 때문이다.
예측 불가능한 데이터 제거 또는 ‘기타’ 클래스 추가
모델이 예측할 수 없거나 $K$ 개의 클래스에 속하지 않는 예제는 제거하는 것이 좋다. 만약 이런 예제가 많다면, “기타” 클래스를 추가하는 방법도 고려할 수 있다. 이를 통해 모델의 예측 성능이 더 안정적으로 유지된다.
훈련 데이터에서 아웃라이어 제거
배포 중에 아웃라이어와 유사한 데이터가 등장할 가능성이 없다면, 훈련 데이터에서 해당 예제를 제거해야 한다. 다른 아웃라이어에 대해서는 다음과 같은 방법을 고려할 수 있다:

추가 훈련 데이터를 수집하거나,
아웃라이어의 특성을 다른 예제와 유사하게 만드는 전처리 작업을 적용하는 것
(예: 수치 특성의 분위수 정규화, 특성 삭제)

또한, 데이터 증강 기법을 사용하여 모델이 아웃라이어를 구분할 수 있도록 유도할 수 있다. 이러한 옵션이 어렵다면, 아웃라이어 데이터에 가중치를 부여하거나, 약간 변형된 여러 버전으로 데이터를 복제하여 모델이 학습할 수 있게 한다.

배포 중 아웃라이어를 적절히 탐지하려면, 머신러닝 파이프라인에 Out-of-Distribution(ODD) 탐지를 포함시키는 것이 중요하다 (Kuan et al., 2022; Tkachenko et al., 2022)

개별 데이터 포인트가 모델에 미치는 영향 측정(Quantifying the influence of individual datapoints on a model)

데이터 중심 AI에 관심이 있는 사람이라면, 특정 데이터 포인트 $(x,y)$ 를 제외한 후 모델을 재학습하면 어떻게 변화할지 궁금할 수 있다.

이 질문에 대한 답은 영향 함수 $I(x)$ 를 통해 얻을 수 있다. 영향 함수는 데이터 포인트가 모델에 미치는 영향을 정량화하는 방법으로, 여러 가지 변형이 존재한다 (Jia et al., 2021). 예를 들어, 모델의 예측 변화나 손실 변화(즉, 예측 성능의 변화)를 측정하는 방법이 있다. 여기서는 예측 성능의 변화를 중심으로 설명한다.

이러한 영향 분석 방법 중 하나는 Leave-one-out (LOO) 영향이다. 그러나 Data Shapley 값이라는 더 포괄적인 영향 분석 방법도 있다. Data Shapley 값은 데이터셋의 모든 가능한 부분 집합에서 데이터 포인트 $(x,y)$ 가 미치는 영향을 평가한다. 이 값을 모든 부분 집합에 대해 평균하면 $(x,y)$ 의 가치를 더 정확하게 평가할 수 있다 (Jia et al., 2021).

예를 들어, 동일한 데이터 포인트가 두 번 포함된 경우, 둘 다 제외했을 때 모델 정확도가 크게 떨어질 수 있다. 그러나 LOO 영향은 개별적으로 중요한지 판단할 때, 그 중요성을 과소평가할 수 있다. 반면, Data Shapley 값은 이를 더 공정하게 평가할 수 있다.

영향 함수는 모델 성능에 가장 큰 영향을 미치는 데이터 포인트를 식별하는 데 유용하다. 예를 들어, 영향이 큰 잘못된 라벨을 수정하면, 영향이 적은 라벨을 수정하는 것보다 모델의 성능 개선에 더 큰 도움이 될 수 있다. 다음 그림은 영향 함수 $I(x)$ 가 각 데이터 포인트에 가치를 할당하는 과정을 시각적으로 설명한다 (Warnesm, 2021).

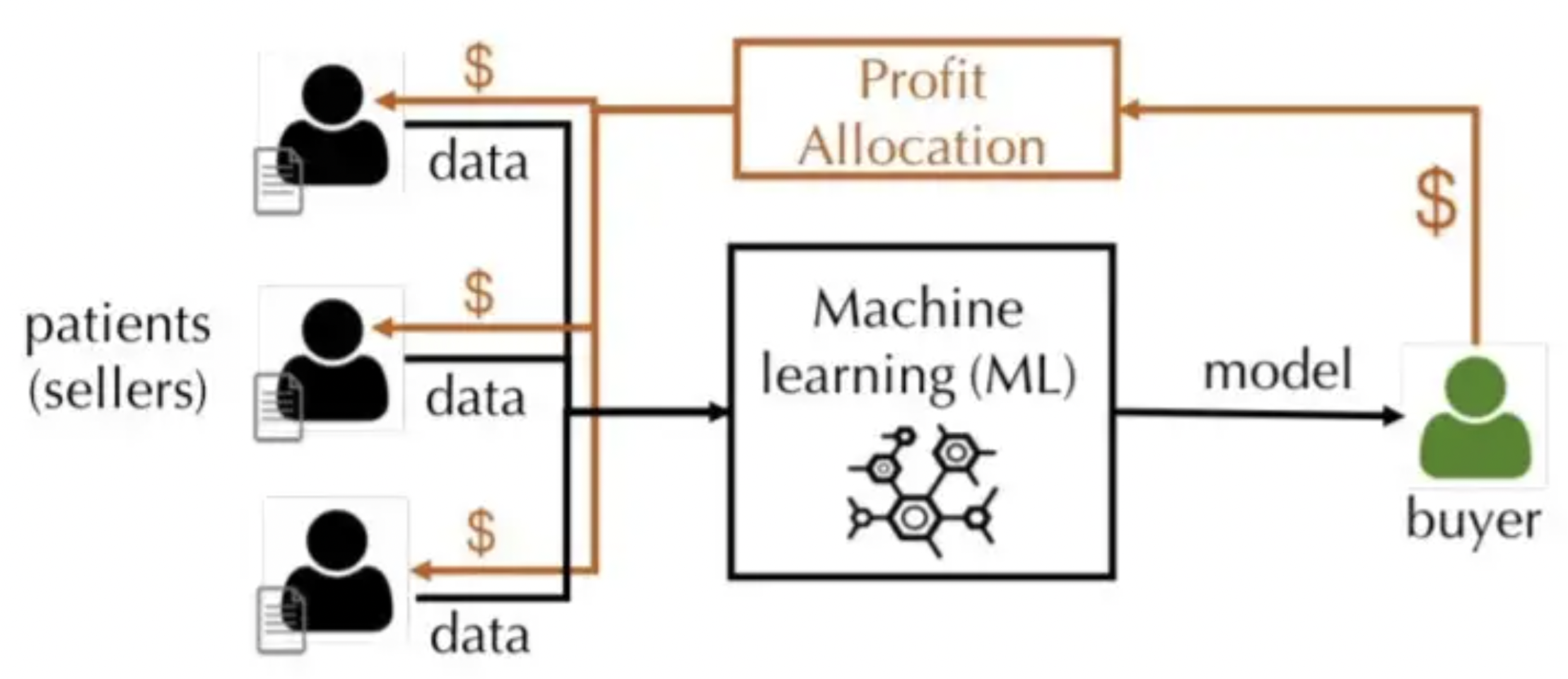
불행히도, 모든 머신러닝 모델에 대해 영향을 계산하는 것은 매우 비용이 많이 드는 작업이다. 임의의 블랙박스 분류기에 대해 다음과 같은 몬테카를로 샘플링 방법을 사용하여 영향을 근사할 수 있다::

원본 훈련 데이터셋에서 $T$ 개의 서로 다른 데이터 부분 집합 $\mathcal{D}_t$ 을 무작위로 샘플링한다 (복원 없이).
각 부분 집합 $\mathcal{D}_t$ 에 대해 모델 $M_t$ 를 학습하고, 보류된 검증 데이터에 대한 정확도 $a_t$ 를 기록한다.
데이터 포인트 $(x_i, y_i)$ 의 가치를 평가하기 위해, $(x_i, y_i)$ 가 포함된 부분 집합과 포함되지 않은 부분 집합에서 모델의 평균 정확도를 비교한다. 이를 수식으로 나타내면 다음과 같다:
$I(x_i) = \frac{1}{|D_\text{in}|} \sum_{t \in D_\text{in}} a_t \ - \ \frac{1}{|D_\text{out}|} \sum_{t \in D_\text{out}} a_t$
where $D_\text{in} = \{t : (x_i,y_i) \in \mathcal{D}_t \}$ , $D_\text{out} = \{t : (x_i,y_i) \notin \mathcal{D}_t \}$

여기서 정확도는 문제에 따라 관심 있는 다른 손실함수(loss)로 대체될 수 있다.

특정 모델군의 경우, 정확한 영향 함수를 효율적으로 계산할 수 있다. 예를 들어, 회귀 설정에서 선형 회귀 모델(linear regression model)과 평균 제곱 오차 손실(mean squared error loss)을 사용하여 예측을 평가하는 경우, 훈련된 모델의 매개변수는 데이터셋의 닫힌 형식의 함수이다. 따라서 선형 회귀에서는 Leave-one-out 영향 $I(x)$ 을 간단한 공식을 통해 계산할 수 있으며, 이 경우 쿡의 거리 (Cook’s Distance)로도 알려져 있다.

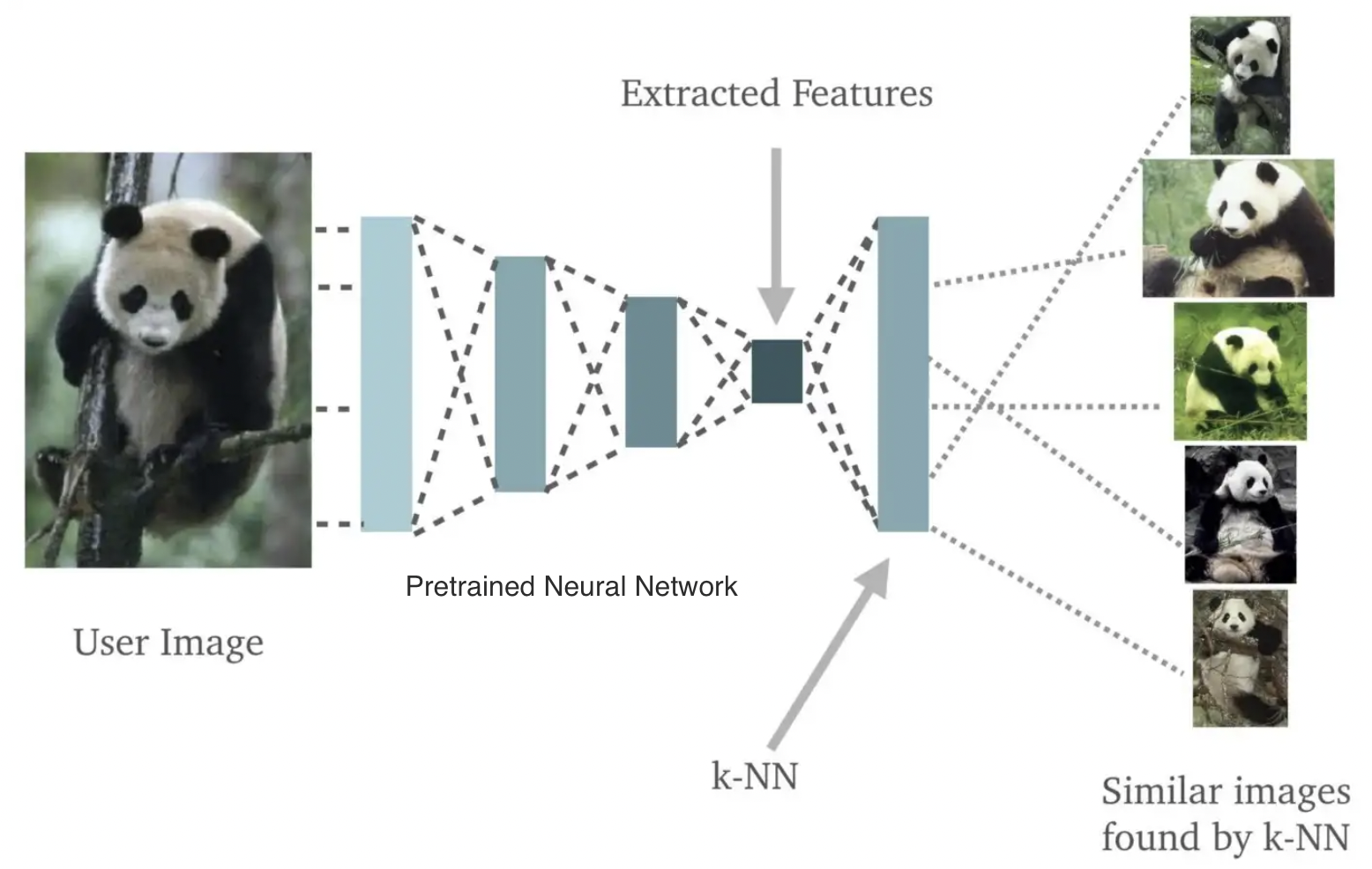
분류의 경우, K-최근접 이웃 (K Nearest Neighbors, KNN) 알고리즘을 사용하면 $O(n \log n)$ 시간 내에 영향 함수를 계산할 수 있다. 특히 비정형 데이터를 다룰 때는 사전 학습된 신경망으로 데이터를 임베딩한 뒤, 임베딩에 KNN을 적용하여 효율적으로 각 데이터 포인트의 영향을 계산할 수 있다 (Jia et al., 2021). 이 두 단계의 과정은 다음 그림에서 설명된 바와 같이 진행된다 (Kristiansen, 2018):