Structure from Motion
Structure from Motion(SfM)은 2D 이미지에서 3D 정보를 얻는 과정.
Camera Calibration
카메라 내부/외부 특징들 때문에 부정확한 3D Reconstruction이 발생할
수 있기 때문에, Calibration 진행. 영상처리, 컴퓨터비전에서도 자주 사용됨.
내부 파라미터
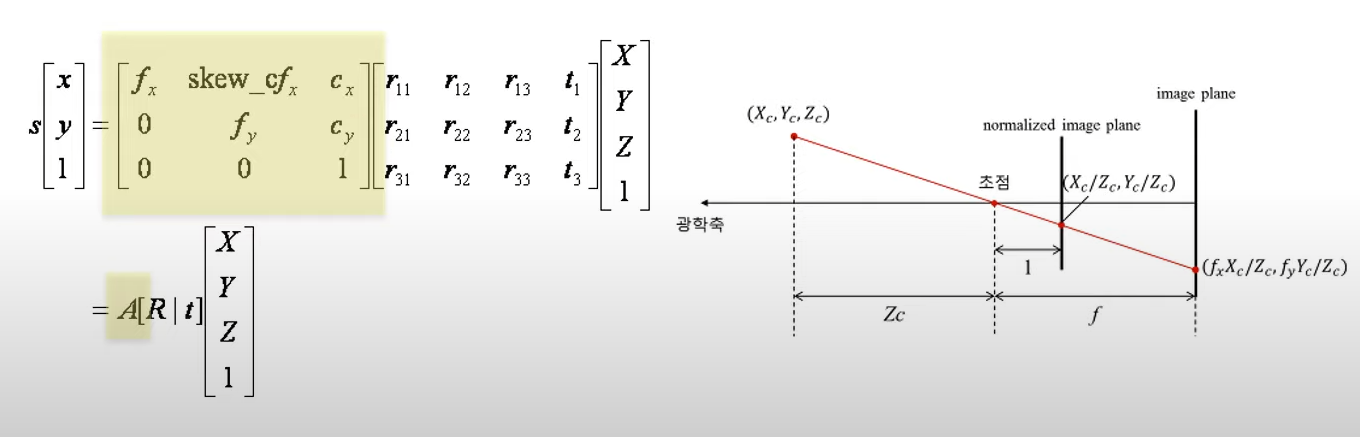
위에 보이는 matrix 연산이 Calibration임. A는 내부, R|t는 외부, XYZ는 월드 좌표계이다.
내부파라미터는 카메라 자체의 특성이다. 초점거리, 주점, 비대칭계수가 있다.
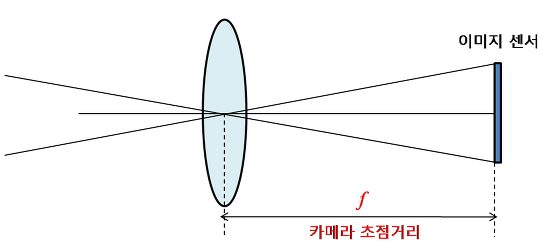
초점거리(focal length)는 렌즈 중심과 이미지 센서 사이의 거리이다. 단위는 픽셀.
(이미지 센서란 빛 정보를 전기적 정보로 바꿔주는 반도체. CCD와 CMOS가 있다.)
예를 들어 이미지 센서의 셀이 0.1mm이고, f=500pixel이면 렌즈에서 이미지 센서까지의 거리는 0.1mmX500=50mm이다.
f_x와 f_y가 존재하는 이유는 이미지 센서의 셀의 세로/가로 길이가 다를 수 있기 때문. 즉, f_x는 렌즈 중심으로부터 이미지 센서까지의 초점거리가 셀의 가로 길이의 몇배인지를 나타냄.
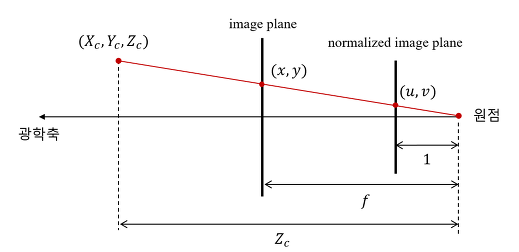
우선 XY값을 Z(초점거리)로 나누어 정규화 시킨다. 그 다음에 원하는 f(초점거리)를 곱해주면 원하는 해상도를 얻을 수 있다.
이제 c_x_c_y만 알면 된다. 주점이라 불리는 이 점은 카메라 렌즈의 중심에서 이미지 센서에 내린 수선의 발에 해당한는 위치다. 주점은 이미지의 중심과는 비슷하지만 다르다.
만약 x의 값을 원한다면 f X/Z +c_x 처럼 계산할 수 있다. c_x를 더하는 이유는 픽셀좌표가 좌상단이기 때문(bounding box 처리할 때랑 같은 논리)
다시 Calibration과정을 보자. f는 초점거리, c는 주점을 뜻한다. 행렬 연산을 해보면 f와 X가 곱해지고 c와 Z가 곱해진다. 둘을 Z로 나누면 위에서 봤던 f X/Z +c_x 이 식이 나온다.
외부 파라미터
다시 이 그림에서 가운데 있는 r이 rotation, t가 translation을 의미한다. 즉 카메라가 얼마나 돌아가있는지, 원점으로부터 얼마나 떨어져있는가를 알려준다.
Feature Detection&Description
주요 기법으로 SIFT, SURF, BRISK 등등이 있다.
오늘은 SHIT만 조사해봄.
SIFT
크기와 회전에 불변하는 특징점을 찾는 기법이다.
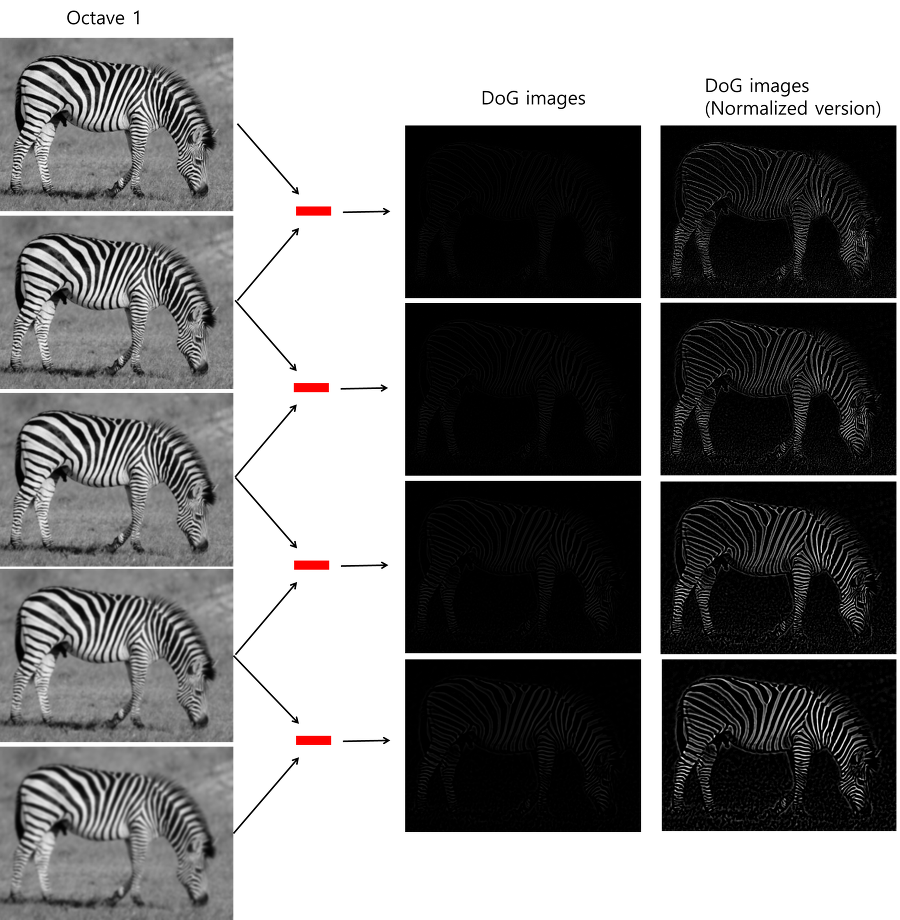
먼저 이미지를 두배 키워준 후 순차적으로 blur처리해준다. 이후 이미지 사이즈를 줄여나가며 총 20개의 이미지를 만든다.
그다음 인접한 이미지들끼리 빼준다. 자세히 보면 얼룩말의 모습이 살짝 보임. 정규화해서 더 선명하게 만든 게 오른쪽 그림. 엣지 정보를 잘 추출한다. 결과적으로 총 16장의 이미지 획득.
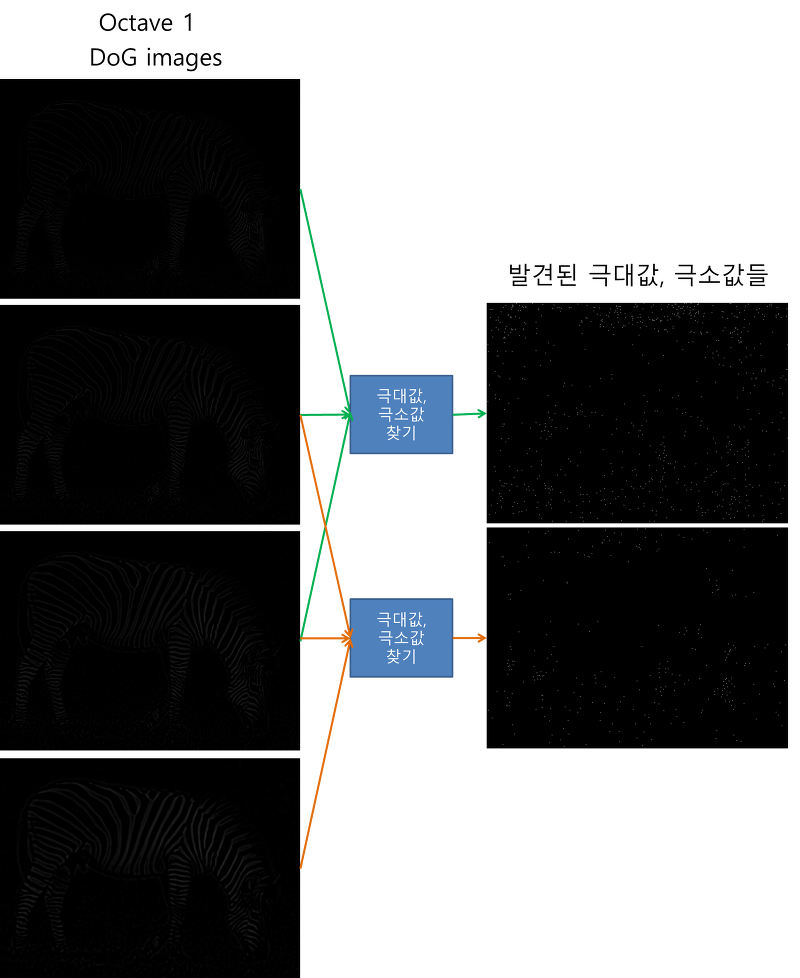
각 옥타브별로 4개씩 이미지를 획득함. 여기서 2번째 이미지 기준 위아래 이미지들과 픽셀값을들 비교.
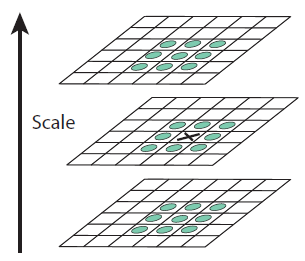
한 픽셀을 기준으로 주변 8개, 위아래 18개의 점을 비교해서 가장 큰 값을 가지거나 가장 작은 값을 가지면 이를 극대, 극소값이라고 함.
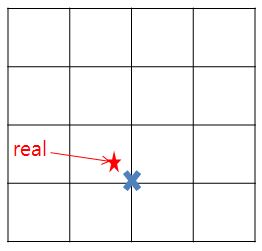
하지만 진짜 극값은 좌표 축에 존재하지 않을 가능성이 높음. 그래서 테일러 2차 전개를 사용.
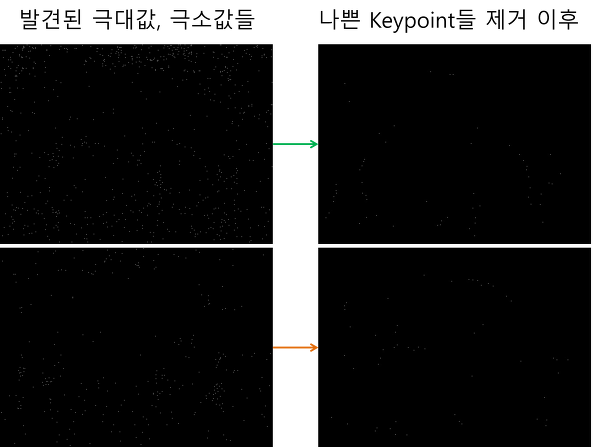
이게 0이되는 값을 찾으면 극값임. 어쨌든 그 다음으로 극값들 중 keypoint로 사용되지 못할 만한 점들을 삭제해줌. threshold로 정한 픽셀값을 넘지 못하는 경우와 엣지에 존재하는 경우를 찾아서 삭제해준다.
keypoint에서 수직, 수평 gradient를 계산해서 코너를 찾아서 남김.
최종 결과. 이제 scale invariance 만족. rotation invariance 만족시킬 차례.
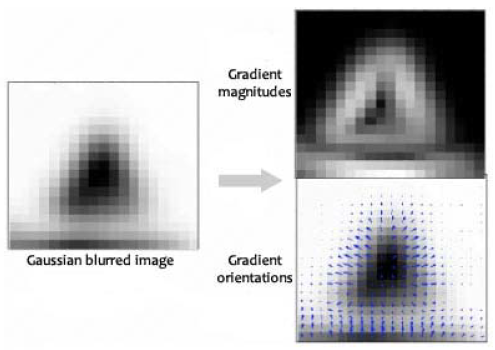
모든 점들에 대해 gradient계산.
그러고 key point에 대해 가중치 부여.
각도 별로 히스토그램을 만들어 가장 큰 값을 가지는 방향을 keypoint의 방향으로 설정함.
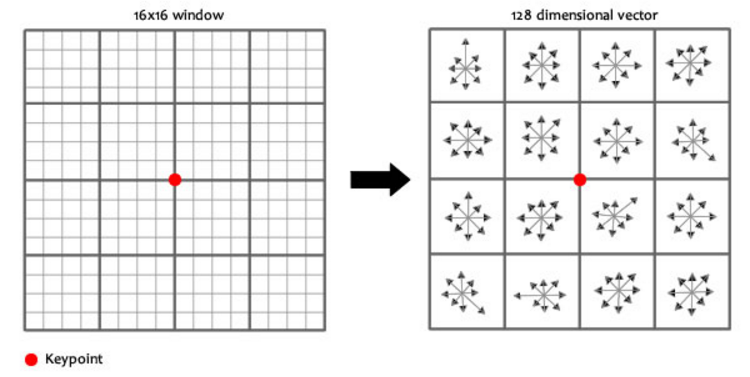
그 다음 keypoint 주변에 대한 정보를 만듦. 이를 지문(finger print)라고 부름. 이 지문의 각도에서 keypoint의 각도를 빼고(상대적인 값), 밝기 의존성을 위해 정규화를 시켜주면 모든 과정이 끝남. 이제 크기, 각도, 밝기에 따라서 invariant하므로 어떠한 상황이든 특징점을 찾고 연결시킬 수 있음.
Epipolar Geometry
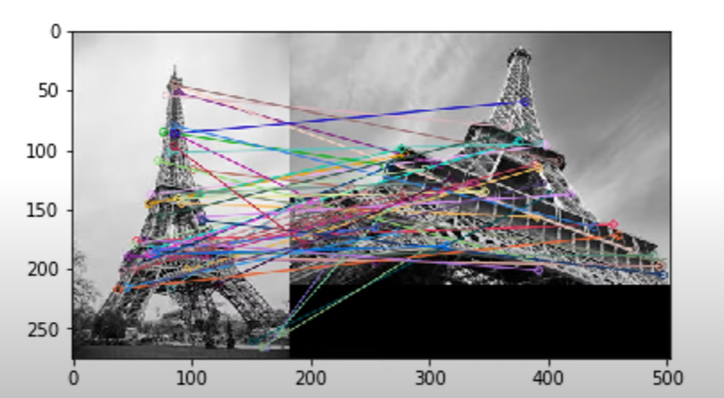
이제 서로 다른 이미지에서 특징점을 찾고 연결시킬 수 있음. 하지만 정확도를 더 높이기 위해 Epipolar Geometry 사용.
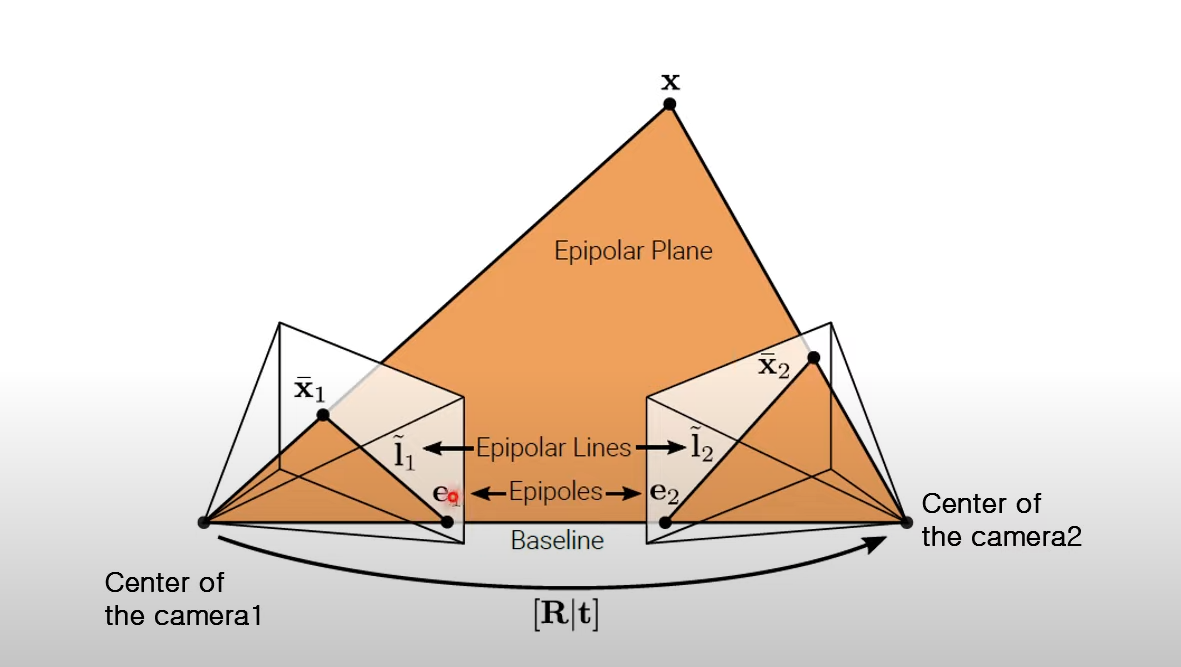
Baselilne: camera 위치를 연결한 것
Epipoles: Baseline과 Image Plane이 만나는 점
Epipolar Lines: Image Plane위의 x와 epipoles를 이은 선
이미지를 알고 카메라 위치를 알면 카메라로부터 x까지 연장선을 이을 수 있다.
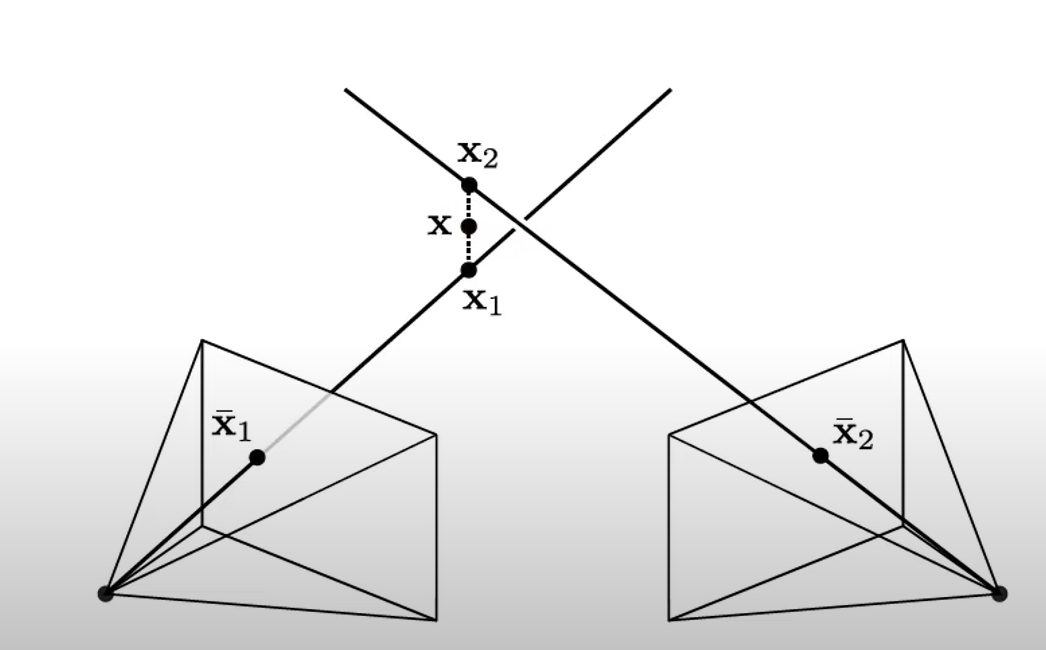
Triangulation
여전히 높이 정보는 없기 때문에 정확한 x값을 알지 못함.
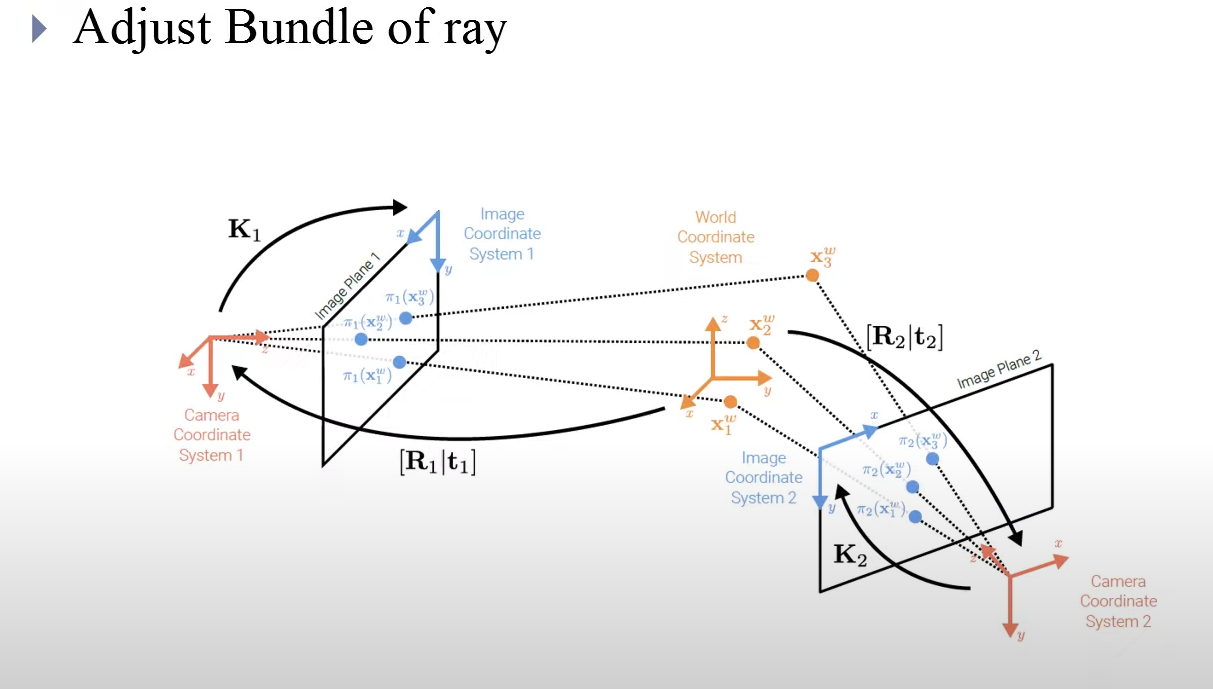
그래서 오차를 줄이는 과정이 필요함. 이거는 원래 이미지를 삼각법을 통해 실제 3D 좌표를 예상하고, 이를 다시 다른 카메라로 투영시켰을 때 크 오차를 줄이는 과정임. 근데 줄어서 결국 뭘 구하는거냐? r과 t를 구함. (외부 파라미터) 그래서 이미지들로부터 카메라의 위치를 얻을 수 있는거임.
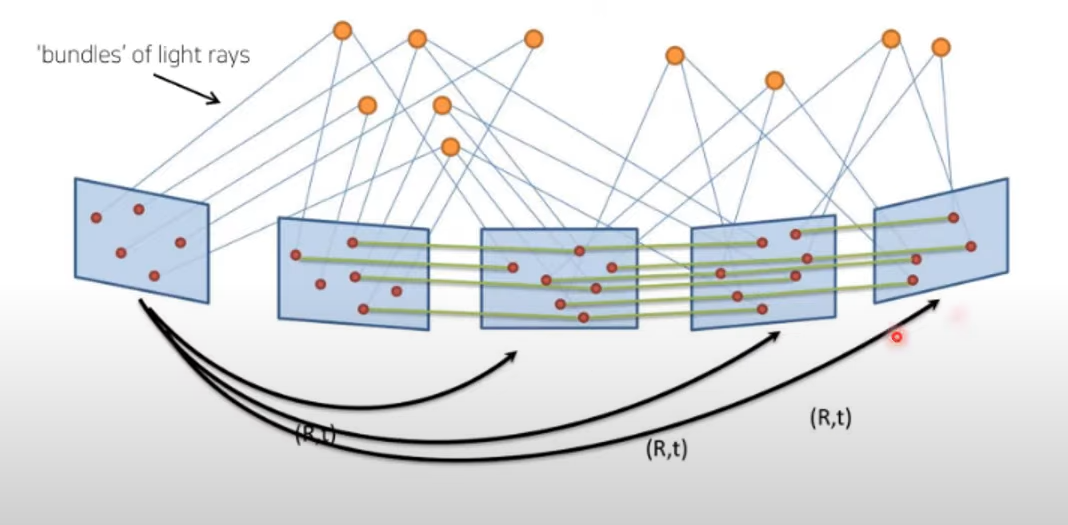
이 과정을 여러 이미지와 여러 ray에 대해 진행함.
Error 식은 위와 같음.
정리
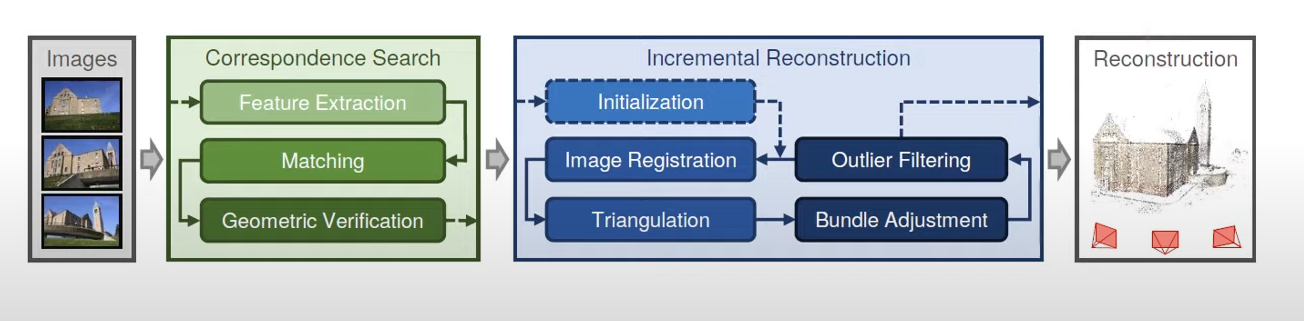
이미지 넣음. SHIT로 keypoint 찾음. keypoint 매칭시켜줌. Epipolar Geometry 좌표에 넣어줌. 삼각법을 통해 3D 좌표를 예측하고 오차를 줄이고 이상치를 제거해서 reconstruction 완성!
출처
https://www.youtube.com/watch?v=LBW7a2UkRJI
https://blog.daum.net/trts1004/12109054
https://bskyvision.com/21#:~:text=SIFT%20(Scale%2DInvariant%20Feature%20Transform,%EC%9D%84%20%EC%B6%94%EC%B6%9C%ED%95%98%EB%8A%94%20%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98%EC%9E%85%EB%8B%88%EB%8B%A4.
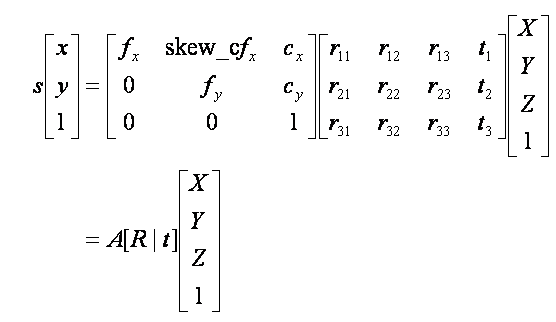

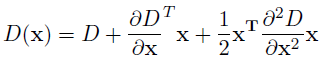

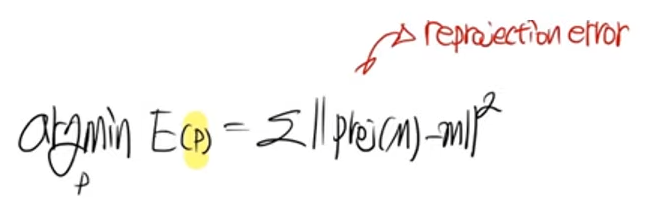

여러번 봤지만 여전히 도움이 되는 글이네요