NLP with PyTorch 03. 신경망의 기본 구성 요소

‎yeon·2023년 2월 15일

NLP with PyTorch

목록 보기

3/4

1. Perceptron: 가장 간단한 신경망

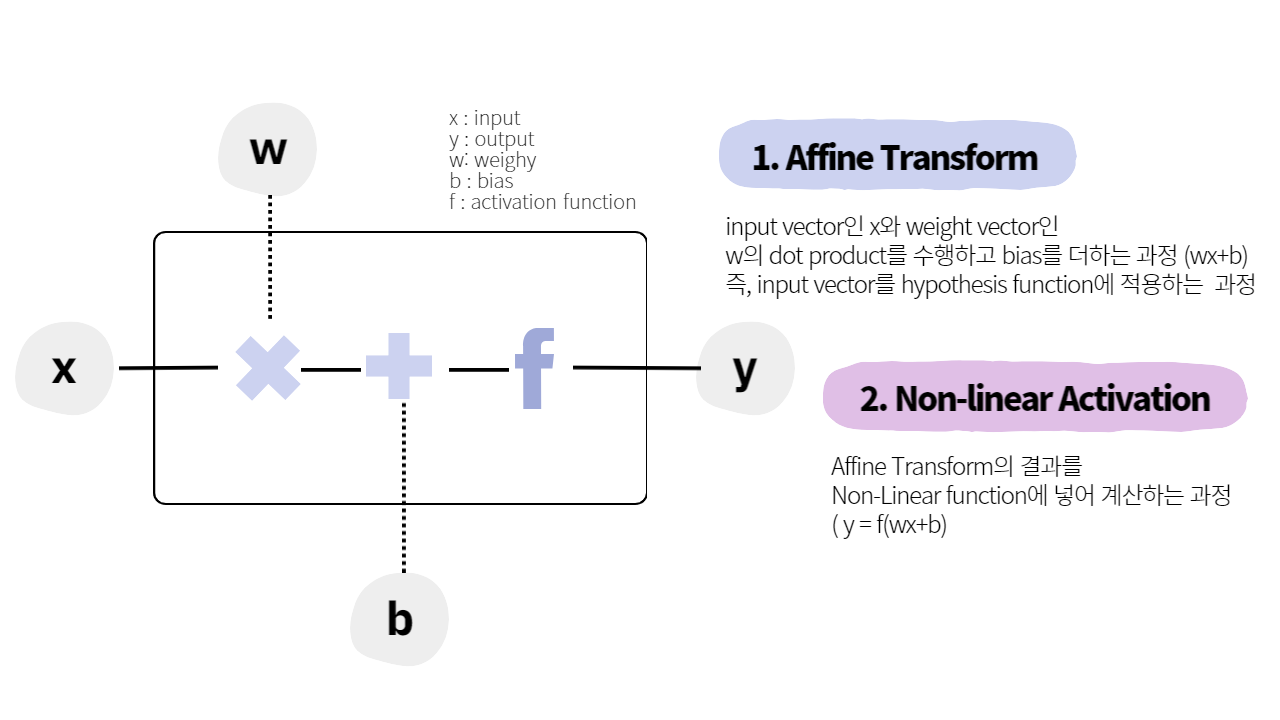
가장 간단한 신경망인 Perceptron의 유닛에는 input( $x$ ), output( $y$ )과 weight( $w$ ), bias( $b$ ), activation function( $f$ )이 있다. 해당 모델의 parameter는 weight( $w$ ), bias( $b$ )이다.

이를 식으로 나타내면 $y=f(wx+b)$ 이며 벡터 w와 x의 곱은 dot product이다.

Perceptron을 PyTorch로 구현하여 보자.

import torch
import torch.nn as nn

class Perceptron(nn.Module):
  def __init__(self, input_dim):
    super(Perceptron, self).__init__()
    self.fc1 = nn.Linear(input_dim, 1)
  
  def forward(self, x):
    return torch.sigmoid(self.fc1(x)).squeeze()

위의 코드에서 x는 input data tensor로 (batch size, number of features)의 shape을 가진다. forward(self, x)의 반환값은 perceptron의 output tensor이며 (batch, )의 shape을 가진다.

2. Activation Function

2.1 Sigmoid

Sigmoid는 임의의 실수를 받아 0과 1사이의 범위로 압축한다. 공식은 다음과 같다.
$f(x) = {1 \over {1+e^{-x}}}$
torch.sigmoid()로 구현 가능하다.

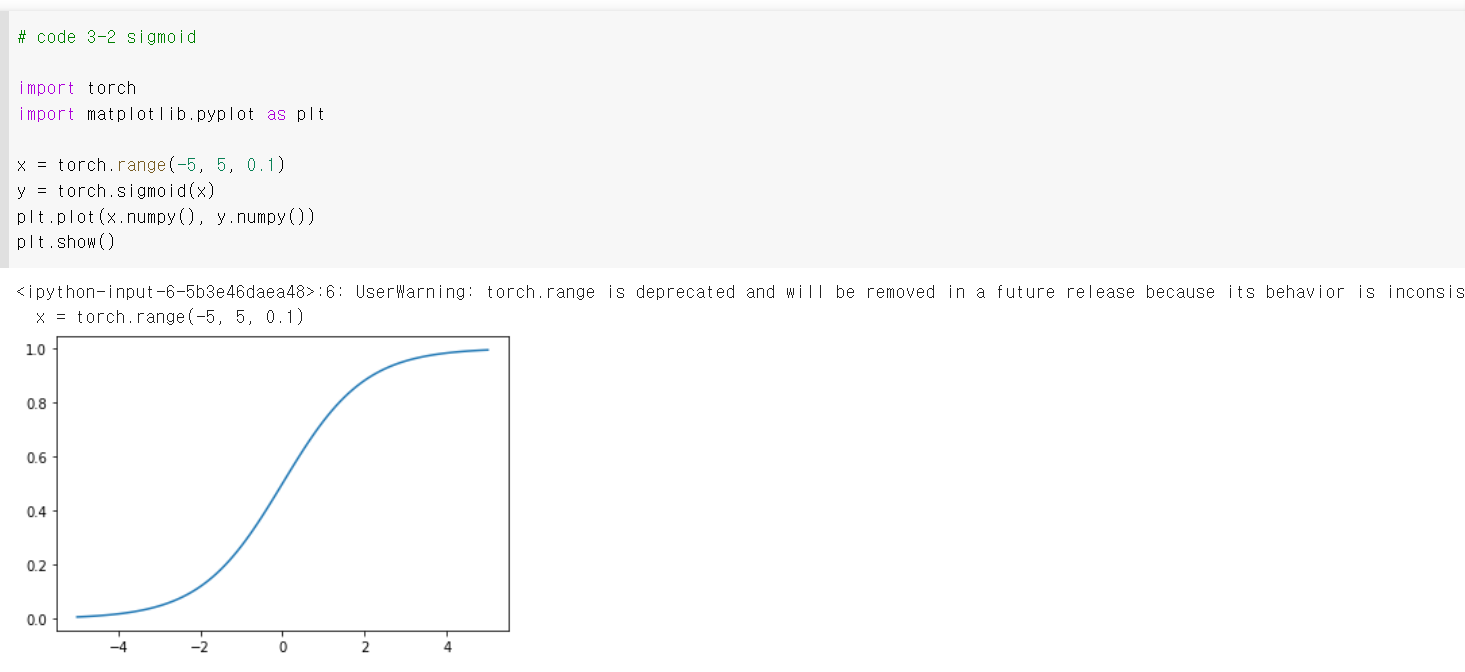
Sigmoid function은 다음과 같은 단점(drawbacks)이 존재한다.

Vanishing gradients : Sigmoid를 미분한 값, 즉 gradient가 0에 빠르게 가까워진다. Gradient가 0이 되면 update가 불가능해진다. 이러한 문제 때문에 sigmoid activation function은 거의 출력층에서만 사용한다. 출력층에서 sigmoid 사용하면 output을 0~1 사이의 확률로 표현할 수 있다.
Not zero centered : 함수값이 항상 양수이다.
Computationally expensive

2.2 Tanh (Hyperbolic tangent)

Tanh는 sigmoid의 변형으로 공식은 다음과 같다. $f(x) =$ ${e^x-e^{-x}}\over{e^x+e^{-x}}$

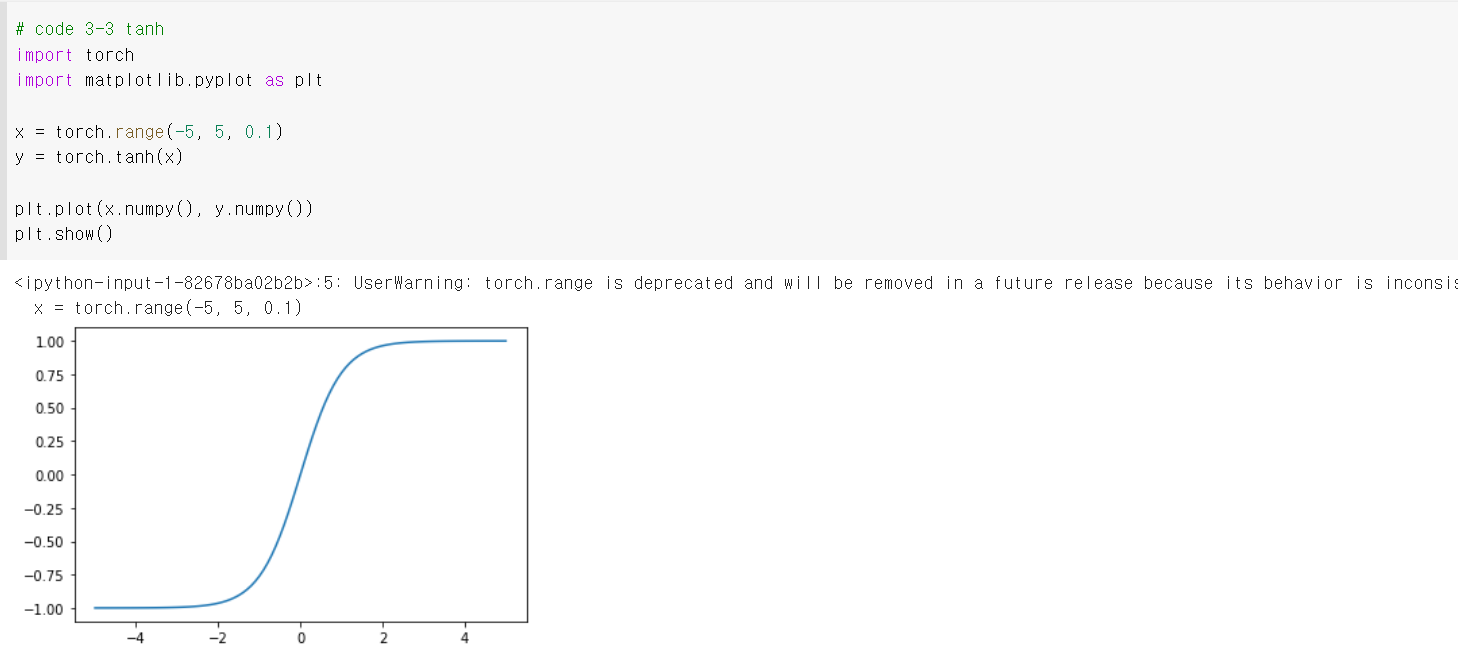
Tanh의 범위는 -1~1이며 그 중심은 (0, 0)이다(zero-centered). 하지만 여전히 vanishing gradient problem을 가지고 있다.

2.3 Rectified Linear Unit (ReLU)

ReLu의 식은 $f(x) = max(0, x)$ 이다.

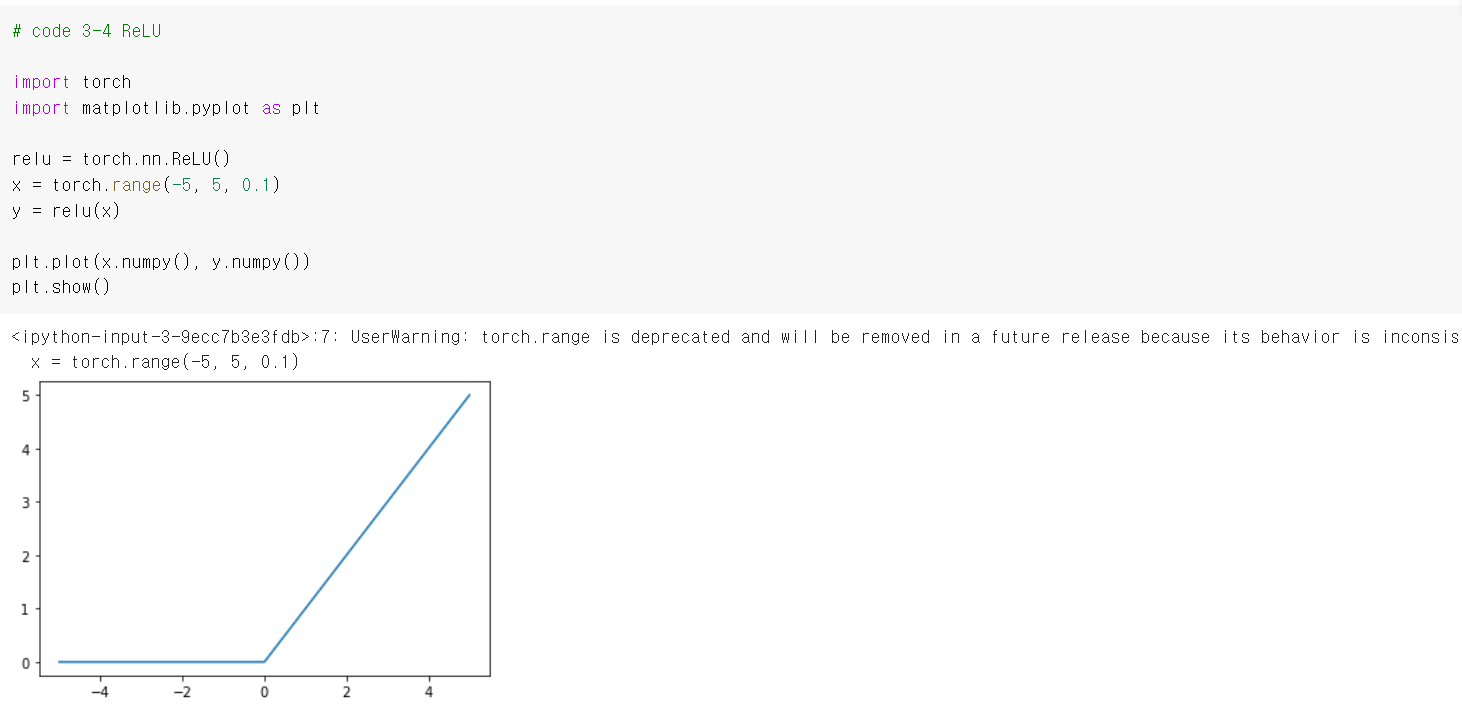
not zero-centered인 문제가 있다. 또한, $x<0$ 인 범위에서는 기울기가 0이므로 여전히 gradient vanishing 문제가 발생한다.

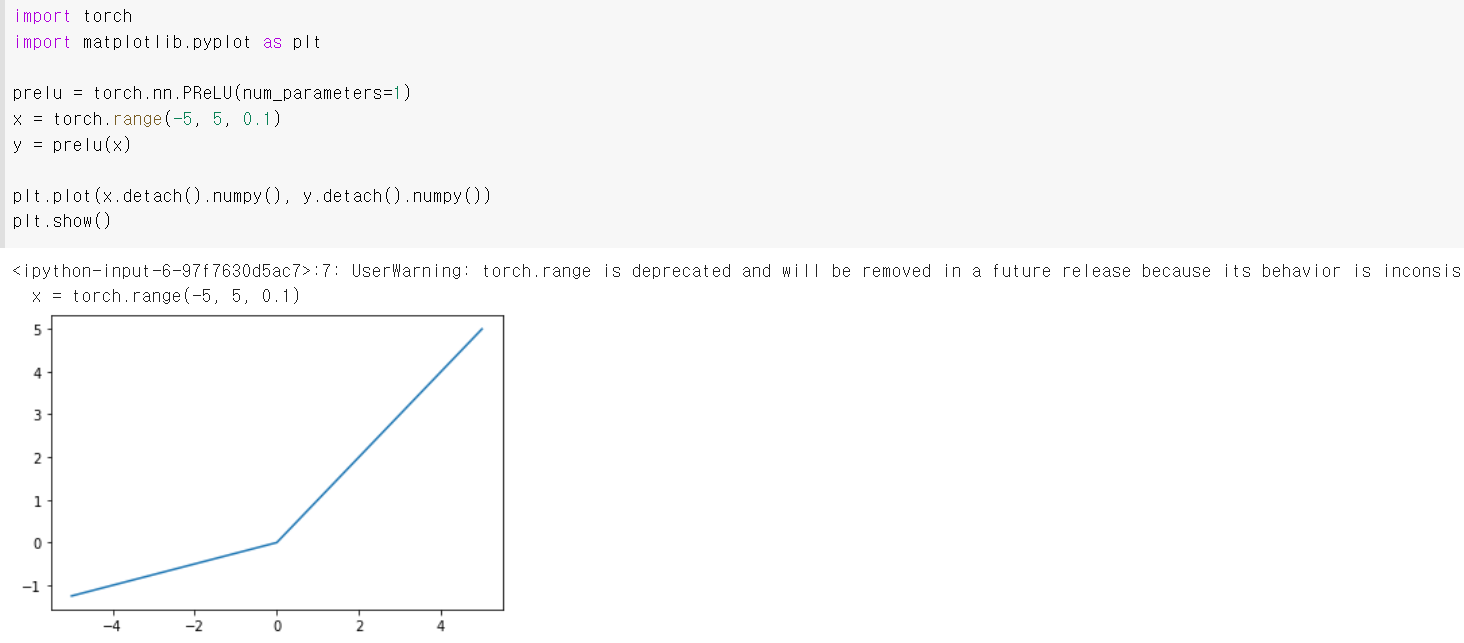
$x<0$ 에서 나타나는 gradient vanishing problem을 보완하는 LeackyReLU와 PReLU 활성화 함수를 개발했다.
PReLU : $f(x) =max(x, ax)$
LeackyReLU : $f(x) = max(0.1x, x)$

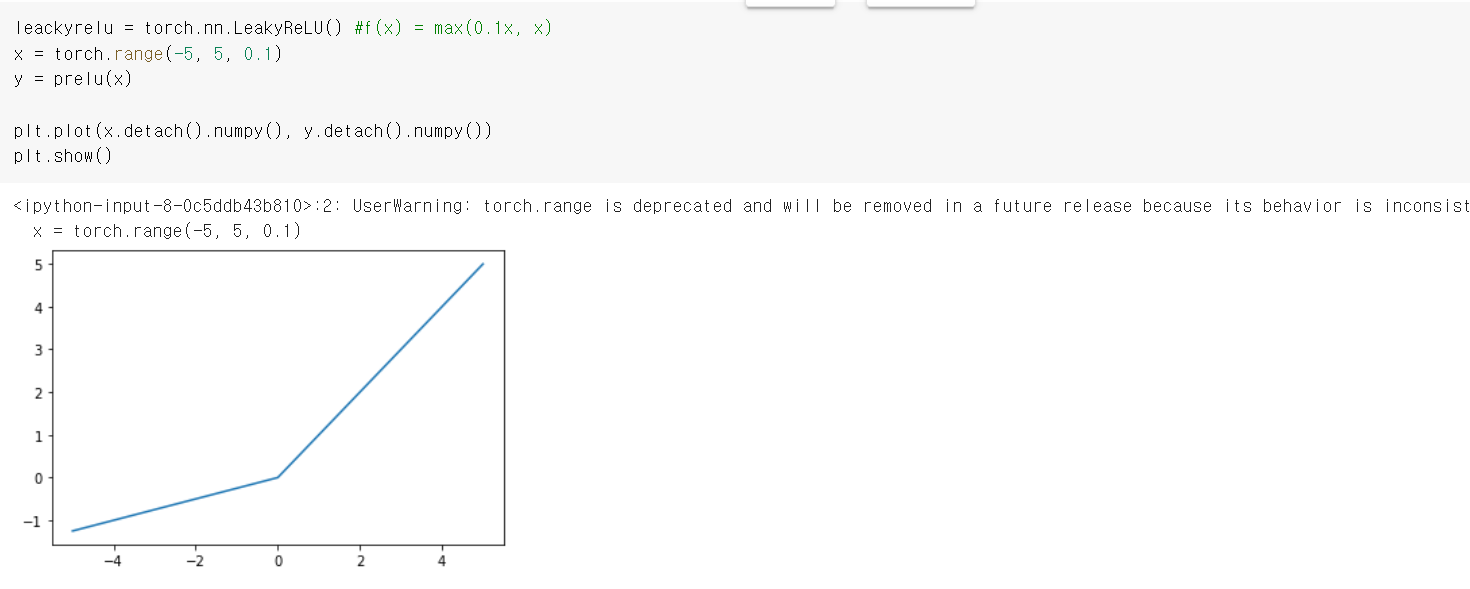
2.4 Softmax

Softmax는 sigmoid와 마찬가지로 output을 0과 1사이로 압축하여 확률을 나타낸다. 특히, Softmax는 각 출력의 합을 모든 출력의 합으로 나누어 k개의 class에 대한 이산확률분포를 만든다. 이때, Softmax를 적용한 output의 전체 합은 1이 된다.

$softmax(x_i)=$ $e^{x_i}\over\sum_{f=1}^{k} e^{x_f}$

💗이진 분류 문제(Binary classification)에서는 출력층의 activation function으로 sigmoid를, 다중 분류 문제(Multiclass Classification)는 softmax를 이용한다.

3. 손실함수

손실 함수는 정답 값(label, $y$ )과 예측 값(output, $\hat{y}$ )를 입력으로 받아 실숫값의 점수를 계산한다. 정답과 예측의 차이가 클수록 손실 함수의 점수가 높고, 모델 성능이 나쁘다는 것을 의미한다. PyTorch는 nn package 내에 여러 손실 함수를 구현해 놓았다. 많이 사용하는 몇 개의 손실함수를 살펴보고자 한다.

3.1 Mean Squared Error (MSE)

MSE는 예측과 정답의 차이를 제곱하여 평균한 값이다.

$L_{MSE}(y, \hat{y})={1\over n} \sum_{i=1}^{n}(y-\hat{y})$

torch.nn.MSELoss(size_average=None, reduce=None, reduction='mean')
코드에서 사용 예시는 다음과 같다. (임의의 3×5 tensor인 output, target를 정의하고 이 둘의 MSE를 계산하는 과정이다.)

import torch.nn as nn

criterion = nn.MSELoss()
output = torch.randn(3, 5, requires_grad=True)
target = torch.randn(3, 5)
loss = criterion(output, target)

이때, output과 target의 shape은 동일해야 한다.

3.2 Categorial Cross-Entropy

Categorial cross entropy는 일반적으로 다중 분류 문제(Multiclass Classification)에 사용한다.

$L_{cross-entropy}(y, \hat{y})=-\sum_iy_ilog(\hat{y}_i)$

K개의 class 분류 문제에서 신경망의 출력( $y$ )과 target( $\hat{y}$ )은 K개의 원소로 구성된 벡터이다. Cross Entropy는 이 두 벡터를 비교하여 손실을 계산한다. 위의 식에서 index $i$ 는 벡터의 $i$ 번째 원소를 뜻한다.

ex) Cost function for softmax $K=3$ 이면 label 즉, 정답값( $y$ )은 다음 세 벡터 중 하나이다.

$y=\begin{bmatrix}1\\0\\0\end{bmatrix}or \begin{bmatrix}0\\1\\0\end{bmatrix}or\begin{bmatrix}0\\0\\1\end{bmatrix}$

따라서, $L_{cross-entropy}(y, \hat{y})=-log(\hat{y}_j)$ , 이때, $j=true$ $class$ $index \in\{1, 2, 3\}$

Special Case, $K=2$ 인 경우를 생각해보자. Softmax를 적용한 output의 전체 합은 1이 되므로 $y_1+y_2=1$ , $\hat{y_1}+\hat{y_2}=1$ 이다. 따라서 다음 식이 성립한다.

$L_{cross-entropy}(y, \hat{y})=-(y_1log\hat{y}_1+y_2log\hat{y}_2)=-(y_1log\hat{y}_1+(1-y_1)log(1-\hat{y}_1))$

$y=\begin{bmatrix}1\\0\end{bmatrix}$ 즉, $y_1=1, y_2=0$ 을 위의 식에 대입하면 $L_{cross-entropy}(y, \hat{y})=-log\hat{y}_1$ 이 된다.
이때, $\hat{y}_1$ 가 1이 되면 cross-entropy는 0이 되고 $\hat{y}_1$ 이 0에 가까워질수록 무한대로 발산한다. 이처럼 cross entropy는 다른 class로 잘못 예측되는 정도가 클수록 더 많은 penalty를 준다. 따라서 Classification 문제에 적용하기에 적절하다.

torch.nn.CrossEntropyLoss(weight=None, size_average=None, ignore_index=-100, reduce=None, reduction='mean')

PyTorch에서 제공하는 Cross Entropy는 softmax를 합쳐놓은 것이므로 마지막 layer가 반드시 softmax일 필요는 없다.

import torch
import torch.nn as nn

criterion = nn.CrossEntropyLoss()
output = torch.randn(3, 5, requires_grad=True)
target = torch.tensor([1, 0, 3], dtype = torch.int64)
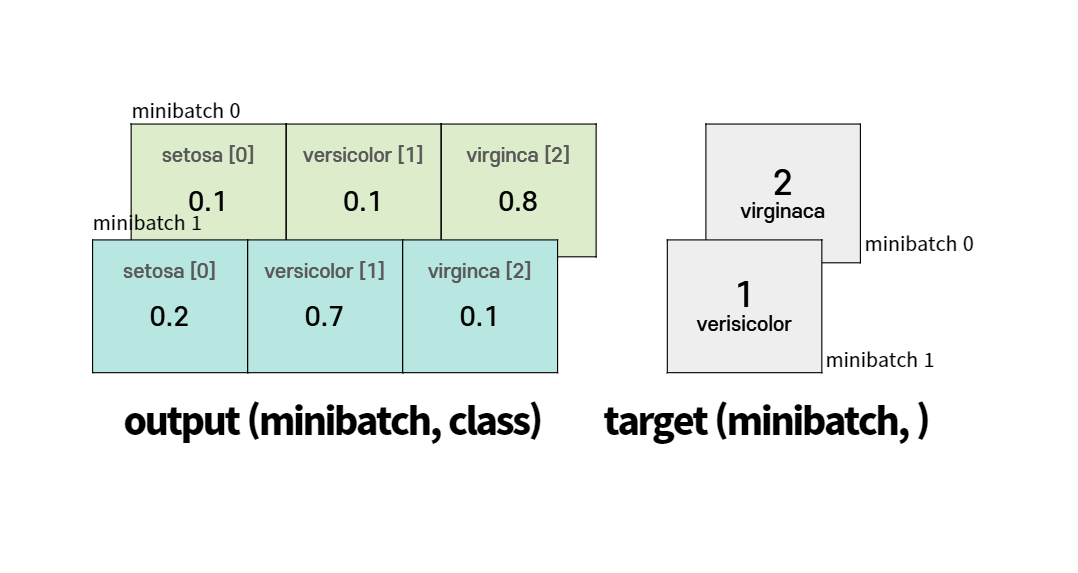
loss = criterion(output, target)

일반적으로 output의 shape은 (minibatch, Class) 이다. 그리고 target의 shape은 (minibatch, ) 이다.

예시 붓꽃을 3가지 종(setosa, Versicolor, Virginica)으로 분류하는 문제를 생각해보자.
이때, class의 개수는 3개이고 setosa는 0, versicolor는 1, virginaca는 2의 label이 주어진다. 이 경우에 output의 shape은 (minibatch, 3)이디. 그리고 각 minibatch의 target은 0, 1, 2 중 하나의 값을 갖는다.

3.3 Binary Cross Entropy

이진 분류에는 BCELoss를 사용하시는 것이 합리적이다.

torch.nn.BCELoss(weight=None, size_average=None, reduce=None, reduction='mean')

하지만, BCELoss에서는 softmax를 포함하지 않는다. 따라서, softmax 또는 다른 activation function을 따로 적용해주어야 한다. output과 target 모두 (minibatch, )의 shape을 가진다. 하나의 minibatch에서 softmax 또는 sifmoid를 거친 output은 0~1의 값을 가지며, target은 0또는 1의 값을 가진다.

import torch
import torch.nn as nn

criterion = nn.BCELoss()
sigmoid = nn.Sigmoid()                                    # 또는 nn.Softmax()
output = sigmoid(torch.randn(4, requires_grad=True))      # probabilities
target = torch.tensor([1, 0, 1, 0], dtype = torch.float32)

loss = criterion(output, target)