PyTorch Tutorial 03. Gradient Descent & AutoGrad

이 글은 한빛미디어의 '김기현의 딥러닝 부트캠프 with 파이토치'를 읽고 정리한 것입니다.

Gradient Descent

Cost function의 output의 최소로 만드는 parameter를 찾기 위해 기울기가 최소가 되는 값을 찾는 알고리즘

Deep Learning에서 Local Minuimum 문제

Local Minima 문제란, 우리의 목표인 global minimum이 아닌 local minimum에 도달하여 이 지점의 loss가 가장 작다고 판별하여 생기는 문제입니다. Local minimum에서도 gradient가 0이 되어 더 이상 update되지 않을 수 있기 때문입니다.

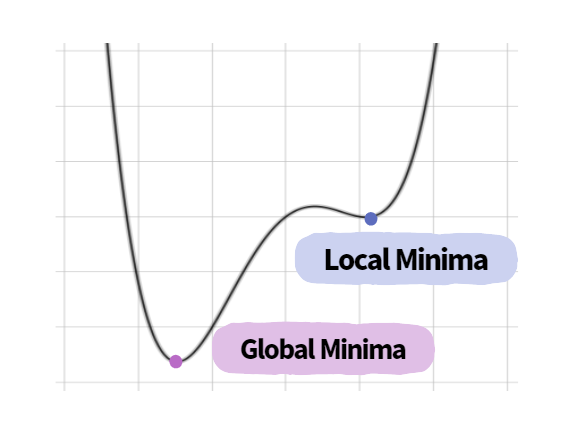
하지만, 고차원 공간에서는 local minimum이 큰 문제가 되지 않는다는 것이 학계의 중론입니다. 한 논문에서, 실제 딥러닝 모델에는 매우 많은 수의 weight가 있는데, 이 weight들이 모두 local minima에 빠져 update 정지가 될 확률을 매우 적다고 주장합니다. 또한, local minimum 문제가 발생한다고 하더라도 global minimum과 유사한 수준의 local minima이기 때문에 local minima 문제를 크게 고려할 필요는 없다고 주장합니다.

Learning Rate

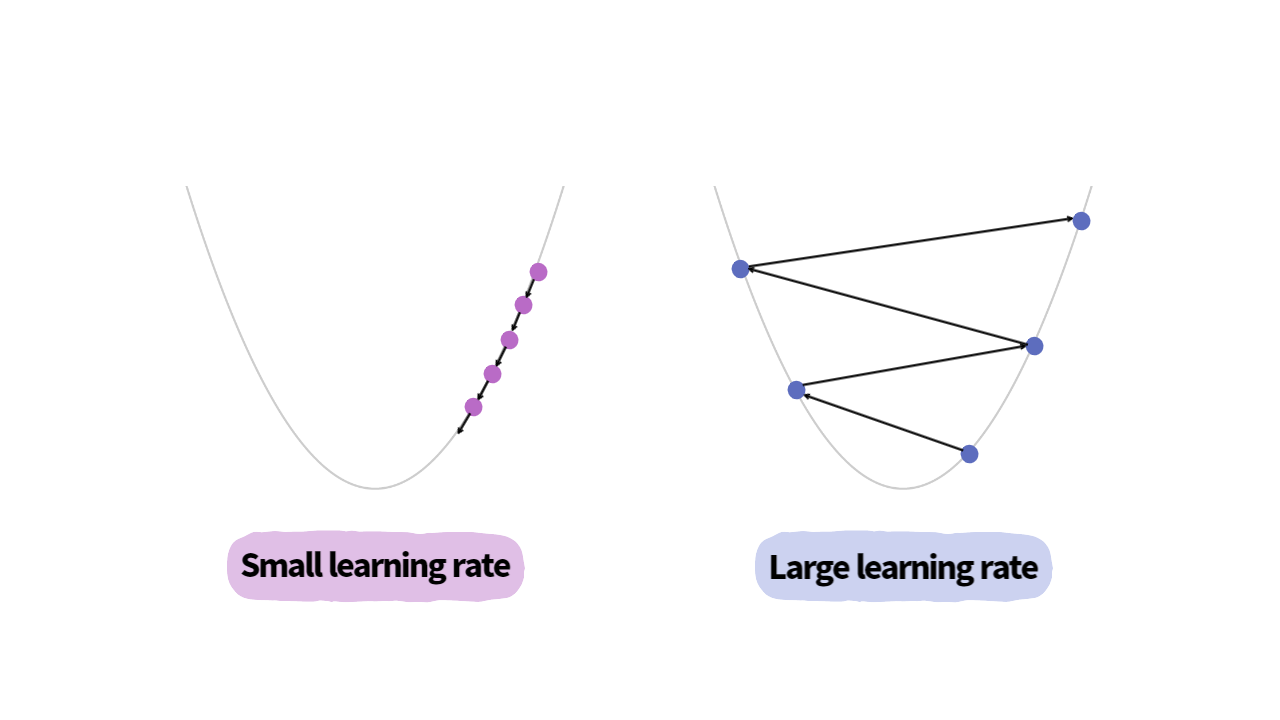
gradient descent algoritm을 수행할 때, 적절한 learning rate를 선정하는 것은 중요한 과제입니다. Learning rate가 너무 클 경우에는 parameter update 과정에서 loss가 발산할 가능성이 있습니다. 반면에, learning rate가 너무 작을 경우 수렴하기 위해 많은 학습 시간이 필요하다는 단점이 있습니다.

TORCH.AUTOGRAD

PyTorch에서는 gradient descent를 위한 Auto Grad 기능을 제공합니다.

PyTorch의 AutoGrad는 requires_grad = True 인 tensor의 연산을 추적하기 위한 계산 그래프(computational graph)를 구축합니다. 그리고 backward() 함수가 호출되면 그래프를 따라 미분을 자동으로 수행합니다.

requires_grad=True
해당 변수는 학습을 통해 계속 값이 변경되는 변수임을 의미합니다.

requires_grad 속성의 디폴트 값은 False이며 다음 코드 와 같이 해당 속성을 True로 만들 수 있습니다.

#1
x = torch.tensor([[1., 2.],
				  [3., 4.]], requires_grad = True)

#2
x = torch.FloatTensor([[1, 2],
					   [3, 4]]).requires_grad_(True)

requires_grad=True인 tensor로 여러 가지 연산을 수행한 결과 tensor 역시 모두 requires_grad 속성을 True로 갖게 됩니다.

위의 코드에서 생성된 결과 tensor 모두 grad_fn 속성을 가지고 있습니다. 수행한 연산에 따라 AddBackward(), SubBackward() 등으로 나뉩니다.

여기에 다음과 같이 backward() 함수를 호출하면 x, x1, x2, x3, y에 대한 gradient 값이 grad 속성에 저장됩니다.

x.grad를 제외한 나머지 인자의 grad가 None으로 저장되는 이유
grad 속성은 leaf tensor인 tensor의 것만 접근이 가능합니다. 예를 들어 위와 같은 상황에서 y = x3.sum()으로 정의되어 있지만, y를 연산할 때의 leaf tensor가 x인것을 자동으로 인식합니다. 따라서 y.backward()를 호출하면 leaf tensor인 x에 대한 y의 편미분 값이 계산되어 저장됩니다.

Gradient Descent 구현하기

Target y를 임의의 tensor로 정의하고 크기가 같은 tensor pred를 랜덤하게 생성합니다. 그리고 y와 pred의 loss function을 구하고 gradient descent를 활용하여 함숫값을 최소화합니다.

import torch
import torch.nn.functional as F

y = torch.FloatTensor([[.1, .2, .3],
                       [.4, .5, .6],
                       [.7, .8, .9]])  # target(label) tensor

pred = torch.rand_like(y)
pred.requires_grad = True
pred

[out] tensor([[0.4731, 0.1600, 0.5629],
    		  [0.2523, 0.2999, 0.1291],
    		  [0.3720, 0.8593, 0.8111]], requires_grad=True)
            

이때, 중요한 점은 값을 update할 y_pred의 requires_grad 속성을 True로 설정하여 update 가능하게 해야한다는 것입니다.

loss = F.mse_loss(y, pred)

그리고 두 tensor 사이의 loss를 구합니다. 이후, threshold와 learning rate를 설정해 loss가 threshold보다 작아질 때까지 미분 및 경사 하강법을 반복 수행합니다.

threshold = 1e-5
learning_rate = 1.
iter_cnt = 0

while loss > threshold : 
  iter_cnt += 1

  loss.backward() 

  pred = pred - learning_rate * pred.grad

  pred.detach_()
  pred.requires_grad_(True)

  loss = F.mse_loss(pred, y)

  print('%d-th Loss : %.4e' % (iter_cnt, loss))

  print(pred)

pred.detach_() 함수는 pred의 gradient 정보를 초기화 합니다. 그 후 pred.requires_grad_(True)을 통해 requires_grad 속성을 다시 True로 만들어 학습이 가능한 변수로 만들어줍니다.

반복적인 학습 과정에서 gradient를 초기화하는 이유
PyTorch에서 gradient는 기본적으로 누적되어 저장되기 때문에, 이전에 계산된 gradient 값이 backward 연산 중에 새로운 gradient 값과 더해집니다. 만약 이전에 계산된 gradient 값이 업데이트를 방해하는 큰 값이거나, 새로운 gradient 값이 작은 값이라면, 이전에 계산된 gradient 값이 새로운 gradient 값에 큰 영향을 미치게 됩니다. 이러한 상황은 모델이 수렴하지 못하고, 학습이 불안정해지는 원인이 될 수 있습니다.

[전체 코드]

import torch
import torch.nn.functional as F

y = torch.FloatTensor([[.1, .2, .3],
                       [.4, .5, .6],
                       [.7, .8, .9]])  # target(label) tensor

pred = torch.rand_like(y)
pred.requires_grad = True

loss = F.mse_loss(y, pred)


threshold = 1e-5
lr = 1.
count = 0

while loss > threshold :
  count += 1

  loss.backward()

  pred = pred - lr * pred.grad

  pred.detach()
  pred.requires_grad_(True)

  loss = F.mse_loss(y, pred)

  print("%d-th Loss: %.4e" %(iter_count, loss))
  print(pred)