
1. Unsupervised Learning (비지도 학습)
Label(정답)이 없는 data를 학습하는 방법
- clustering(군집화)는 대표적인 비지도 학습
- 이외에 차원 축소, 생성 모델 등 다양한 방법 존재
Clustering
Label이 없는 data들 내에서 비슷한 특징이나 패턴을 가진 data들 끼리 군집화한 후 어떤 군집에 속하는지 추론하는 방법
(대표적인 Clustering Algorithm으로 K-Means Clustering이 있다)
2. K-Means Clustering
값이 주어져 있을 때, 개의 데이터들을 개의 클러스터로 묶는 알고리즘
- : 군집의 수 (number of cluster)
- : 평균
(데이터의 평균을 활용하여 개의 군집으로 묶는다는 의미)
Initialization
random으로 개의 centeroid 를 생성 { }
특정 조건이 발생할 때까지 다음 2 step을 반복
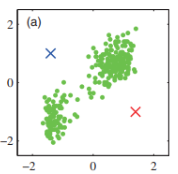
Assignment step
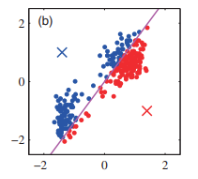
각 데이터의 cluster membership을 결정
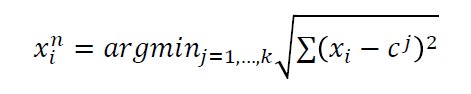
Refitting step
각 centroid를 cluster member의 중심으로 이동
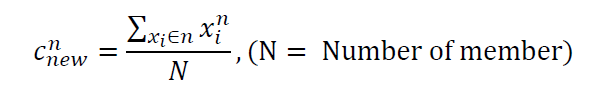
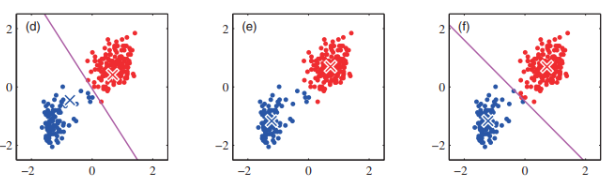
Result
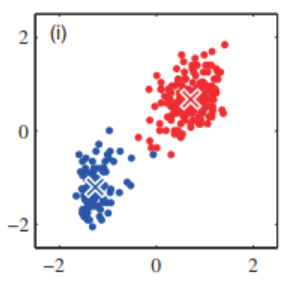
Local minima 문제
Kmeans Algorithm은 Centroid의 초기 상태에 따라 성능이 달라질 수 있음
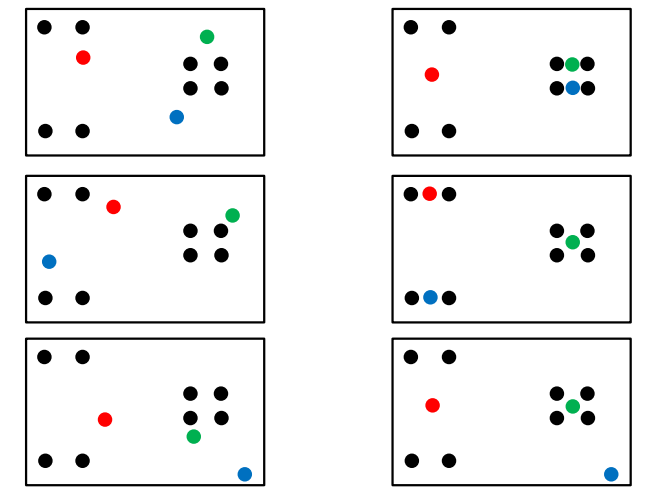
3. K-Means Clustering 실습
: Hard Coding / sklearn을 이용한 Coding
데이터 생성
import numpy as np
import matplotlib.pyplot as plt
data=[]
for i in range(30):
data.append([np.random.uniform(40,60), np.random.uniform(40,60),0])
data.append([np.random.uniform(50,120), np.random.uniform(50,120), 1])
data.append([np.random.uniform(100,190), np.random.uniform(90,160), 2])
data=np.array(data)
plt.scatter(data[:,0], data[:,1])
plt.show()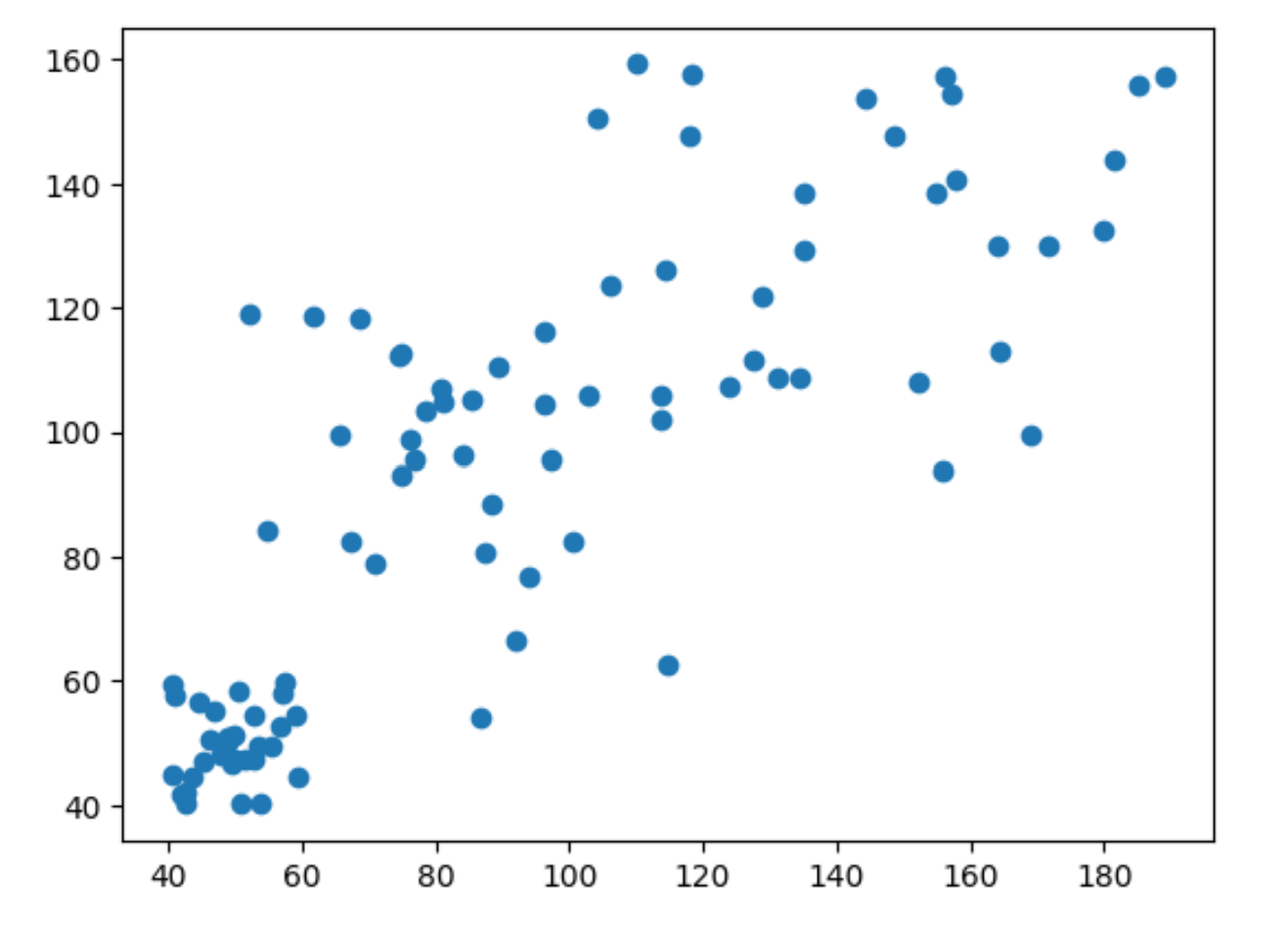
Centroid initialization
값을 받아서 centroid 개를 만들고 Numpy Random을 이용하여 각 centroid 의 position 초기화
def initialization(k):
centroid=[]
for i in range(k):
centroid.append([np.random.uniform(4,190), np.random.uniform(4,190)])
return np.array(centroid)
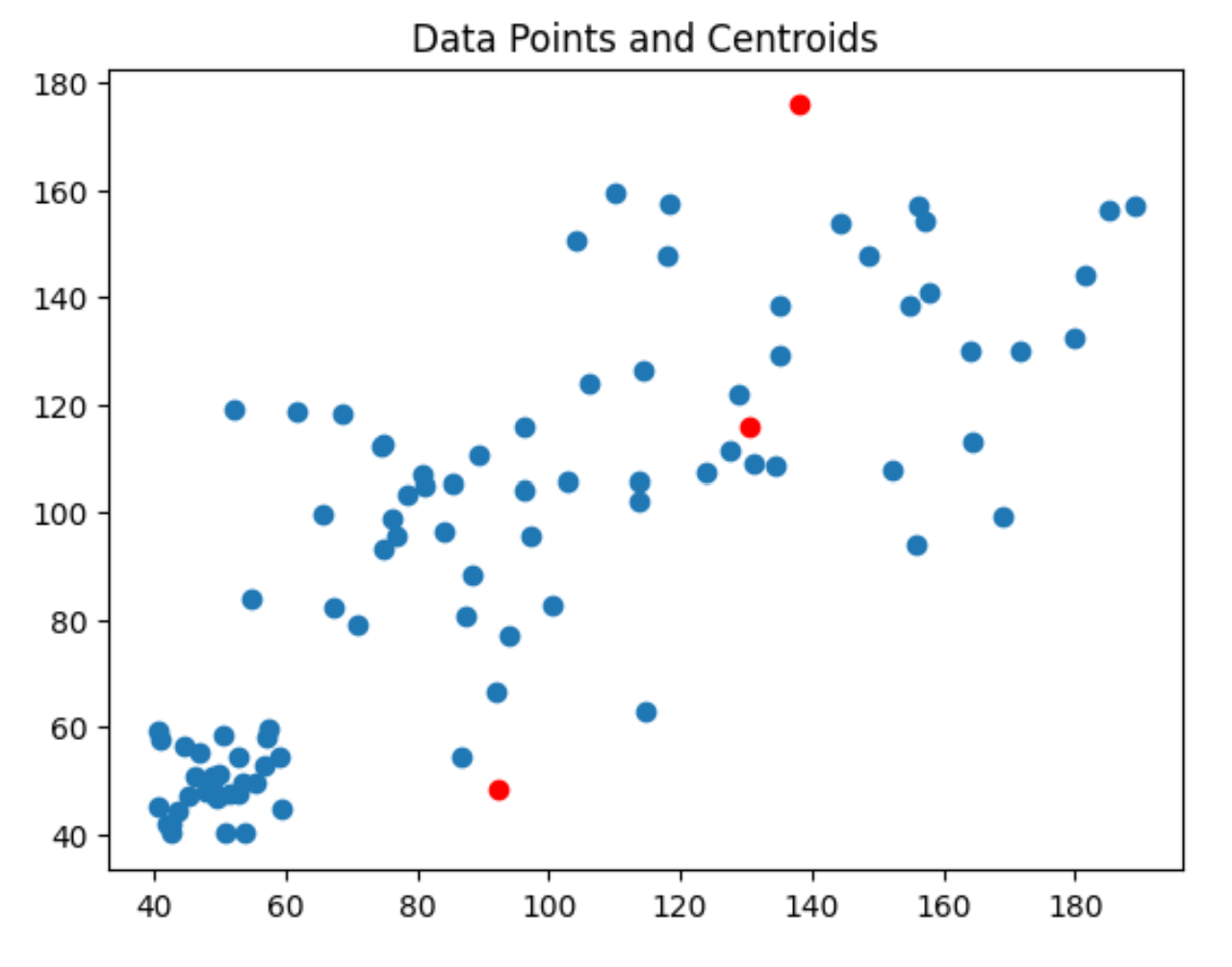
centroid = initialization(3)
print(centroid)
plt.scatter(centroid[:, 0], centroid[:, 1], color='red')
plt.scatter(data[:,0], data[:,1])
plt.title('Data Points and Centroids')
plt.show()
Distance function
두 변수 a,b가 입력되면 변수 간에 거리를 계산하여 return 하는 함수
(np.sum을 사용함으로써 feature의 수가 뭐든 사용할 수 있음)
def distance(a,b):
return np.sqrt(np.sum((a-b)**2))K-Means Algorithm
def k_means(data, centroid):
k=len(centroid)
n=len(data)
x_n=[]
#assignment step
for i in range(n):
D=[0]*k
for c in range(k):
D[c]=(distance(data[i, 0:2], centroid[c, :]))
x_n.append(np.argmin(D))
x_n=np.array(x_n)
#refitting
for i in range(k):
index=np.where(x_n==i)[0]
mu=np.mean(data[index, 0:2], axis=0)
centroid[i]=mu
return centroid, x_n
for i in range(50):
new_centroid, x_n = k_means(data, centroid)
plt.scatter(new_centroid[:, 0], new_centroid[:, 1], color='red')
plt.scatter(data[:,0], data[:,1])
plt.title(f'Loop = {i} Data Points and Centroids')
plt.show()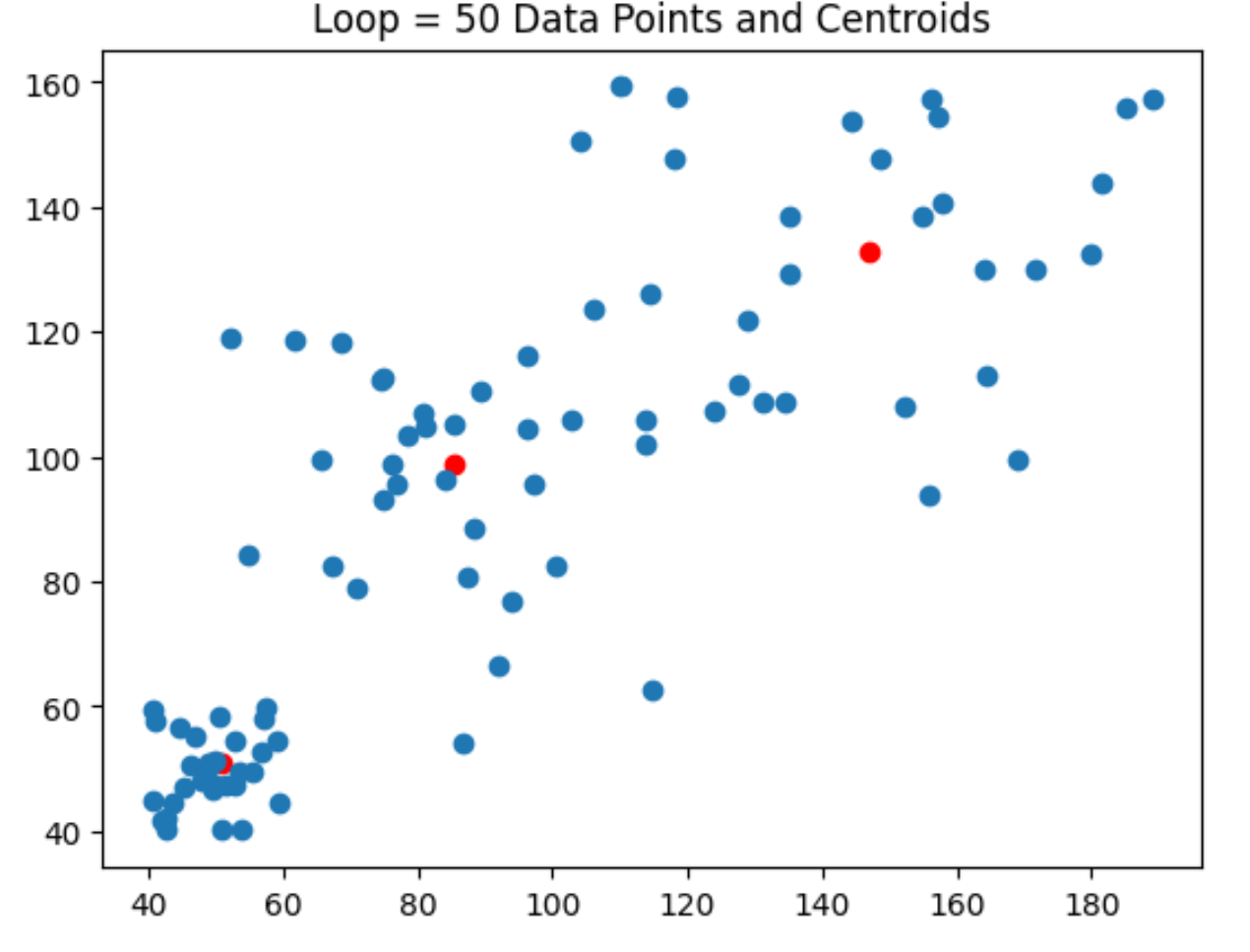
print(new_centroid)
4. Elbow Method
: K-means에서 최적의 군집 수를 찾는 방법
군집 수를 어떻게 설정하느냐에 따라 Model 성능이 결정된다.
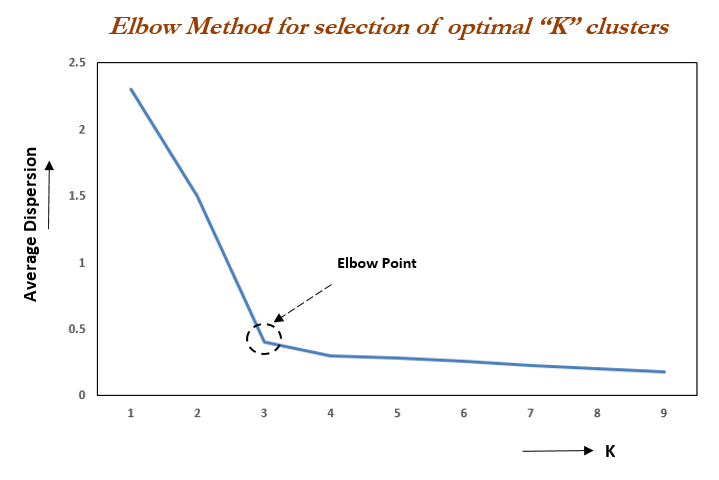
최적의 군집 수를 찾기 위해 사용하는 방법으로 군집 내 총 제곱합 (WCSS : Within Cluster Sum of Squares)을 구함
(팔꿈치처럼 꺽여있는 부분이 최적의 point)
Example
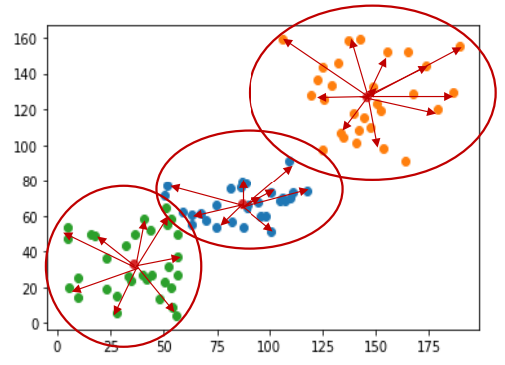
이라면, WCSS는 다음과 같다.
3개의 군집에 대하여 각 Centroid와 data의 거리를 합산한 값을 계산
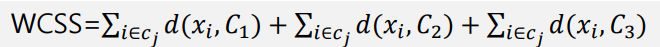
Elbow Method 문제점
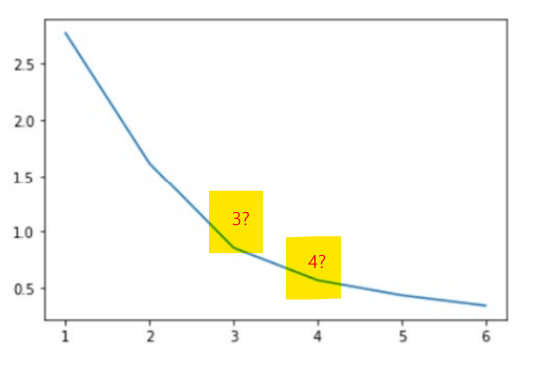
적당한 값을 찾는 것이 목표이지만 모호한 결과가 나올 수 있다.
위의 사진 처럼 중에 어떤 것이 최적의 Elbow point인지 판단하기 어렵다.
5. Silhouette Method
: cluster를 평가하는 지표
Elbow method의 문제점을 해결하기 위해 사용하는 cluster 평가 지표
개별 데이터가 다른 군집 내 다른 데이터와 얼마나 멀리 분리되어 있는지 수치로 나타낸 것
실루엣 계수 계산
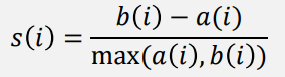
: 동일한 군집 내 다른 데이터들과의 평균 거리
: 가장 가까운 다른 군집 내 데이터들과의 평균 거리
Step 1. 군집 A의 데이터 를 선택
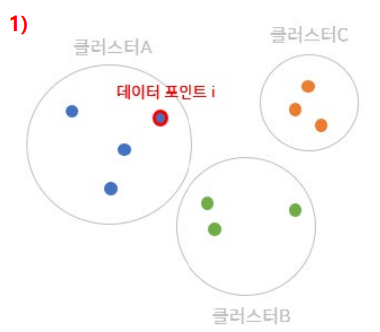
Step 2. 동일한 군집 내 다른 데이터들 간 평균 거리 구하기
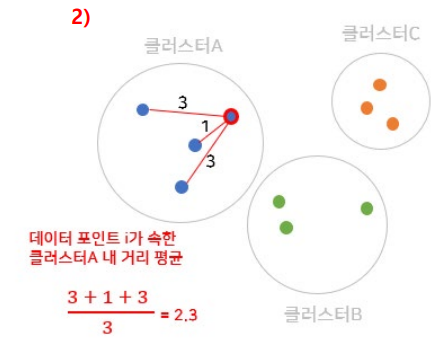
Step 3. 데이터 와 다른 군집 내 데이터 간 거리 평균 구하기
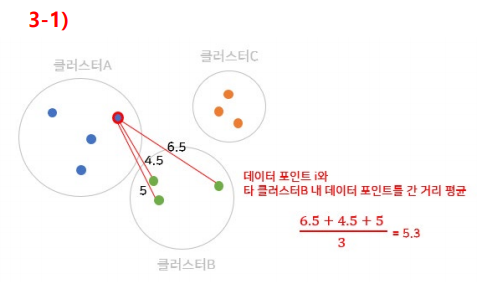
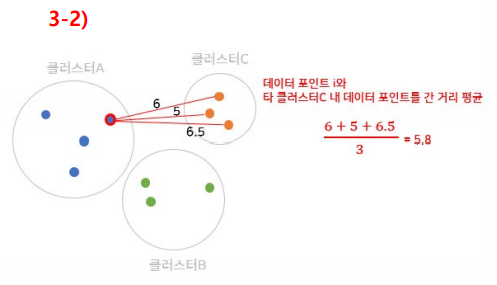
Step 4. 와 가장 가까운 군집을 구하기
Step 5. 데이터 와 다른 군집 내 데이터 간 거리 평균 구하기
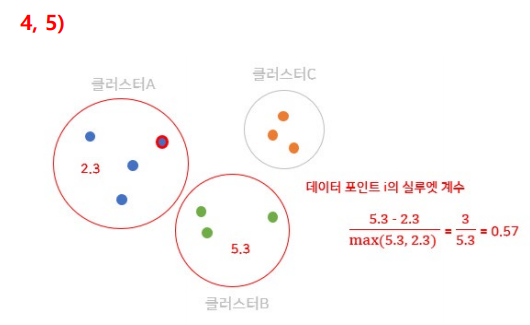
Step 6. 모든 데이터에 대해 전체 과정을 반복하여 실루엣 계수 구하기
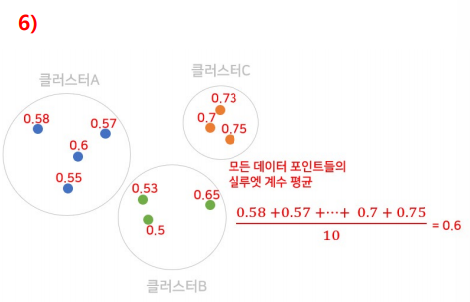
실루엣 계수 평가
사이의 값을 가질 수 있음
- 가 1에 가까울 수록 군집화가 잘 된 상태
- 가 0에 가까울 수록 두 군집 간 구분이 잘 안 된 상태
- 가 음수일 경우, 이웃 클러스터에 더 가까운 상황(최악)
Silhouette Method 장단점
장점
- 클러스터링이 수행된 후 실루엣 계수를 구하기에 클러스터링 알고리즘에 영향을 받지 않음
- 적절한 클러스터 개수를 정할 때 효과적인 방법
- 클러스터링 결과를 시각화할 수 있음
단점
- 데이터 양이 많을 수록 오래 걸림
(최적의 k값을 정하기 위해 모든 경우의 수를 다해봐야 하는 NP-hard문제로 Time complexity가 높아짐)
