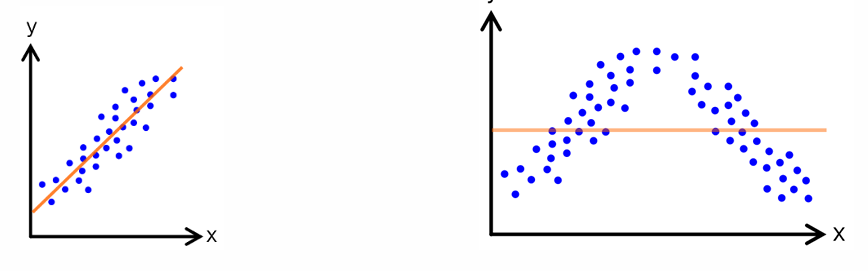
1. 차원의 저주 (The curse of dimensionality)
차원이 증가하면서(=feature 개수) 문제 공간이 기하급수적으로 커지는 현상
- 용량이 커져서 많은 메모리 필요
- 관측치 보다 feature 수 많아짐 -> 모델 성능 저하
- 데이터 사이의 거리가 멀어지고 빈 공간 생김 -> sparsity 문제 발생
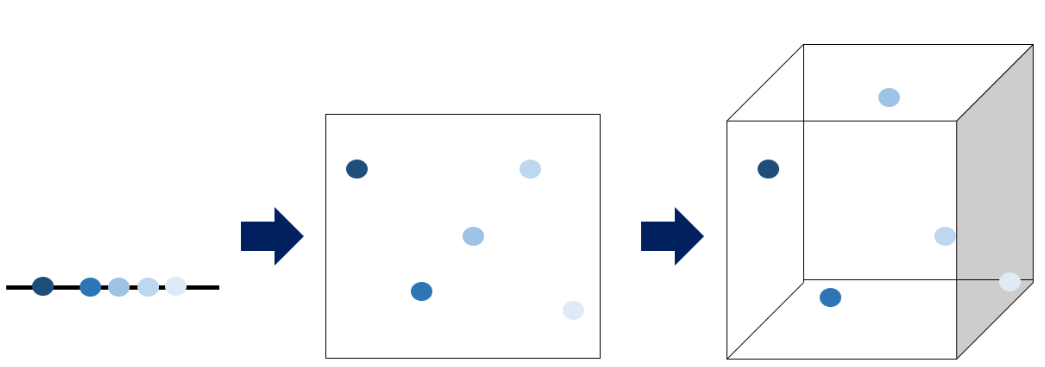
2. 차원 축소
차원 축소는 고차원의 데이터를 저차원의 데이터로 변환하는 방법(-> 사용되는 feature를 줄이는 것)
차원 축소를 하는 이유
- 비용, 시간, 자원, 용량 문제 해결
: 차원의 저주 문제 해결 - 과적합 문제 해결
: 변수가 많으면 모델 복잡도 증가, 과적합 발생 - 설명력 증가
: 차원이 낮으면 내부 구조 파악 및 해석이 쉬움(시각화 가능해서)
차원 축소의 단점
- 간소화 한 만큼 정보 손실 생김
대표적인 차원 축소 알고리즘
- 주성분 분석 (PCA : Principal Component Analysis)
- LDA (Linear Discriminant Analysis)
- LLE (Locally Linear Embedding)
- MDS (Multidimensional Scaling)
- Isomap
- t-SNE (t-distributed Stochastic Neighbor Embedding)
3. PCA를 위한 개념
: 정사영/투영(projection), 선형변환, 차원축소와 분산, 공분산, 고유값/고유벡터
차원 축소와 분산
: 두 개 이상의 feature를 합쳐 하나로 만들 때, 데이터의 분산을 유지하면 데이터의 특성을 유지할 수 있다!
(데이터 간 분산을 최대로 유지하면, 정보의 손실을 최소화 가능)
- 분산(Variance) : 데이터가 퍼져있는 정도
- 엔트로피(Entropy) : 물질이 분산되는 정도, 분포가 가지는 정보의 확신도
공분산
2개의 확률변수의 선형관계/상관정도(correlation)을 나타내는 값
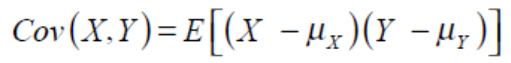
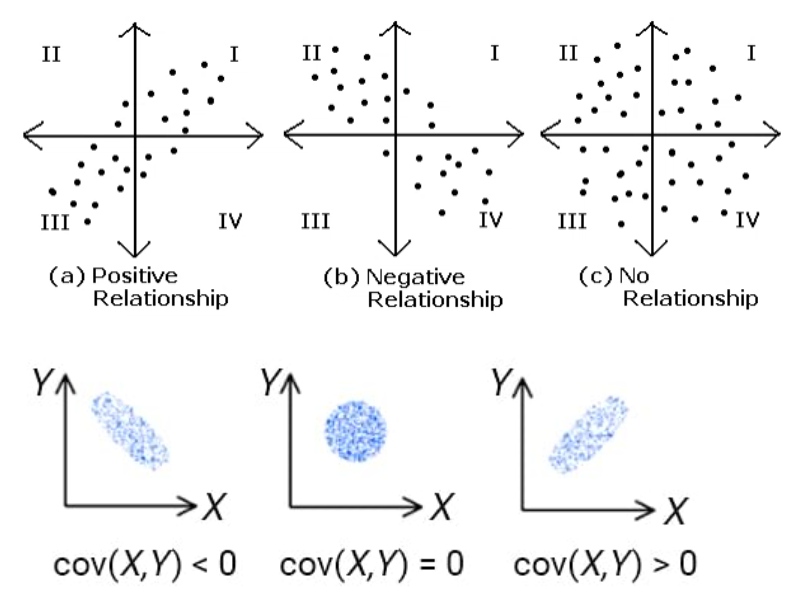
- (a) : X가 증가/감소할 때 Y가 반드시 증가/감소 -> 공분산(>0)
- (b) : X가 증가/감소할 때 Y가 반드시 감소/증가 -> 공분산(<0)
- (c) : X의 증가/감소에 상관없이 Y의 데이터가 분포 -> 공분산=0
고유값과 고유벡터
lambda : 고유값 / x : 고유벡터
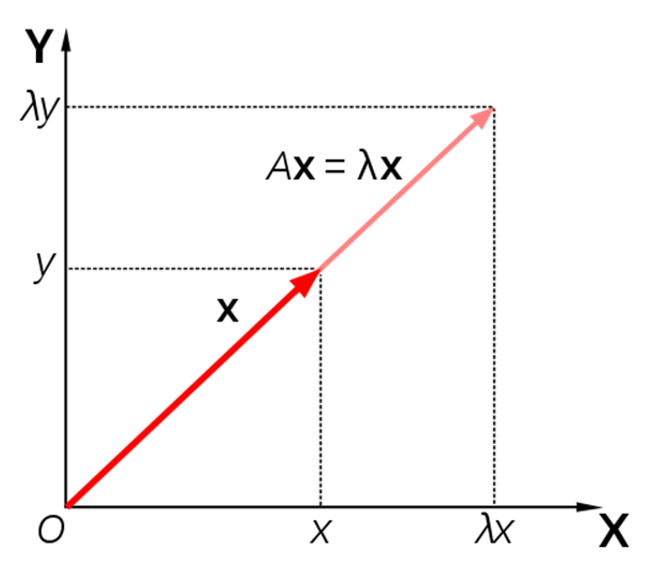
고유벡터 (x)
- 행렬이 벡터의 변화에 작용하는 주축의 방향을 나타냄
- 공분산 행렬의 고유벡터는 데이터가 어떤 방향으로 분산되어 있는지 나타냄
고유값 (λ)
- 고유벡터 방향으로 얼마 만큼의 크기로 벡터 공간이 늘려지는지를 나타냄
- 고유값은 여러 해가 존재할 수 있으며, 값이 큰 순서대로 고유 벡터를 정렬하면 결과적으로 중요한 순서대로 주성분을 구할 수 있음
4. 주성분 분석(PCA)
주성분 분석 목적
: 고차원 데이터를 분산이 최대로 보존되는 저차원의 축 평면으로 투영하여 차원 축소
- 목표 : 분산이 최대로 보존되는 축을 어떻게 찾을 것인지
- 방법 : 입력 데이터들의 공분산 행렬에 대한 고윳값 분해
Overview
1) 분산이 가장 작은 방향으로 첫 번째 축을 생성하여 사영 (첫 번째 데이터 feature 생성)
2) 첫 번째 축에 직각이 되는 벡터를 두 번 째 축으로 하여 사영(두 번째 데이터 feature 생성)
3) 두 번째 축에 직각이 되는 벡터를 세 번째 축으로 하여 사영(
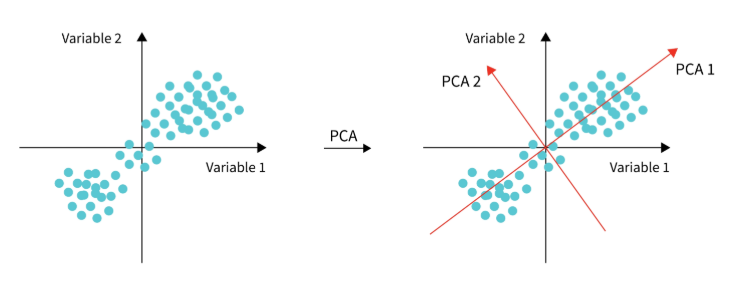
주성분 분석 Summary
1) 데이터 정규화(표준화)
2) Covariance matrix 계산
3) Covariance matrix로부터 고유값 계산
4) 고유 벡터 구하기
5) 고유벡터를 고유값의 순서대로 나열
6) 고유벡터를 1)에서 구한 기존 데이터에 적용하여 변환
(이때 elbow point / 정보량 기준으로 데이터 선택)
5. 주성분 분석 Example
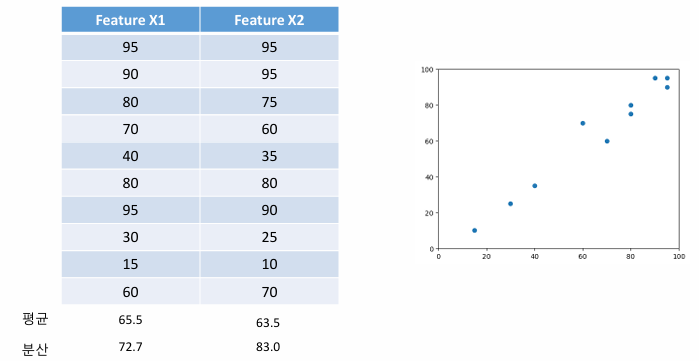
1) 데이터 정규화(표준화)
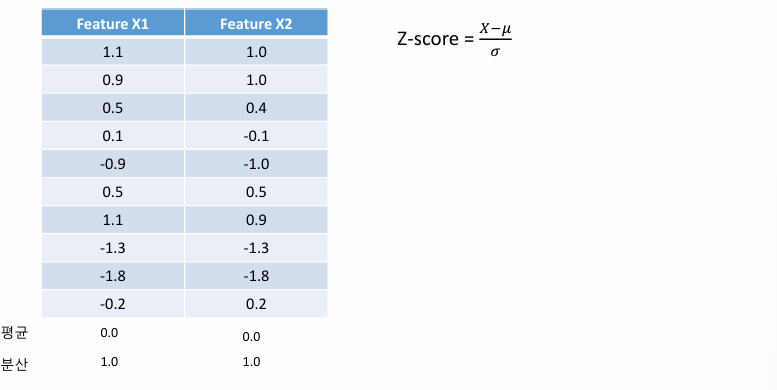
2) Covariance Matrix 구하기
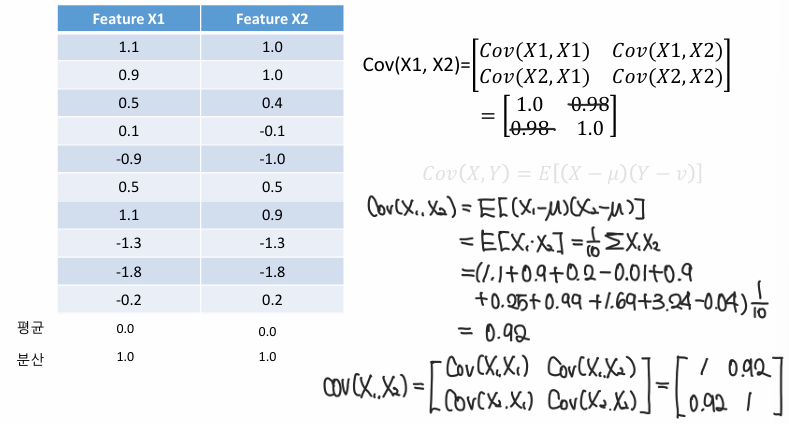
3) 고유값 구하기
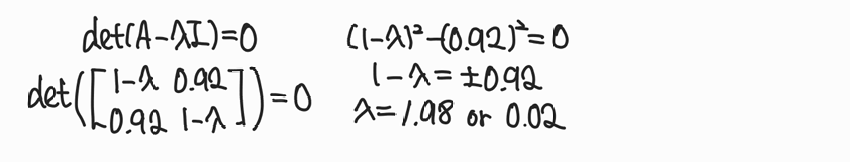
4) 고유벡터 구하기
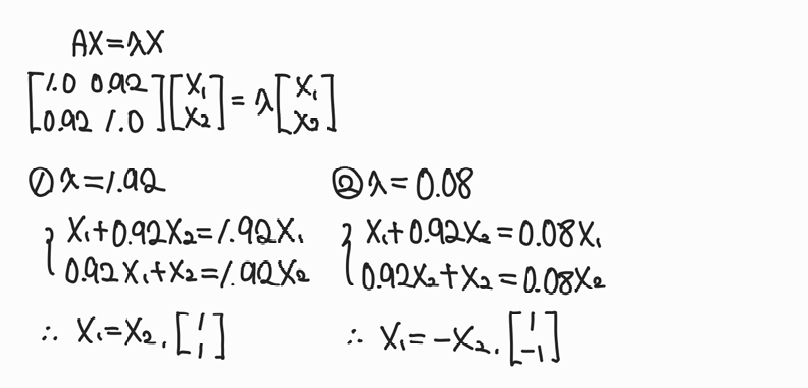
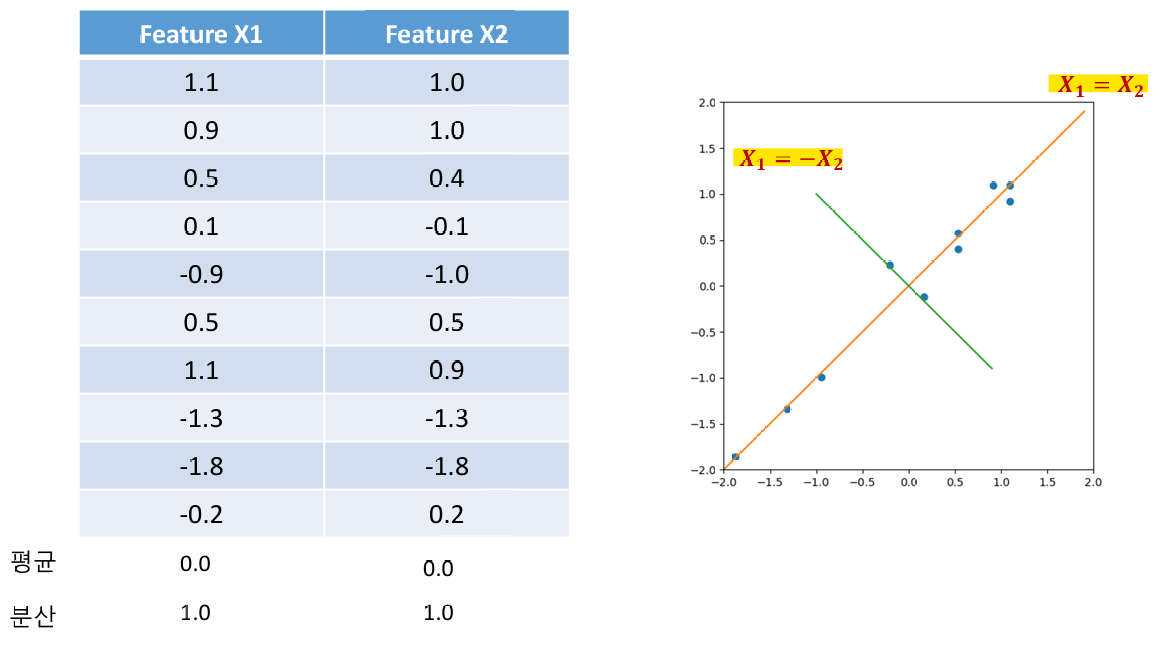
5) 데이터 표현하기
6) 고유벡터를 1)에서 구한 기존 데이터에 적용하여 변환
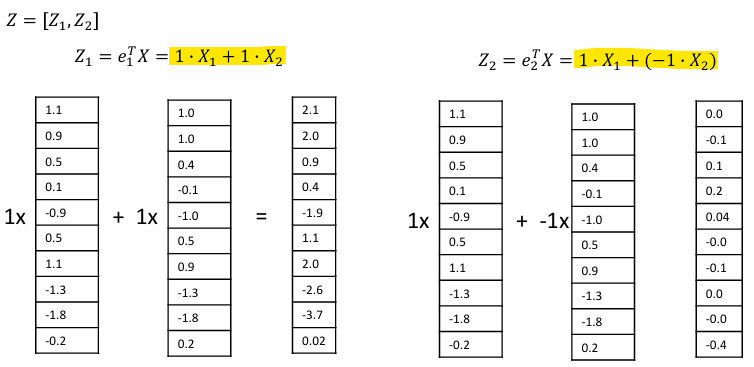
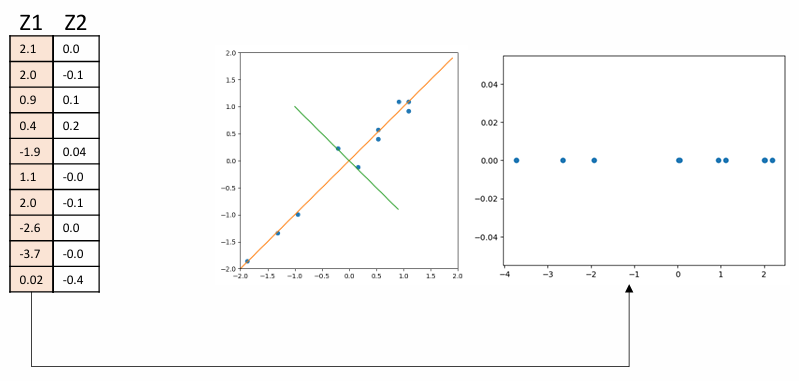
주성분 분석 한계
1) 데이터 분포가 비선형일 경우, 적용하기에 까다로움
(대안 : LLE (Locally Linear Embedding))
2) 분류 문제의 경우, 데이터의 범주 정보를 고려하지 않기에, PCA를 취한 뒤 범주 분류가 더 잘 되도록 변환되는 것은 아님
(대안 : PLS (Partial Least Square))