Big Data Analytics #03 Dimensionality Reduction2: T-SNE

PCA 차원 축소의 한계점 Big Data Analytics #01 Data Cleaning

• 선형 분석 방식으로 값을 투영하기에, 군집화 되어 있거나 비선형 데이터에 올바른 동작 어려움
  

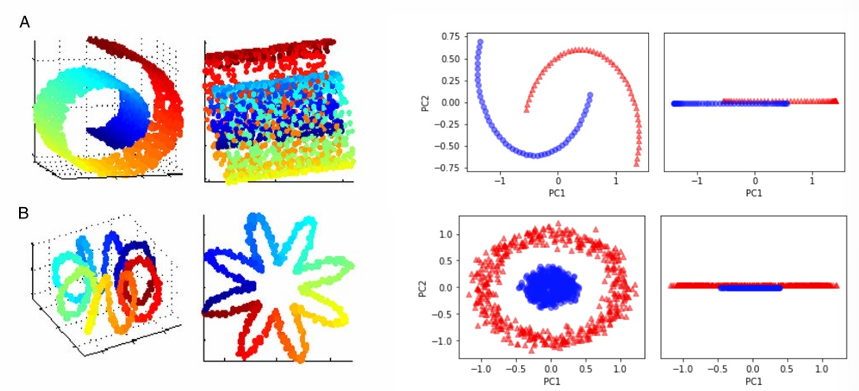
(대안으로 T-sne 나옴)

1. T-SNE 개요

: T-distributed Stochastic Neighbor Embedding

높은 차원의 데이터를 저차원으로 축소하는 방법
(비선형 데이터에 대해서도 잘 동작하는 장점을 가짐)

고차원에서 가까운 데이터는 저차원에서도 가까울 것이며,
멀리 떨어진 데이터는 저차원에서도 멀리 떨어져 있을 것

• 거리의 개념 : 이웃하다 → Neighbor embedding
• 판단의 근거 : 확률적으로 Stochastic
• 확률 분포의 기준 : T distribution

Overview

1) 고차원 데이터에서 유사한 점 찾기
2) 저차원 공간에서 유사한 점 배치하기
3) 두 확률 분포(P,Q) 차이를 줄이기 (KL Divergence로 최소화)
4) 최적화가 완료되면 데이터 구조 시각화

2. Stochastic Neighbor Embedding (SNE)

SNE의 목표

고차원에서의 데이터 분포와 저차원에서의 데이터 분포를 같게 만드는 것

Probability $P$

고차원 데이터에서 유사도 확률 분포
: 특정 데이터 포인트 $x_i$가 주어졌을 때, 다른 데이터 포인트 $x_j$를 선택할 확률을 가우시안 분포를 이용해 계산
(σ는 특정 데이터 포인트의 perplexity를 조정하기 위해 설정되는 표준 편차)

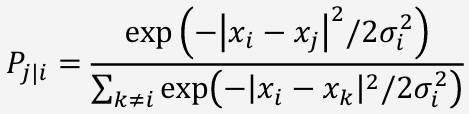
Perplexity

"한 점이 몇 개의 이웃을 고려할지"에 대한 기준 (희망하는 복잡도)

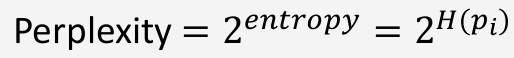
• Perplexity 작은 경우 : 가까운 이웃(국소적인 구조) 중심으로 학습
• Perplexity 큰 경우 : 멀리 있는 점들(전역적인 구조)도 고려

Perplexity와 표준편차 σ 조정

목표 : Perplexity 값을 설정한 후, 조건부 확률 $P$ 의 엔트로피 $H(P)$ 가 Perplexity와 맞추기

1) 초기값 설정 : σ의 초기값 설정 (보통 1부터 시작)
2) 조건부 확률 $P$ 계산 : 현재 σ 값으로 $P$ 확률 계산 후 Entropy 계산

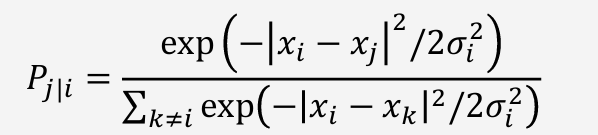
3) 이진 탐색을 통한 σ 조정

• $H(p) > log_2(perplexity)$ → σ 줄이기
  (데이터를 더 집중시킴, 밀집 데이터에 집중)
• $H(p) < log_2(perplexity)$ → σ 늘리기
  (데이터를 더 넓게 퍼트림, 희소 데이터 포함)

Cost Function

Kullback-Leibler Divergence (KL divergence)

고차원 공간과 저차원 공간의 두 확률 분포 $P, Q$가 얼마나 비슷한지 측정하는 지표

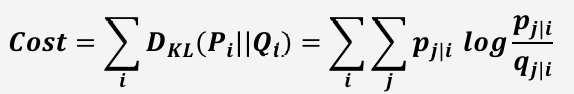
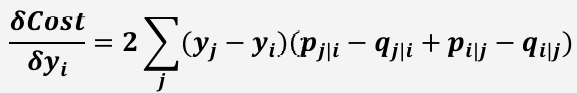
SNE의 한계점

• KL divergence 비대칭 문제
  고차원에서는 가까운 점들(p가 큰 것)을 신경 쓰고, 저차원에서 먼 점들은 덜 신경 씀
  → 가까운 점들만 보존, 멀리 떨어진 점들은 잘 표현 X
  (클러스터 간 간격이나 전체적인 구조를 왜곡)
• 가우시안 확률 분포를 가정하여 발생하는 문제
  : 저차원에서는 거리 차이가 작게 나타나는 경향이 있음
  (가우시안 분포는 꼬리가 얇아서, 먼 거리의 점들 간 확률이 거의 0이 됨 → 멀리 있는 점들의 관계 표현이 힘들어짐)

(이것을 해결한 것이 TSNE)

3. T-distributed Stochastic Neighbor Embedding (T-SNE)

T distribution 사용

고차원에서 유사도가 작은 값들이 많기에, 가우시안 분포를 사용하면 정보 손실 일어남

사진 출처

T distribution은 꼬리가 두꺼워, 저차원 공간에서 작은 거리 차이를 더 잘 반영할 수 있음

KL divergence 의 비대칭 문제 해결

$P$ 가높고 $Q$ 가낮을때에는 cost가높지만 $P$ 가 낮고 $Q$ 가 높을 때에는 cost가낮음

Cost Function을 $P, Q$에 대해 대칭적으로 만들기 위해 아래와 같이 계산

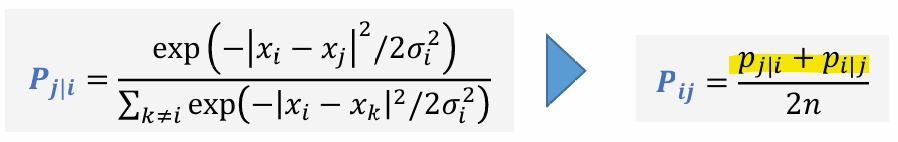
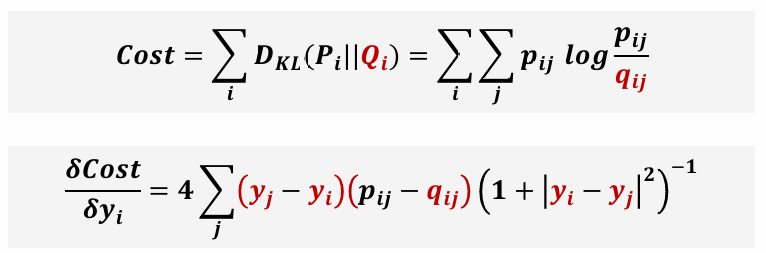
4. Evaluation : Perplexity

: Perplexity 값에 따라 성능이 달라질 수 있음

Perplexity는 하나의 정답이 있는 값이 아니라, 여러 시도를 거쳐 최적의 구조를 찾아야 하는 값

일반적인 경우

Perplexity 5~50값을 추천(기본값=30)
너무 큰 값일 경우 dataset의 모든점을 균일하게 취합하여 군집이 무너짐

군집의 크기가 다른 경우

Perplexity가 클수록, 군집의 크기를 비슷하게 보이도록 학습
( $P, Q$ 분포가 같아지도록 학습하기에 )
→ 원래 군집의 진짜 크기를 왜곡할 수 있음

군집의 거리가 다른 경우

Perplexity가 커질수록, 멀리 떨어진 군집 간 거리를 가깝게 표현하려 함
→ 원래 데이터의 구조(거리)가 손상될 수 있음

5. T-SNE 실습

: Sklearn을 이용한 Coding

데이터 불러오기

from sklearn.manifold import TSNE
from sklearn.datasets import load_digits
import matplotlib.pyplot as plt

digits=load_digits()

fig, axis=plt.subplots(2,5, figsize=(10,5), subplot_kw={'xticks':[], 'yticks':[]})

for ax, imgs in zip(axis.ravel(), digits.images):
    ax.imshow(imgs)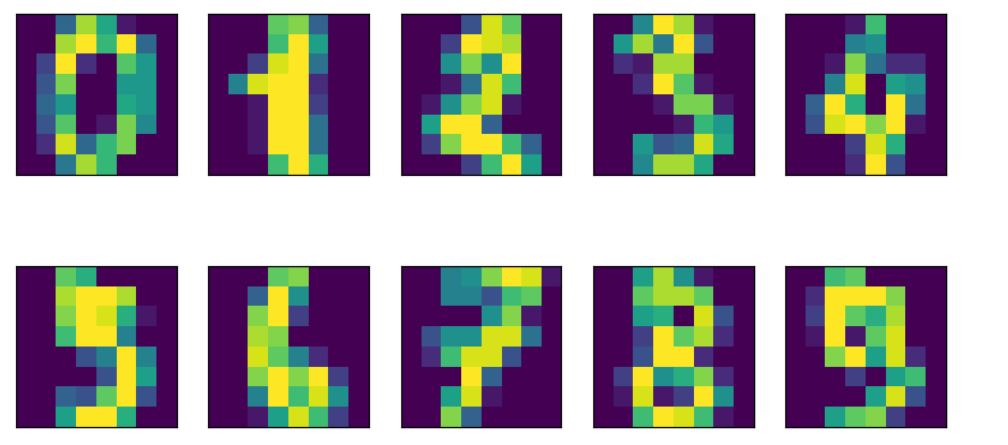

TSNE 모델 학습하기

tsne=TSNE()
digists_tsne=tsne.fit_transform(digits.data)
print(digists_tsne.shape)

plt.figure(figsize=(10,10))
plt.xlim(digists_tsne[:,0].min(), digists_tsne[:,0].max()+1)
plt.ylim(digists_tsne[:,1].min(), digists_tsne[:,1].max()+1)

colors = ['black', 'blue', 'purple', 'green', 'red', 'brown', 'orange', 'pink', 'gray', 'cyan']

for i in range(len(digits.data)):
  plt.text(digists_tsne[i,0], digists_tsne[i,1], str(digits.target[i]),
           color = colors[digits.target[i]],
           fontdict={'weight':'bold', 'size':9})

plt.xlabel('t-SNE feature 0')
plt.ylabel('t-SNE feature 1')
plt.show()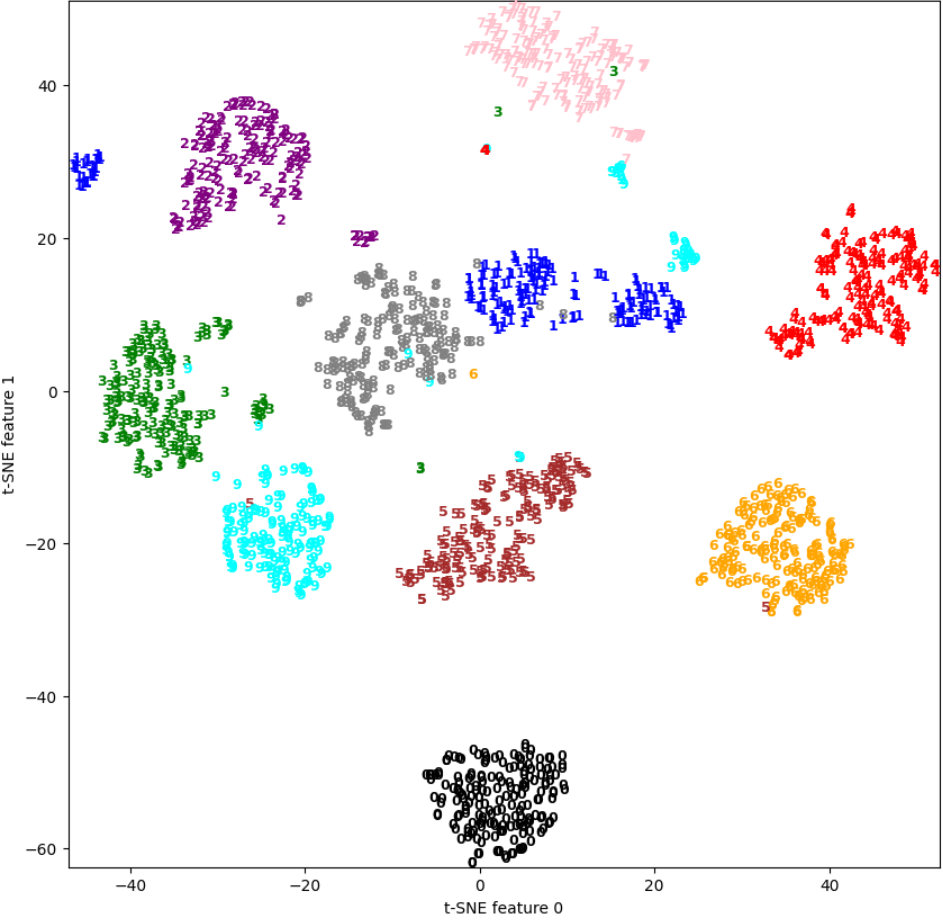

T-SNE Summary

• T-SNE는 차원 축소 및 시각화 도구로써 개발 (널리 사용됨)
• Perplexity 값에 따라 성능 차이 존재 (최적의 값을 위한 fine-tuning 필요)
• 시각화 기능만 존재(새로운 데이터를 받아 임베딩 불가)
• 데이터가 너무 클 경우, 학습에 시간 소요 많이 됨
  (해결책 : 여러 방법론 사용, PCA로 전처리 후 T-SNE 사용)