Big Data Analytics #05 Decision Tree

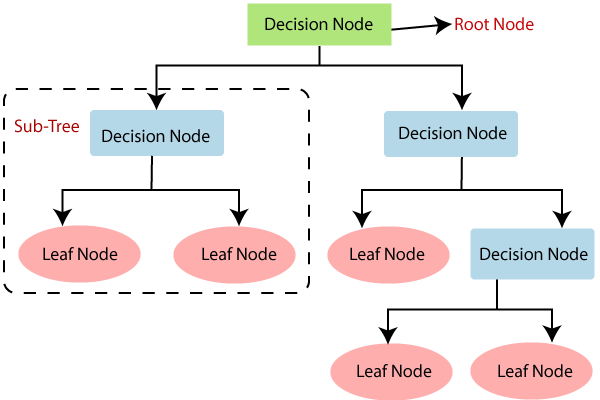
1. Decision Tree 개요

지도 학습 알고리즘 중 하나로 데이터의 특징과 레이블 간의 관계를 트리 구조로 표현하는 모델
(ex. 스무고개와 비슷한 방식으로 동작)

Decision Tree의 목적

• 예측 및 분류 : 주어진 입력 값에 대해 예측값을 생성하고 분류 수행
• 특징의 중요도 파악 :
  if-else 형태로 표현되며, 어떤 순서로 작용되고, 어떤 특징이 가장 분류에 중요한 영향을 미치는지 확인 가능
• Overfitting 방지 : 가지치기 기법을 사용하여 불필요한 가지를 제거

Decision Tree의 목표

여러 Decision Tree 중 어떤 모델이 좋은지 결정하는 것
(어떤 feature를 먼저 사용하느냐에 따라 여러 가지 Decision Tree 만들 수 있음)

-> 변별력이 좋은 질문을 던지는 것

2. ID3 (Iterative Dichotomiser 3)

: Decision Tree model

Entropy

어떤 확률 분포의 평균 정보량 or 무작위성(불확실성)의 정도를 나타냄

Impurity(불순도)

불순물이 포함된 정도, 데이터의 혼잡도를 나타내는 지표
(불순도가 적을 수록 좋은 질문)

-> Decision Tree는 불순도를 낮추는 방향으로 분기하는 model

ID3 Algorithm

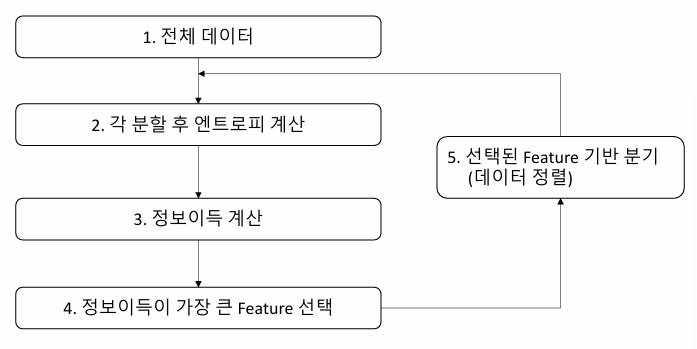
ID3 모델의 문제점

• 연속형 변수 처리 문제 : ID3 모델은 범주형 변수에 적합
• 다중 속성에 편향됨 : 속성의 값이 많을 수록 정보 이득에 유리함
• 다중 클래스 분리 어려움 : 클래수가 많아질 수록 정보 이득 차이가 작아지고, 불안정한 분할이 발생하기 쉬움
• 이상치에 민감 : 작은 노이즈도 분리 기준으로 삼아 트리 복잡해짐

3. C4.5 알고리즘

: Decision Tree model

ID3 학습의 개선된 버전으로, 기존 의사결정 트리의 한계를 극복하기 위해 설계되었음

C4.5의 개선점

• 정보 이득비
  : 기존 정보 이득 대신, 정보 이득비를 사용하여 속성 선택 편향을 줄이고, 더 정교한 불순도 측정 가능
• 다양한 변수 타입 지원
  : 범주형 변수 뿐만 아니라, 연속형 변수도 처리할 수 있어 실제 테이터 분석에 유연하게 적용 가능
• 결측치 처리
  : 불완전한 data set에도 적용 가능
• 가지치기
  : overfitting 방지를 위한 기능 제공

---

Information Gain Ratio (IGR)

Information Gain으로만 계산하면, 단순히 분할의 수가 많아져도 정보이득이 높다고 판단
분할의 수를 고려하기 위해 Information Gain Ratio(IGR)를 사용

Parent node $p$가 $k$개의 partition으로 나뉘어지고, $i$ 번째 partition의 크기를 $n_i$라 할 때

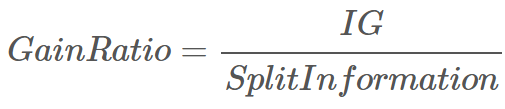
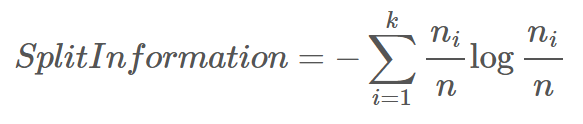
Split Information은 특정 지표로 분기했을 때, 생성되는 가지 수에 대한 Entropy 값

• $SplitInformation$이 커질 수록, 중요도 낮아짐

---

수치형 변수 처리

특정 임계값(threshold)을 정하면 수치형변수도 범주형변수처럼 사용 가능

임계값(Threshold)을 기준으로 이진 분할
분할 기준은 정보이득 or 정보이득비율 최대화 지점으로 정함

수치형 분할 기준

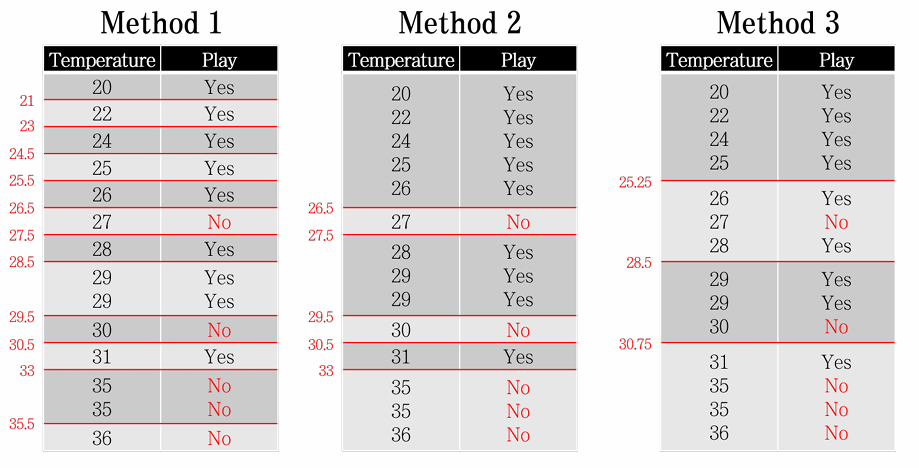
• Method 1. 값이 바뀌는 모든 지점
• Method 2. Output class가 바뀌는 지점
• Method 3. Q1, Median, Q3 지점

Step1. 수치형 속성의 값을 오름차순으로 정렬

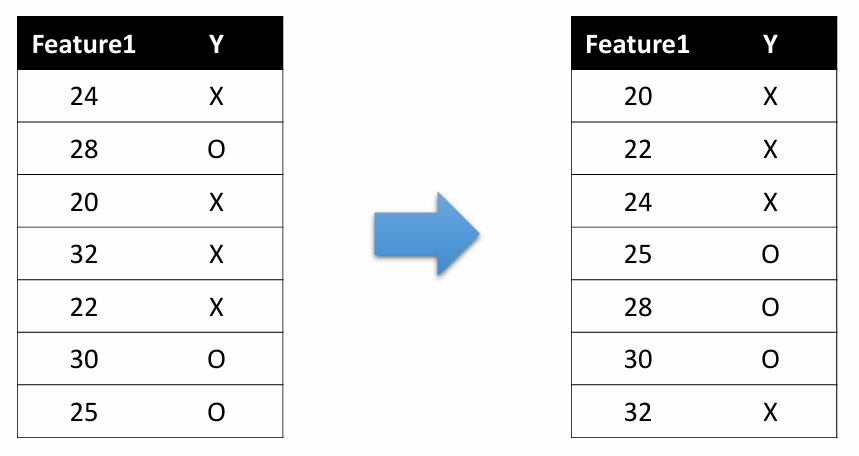
Step2. 수치형 변수를 나누는 기준에 따라 분할 후보 설정

기준: Output class가 바뀌는 지점 (문제에서 지정)

Step3. 각 임계값에 대해 데이터를 이진 분할

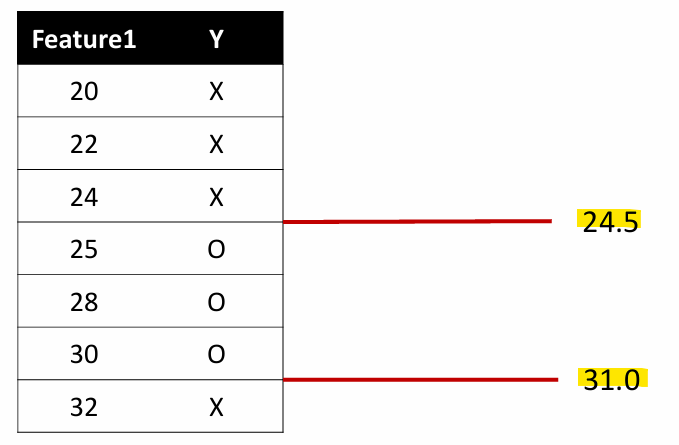
Step4. 각 분할의 정보이득 계산

Step5. 정보이득이 가장 큰 임계값을 선택

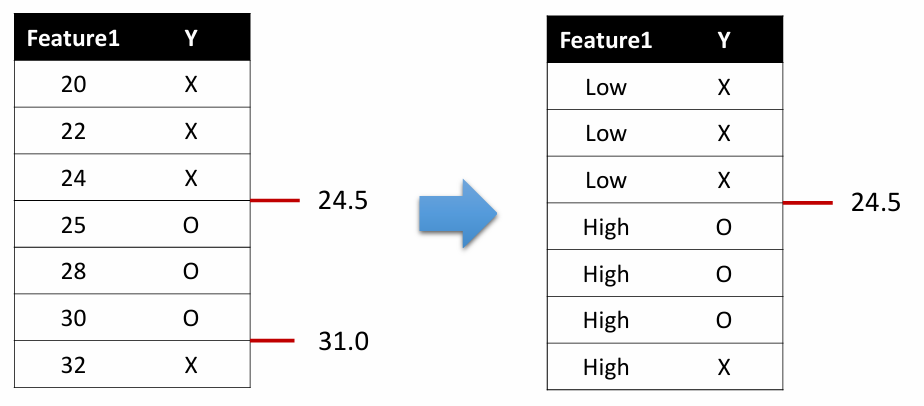
Threshold = 24.5 일 때 IG가 높으므로, 24.5를 선택

---

결측치 처리

C4.5는 결측지 처리에도 유연한 방법을 제공함 (아래 예제와 함께 방법 참고)

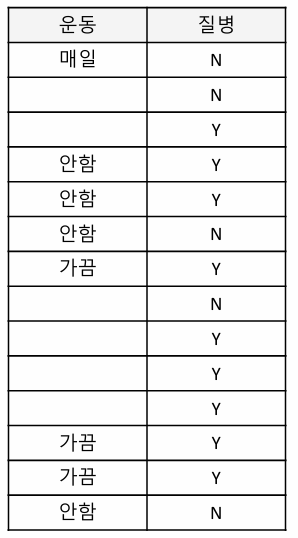
Step1. Entropy 계산시, non-missing value로만 계산

Step2. Information Gain을 Weighted IG로 변경

결측치가 있는 sample의 가중치 계산 및 적용

Step3. SplitInformation 계산 시 Missing value를 하나의 class로 보고 계산

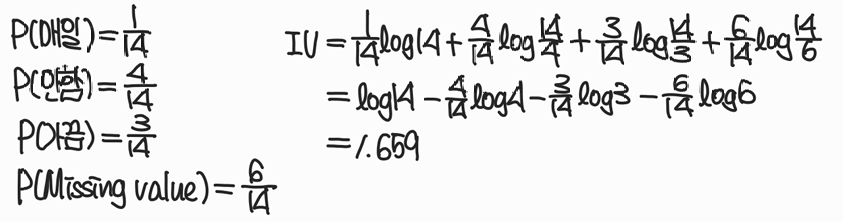
Step4. Information Gain Ratio 계산

4. Decision Tree Example

: ID3 model로 Play에 대한 Decision Tree 만들기

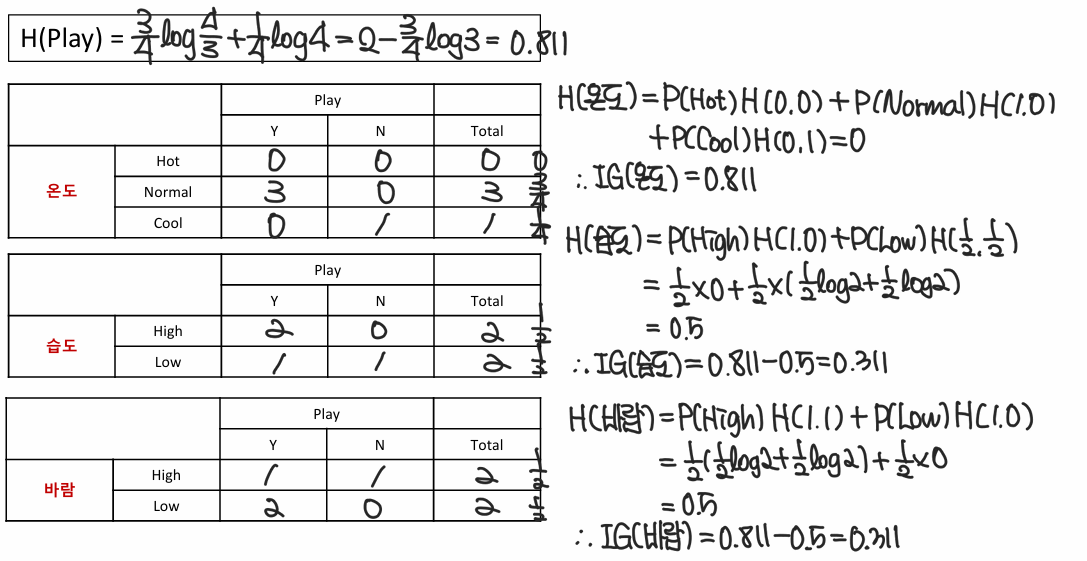
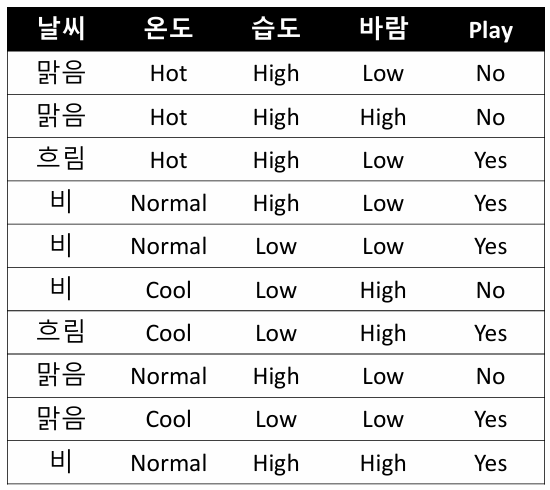
Step1. 전체 data 확인

label(play)에 대해 날씨, 온도, 습도, 바람과 관련된 표 작성할 준비하기

Step2. 각 분할에 대한 Entropy 계산

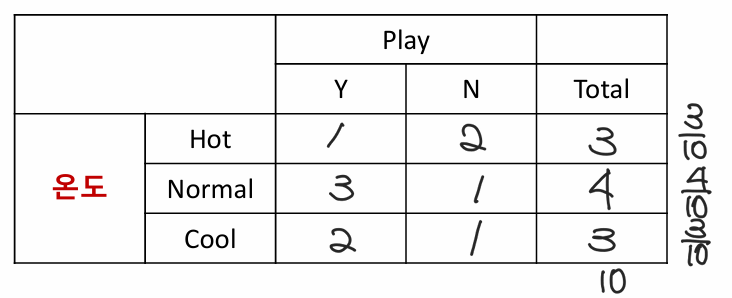
2-1. 온도에 대한 Entropy 계산

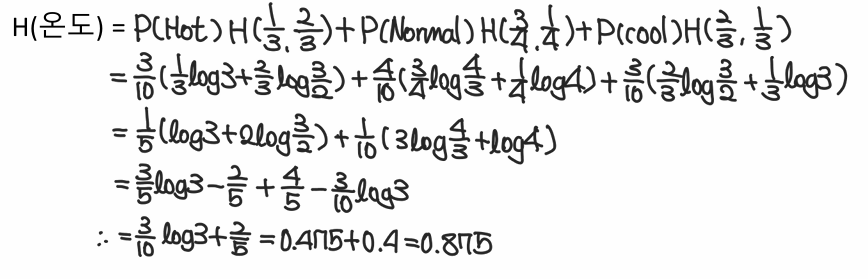
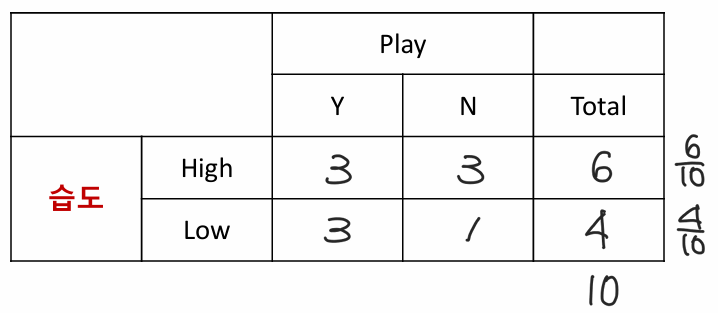
2-2. 습도에 대한 Entropy 계산

2-3. 바람에 대한 Entropy 계산

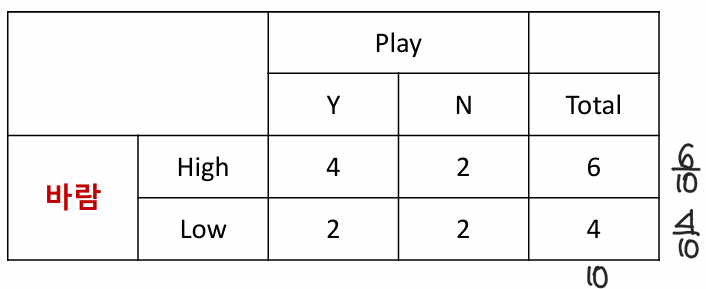
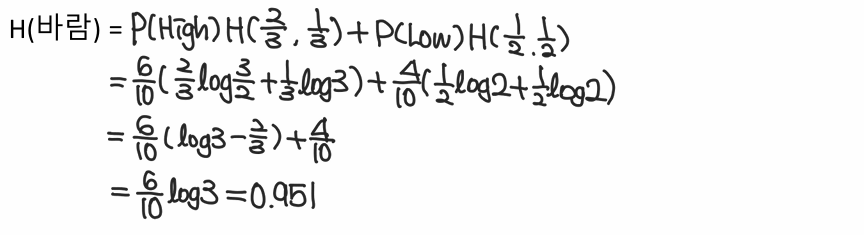
Step3. Information Gain(IG) 정보 이득 계산

3.1 $H(부모)$ 에 대한 Entropy 계산

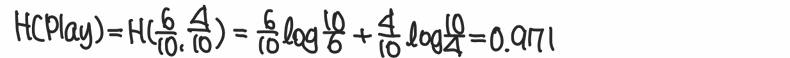
3.2 Information Gain(IG) 계산

Step4. 정보이득이 큰 feature 선택

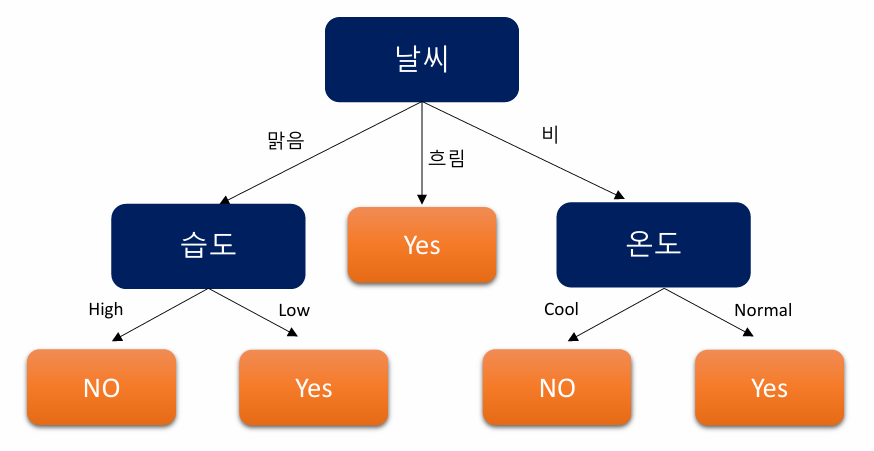
날씨에 대한 IG가 가장 크기에 다음 분기는 날씨를 토대로 진행

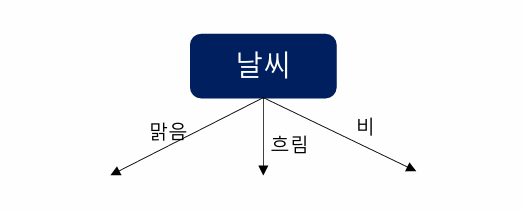
Step5. 선택된 feature에 따라 분기 후 알고리즘 반복

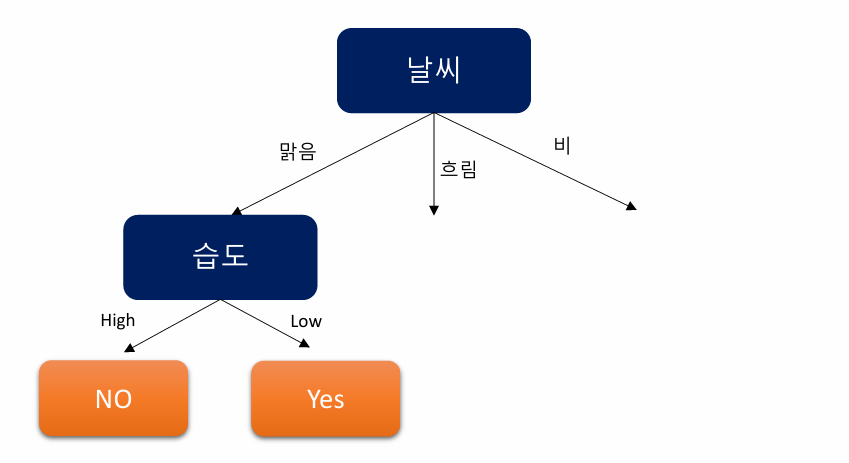
5-1. 날씨-맑음 Branch에 대해 Decision Tree 알고리즘

IG가 가장 큰 습도 feature 선택 후 분기

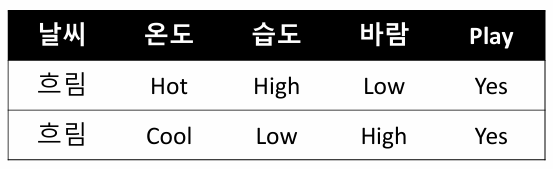
5-2. 날씨-흐림 Branch에 대해 Decision Tree 알고리즘

무조건 label이 Yes로 나오니 IG 계산 할 필요 없음

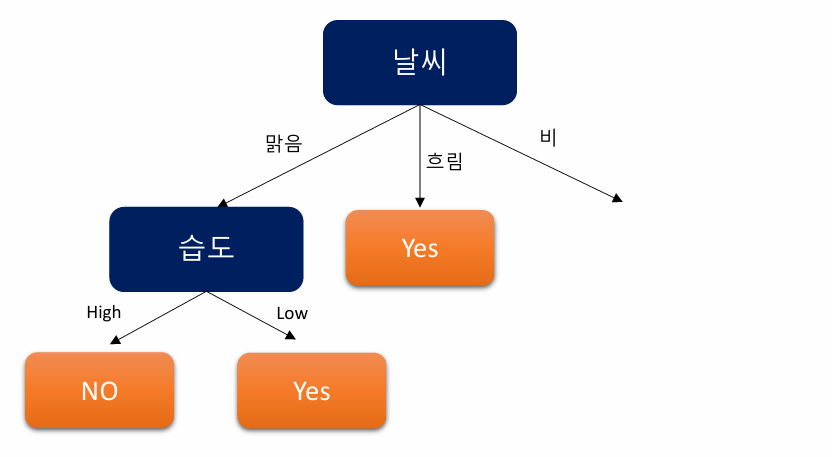
5-3. 날씨-비 Branch에 대해 Decision Tree 알고리즘

IG가 가장 큰 온도 feature 선택 후 분기