A Search는 그래프 탐색 알고리즘 중 하나로, 최단 경로 문제와 같은 최적화 문제를 푸는 데 사용된다. A Search는 목표에서 가장 가까운 상태를 탐색하는 방식으로 동작한다.
A Search의 핵심 아이디어는 이미 비용이 높은 경로를 확장하는 것을 피하는 것이다. 이를 위해 각 상태에 대해 종합 비용인 f(n)* 을 계산하고, 이 비용을 기반으로 확장 순서를 결정한다.
A Search에서 사용되는 평가 함수f(n) 은 상태 n 에 대한 경로의 종합 비용을 나타낸다. 이 종합 비용은 실제 경로 비용인 g(n) 과 휴리스틱 함수로 나타낸 예상 비용인 h(n) 을 합친 값이다.
f(n) = g(n) + h(n)
- g(n) = 시작 상태에서 상태 n 까지의 경로 비용
- h(n) = 상태 n 에서 목표까지의 예상 비용
- f(n) = 상태 n을 통과하는 경로의 총합 비용A Search에서 사용되는 휴리스틱 함수는 "안정된(Admissible)" 휴리스틱 함수여야 한다. 이것은 휴리스틱 함수가 실제 최적 비용 h(n) 을 과소평가하지 않아야 한다는 것을 의미한다. 즉, h(n) <= h*(n), when h*(n) is true cost from n 이고, 또한 h(n)* 은 항상 0 이상이어야 한다.
특징
- 목표 지향적 (Goal-Directed)
- A* Search는 목표에서 가장 가까운 상태를 탐색하는 방식으로 동작한다.
- 휴리스틱 함수(Heuristif Function)
- A Search는 휴리스틱 함수 h(n) 를 사용하여 각 상태 n* 에서 목표까지의 추정 비용을 계산한다.
- 이 휴리스틱 함수는 가능한 한 정확한 목표까지의 비용 예측을 제공해야 한다.
- 비용 함수(Cost Function)
- A Search는 각 상태까지의 경로 비용 g(n)* 을 추적한다.
- 이 비용은 시작 상태에서 현재 상태까지의 경로 비용을 나타낸다.
- 평가 함수 (Evaluation Function)
- A Search는 평가 함수 f(n) = g(n) + h(n)* 를 사용하여 각 상태의 "종합 비용"을 계산한다.
- 이 종합 비용은 목표까지의 경로 비용과 휴리스틱 예측을 합친 값이다.
- 탐욕스러운 선택 (Greedy Choice)
- A Search는 각 단계에서 f(n)* 이 가장 작은 상태를 선택하여 확장한다.
- 이 선택은 "탐욕스러운" 결정으로, 종합 비용이 가장 작은 상태를 우선적으로 확장하는 것을 의미한다.
- 최적성(Optimality) 보장
- A* Search는 [[Heuristic (휴리스틱)#Admissible Heuristics (안정된 휴리스틱)|"안정된(Admissible)" 휴리스틱]] 함수를 사용할 경우 최적성(Optimality)을 보장한다.
안정된 휴리스틱 (Admissible Heuristir)의 조건
1. 가능성 조건 (Consistency Condition)
모든 상태 n에 대해 휴리스틱 함수 h(n)는 목표까지의 실제 최적 비용인 h*(n)을 과소평가하지 않아야 한다.
즉, h(n) <= h*(n) 이어야 한다.
2. 비음수 조건 (Non-Negativity Condition)
휴리스틱 함수 h(n)은 항상 0 이상이어야 한다.
즉 h(n) >= 0 이어야 한다.- 안정된 휴리스틱은 휴리스틱 함수가 실제 최적 비용을 과소평가하지 않고 항상 0 이상이기 때문에 A* Search가 최단 경로를 찾을 수 있다.
- A* Search는 최적해를 찾을 수 있는 알고리즘이다. 즉, 최단 경로를 찾는데 사용된다.
- A Search는 f(n) 값이 C*(최적해 의 비용) 보다 작은 모든 노드를 확장하고, f(n) 값이 C 와 같은 노드 중 일부만 확장한다. 그러나 f(n) 값이 C* 보다 큰 노드는 확장하지 않는다.

- 완전성(Completeness) 보장
- A* Search는 목표 상태가 도달 가능한 한, 그래프 내의 모든 가능한 경로를 탐색하며 최적해를 찾을 수 있다.
- 다만, 무한히 많은 f(n) 값이 f(G) 보다 작은 노드가 있는 경우 제외된다.
- 시간 복잡도 (Time Complexity)
- A* Search의 실행 시간은 휴리스틱 함수의 상대 오차와 최적 경로의 길이에 지수적으로 영향을 받는다.
- 휴리스틱 함수의 품질과 최적 경로가 얼마나 복잡한지에 따라 실행 시간이 결정된다.
- 공간 복잡도 (Space Compolexity)
- A* Search는 모든 확장된 노드를 메모리에 유지한다.
- 이것은 메모리 사용량이 큰 단점으로 작용할 수 있으며, 메모리 사용량이 문제가 될 수 있다.
증명
A* Search가 최적 경로를 보장하는 이유는 다음과 같다.
- A Search에서 최적해가 아닌 서브 옵티멀한(SubOptimal) 목표 상태 G2* 가 생성되고 큐(Queue)에 있는 상황을 가정한다.
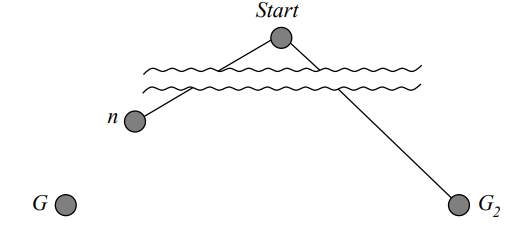
- 노드 n 은 확장되지 않은 노드(UnExpanded Node)로 최적 경로에서 최적 목표 G1 까지 가는 최단 경로 상에 있다.
- 이제 최적 목표 G1 과 서브 옵티멀(SubOptimal) 목표 G2 의 f(n) 값 및 g(n) 값에 대한 비교를 수행한다.
- f(G2) = g(G2) 이며,이는 G2가 서브옵티멀하기 때문에 최적 비용 경로의 일부가 아니라는 것을 의미한다.
- g(G1) 은 최적 목표 G1 까지의 실제 비용을 나타내며, G2가 서브 옵티멀하기 때문에 g(G2) > g(G1) 이다.
- h(n) 은 휴리스틱 함수로서, "안정된(Admissible)" 휴리스틱 함수이므로, h(n)은 G1 까지의 최단 경로 추정 비용을 나타낸다. 따라서 h(G2) >= h(n) 이 성립한다.
- f(n)은 평가 함수로서 f(n) = g(n) + h(n) 이므로, f(G2) = g(g2) + h(g2), f(n) = g(n) + h(n)이다. 따라서 f(g2) > f(n) 이다.- f(G2) > f(n) 이므로 A Search는 항상 f(n) 값이 더 낮은 노드 n 을 먼저 확장하고, f(G2) 값이 더 높은 목표 G2 를 확장하지 않는다. 이로 인해 A Search는 최적 목표 G1에 도달하는 최단 경로를 찾아낸다.
Lemma (보조정리)
A Search는 노드의 f(n) 값이 작은 노드를 먼저 확장한다.
A Search는 Search를 컨투어를 순차적으로 추가하면서 노드를 확장한다.
- f-contour
- 동일한 f(n) 값을 가지는 모든 노드의 모음
- f-contours 는 f(n) 값이 커질수록 컨투어 번호가 증가한다.
- f-contours 는 너비 우선 탐색(BFS)의 레이어(layer)와 유사한 개념이다.
컨투어 i 에 속한 모든 노드는 동일한 f 값 f(i) 을 가지며, f(i) 는 컨투어 i+1 에 속한 노드의 f 값 보다 작다.
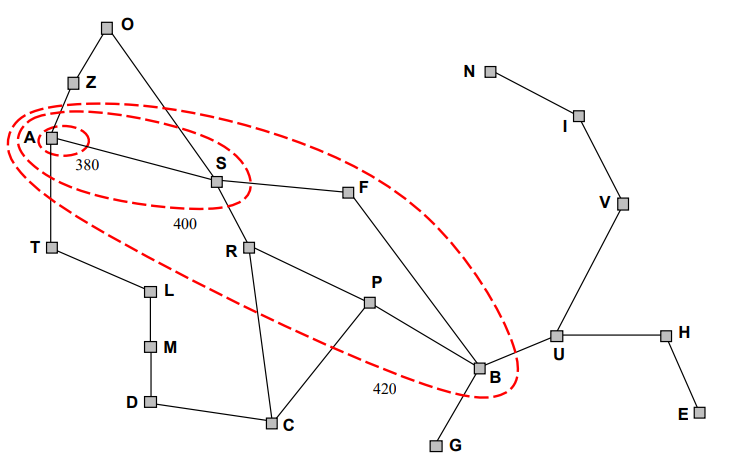
이러한 방식으로 A Search는 노드를 f 값이 낮은 순서대로 확장하여 최적 경로에 빠르게 수렴하고, 불필요한 노드 확장을 피한다. 따라서 A Search는 최적 경로를 효과적으로 찾는 데 사용되며, 휴리스틱 함수가 안정(Admissible)된 조건을 충족할 때에만 이러한 특성이 보장된다.
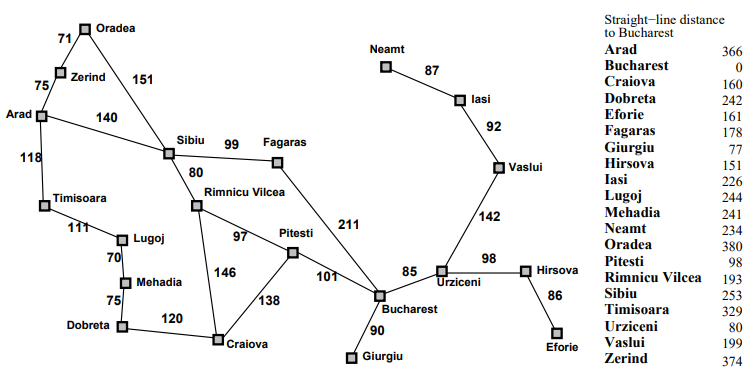
Example: Romania
- 다음과 같은 지도가 있을 때 Arad에서 출발하여 Bucharest 까지의 최단 경로를 구하는 문제이다.
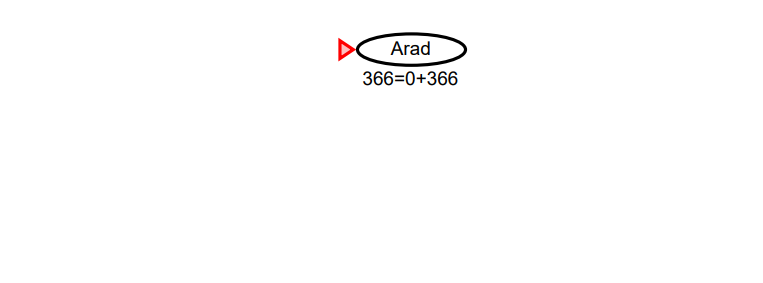
- Step 1.
-
Arad에서 Bucharest까지의 최단 경로를 구하는 문제이므로 휴리스틱 함수 hSLD(n) = 각 n에서 Bucharest 까지의 직선거리 를 사용한다.
-
비용 함수 g(n) = 경로 비용 이므로 아직 어떤 경로도 경유하지 않았기 때문에 g(n) = 0 이다.
-
휴리스틱 함수 h(n) = 현 노드에서 목표 노드까지의 직선 거리 이므로 h(n) = 366 이다.
-
따라서 평가 함수 f(n) = g(n) + h(n) 이므로 f(n) = 0 + 366 = 366 이다.
-
Step 2.

-
Arad의 자식 노드인 [Sibiu, Timisoara, Zerind] 를 추가한다.
-
각 노드에서 평가 함수 f(n) 을 구한다.
-
이 때 비용 함수 g(n) 은 출발 지점에서 각 노드 까지 경유한 비용이다. 따라서 Sibiu는 Arad에서 출발하여 도로를 경유한 비용인 140 이 g(n) 이다.
-
각 노드 별 h(n) 은 현 노드에서 목표 노드 Bucharest 까지의 직선 거리이므로 Sibiu는 253 이 된다.
-
추가 노드: [Sibiu: 393 = 140 + 253, Timisoara: 447 = 118 + 329, Zerind: 449 = 75 + 374]
-
노드 리스트: [Sibiu: 393, Timisoara: 447, Zerind: 449]
-
경유 노드: [Arad]
-
노드 리스트 중 평가 함수의 값이 가장 작은 [Sibiu: 393 = 140 + 253]으로 확장한다.
-
현재 노드가 Bucharest 인지 검사한다.
-
Step 3.
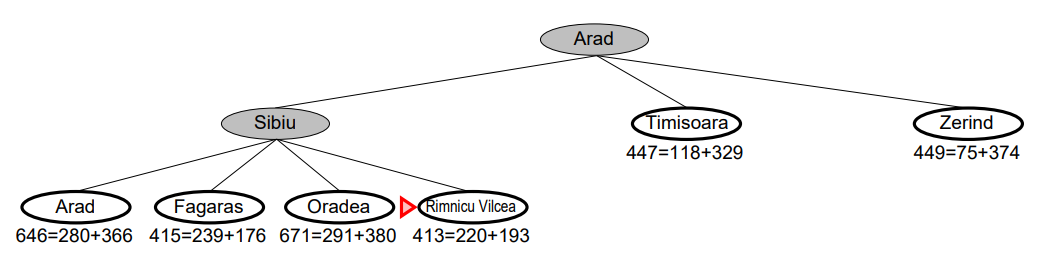
-
Sibiu의 자식 노드인 [Arad, Fagaras, Oradea, Rimnicu Vilcea]를 추가한다.
-
각 노드에서 평가 함수를 적용하여 계산한다.
-
추가 노드: [Arad: 646 = (140 + 140) + 366, Fagaras: 415 = (140 + 99) + 176, Oradea: 671 = (140 + 151) + 380, Rimnicu Vilcea: 413 = (140 + 80) + 193]
-
노드 리스트: [Fagaras: 415, Oradea: 671, Rimnicu Vilcea: 413]
-
경유 노드: [Arad, Sibiu]
-
노드 리스트 중 평가 함수의 값이 가장 작은 [Rimnicu Vilcea: 176]으로 확장한다.
-
현재 노드가 Bucharest 인지 검사한다.
-
Step 4.
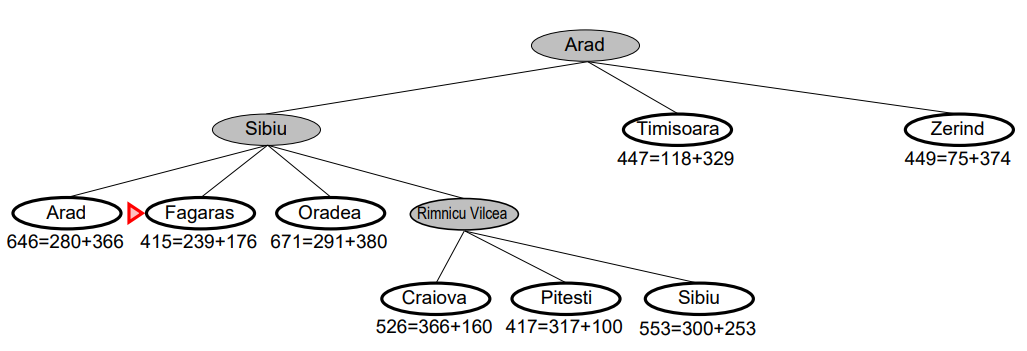
-
Rimnicu Vilcea의 자식 노드인 [Craiova, Pitesti, Sibiu] 를 추가한다.
-
각 노드에서 평가 함수를 적용하여 계산한다.
-
추가 노드: [Craiova: 526 = (140 + 80 + 146) + 160, Pitesti: 417 = (140 + 80 + 97) + 100, Sibiu: 550 = (140 + 80 + 80) + 253]
-
노드 리스트: [Fagaras: 415, Oradea: 671, Rimnicu Vilcea: 413, Craiova: 526, Pitesti: 417]
-
경유 노드: [Arad, Sibiu, Rimnicu Vilcea]
-
노드 리스트 중 평가 함수의 값이 가장 작은 [Fagaras: 415] 로 확장한다.
-
현재 노드가 Bucharest 인지 검사한다.
-
Step 5.
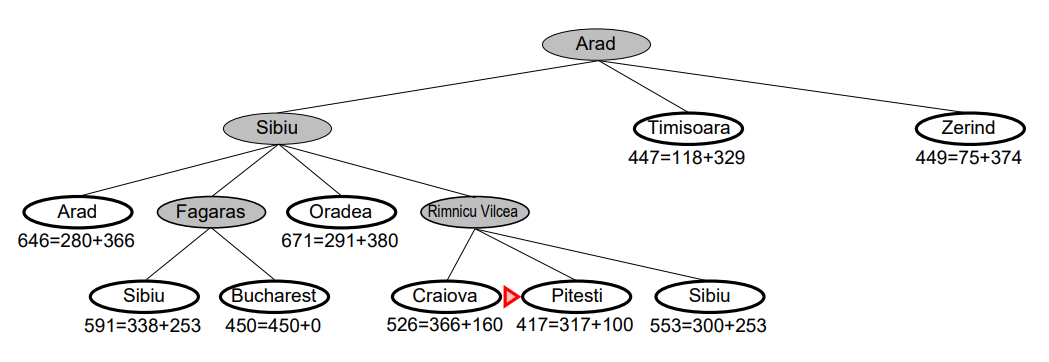
-
Fagaras의 자식 노드인 [Sibiu, Bucharest]를 추가한다.
-
각 노드에서 평가 함수를 적용하여 계산한다.
-
추가 노드: [Sibiu: 591 = (140 + 99 + 99) + 253, Bucharest: 450 = (140 + 99 + 211) + 0]
-
노드 리스트: [Oradea: 671, Craiova: 526, Pitesti: 417, Bucharest: 450]
-
경유 노드: [Arad, Sibiu, Fagaras]
-
노드 리스트 중 평가 함수의 값이 가장 작은 [Pitesti: 417] 로 확장한다.
-
현재 노드가 Bucharest 인지 검사한다.
-
Step 6.
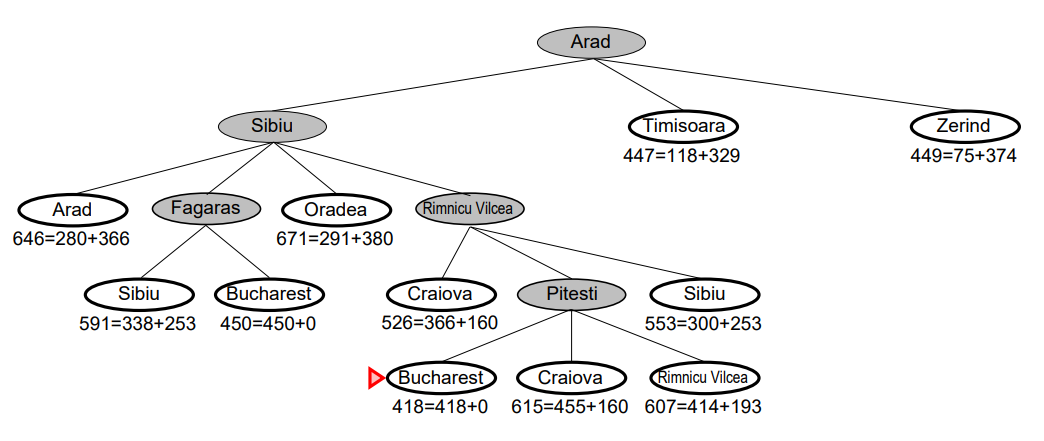
- Pitesti의 자식 노드인 [Bucharest, Craiova, Rimnicu Vilcea] 를 추가한다.
- 각 노드에서 평가 함수를 적용하여 계산한다.
- 추가 노드: [Bucharest: 418 = (140 + 80 + 97 + 101) + 0, Craiova: 615 = (140 + 80 + 97 + 138) + 160, Rimnicu Vilcea: 607 = (140 + 80 + 97 + 97) + 193]
- 노드 리스트: [Oradea: 671, Craiova: 526, Bucharest: 418]
- 경유 노드: [Arad, Sibiu, Rimnicu Vilcea, Pitesti]
- 노드 리스트 중 평가 함수의 값이 가장 작은 [Bucharest: 418] 로 확장한다.
- 현재 노드가 Bucharest 인지 검사한다.
- 현재 노드가 Bucharest 이므로 A* Search를 종료한다.
