Informed Search (정보를 활용한 탐색, 혹은 Heuristic Search)는 목표를 향해 효과적으로 탐색하기 위해 추가적인 정보나 휴리스틱(heuristic)을 활용하여 탐색을 더 효율적으로 수행하는 알고리즘이다. 이 알고리즘은 목표에 도달하기 위한 가능한 경로를 판단하고 가장 유망한 경로를 먼저 탐색하려는 데 주로 사용된다.
UnInformed Search (무지한 탐색)에서는 전체 상태를 경험적으로 분석할 수 없기에 Goal State로 향하는 어떠한 방향성을 가지고 있지 않고 모든 방향으로 뻗어나간다. Informed Search는 이러한 단점을 극복하기 위해 휴리스틱을 적용하여 단점을 극복하였다.
Informed Search Algorithms은 최적화 문제, 게임 트리 탐색, 머신 러닝, 로봇 경로 계획, 자연어 처리 등 다양한 분야에서 활용된다. 특히 휴리스틱을 통해 추가 정보를 활용하므로 효율적인 경로 탐색 및 문제 해결을 위한 강력한 도구로 활용된다.
Heuristic (휴리스틱)
- Heuristic (휴리스틱)은 결정 문제나 최적화 문제의 해결에 사용되는 규칙 또는 방법으로, 일반적으로 문제의 복잡성을 감소시키기 위해 사용된다.
Best-First Search (최선 우선 탐색)
- Best-First Search (최선 우선 탐색)은 Informed Search 알고리즘 중 하나로, 휴리스틱 함수를 사용하여 상태 공간을 탐색하는 방법이다.
Greedy Search (탐욕 알고리즘)
- Greedy Search (탐욕 알고리즘)은 탐색 알고리즘의 하나로, 각 단계에서 가장 "탐용스러운" 선택을 통해 상태 공간을 탐색하는 방법이다.
A* Search
- A* Search는 그래프 탐색 알고리즘 중 하나로, 최단 경로 문제와 같은 최적화 문제를 푸는 데 사용되는 효율적인 방법 중 하나 이다.
Relaxed Problems
Traveling Salesperson Problem (여행하는 외판원 문제, TSP)
- TSP는 모든 도시를 한 번씩 방문하면서 최단 경로로 여행하는 문제이다. 이 문제는 결정론적 특성과 어려운 조건으로 알려져 있으며, 완전한 해결이 어려운 문제 중 하나 이다.
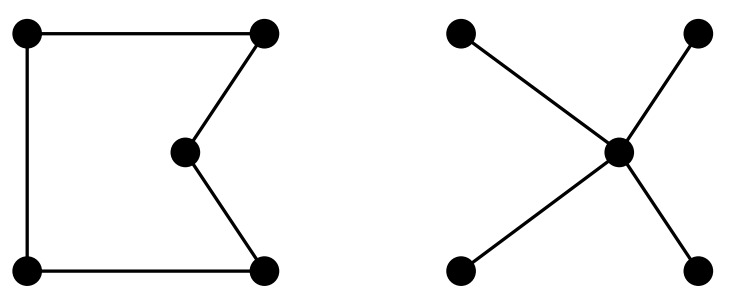
Minimum Spanning Tree (최소 신장 트리, MST)
- 최소 신장 트리는 그래프의 모든 노드를 연결하면서 가장 적은 비요을 가지는 서브 그래프이다. 이것은 여행하는 외판원 문제의 최적 해결책의 하한 경계를 제공하는 중요한 정보이다.
- 이 최소 신장 트리는 O(n^2) 시간 안에 계산할 수 있으며, 최단 경로로 여행하는 데 필요한 최소 비용 이상을 제공한다.
- 따라서 TSP 문제의 최적 해결책은 최소 신장 트리의 비용보다 항상 더 크게 된다.
