3D Rotation About Arbitrary Axis

임의의 축을 중심으로 3차원 공간에서 물체를 회전시키는 방법은 다음과 같다.

회전축이 좌표축 $(x, y, z)$ 과 정렬되지 않은 경우, 이를 구현하기 위해서는 좌표계를 회전축과 정렬시키고 나서 회전한 후, 다시 원래 좌표계로 복원하는 과정이 필요하다.

1. 임의 축 정의

임의의 축을 벡터 $u=(u_x, u_y, u_z)$로 정의한다. 이 벡터는 회전축으로 $u$ 벡터를 중심으로 물체를 회전 시킬 것이다.

2. 회전 변환 과정

임의의 축 $u$ 를 기준으로 회전시키기 위해서는 좌표계를 변환한 후 회전하는 방법을 사용한다. 회전 과정은 아래와 같이 3단계로 이루어진다.

1. 좌표계 정렬
   회전축이 $z$축(혹은 $x, y$축)에 평행하도록 좌표계를 변환(회전) 한다.
2. 회전 적용
   $z$축을 기준으로 회전 행렬을 사용하여 물체를 회전 시킨다.
3. 좌표계 복원
   처음에 정렬했던 좌표계를 다시 원래 상태로 되돌린다.
   $u=(x, y, z)$
   Rotate $u$ onto the z-axis

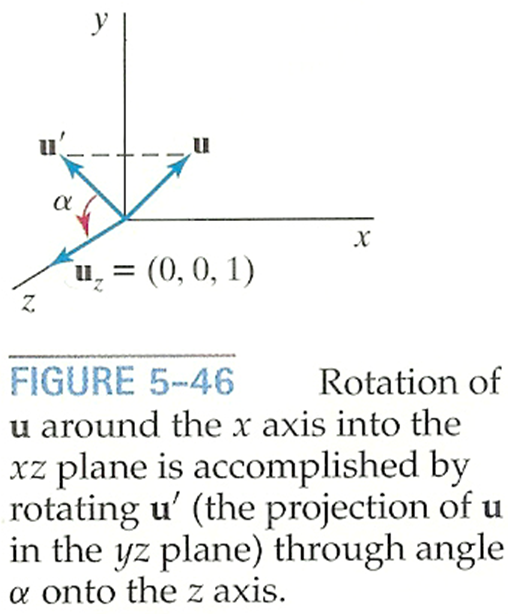
• $u^\prime$: Project $u$ onto yz-plane to compute angle $\alpha$

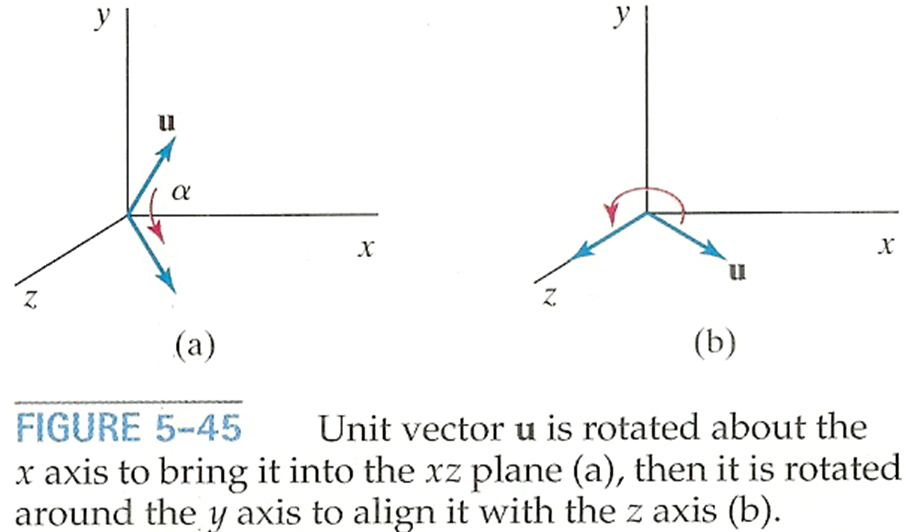
• • $u^{\prime\prime}$: Rotate $u$ about the x-axis by angle $\alpha$

• Rotate $u^{\prime\prime}$ onto the z-axis

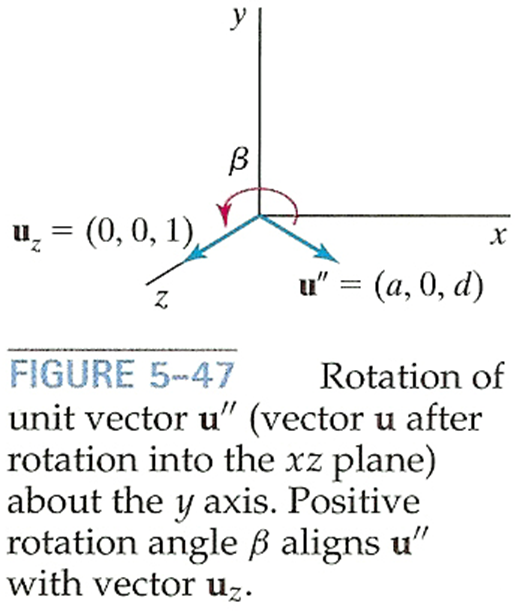
Example

임의의 축 $u$ 벡터가 다음과 같이 있다고 하자.
$u=(a, b, c)$

$u$ 벡터를 yz 평면에 사영한 $u^\prime$ 벡터는 다음과 같다.

$u^\prime=(0, b, c)$

그리고 최종적으로 만들 z 축 벡터 $u_z$ 는 다음과 같이 정의된다.

$u_z=(0, 0, 1)$

우리는 $u^\prime$ 에 회전 행렬을 적용하여 $u_z$ 벡터로 만들 것이다. 이를 위한 회전 행렬(x-rotation)은 다음과 같이 정의된다.

여기서 $\cos{\alpha}$와 $\sin{\alpha}$는 각각 dot product 와 cross product를 이용해 구할 수 있다.

이를 정리한 회전 행렬 $R_x(\alpha)$ 는 다음과 같다.

혹은 각도 $\alpha$ 를 다음과 같이 계산하여 구할 수 있다.