Eular Angle

Eular Angle (오일러 각)은 3차원 공간에서 물체의 회전 방향을 표현하는 방법 중 하나이다. 오일러 각은 물체가 각각의 좌표 축($x, y, z$)에 대해 순차적으로 회전하는 각도를 의미하며, 회전을 표현하기 위해 3개의 각도가 사용된다. 이를 통해 물체의 방향을 이해하거나 제어할 수 있다.

구성

Eular Angle 은 세 개의 축을 중심으로 한 회전으로 설명되며, 각 축에 대한 회전 각도를 차례로 적용한다.

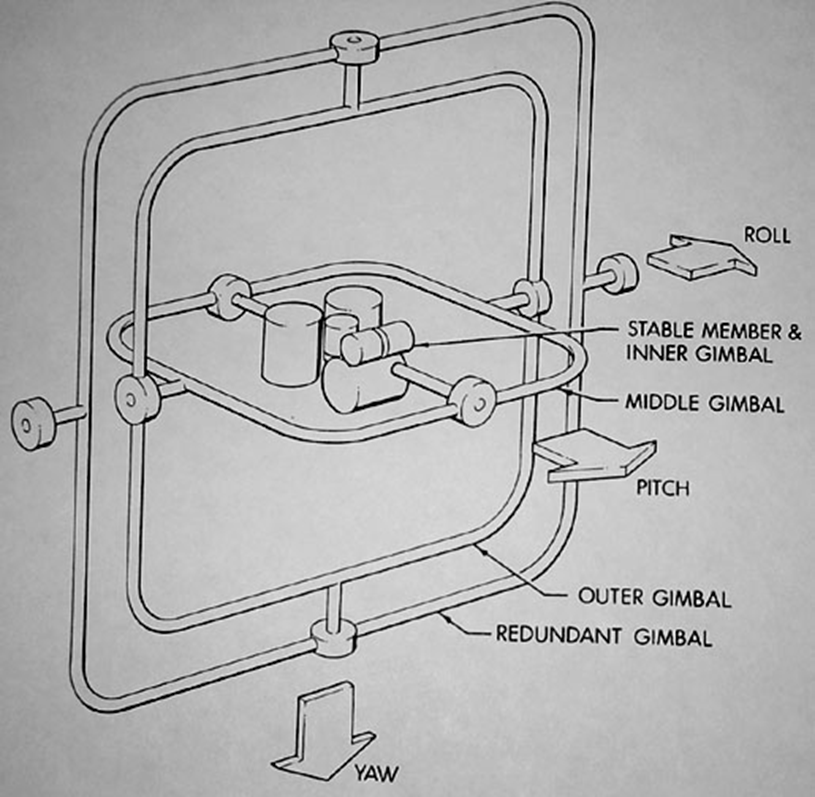
1. Pitch
   x축을 기준으로 하는 회전으로 물체를 위아래로 기울이는 동작과 같다.
2. Yaw
   y축을 기준으로 하는 회전으로 물체를 좌우로 회전시키는 동작과 같다.
3. Roll
   z축을 기준으로 하는 회전으로 물체를 좌우로 비트는 동작과 같다.

Eular Angle은 다음의 12개의 조합으로 표현할 수 있다. 일반적으로는 XYZ 혹은 ZYX를 많이 사용한다.

• XYZ, XYX, XZY, XZX
• YZX, YZY, YXZ, YXY
• ZXY, ZXZ, ZYX, ZYZ

XYZ 의 조합으로 나타낸 Eular Angle은 다음의 행렬$R_{XYZ}(\gamma, \beta, \alpha)$ 로 나타낼 수 있다.

Example: Gimbal

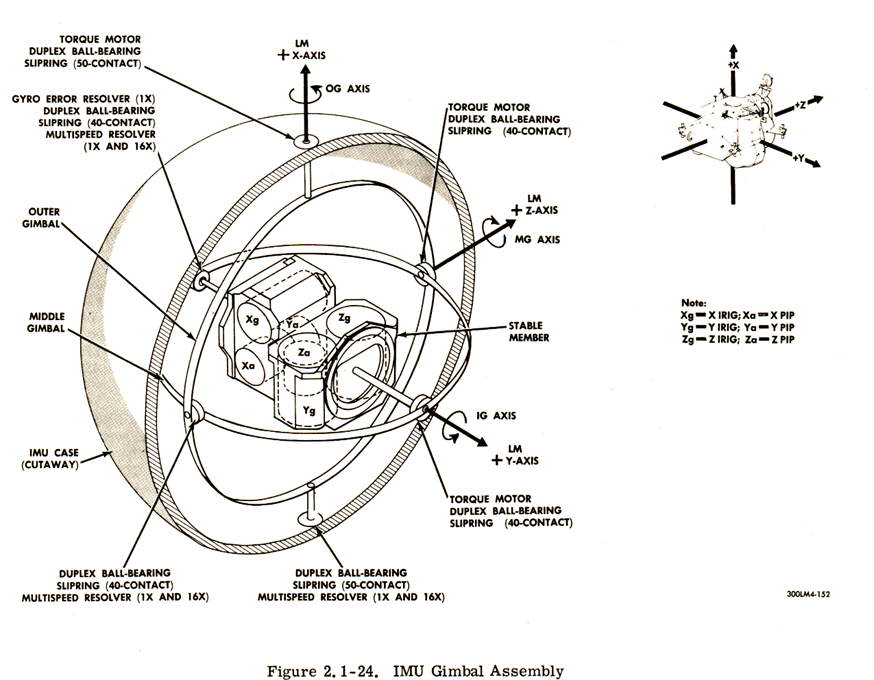
장점

Eular Angle은 물체의 회전 방향을 각 축에 대해 명확하게 설명할 수 있기 때문에 직관적이다. 또한 각 축에 대한 회전 변환을 행렬로 표현하기 쉽다.

단점

Eular Angle은 한 각을 표현할 때 여러 행렬로 동시에 표현 가능하기 때문에 굉장히 모호하다. 이로 인해 물체의 부드러운 움직임을 표현하는데 매우 제한적이다. 이 문제를 해결하기 Eular Angle로 해결하기 위해서는 회전 행렬의 순서를 조합하여 표현하는 방법이 있을 수 있다. 그러나 이 방법은 각 프레임마다 회전 행렬을 구하고 행렬의 곱을 계산해야 하기 때문에 비효율적이다.

또한 Eular Angle은 Gimbal Lock 현상이 발생한다.

Gimbal Lock (짐벌 락)

Gimbal Lock은 회전 축 중 하나가 다른 축과 정렬될 때 발생하는 현상으로, 회전 축이 두 개로 줄어들어 더 이상 원하는 방향으로 회전할 수 없게 되는 문제(회전 자유도가 줄어드는 현상)이다. 예를 들어, pitch 축을 90도로 회전 시키면 yaw와 roll축이 서로 겹치게 되어 자유롭게 회전할 수 없게 된다.

이로 인해 특정 각도에서 회전이 제한되고, 원하는 회전 방향으로 객체를 제어할 수 없게 된다.

이러한 문제를 해결하기 위해 Quaternions 을 사용할 수 있다.