[컴퓨터그래픽스] Geometric Objects and Its representations
Scalars
- Scalars α,β,γ from a scalar field
- Operations α+β, α⋅β , 0, 1, −α, ()−1
Vectors
- Vectors u,v,w from a vector space
- Vector addition u+v, subtraction u−v
- Zero vector 0
- Scalar multiplication αv
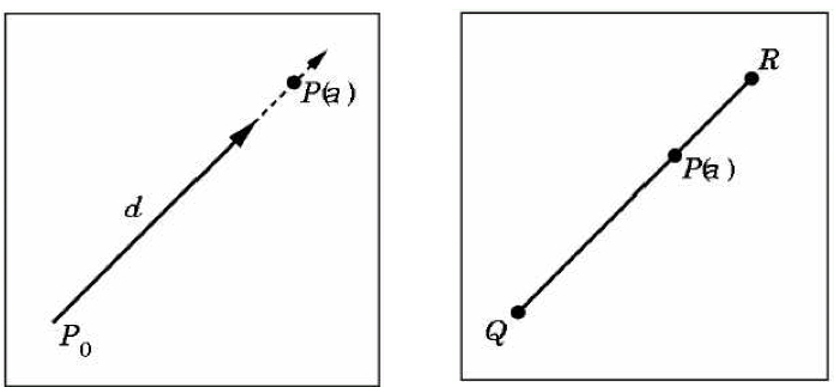
Lines and line Segments
- Parametric form of line: P(α)=P0+αd
- Line segment between Q and R: P(α)=(1−α)Q+αR for0≤α≤1
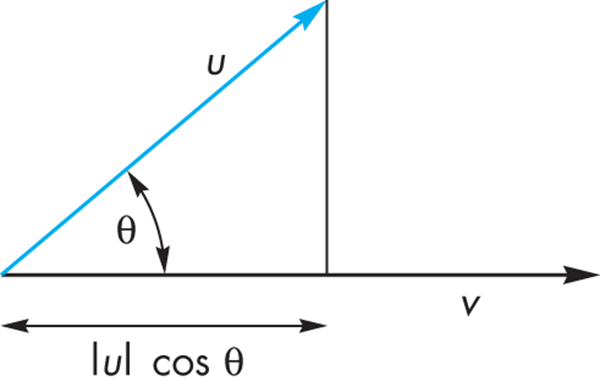
Dot Product (Projection)
- Dot Product projects one vector onto another vector
- u⋅v=u1v1+u2v2+u3v3=∣u∣∣v∣cos(θ)
- prvu=(u⋅v)v/∣v∣2
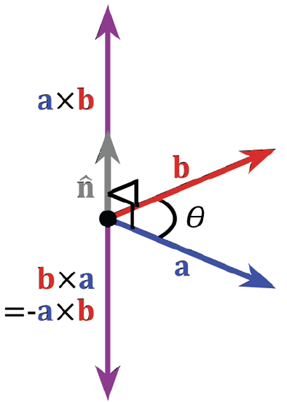
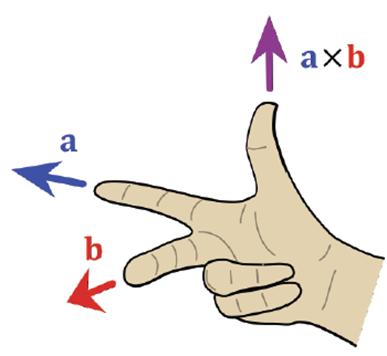
Cross Product
- ∣a×b∣=∣a∣∣b∣∣sin(θ)∣
⎝⎜⎛a1a2a3⎠⎟⎞×⎝⎜⎛b1b2b3⎠⎟⎞=⎝⎜⎛a2b3−a3b2a3b1−a1b3a1b2−a2b1⎠⎟⎞
- Cross product is perpendicular to both a and b
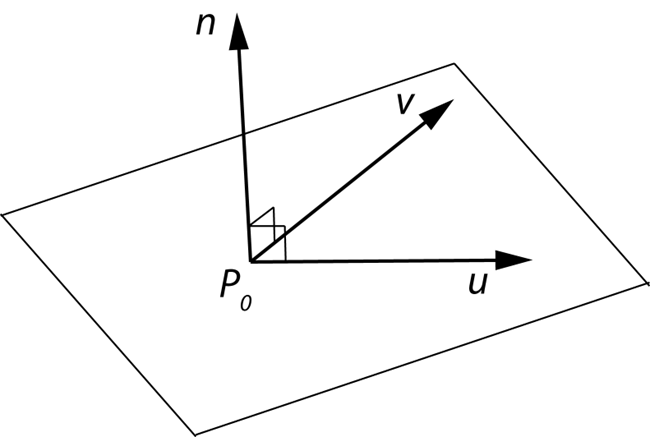
Planes
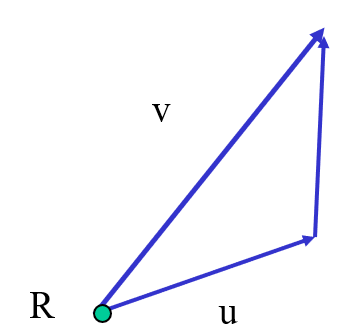
- A Plane can be defined by a point and two vectors or by three points
- P(α,β)=R+αu+βv
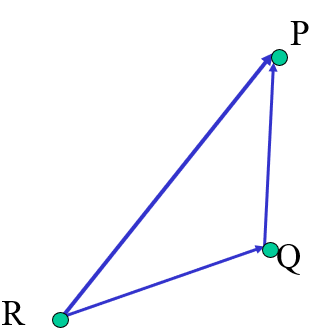
- P(α,β)=R+α(Q−R)+β(P−Q)
Planes and normal
- Plane defined by Point P0 and vectors u and v
- u and v should not be parallel
- Parametric form: T(α,β)=P0+αu+βv (α and β are scalars)
- n=u×v/∣u×v∣ is the normal
- n⋅(P−P0)=0 if and only if P lies in plane