개요
선형회귀방식으로 머신러닝을 진행할 때, 모델 평가를 할 때 평가 지표로 MSE(Mean Square Error)를 사용한다.
캐글에서 자전거 수요 예측 데이터분석을 할 때, 캐글의 평가지표는 RMSLE(Root Mean Square Log Error)를 이용하는데 그 이유가 무엇인지에 대해 서술하고자 한다.
이번 게시글은 내가 공부하는 책인 파이썬 머신러닝 완벽 가이드의 저자이신 박철민님이 인프런 강의에서 질문을 받고 답해주신 것을 내 나름대로 정리한 게시글임을 먼저 알린다. (https://www.inflearn.com/questions/22448)
본문
실습에서도 확인할 수 있다시피 RMSLE의 값과 RMSE의 값이 확연히 많이 차이나는 것을 볼 수 있다.
RMSLE: 1.165, RMSE: 140.900, MAE: 105.924왜 이런 결과값이 나오는 걸까?🤔
실습에서도 실제 값과 예측 값을 비교하는 부분이 있는데, 그 출력을 아래에 기재하도록 하겠다.
real_count predicted_count diff
1618 890 322.0 568.0
3151 798 241.0 557.0
966 884 327.0 557.0
412 745 194.0 551.0
2817 856 310.0 546.0위의 데이터프레임 칼럼은 오류 값이 가장 큰 순으로 5개만 정리한 것이다.
예측 오류가 높은 상위 데이터를 조사해 본 결과 타겟값이 큰 데이터들에 대해서 예측 오류가 잘못 나오면서 전체 데이터의 RMSE가 매우 커지게 되었다는 것을 의미한다.
비교적 정확한 예측 성능을 가진 모델이더라도, 타겟값이 작은 데이터에서 예측 오류가 나는 것 보다 타겟값이 큰 데이터에서 예측 오류가 나게 되면 그 임팩트가 더 크다는 것이다. 따라서 RMSE값이 비교적 큰 값으로 나오게 되는 것이다.
더욱이 이 캐글에서 진행할 수 있는 자전거 모델은 높은 타겟값을 가진 일부 데이터에 대해서 예측 정확도가 좋지 않아서 매우 높은 예측 오류값을 가지게 되고, 이것이 전체 RMSE값을 상대적으로 높이게 된 것이다.
그래서 이를 상쇄하기 위해서 로그를 씌워 해결하는 것이다!
로그 변환의 이유
그럼 왜 이를 상쇄하기 위해서 굳이 로그를 사용하는가? 👉로그변환과 np.log()가 아닌 np.log1p()를 하는 이유
이 블로그에 아주 자세하게 설명이 되어있다.
요약하자면 로그함수의 특징 때문에 x값이 점점 커짐에 따라 로그함수의 기울기는 급격히 작아진다. 이는 곧 큰 x값들에 대해서는 y값이 크게 차이나지 않게 된다는 것이고 이에 따라서 넓은 범위를 가지는 x를 비교적 작은 y값의 구간 내에 모이게 하는 특징을 가진다. 따라서 데이터 분포에서 밀집되어 있는 부분은 퍼지게, 퍼져 있는 부분은 모아지게 만들 수 있다는 것!!
이런 특성 때문에 한 쪽으로 몰려있는 분포에 로그 변환을 취하게 되면 넓게 퍼질 수 있는 것이다.
실제로 자전거 수요예측에서 데이터프레임의 hist()를 이용해 자전거 대여 모델의 타겟값인 count칼럼의 값 분포를 확인해보자면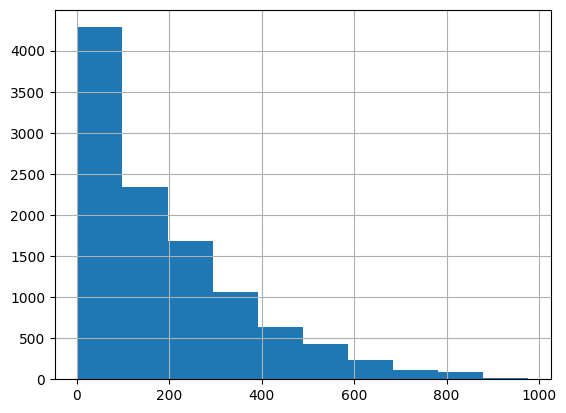
이와 같이 정규분포 형태가 아닌 0과 200사이에 왜곡돼 있는 것을 알 수 있다. 이렇게 왜곡된 값을 정규 분포 형태로 바꾸는 가장 일반적인 방법이 로그를 적용해서 변환하는 것이다.
타겟값에 로그를 취해 다시 히스토그램을 구해본다면
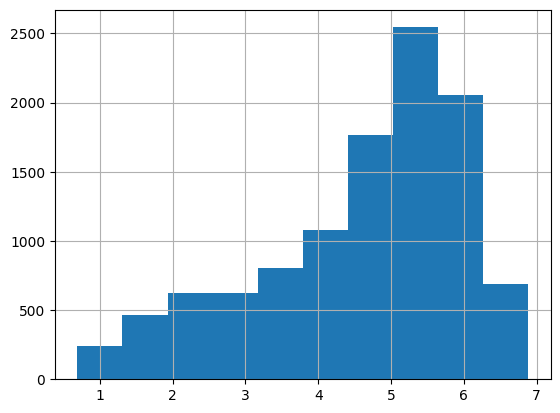
정규분포 형태는 아니지만 왜곡 정도가 많이 향상된 것을 확인할 수 있다.
RMSLE 구현하기
그렇다면 사이킷런에서 RMSLE를 구현하는 방법은 무엇일까?
안쉽게도 사이킷런은 RMSLE를 제공하지 않아서 RMSLE를 수행하는 성능 평가 함수를 직접 만들어서 사용해야 한다😂
사이킷런에 mean_squared_log_error()를 이용할 수도 있지만 데이터 값의 크기에 따라 오버플로/언더플로 오류가 발생할 수 있다고 한다.
from sklearn.metrics import mean_squared_error, mean_absolute_error
import numpy as np
def rmsle(y, pred):
log_y = np.log1p(y)
log_pred = np.log1p(pred)
squared_error = (log_y-log_pred)**2
rmsle = np.sqrt(np.mean(squared_error))
return rmsle
def rmse(y, pred):
return np.sqrt(mean_squared_error(y, pred))
def evaluate_regr(y, pred):
rmsle_val = rmsle(y, pred)
rmse_val = rmse(y, pred)
mae_val = mean_absolute_error(y, pred)
print('RMSLE: {0:.3f}, RMSE: {1:.3f}, MAE: {2:.3f}'.format(rmsle_val, rmse_val, mae_val))그렇다면 여기서 드는 의문점 한가지 더
왜 np.log()가 아니라 np.log1p()를 사용한 것일까?
np.log() vs np.log1p()
간단하게 말하자면 np.log()는 log(x)를 구하는 것이고 np.log1p()는 log(x+1)를 구하는 것이다.
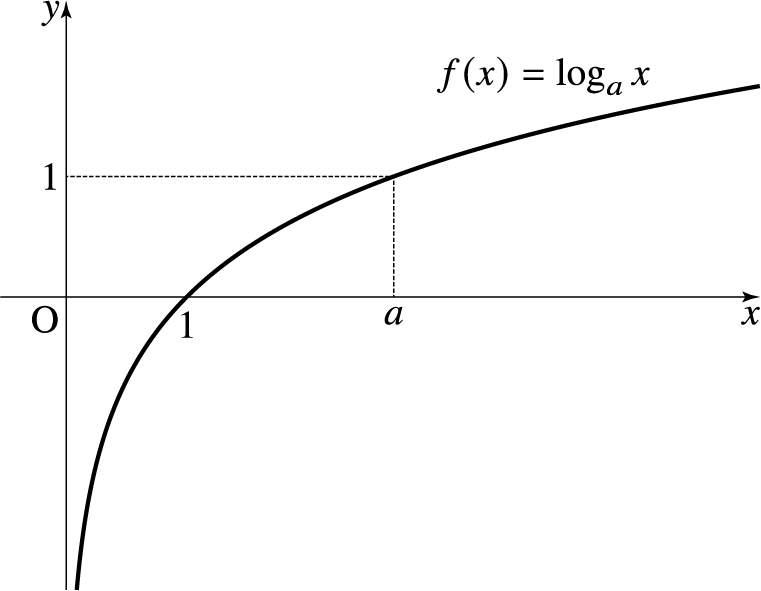
왜 +1을 해주냐면, 로그함수 그래프를 보면 알 수 있다시피 x가 0일 경우 y는 -inf값을 가지게 된다. 그래서 -inf값을 가지지 않도록 이를 방지해주는 것이 np.log1p()인 것이다.
자전거 수요 예측을 할 때 타겟 칼럼인 count를 log1p를 이용하여 로그 변환 후, 이를 반영해 학습/테스트 데이터 세트를 분할한 뒤 테스트 데이터 세트의 타겟값은 로그 변환 됐으므로 다시 expm1을 이용해 원래 스케일로 변환하고 예측값 역시 로그 변환된 타겟 기반으로 학습돼 예측됐으므로 다시 expm1으로 스케일을 변환하고 RMSLE를 확인하면 오류가 줄어든 것을 확인할 수 있다.
하지만 RMSE는 오히려 더 증가할 것이다. 이는 나머지 피처들을 원-핫 인코딩을 진행한 뒤 학습을 진행하면 된다.
나머지 과정은 나의 깃허브에 올려두었다. 👉[Github] Kaggle Bike Sharing Demand
