[타이타닉 생존자 예측 및 인사이트 도출 분석] - Random Forest 모델

저번 포스팅에서 했던 타이타닉 생존자 예측 및 인사이트 도출 분석을 이어서 ~ 이번엔 랜덤 포레스트(Random Forest) 모델을 사용해보겠댜 ! ⸜( •ᴗ• )⸝*

먼저 사용할 RandomForestClassifier 모듈을 임포트 한다.

from sklearn.ensemble import RandomForestClassifier

저번 로지스틱 회귀 모델 때와 같이 범주형 변수 인코딩과 입력데이터(X)와 예측값 y를 정의해준다. 그리고 데이터를 훈련용과 테스트용으로 나누어준다.

df = pd.read_csv('train.csv') 

# 범주형 변수 인코딩 (문자 -> 숫자)
df['Sex'] = LabelEncoder().fit_transform(df['Sex'])  # female=0, male=1
df['Embarked'] = LabelEncoder().fit_transform(df['Embarked'])

# df[['Pclass', 'Sex', 'Age', 'Fare', 'Embarked']].isnull().sum() 으로 결측치가 있는 지 확인 
df['Age'] = df['Age'].fillna(df['Age'].mean())  # 해결 -> 평균/최빈값으로 채우기

# 2. 사용할 변수(피처)와 예측할 대상(타겟) 정의
X = df[['Pclass', 'Sex', 'Age', 'Fare', 'Embarked']]  # 예측에 사용할 입력 데이터
y = df['Survived']                                    # 정답 (0 or 1)

# 3. 데이터 나누기 (훈련용과 테스트용으로)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

---

🌲 Random Forest 모델

랜덤 포레스트(Random Forest)란?
여러 개의 결정 트리(Decision Tree)를 만들고 그 결과를 앙상블(합침)하여 예측하는 모델

📈 랜덤 포레스트의 주요 특징

1. 앙상블 모델

하나의 모델이 아닌 여러 트리를 결합하여 예측

각각의 트리가 독립적으로 학습한 후, 다수결(분류) or 평균(회귀)으로 결과 결정

🎯 개별 트리보다 훨씬 안정적이고 성능 우수

2. 랜덤성 도입

데이터 샘플과 특성을 무작위로 선택하여 각 트리를 학습
→ Overfitting(과적합)을 방지하고 다양성 확보

두 가지 랜덤성:

• Bagging: 데이터 샘플을 랜덤하게 뽑아서 각 트리에 학습
• Feature Randomness: 트리 분기 시 사용할 특성 일부만 랜덤 선택

3. 과적합(Overfitting) 에 강함

단일 결정 트리는 과적합 위험이 큼 !
→ BUT 랜덤 포레스트는 "여러 트리 평균을 내므로 잡음(noise)에 덜 민감"하고, 높은 일반화 성능

📊 이때 과적합이란?
훈련 데이터에 너무 맞춰진(적합된) 모델
→ 마치 외운 것처럼 훈련 데이터만 잘 맞추고, 실제 문제(테스트 데이터)에는 일반화가 잘 안됨

📉 과적합 VS 과소적합 구분

구분	특징	예
과적합 (Overfitting)	훈련 데이터에는 성능 좋음, 테스트에는 나쁨	외운 학생
과소적합 (Underfitting)	"훈련 데이터조차" 잘 학습 못함	공부 안한 학생

4. 피처 중요도(Feature Importance) 제공

어떤 변수가 예측에 중요 한지를 알려줌
→ 예: 타이타닉 생존자 예측에서 Sex, Fare, Pclass 등이 중요할 수 있음!

5. 파라미터 조정 가능 (유연성)

조정 가능한 파라미터 많음 → "성능 튜닝 가능"

• n_estimators: 트리 개수
• max_depth: 트리 최대 깊이
• max_features: 분기 때 사용할 최대 변수 개수
• min_samples_split: 분기 최소 샘플 수
  → 과소적합/과적합 밸런스를 조절할 수 있음

---

랜덤 포레스트 모델을 정의해주고 학습시켜 예측을 수행하면 된다. 추가로 Test Accuracy 도 출력해보겠다.

rf = RandomForestClassifier(random_state=42)
rf.fit(X_train, y_train)

y_pred = rf.predict(X_test)
print("Test Accuracy:", rf.score(X_test, y_test))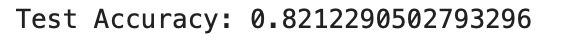

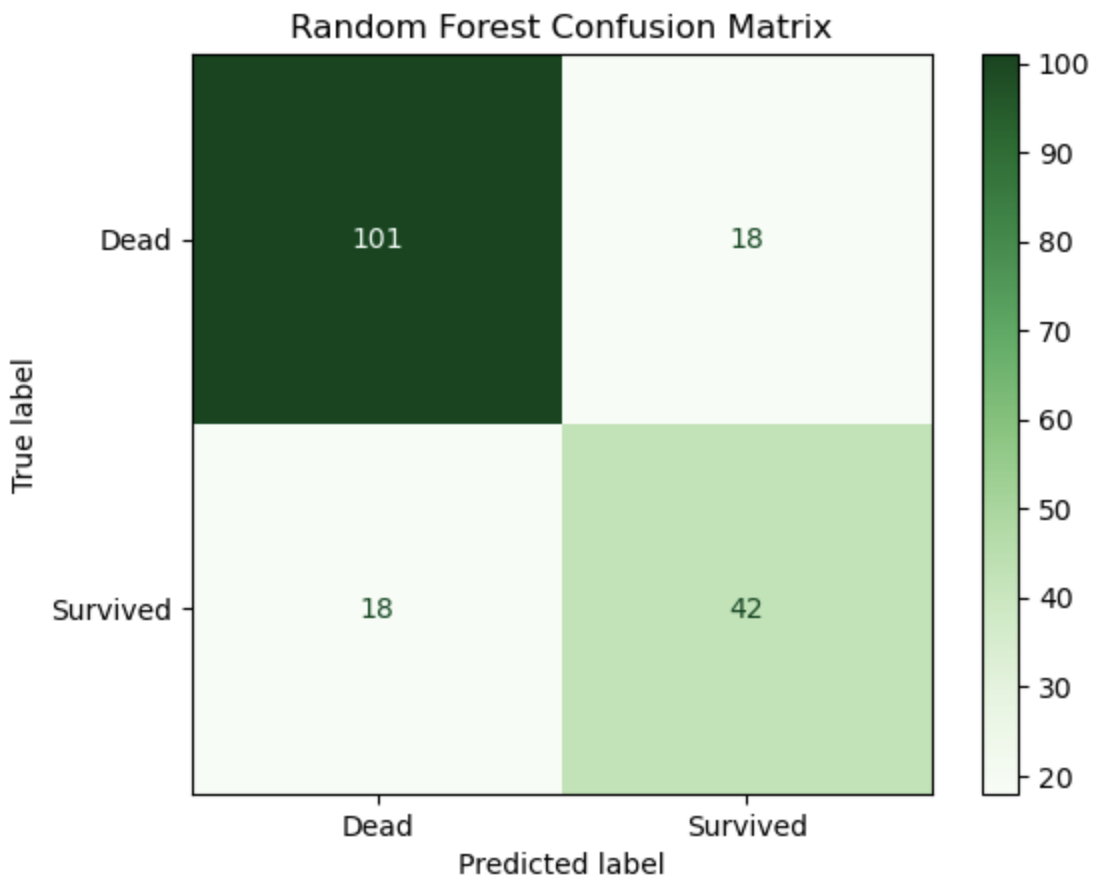
📊 confusion matrix 생성 후 시각화

cm = confusion_matrix(y_test, y_pred)
disp = ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=["Dead", "Survived"])
disp.plot(cmap='Greens', values_format='d')
plt.title("Random Forest Confusion Matrix")
plt.show()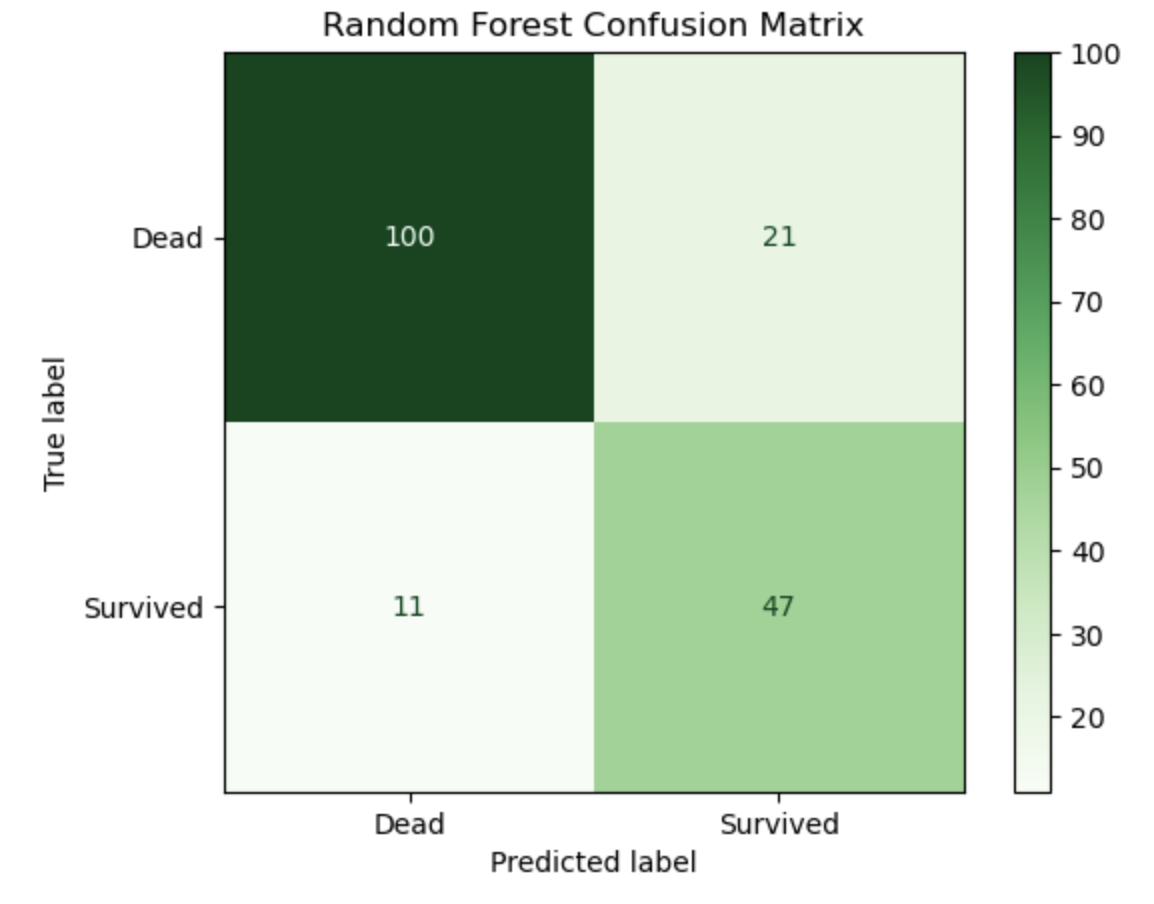

🔍 1. 모델 성능이 개선됐는가?

✔ Test Accuracy 증가 ❗️:

• 로지스틱 회귀: 72.6%
• 랜덤 포레스트: 82.1%

→ 약 2.2% 향상 → 전체적인 예측 정확도 향상!

🔍 2. 기존(로지스틱 회귀)보다 정확히 예측했는가?

• True Positive (생존 맞춤): 47 → 47

• True Negative (사망 맞춤): 90 → 100

---

• False Positive (살았다고 했는데 실제 사망): 26 → 21

• False Negative (죽었다고 했는데 실제 생존): 16 → 11

→ 모든 항목에서 오차가 줄었고, 정확히 맞춘 수가 늘었음
→ 예측 정확성 향상 !

🔍 3. 특히 생존자 예측률(재현율)이 좋아졌는가?

생존자 재현율 (Recall for Survived)

$Recall = \frac{TP}{TP+FN}$

• 로지스틱 회귀 :

  $\frac{47}{47+16}≈0.7460$

• 랜덤 포레스트 :

  $\frac{47}{47+11}≈0.8103$

  → ✔ 생존자 재현율이 약 7% 향상됨!

---

📑 feature importances 시각화

아까 얘기했던 랜덤포레스트의 특징 중 '피처 중요도(Feature Importance)'가 있었다.
추가로 이 중요도를 시각화 해보면 어떤 변수가 모델에서 중요하게 작용했는지를 알 수 있다.

먼저 시각화 모듈인 seaborn을 임포트 해준 다음,

import seaborn as sns

rf.feature_importances_ 로 피처 중요도를 가져온다. 그리고 feature_names는 변수들(Feature) 인 X 의 열로 한다.

importances = rf.feature_importances_
feature_names = X.columns

그리고 barplot 으로 시각화를 하면,

plt.figure(figsize=(8, 5))
sns.barplot(x=importances, y=feature_names)
plt.title("Feature Importance (Random Forest)")
plt.xlabel("Importance")
plt.ylabel("Feature")
plt.show()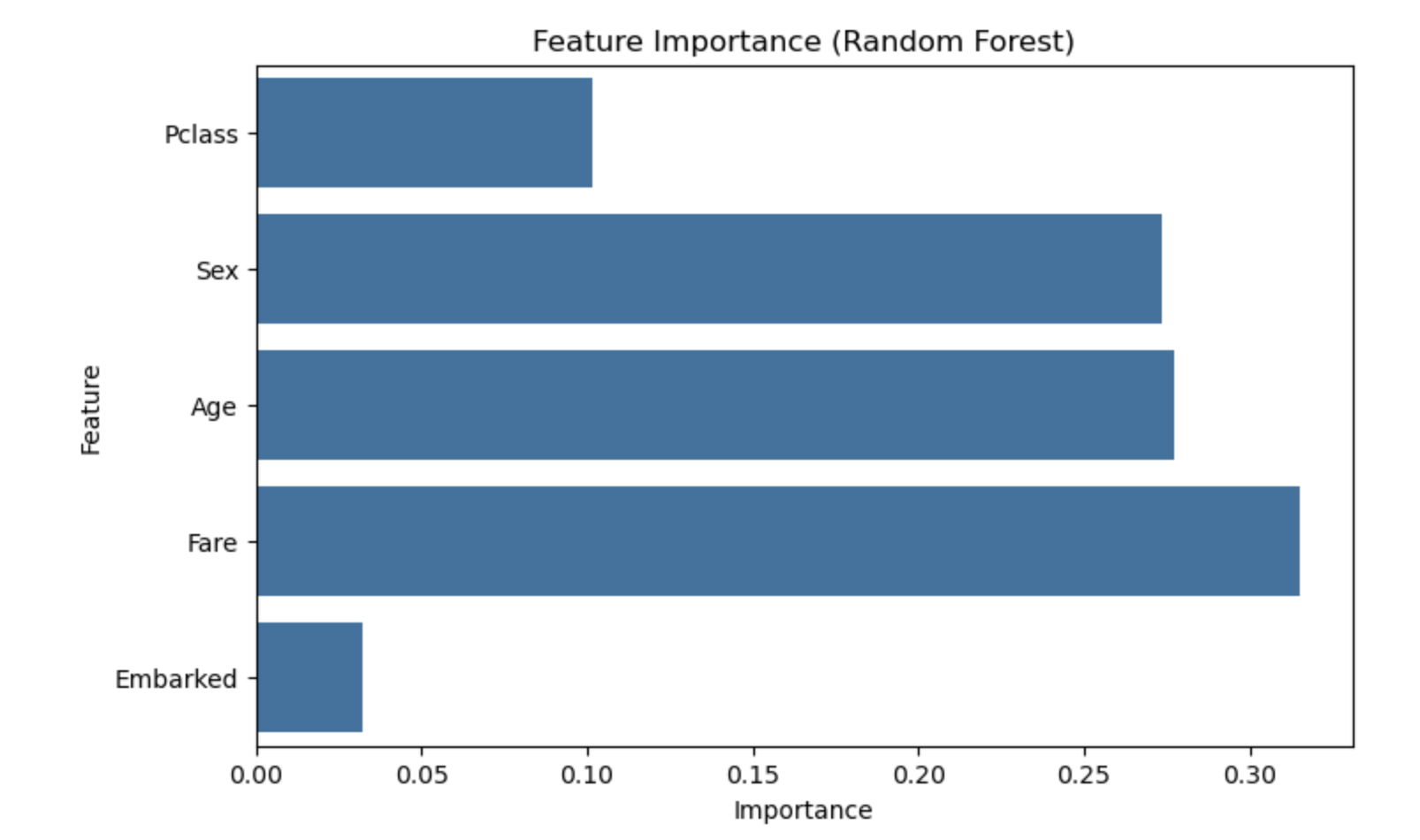

Feature	중요도 (대략)	해석
Fare	약 0.31	운임 요금은 생존 여부에 가장 큰 영향을 준다고 판단됨
Age	약 0.28	나이도 중요한 특성으로 작용함
Sex	약 0.27	성별 또한 생존 예측에 큰 기여
Pclass	약 0.10	객실 등급은 중간 정도의 영향
Embarked	약 0.03	탑승한 항구는 영향이 거의 없음

• 덜 중요한 피처(예: Embarked)는 제거하거나 단순화하여 모델을 더 간단하고 빠르게 만들 수 있고,
• 중요한 피처(예: Fare, Sex, Age)는 더 정교하게 다듬거나 파생변수를 추가해 예측력을 높일 수 있다.

라는 전략적 판단을 도출해낼 수 있다.
그럼 이 판단을 바탕으로 좀 더 예측력을 높이는 작업을 해보자 !

👍🏻 중요한 피처

1. Fare (운임)

# 로그 변환 (너무 큰 값 완화)
import numpy as np
X['Fare_log'] = np.log1p(X['Fare'])
# 구간화 (운임을 여러 등급으로 나눔)
X['Fare_bin'] = pd.qcut(X['Fare'], 4, labels=False)  # 4분위로 나눔

2. Age (나이)

# 결측치 채우기 (평균, 중간값, 그룹별 평균 등)
X['Age'] = X['Age'].fillna(X['Age'].median())
# 구간화
X['Age_bin'] = pd.cut(X['Age'], bins=[0, 12, 18, 35, 60, 100], labels=['Child', 'Teen', 'YoungAdult', 'Adult', 'Senior'])
# 파생 변수: 어린이 여부
X['IsChild'] = (X['Age'] <= 12).astype(int)

3. Sex (성별)

# 인코딩
X['Sex'] = X['Sex'].map({'male': 0, 'female': 1})
# 파생 변수: 여성 여부
X['IsWoman'] = (X['Sex'] == 1).astype(int)

👎🏻 덜 중요한 피처

1. Embarked (탑승구)

# Embarked 제거
X = X.drop('Embarked', axis=1)
# 모델에서 Embarked 변수를 제거해서 복잡도를 줄임.
# 변수의 중요도가 너무 낮아서 모델 예측에 거의 도움 안 됨.

# 또는 단순화
# 예: Embarked 값을 그룹화하거나 결측치를 하나의 그룹으로 처리
X['Embarked'] = X['Embarked'].fillna('Unknown')

이걸 바탕으로 다시 모델 훈련한다면 더 예측력을 높일 수 있을 것이다.

---

이렇게 랜덤 포레스트 모델 학습을 해보았고, 로지스틱 회귀 때와 어떤 점에서 달라졌는지 정확도, 혼동행렬, 재현율로 확인해 볼 수 있었다. 그리고 피처 중요도 시각화를 통해 어떤 피처가 더 중요한지 또한 잘 알고, 예측력을 높이도록 정교화하는 작업 또한 중요 하다는걸 알았다.
담 포스팅에는 하이라이트? 라고 할 수 있는 모델 성능 강화를 위한 파라미터 튜닝을 해 봄으로써..
" 더 정확하고 → 더 단순하고 → 더 빠른 모델 " 을 만들어 보고 싶다.

이상 두번째 포스팅을 마치겟댜 ! 🍀