
2년 전 방학 때 노트북과 핸드폰을 사기 위해..
나의 노동력을 갈아넣은 평택 삼성반도체 현장..
건물을 지어보자 뿌슝빠슝...🥵


문제 해석
무척이나 많은 변수를 입력받는 문제였다.
우선 T회의 테스트 케이스가 있고,
하나의 테스트 케이스 안에는 건물 수 N, 규칙 수 K가 있으며
각 건물이 지어지는 데 걸리는 시간 D, 그리고 건물의 건설 순서 X, Y가 주어진다.
마지막으로는 승리하기 위해 지어야 하는 건물 W를 입력 받는다.
이 때 우리가 구해야 할 것은 바로 건물 W까지 짓는 데 드는 최소 시간이다.
다음의 입력을 확인해보면,
1
8 8
10 20 1 5 8 7 1 43
1 2
1 3
2 4
2 5
3 6
5 7
6 7
7 8
7
하나의 테스트 케이스가 있고, 8개의 건물과 8개의 규칙이 존재한다.
각 건물을 짓는 데 걸리는 시간은 10, 20, ... 43 으로 주어졌고, 승리하기 위해 지을 건물은 7번이다.
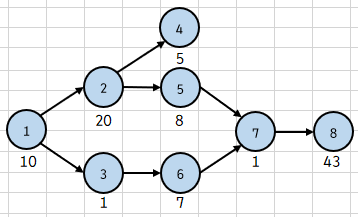
건물의 건설 순서까지 따지면 다음과 같은 구조로 이루어진다.
여기서 우리는 한번에 여러 건물을 동시에 지을 수 있고, 동시에 짓기 시작한 건물은 모든 건물이 건설되어야 다음 건물로 넘어갈 수 있다. 여기서 2, 3번 건물을 동시에 짓는다면, 3번 건물이 다 지어져서 6번 건물을 지으려 해도 2번 건물이 다 지어지기 전엔 6번을 지을 수 없게 된다.
따라서 7번 건물이 다 지어질 때 까지의 최소 시간은,
1(10) → 2,3(20) → 4,5,6(8) → 7(1) 의 순서로 지을 때 10+20+8+1=39 이다.
출력은 다음과 같다.
39
뭐가 필요할까
이 문제에서 필요한 것들은..
- 각 건물까지 짓는 데 최소 시간? BFS
- 그 최소 시간이 다음 건물의 최소 시간을 결정하는데 필요? DP
- 건물들 간의 짓는 순서를 알고리즘에 정확히 구현? 위상 정렬
여기서 위상 정렬이란 순서가 정해진 작업을 차례로 수행해야 할 때,
그 순서를 결정할 때 쓰이는 알고리즘이다. 나도 이번에 처음 알았당 🙃
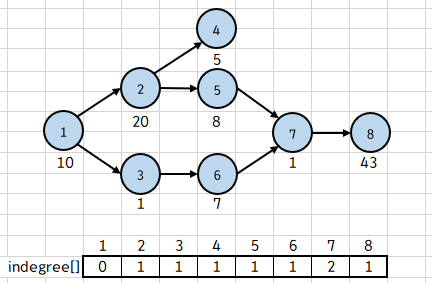
위상 정렬을 구현하기 위해 indegree[] 배열을 만든다.
이 배열에 들어가는 값은 해당 건물로 진입할 수 있는 건물의 수이며, 보통 진입차수 라고 한다.
이게 이 문제에서 어떻게 쓰이냐면, 우선 시작 건물을 정해야 BFS를 진행할 수 있으니
indegree[i] == 0;인 건물을 시작 건물로 정하여 큐에 삽입한다.
q.push(i);
dp[i] = D[i];dp[] 배열에는 i 건물까지 짓는 데 걸리는 시간을 저장하게 된다.
시작 건물이므로 i 건물까지 짓는데에는 해당 건물을 짓는 시간, D[i]가 저장된다.
그리고 시작된 BFS에서 큐의 top 원소를 현재 짓는 건물 curr에 저장하고, pop 한다.
int curr = q.front();
q.pop();지금 짓는 건물 curr과 그 다음에 지을 건물 next가 있을 때,
건물을 짓는 데 걸리는 시간에서 DP의 점화식이 쓰인다.
dp[next] = max(dp[next], dp[curr] + D[next]);건물을 지었다면 그 다음 건물을 큐에 삽입하게 되는데 이 조건이 다음과 같다.
--indegree[next] == 0즉, 지금 지은 curr에서 next가 유일한 다음 단계 건물이라면 큐에 삽입된다.
그래서 어떻게 했는데
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int T, N, K, W;
vector<int> D;
vector<vector<int>> v;
vector<int> dp; // dp[i]는 건물 i까지 짓기 위한 최소시간
vector<int> indegree;
void BFS();
int main() {
ios_base::sync_with_stdio(NULL);
cin.tie(NULL);
cout.tie(NULL);
cin >> T;
for (int i = 0; i < T; i++)
{
cin >> N >> K; // 건물 갯수 N, 연결수 K
D.resize(N + 1);
dp.resize(N + 1);
indegree.resize(N + 1);
v.resize(N + 1);
for (int j = 1; j <= N; j++)
{
cin >> D[j]; // 건설시간 D
}
for (int k = 1; k <= K; k++)
{
int x, y;
cin >> x >> y;
v[x].push_back(y); // 건물 연결상태 v (단방향)
indegree[y]++; // y 건물로 진입할 수 있는 건물수 (진입차수)
}
cin >> W;
BFS();
cout << dp[W] << "\n";
// 다음 T에 쓸 벡터 초기화
D.clear();
dp.clear();
indegree.clear();
v.clear();
}
return 0;
}우선 앞서 말한 변수와 벡터를 전역으로 선언한다.
또한 건물의 건설 규칙 x, y가 저장되는 벡터 v도 추가로 선언한다.
뒤에 설명할 BFS() 함수를 선언하고, main 함수를 작성하였다.
하나의 테스트 케이스에서 D, dp, indegree, v를 N+1 크기로 초기화한다.
N+1로 초기화 한 이유는 단순히 인덱스를 1부터 쓰기 위한 것이다.
이후 각 건물마다 걸리는 건설시간 D를 입력받고, 건물의 건설 순서 규칙도 입력받는다.
이 때, 그래프의 연결 상태를 입력할 때와 마찬가지로 v[x].push_back(y); 로 넣어준다.
y 건물로 진입하는 규칙이 생길 때마다 indegree[y]++; 를 해주어 진입차수 배열을 완성시키고,
최종적으로 W 건물까지 걸리는 최소 시간인 dp[W]를 출력한다.
이후 다음 테스트케이스를 위해 벡터를 모두 초기화해 준다.
void BFS() {
queue<int> q;
for (int i = 1; i <= N; i++)
{
if (indegree[i] == 0) { // 시작 건물들을 큐에
q.push(i);
dp[i] = D[i];
}
}
while (!q.empty()) {
int curr = q.front(); // 지금 짓는건물 curr
q.pop();
for (int i = 0; i < v[curr].size(); i++) {
int next = v[curr][i]; // 다음 갈 건물
if (next > 0) { // next==0 이면 끝 건물이라 계산 ㄴㄴ
dp[next] = max(dp[next], dp[curr] + D[next]); // 점화식
if (--indegree[next] == 0) { // 진입할수 있는 간선이 하나뿐인 건물
q.push(next); // 큐에 삽입
}
}
}
}
}BFS() 에서는 우선 시작 건물, 즉 진입차수가 0인 건물을 큐에 삽입한다.
맨 처음 지어지는 건물이므로, dp[i]는 해당 건물을 짓는 데 걸리는 시간인 D[i]가 저장된다.
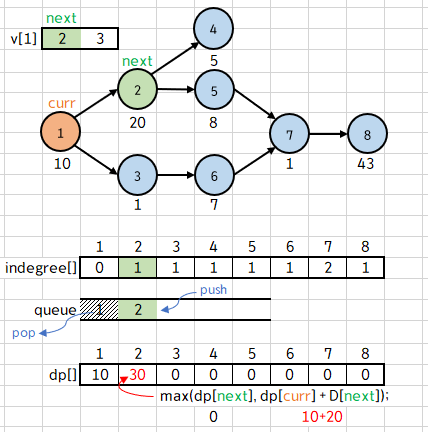
이제 BFS를 진행하게 되는데, 현재는 1번 건물에 있으니 curr에 q.front();인 1을 저장한다.
이후 큐에서 1을 pop 해주고, v[1][0] 에 저장된 2를 next로 한다.
이 때, v[i]가 비어서 next에 0이 저장된다면 i는 끝 건물이므로, if(next > 0) 조건을 넣어 불필요한 계산을 뺀다.
조건문 안에서는 2번 건물을 짓는데 까지 걸린 시간 dp[2] 를 계산하고,
indegree[2] == 1이므로 2를 큐에 push 하면서 다음 루프를 돈다.
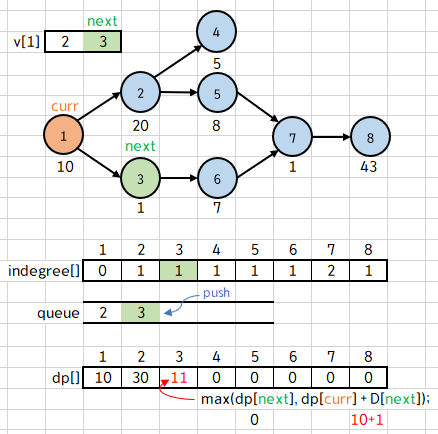
다음 for 루프에서는 v[1][1] 에 저장된 3을 next로 위와 동일한 과정을 수행한다.
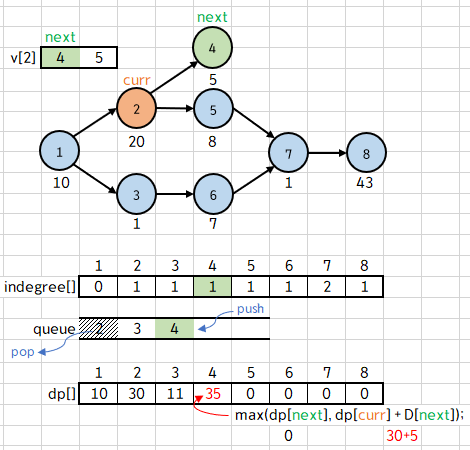
이번 while 루프에서는 q의 top 원소가 2 이므로, curr에 2가 저장되며 2를 pop 한다.
for 루프도 위와 동일하게 수행한다.
최종적으로 dp[7]에는 39가 저장된다.


이런 유용한 정보를 나눠주셔서 감사합니다.