---

Decision Tree는 Tree라는 모형을 이용해서 데이터들을 통해서 결과를 토출해 내는 방법입니다.

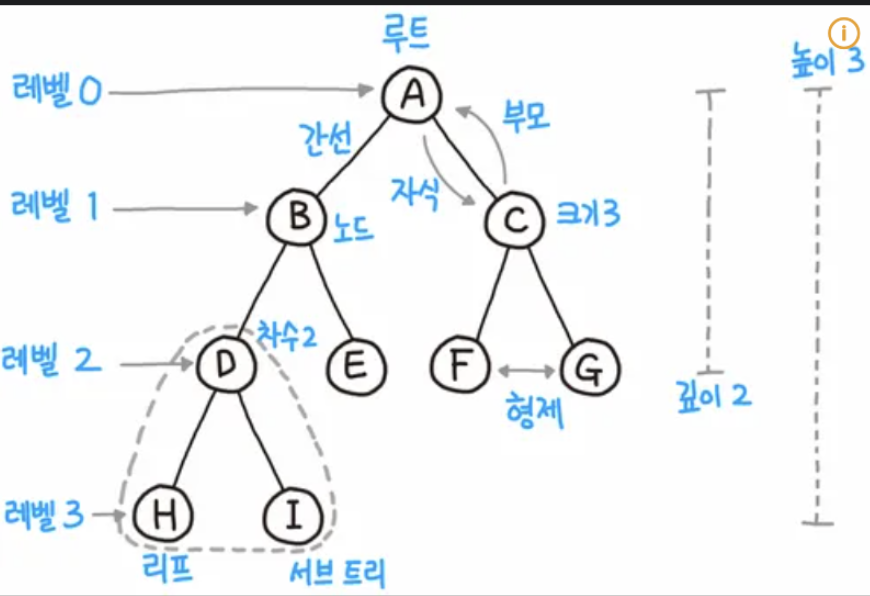
기본적으로 Tree는 아래와 같은 모형을 가지고 있습니다.
출처
기본적으로 맨위에 루트가 있고, 아래로 각각의 Node들이 거점 역할을 하고 쭉쭉나아가는 형태를 의미합니다.

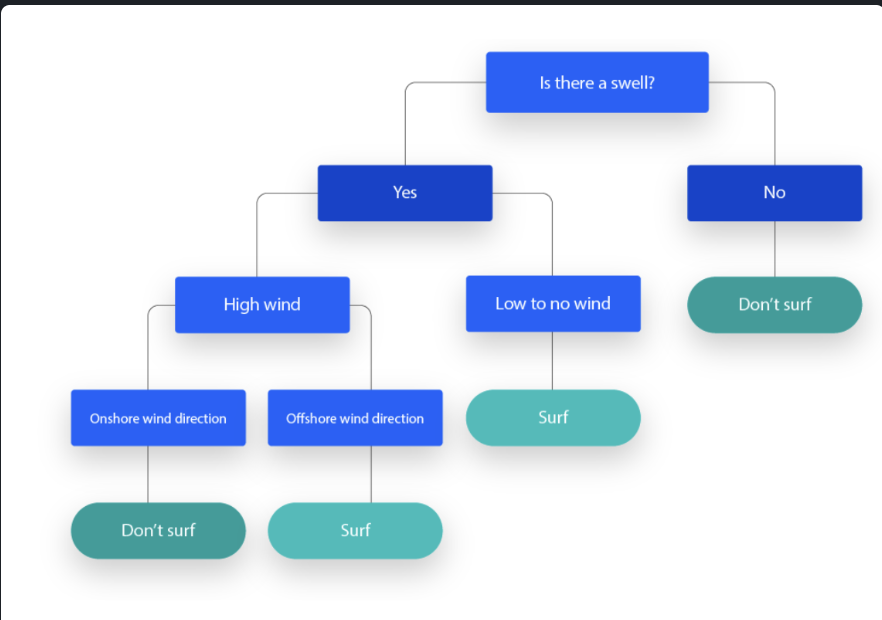
위의 형태를 이용해서 각각의 Node에 특정 조건을 달아서 데이터를 Node에서 지속적으로 2개의 그룹으로 나눠주는걸 Decision Tree라고 부릅니다.

출처

이는 Regression을 푸는 Regression Tree와 classification을 푸는 Classification Tree로 간단하게 구분할수 있습니다.

Regression Tree

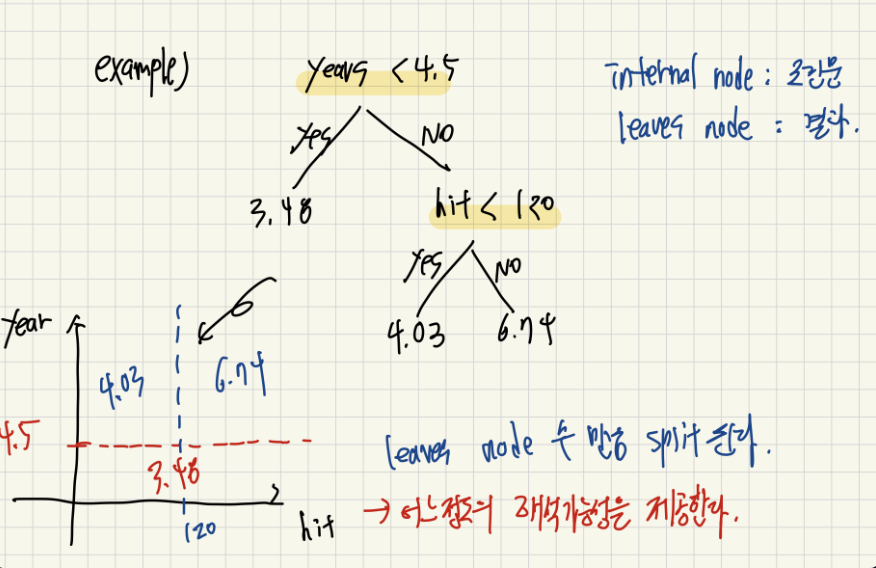
Regression Tree의 경우 다음과 같이 leaves node에서 최종적으로 결정할 실수 값을 얻게 됩니다. 그리고 각각의 Node에서는 부등호를 사용해서 데이터들을 2가지 분류로 나눠주게 됩니다.

그리고 이러한 부등호는 왼쪽 아래 그림에서 볼수 있듯이, 데이터들을 2개의 분류로 지속적으로 나눠주는 역할을 하게 됩니다. 즉, 위에서도 볼수 있듯이 Decision Tree는 어느정도의 해석 가능성을 보여준다는 아주 큰 장점을 가지고 있습니다.

그렇다면 Regression Tree를 어떻게 만들까요?
Regression Tree의 최종 목표는 최대한 동일한 값을 갖는 데이터들 끼리 분리해주는 것입니다. 근데 Regression 특성상 모든 값들이 실수 전체의 값을 갖을 수 있어서 같은 영역에 속한다고 해도 서로 다른 값을 갖아서 최종 목적이 불가능해보일수 있습니다.

하지만 완전히 모든 데이터들을 분리하기 위해서 영역을 데이터 수만큼 사용하는 방법도 쓸수 있습니다. 즉, Regression Tree에서 영역을 나누는 수를 조절하면서 얼마나 Data에 Fit하게 모델을 만들지 결정할수 있습니다.

Regression Tree에서는 영역의 값을 대표하는 대표값을 최종 leaves node에서 결과로 도출합니다. 그래서 결국 영역의 모든 값들과 영역의 대표값의 차이를 손실 함수로 사용할수 있게 됩니다.
그리고 이를 식으로 표현하면 아래와 같은 식을 얻을 수 있습니다.
$$ \hat{y { j }} = a r g m i n \sum { i \in R { j } } ( y { j } - c ) ^ { 2 } $$
y는 각 영역에 속한 데이터들을 의마하고, c는 해당 영역의 대표값을 의미합니다. 그리고 해당 식을 최소화하는 대표값은 바로 데이터들의 평균입니다.

데이터들의 오차제곱을 최소화하는 값은 평균이며, 데이터들의 절대값을 최소화하는 값은 중앙값이다 라는 말을 기억하면 좋을듯 해보입니다.

Top-down greedy algorithm

트리 생성은 먼저 루트 노드에 전체 데이터를 두고 시작합니다. 그다음, 각 피처마다 가능한 모든 분할값을 후보로 삼아(연속형이면 정렬된 값들의 중간값 등) 해당 피처와 임계값 조합으로 데이터를 두 그룹으로 나눴을 때 발생하는 불순도 감소량(예를 들어 정보 이득이나 지니 계수 감소량)을 계산합니다.

이 가운데 불순도 감소량이 가장 큰 피처와 임계값을 선택하여 현재 노드를 왼쪽(≤ 임계값)과 오른쪽(> 임계값) 자식 노드로 분할하고, 분할된 각 자식 노드에 대해서도 동일한 과정을 재귀적으로 반복합니다. 이 과정을 계속하면서 노드의 샘플 수가 너무 적거나(최소 샘플 수 이하), 불순도가 이미 충분히 낮거나(거의 0에 근접), 또는 트리 깊이가 미리 정한 최대치를 넘었을 때 등 미리 정해둔 종료 조건에 해당하는 노드는 더 이상 분할하지 않고 리프 노드로 확정합니다.

이렇게 매 단계에서 “지금 당장” 불순도를 가장 많이 줄여 주는 분할을 선택해 나가는 전략이 바로 Top-down Greedy 방식의 결정 트리 생성 방법입니다.

Tree Pruning

하지만 Tree에 Node가 너무 많게 되면 이 또한 overfitting을 유발하게 됩니다. 그래서 Boundary를 적절한 수준으로 잘라서 generalize를 확보해야하는데, 이러한 과정을 Tree Pruning이라고 합니다. 여러개의 K에 대해서 실험을 진행하고 몇개의 K로 Node를 분리할지 정하고, bottom up 방식으로 leaves 중에서 어느걸 merge해야 정보 손실이 덜할지 계산하여 가장 적은 손실을 가져오는 Node를 합치게 됩니다.

Classification Tree

Classification Tree는 데이터를 여러 클래스(label)로 구분하기 위해 사용하는 결정 트리입니다. 리프 노드(leaf)에서는 최종적으로 하나의 클래스 레이블을 예측하거나, 각 클래스에 속할 확률을 출력합니다.

분할 기준을 선택할 때는 Impurity(불순도)를 최소화하는 방향으로 진행하며, 대표적인 불순도 지표로는 지니 불순도(Gini Impurity), 엔트로피(Entropy), 분류 오차(Classification Error)가 있습니다.

Impurity 개념

어느 노드 R에 속한 샘플 중 클래스 k의 비율을 p_k라 하면, 다음과 같이 정의됩니다.

• 지니 불순도 (Gini Impurity) G(R) \;=\; 1 - \sum_{k=1}^K p_k^2 값이 0에 가까울수록 특정 클래스가 대부분을 차지해 순수한 상태에 가까워집니다.
  
• 엔트로피 (Entropy) H(R) \;=\; -\sum_{k=1}^K p_k \log_2 p_k 정보 이득(Information Gain)을 계산할 때 주로 사용하며, 역시 0에 가까울수록 순수도가 높습니다.

이 외의 방법들은 Regression Tree와 동일합니다.