Machine Learning
1.[ ML ] Linear Regression1

Linear Regression에서 오차 제곱을 사용하는 이유는 IID 가정과 에러가 가우시안을 따른다는 가정하에 MLE를 하게 되어 나온 결과이고, 이렇게 얻은 최적의 베타 값들은 사실 선형대수학에서 말하는 Least Square와 동일한 값을 얻게된다.
2.[ ML ] Linear Regression 2

Linear Regressoin에서의 카테고리컬 데이터 처리와 Feature selection을 통한 안정화된 b 값을 구하는 방법을 소개합니다.
3.[ ML ] Logistic Regression
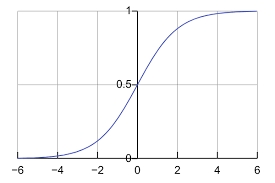
classification 문제를 풀기 위해서 Linear Regression 모델을 그대로 사용하고 출력만 매핑 시키는 Logisic Regression 모델을 소개한다. Logistic Regression의 경우 Log odd가 선형적이라는 가정을 기반으로 한다.
4.[ ML ] Bayes classifier

이전에 배운 DIscriminative 분류기인 Logistic과 다르게 베이즈 정리르 통해서 간접적으로 p(y|x)를 모델링하는 Generative 분류기의 일정인 Bayes classifier의 LDA와 QDA에 대해 알수 잇다.
5.[ ML ] Overfitting & Regularization
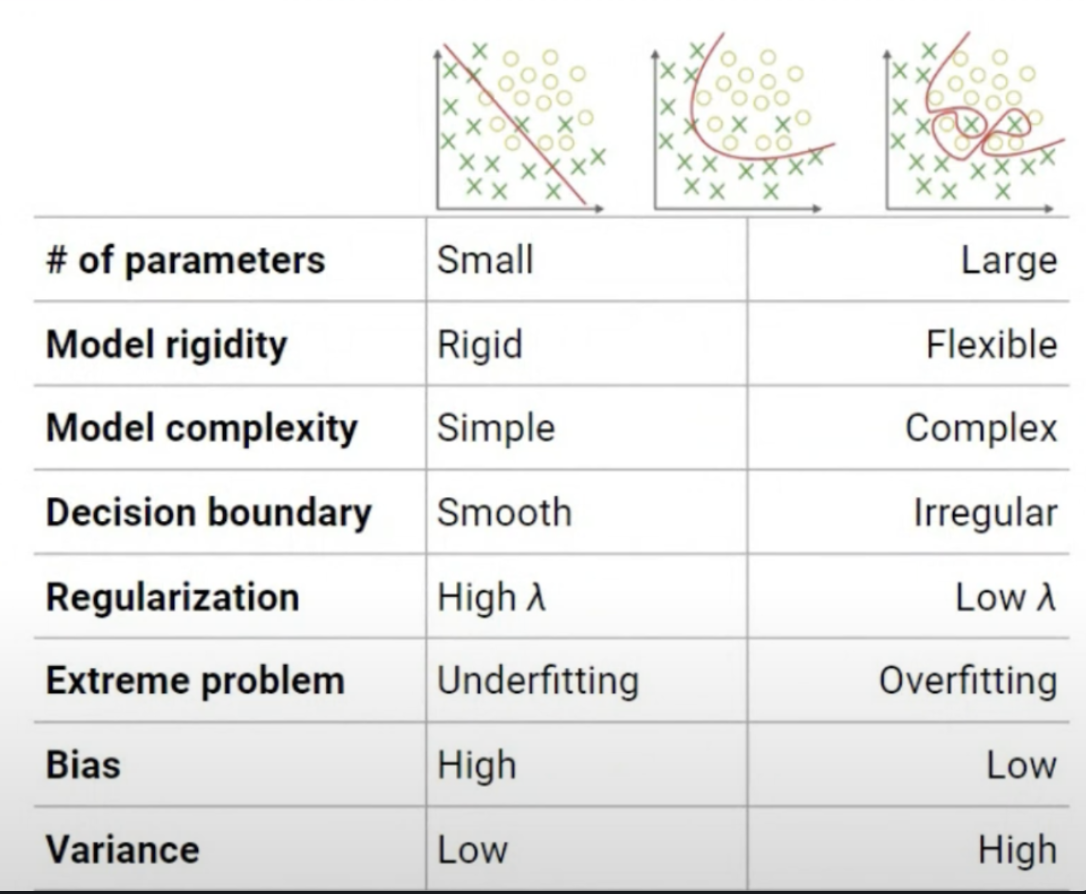
Overfitting이 발생하는 이유로 Train 데이터의 디테일한 패턴을 학습함을 원인으로 들고, 이를 방지하기 위한 Eearly stopping 방법과, 모델의 복잡도를 모델이 스스로 결정하도록 하는 Regularization을 소개한다.
6.[ ML ] Decision Tree
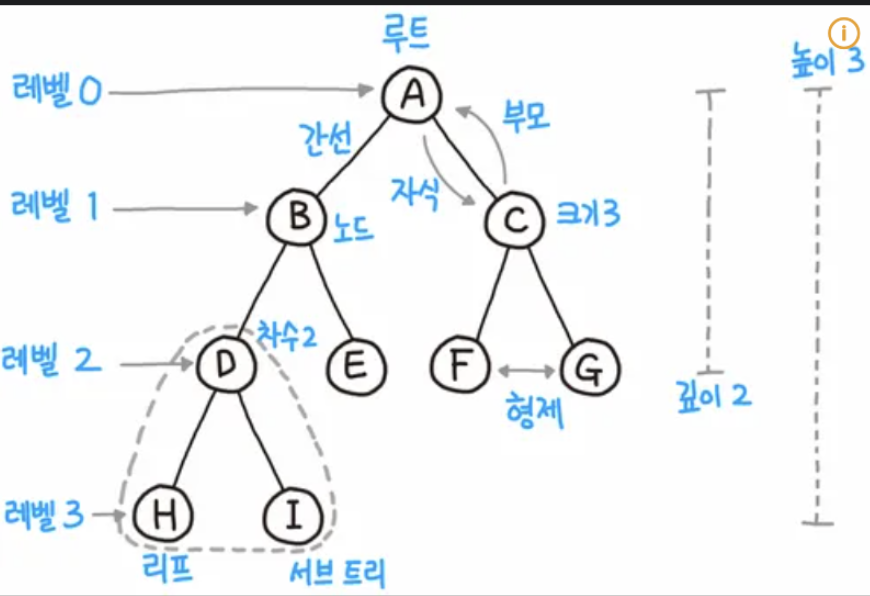
Decision Tree의 개념에 대해 알수 있습니다
7.[ ML ] Ensemble Models & Boosting
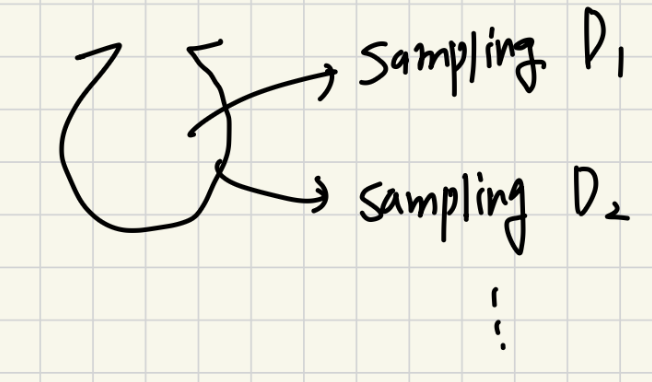
Ensemble의 대표적인 Bagging 방법이 왜 항상 높은 성능을 달성할 수 밖에 없는지에 대해 알 수 있고, Boosting방벙이 무엇인지 알수 있습니다.
8.[ ML ] SVM
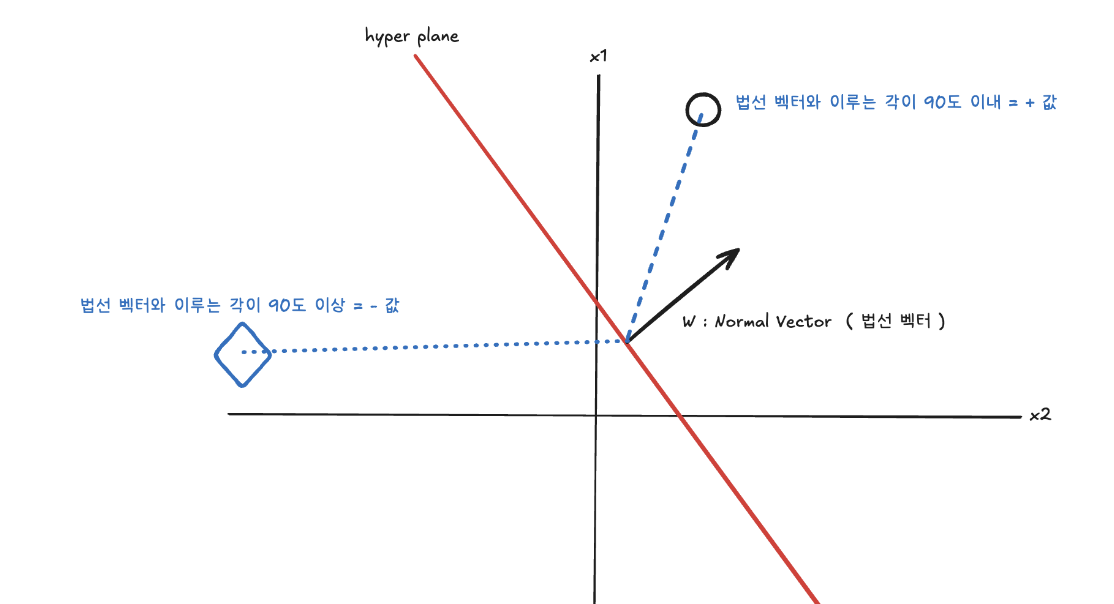
가장 가까운 support vector의 거리를 Maximize하는 방법을 법선 벡터와의 내적으로 부터 의미를 파악할수 있습니다.
9.[ ML ] Unsupervised Learning
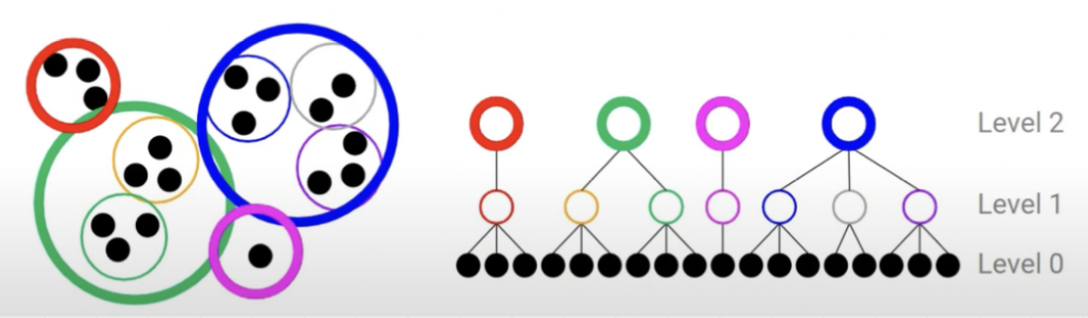
Unsupervised Learning의 경우 데이터에 숨은 패턴을 파악하는 것이며, 대표적으로 군집화와 차원 축소가 있습니다.