---

Bagging

Bagging 방법은 모든 데이터가 IID 하다는 가정을 기반으로 복원추출( 데이터가 한정적인 경우 우리에게 주저인 데이터를 활용하여 최대한 일반화 성능을 올리기 위한 전략 )을 통해서 여러 서브셋을 만들고, 각각의 모델을 학습한 뒤 예측을 평균하여 보다 안정성을 높히게 됩니다.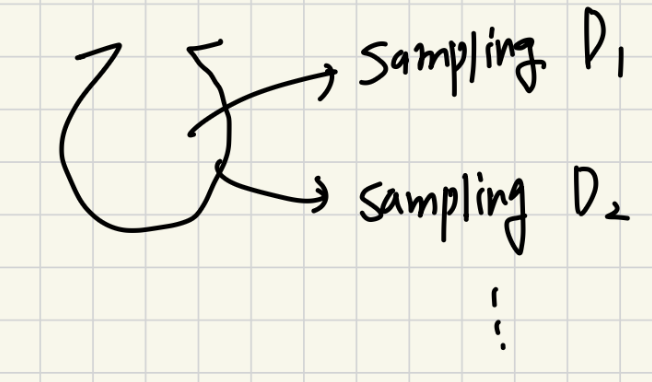
들 때 원래 데이터와 $\frac{2}{3}$ 정도가 중복된 데이터로 나온다고 합니다. 그리고 $\frac{1}{3}$ 정도가 각 서브셋에 취어쳐진 데이터가됩니다. 그래서 각각 취어쳐진 데이터를 통해서 학습하고, 이를 합쳐서 평균을 내면 보다 더 일반화된 모델을 얻을 수 있게 됩니다.

Bagging은 아래와 같은 식을 통해서 정리할 수 있습니다.

Regression인 경우 ( 평균 )

Classification인 경우 ( 다수결 )

식에서 짐작 할 수 있드시, Bagging에서는 결과만 나오면 되기 때문에 서로 다른 다양한 모델을 사용하여 병렬로 처리할 수 있다는 장점을 가지고 있습니다. 하지만 그만 큼 모델을 돌릴 자원을 필요로 합니다.

Bagging이 항상 높은 성능을 달성하는 이유

MSE Loss는 Variance와 Bias를 통해서 정의 됩니다.

Bagging을 사용하는 경우 Bais는 그래도지만 Variance가 낮아진다고 합니다.
그 이유는 Jensen's Equllity로 증명되게 됩니다.

model의 예측 y를 다음과 같이 실제 값 h와 모델의 오차 $\varepsilon_b(x)$ 로 표현하면 아래와 같이 표현할수 있씁니다.

그리고 이 식을 하나의 모델을 사용하는 경우와 여러개의 모델을 사용하는 경우를 식으로 표현하면 아래와 같이 나타낼 수 있습니다,

single 모델을 사용하는 경우

Multi 모델을 사용하는 경우

$E_{\mathrm{total}} = \mathbb{E}\Bigl[\Bigl(\frac{1}{B}\sum_{i=1}^B y_i(x) \;-\; h(x)\Bigr)^2\Bigr]$

이떄 이를 시각화 해보면 아래와 같은 그림을 얻을 수 있습니다.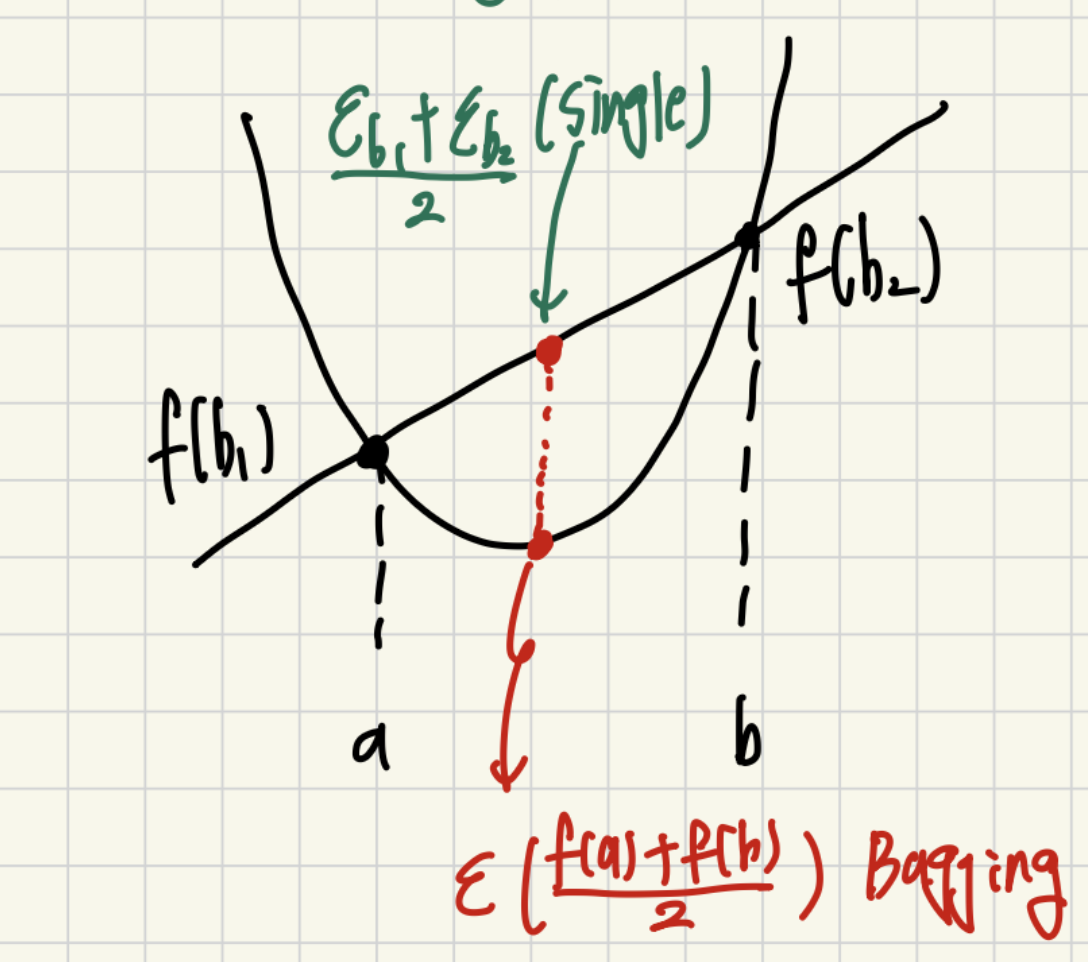

그리고 해당 그림에서 항상 값의 평균을 내고 모델에 넣게 되는 경우 항상 작거나 같은 값을 갖는게 됩니다.

그래서 모델을 1개 쓰는것 보다 여러개를 쓰게 되면 항상 Variance가 같거나, 낮게 됩니다.

Bagged Tree

Bagged Tree는 Bagging 방법을 사용할 떄 각각의 모델들을 Tree로 사용하는 경우를 의미합니다.

Random Forest

Random Forest의 경우 원래는 tree를 생성할때 p개의 특징을 모두 고려해서 최적의 특징을 선택해서 Tree를 만들었습니다. 하지만 Bagging에 이런식의 Tree를 사용하면 거의 모든 Tree의 모양이 동일해지게 됩니다. 그래서 모든 P개의 특징을 고려하지말고, 랜덤으로 $\sqrt{ p }$ 개만 사용해서 Tree를 만들어서 최대한 각 Tree 들이 서로 다른 형태를 갖도록 하여 모델의 다양성을 높힌 방법입니다.

Boosting

Boosting은 weak 모델로 부터 약점을 보완해 가면서 점점 정교한 모델을 만들어가는 방법입니다. 즉, Bagging과 가장 큰 차이는 병렬적으로 처리하지 못하고 순차적으로 처리해야한다는 것 입니다.

AdaBoosting

그중 가장 대표적인 방법은 Adaptive Boosing 방법입니다.



간단한 수도 코든느 다음과 같이 생겼습니다.
(1) 우선 가중치를 초기화 해주게 됩니다.
(2) 처음 모델로 부터 분류하게 됩니다.
(3) 만일 맞게 된다면 D라는 가중치를 줄이고, 틀린 데이터셋에 대해서는 D라는 가중치를 키워주게 됩니다.
(4) 그리고 정규화를 시켜줍니다.
이를 반복하게 됩니다. 이를 통해서 분류에 실패한 데이터에 대해서는 높은 가중치가 생겨서 높은 에러를 갖게 되어 다음 모델에서 더 주의 깊게 보게 됩니다. 이러한 벙법을 통해서 잘 분류하지 못하는 데이터 혹은 클래스를 점진적으로 보강해 나가는 방법이라고 보면 됩니다.