DINO로 불리는 논문에 대해 핵심을 정리해보도록 하겠습니다.
DINO의 경우 특정 TASK를 풀기 위해서 나온 모델이라기 보다는 이미지의 특징을 파악하기 위한 모델이라고 생각됩니다. 즉, 분류, 객체탐지와 같은 문제를 푼다기 보다 라벨이 없는 수많은 이미지를 통해서 해당 이미지를 특정 Feature Vector로 만들어서 기계가 이미지를 이해할 수 있도록 유도하는 방법을 의미합니다.

이를 구축하기 위해서 해당 논문에서는 Student, Teacher 방법을 활용해서 Knowledge Distillation 기법을 적용합니다.

아주 간단하게 흐름에 대해서 정리하면 아래와 같습니다.
(1) 수많은 라벨이 없는 이미지를 CROP해서 2가지 Type의 이미지를 구축합니다. Global Crop, Local Crop.

(2) 동일한 ViT 모델을 Teacher, Student 모델에 배치합니다.

(3) Teacher Model에는 Global Crop 이미지만 입력으로, STudent Model에는 Global, Local Crop 모두를 입력으로 사용합니다.
( 이떄 Teacher과 Student의 입력이 다르지만 동일 이미지에서 나온 것이기 떄문에 동일한 결과가 나오지 않고 Loss를 발생 시킬 수 있게 됩니다. )

(4) Student 모델 ( ViT ) 를 통과하여 feature map을 얻고 해당 featue map을 엄청 나게 큰 차원으로 확장시킵니다. Teacher Model 또한 동일하게 동작합니다.

(5) 얻어진 엄청나게 큰 Feature vector를 softmax하게 되면 확률분포와 근사한 결과를 얻을 수 있게 되고, Teacher과 Student 모델 출력 확률분포를 CrossEntropy를 통해서 Loss를 얻습니다. 이때 Teacher의 출력은 Sharpening과 Centering이라는 추가적인 가공을 거쳐 더 안정적이고 명확한 '정답' 역할을 하게 됩니다

(6) 이렇게 얻어진 Loss로 Student를 바로 업데이트 하고 Teacher는 이전의 파라미터에 EMA를 적용해서 적은 부분만 업데이트 하게 됩니다.

흐름 파악

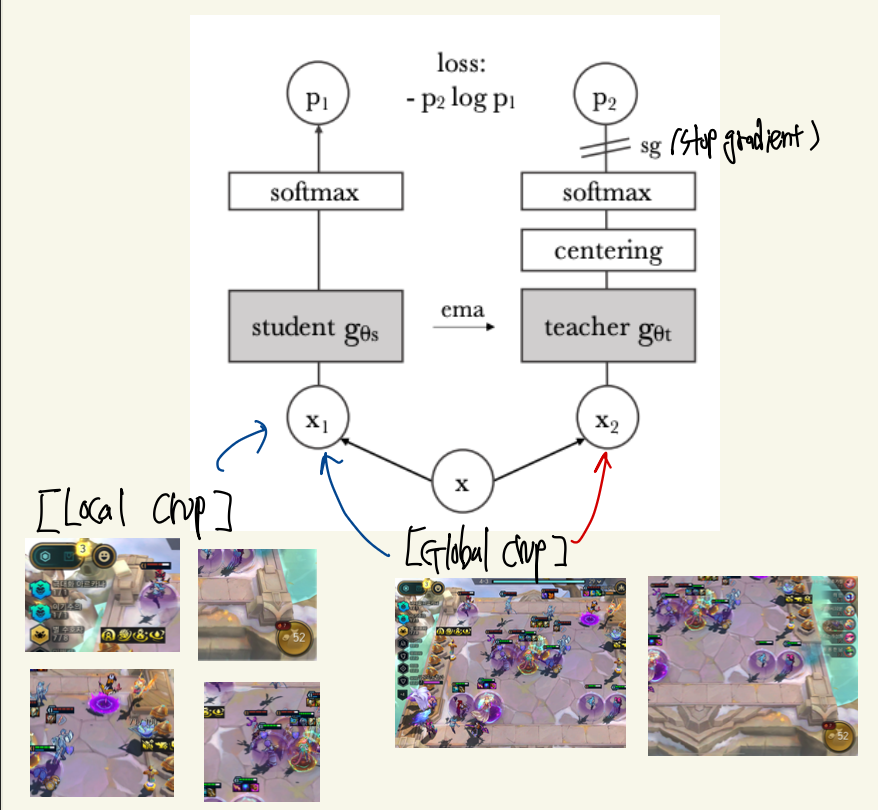
위의 사진처럼 하나의 이미지에 대해서 50%보다 작은 세부적인 CROP을 진행한 Local Crop과 50% 크기보다 큰 Global Crop으로 데이터를 증강하게 됩니다. 이후 Local Crop과 Global Crop은 Student의 입력으로 들어가고 Global Crop은 Teacher 모델로 들어가게 됩니다.

이후 각각의 데이터들은 모델을 통과하게 됩니다. 즉 특정 차원을 갖는 하나의 Feature Vector를 얻게 됩니다.

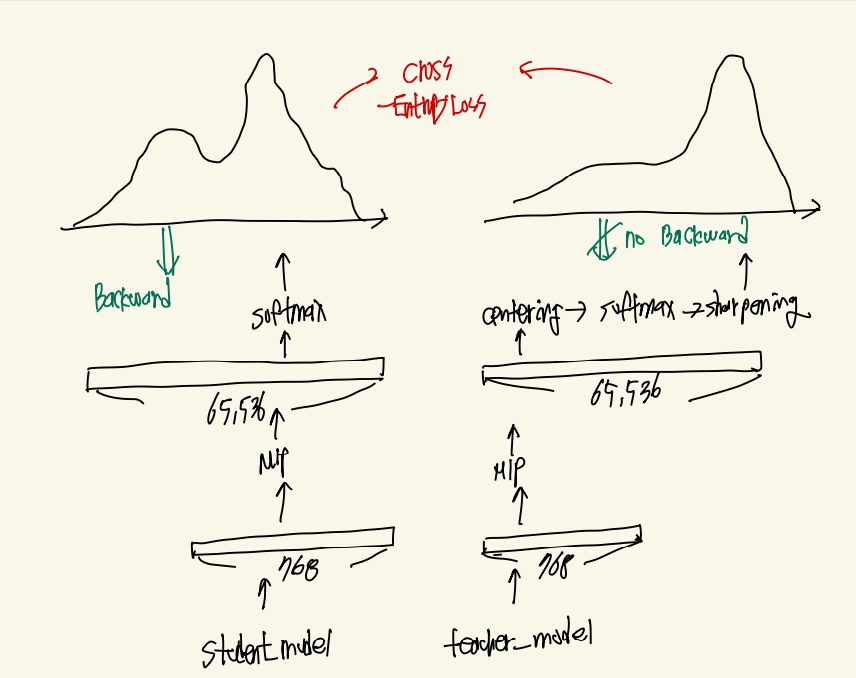
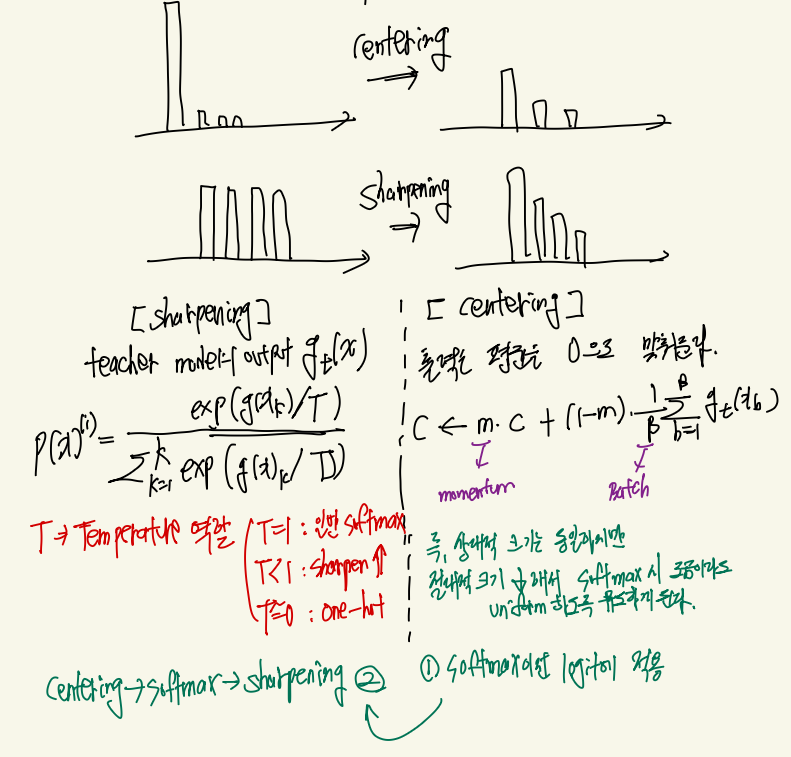
그렇게 얻어진 Feature Vector는 MLP 헤드를 통과하면서 65,536이라는 엄청나게 큰 Feature vector로 확장되게 됩니다. 이렇게 확장하는 이유는 이미지의 특징을 우선 엄청 큰 vector로 표현하게 유도하면 자연스럽게 비슷한 이미지의 feature가 큰 값을 갖도록 유도하면서 다양한 feature를 표현할 수 있기 때문입니다. 그래서 다음과 같이 65,535크기의 feature vector를 softmax를 진행하면 그림과 같이 확률분포와 같은 결과를 얻을 수 있게 됩니다. 이때 Teacher 모델의 경우 모델의 안정성을 위해서 MLP 이후 모든 값들에 대해서 출력 평균을 0으로 맞춰주는 Centering을 진행 한 후 softamx를 진행하는 경우 특정 temperature로 나누어 주어 특정 feature가 도드라지도록 유도하는 sharpening을 적용하여 정답 feature가 커질 수 있도록 유도합니다.

이렇게 얻어진 2개의 확률분포는 Corss-Entropy를 통해서 Loss가 구해지고 Student Model은 Backward()를 통해서 파라미터를 업데이트 하게 됩니다. 하지만 Teacher 모델의 경우 Loss가 직접적으로 흘러들어가지 않도록 StopGradient를 적용합니다 그 이유는 Teacher 모델의 경우 loss를 기반으로 업데이트 하는게 아니라 이전의 Teacher Model 파라미터값에 방금 변경된 Student 파라미터를 특정 가중치 만큼 더해주면서 업데이트를 하게 됩니다. 이렇게 업데이트를 하게 되면 천천히 학습이 진행됨과 동시에 Student 모델이 스스로 학습하는 효과를 볼 수 있다고 합니다.

Teacher Model의 update는

θ_t ← λ * θ_t + (1 - λ) * θ_s

다음과 같이 이뤄지게 됩니다. 여기서 θ_t의 경우 이전의 teacher model의 파라미터를 의미하며 θ_s는 업데이트 된 student 모델의 파라미터를 의미합니다. 그래서 Teacher 모델의 파라미터를 최대한 유지하면서 학습이 될수록 업데이트 되는 Student 모델의 파라미터를 조금씩 더해서 학습되게 됩니다.

디테일 요소

Student 모델의 경우 2개의 Global 이미지와 여러개의 Local 이미지가 들어가고 Teacher 모델의 경우 오직 2개의 Global 이미지만 들어가게 됩니다.
이떄 Loss를 구하는 방식은 아래와 같이 동작한다고 합니다.
1. Global 끼리는 1 대 1 매칭으로 확률분포 값을 비교하여 Loss를 구합니다.
2. Local 이미지에 대한 출력 확률 분포는 Teacher 모델의 2개의 출력과 모두 비교하여 평균 Loss를 얻는다고 합니다.

그래서 최종적으로 2개의 Loss과 N개의 Loss를 얻고 이들을 모두 더해서 하나의 Loss로 만들고 이를 기반으로 backward를 진행한다고 합니다.

추가적으로 Teacher Model을 업데이트 하는 경우 λ값을 0.99처럼 매우 큰 값을 사용하는데 학습 초기에는 해당 값을 더 작게 설정하여 빠르게 학습하고 뒤로 갈 수록 λ을 키워서 보다 안정적으로 학습하도록 유도한다고 합니다.

정리

DINO의 경우 라벨이 없는 대규모 이미지를 매우 큰 feature vector로 매핑 시키고 동일한 이미지는 동일한 feature를 갖도록 유도하면서 기계가 이미지를 feature로 이해할 수 있도록 유도하여 향 후 다양한 모델의 backbone으로 사용되게 됩니다.