SwinTransformer의 전체적인 논문을 리뷰하기 보다 SwinTransformer의 동작 원리에 대해서 구체적으로 살펴보도록 정리하였습니다.

[ 간단 요약 ]

SwinTransformer의 경우 기존 ViT에서 이미지 단위를 특정 Patch 단위로 나누어서 이를 Attention을 하게 되는데 이렇게 전체 이미지에 대해서 Patch 단위로 분할 하고 Attention을 하게 되면 이미지 해상도가 증가함에 따라서 기하급수적으로 Attention 비용이 늘어남을 지적하고 있습니다. 이를 해결하기 위해서 Window-Attention을 제안하여 같은 Window 내에서만 attention을 진행하여 이미지 해상도와 비례해서 연산량이 증가하도록 하였습니다. 이렇게 Window내에서만 Attention을 진행하다 보면 바로 옆에 있는 다른 Window와는 교류를 할 수 없다는 단점이 존재하기에 Shifted-Window attention을 적용하여 Window의 위치를 이동하여 다시 window-attention을 진행하는 방법을 제안하였습니다. 추가적으로 각각의 SwinTrnasformer 연산을 진행한 후 Feature Map의 인접한 2 * 2 Patch를 병합하여 하나의 Patch로 만들고 채널을 2배로 늘리면서 더 많은 수용영역을 보면서 다양한 특징을 학습 할 수 있도록 하였습니다.

[ 헷갈리는 용어 정리 ]

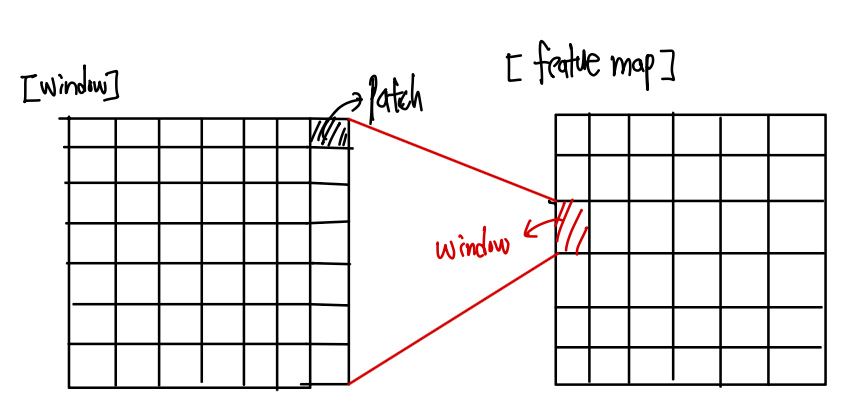
• Patch : 하나의 최소 단위가 됩니다.
• Window : 여러개의 Patch가 모여 Attention이 진행되는 단위
  논문에서는 주로 하나의 Window가 7 * 7 개의 Patch로 구성되도록 설정하였습니다.

전체적인 정리 순서

설명 흐름 자체는 다음과 같이 전체적인 아키텍처 흐름에 맞게 정리하였습니다.

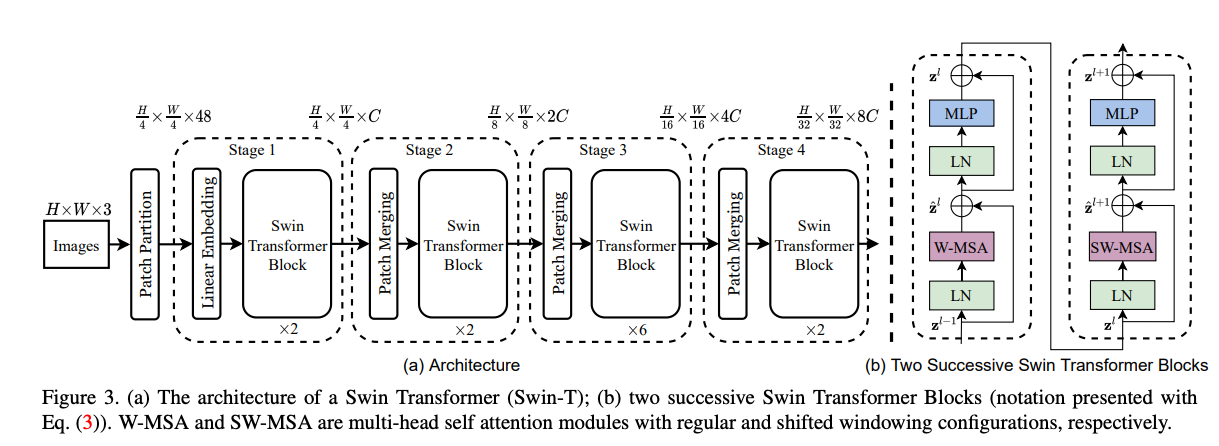
입력 이미지

SwinTransformer의 경우 이미지를 모델의 입력에 넣기 전에 우선적으로 Patch단위로 이미지를 나누게 됩니다. 초기 입력에 대해서는 2 2 pixel을 하나의 Patch로 설정하게 됩니다. 이때 2 2를 C차원으로 embedding 시키고 Concat시키게 됩니다. 그렇게 되면 총 4개의 C차원이 합쳐지면서 4C 채널의 Vector가 생성되고 이를 nn.Linear를 통해서 다시 2C로 변환해주는 과정을 거치게 됩니다.

즉, 인접한 4개의 C 차원의 pixel이 1개의 2C 차원의 Patch로 변환되게 됩니다. 이러한 과정에서 해상도는 1/2개 되고 채널은 2배가 되게 됩니다.

self.proj = nn.Conv2d(in_chans, embed_dim, kernel_size=patch_size, stride=patch_size)

x = self.proj(x).flatten(2).transpose(1,2)
if self.norm is not None : 
    x = self.norm(x)
return x 

코드로 나타내보면 인접한 2 * 2를 하나의 패치로 만들기 위해서 Non-Overlap이 되도록 convolutional 연산을 수행해주게 됩니다. 이후 얻어진 값들은 projection Layer를 거친후 반환되게 됩니다.

Relative Positional Embedding & Attention Mask

Relative Positional Embedding

해당 부분이 가장 이해하기 어려웠던 부분이였다. 기존의 ViT의 경우 단순히 절대적인 위치를 알려주는 positional encoding을 단순히 더해주면서 모델이 알아서 위치를 학습하도록 유도하였습니다. 하지만 Swin Transformer에서는 절대적인 위치보다는 Window 내에서 attention을 하다보니 각 패치들의 상대적인 위치를 고려하는게 보다 중요합니다.

그래서 본 논문에서는 상대적인 좌표값 차이를 이용해서 위치를 나타냅니다.
본 논문에서 Window의 사이즈를 (7,7)을 사용하기에 하나의 Window 내에서 x,y 좌표는 각가 [-6, 6] 사이의 값을 갖게 됩니다. 즉 각각 13가지의 경우의 수가 존재합니다. 이를 양수로 표현하게 되면 [0,12] 까지로 표현이 가능하며 Y값의 경우 13를 곱해주고 X의 값과 더해주게되면 ex) [0,0] -> (13X0) + 0 = 0, [1,2] -> (13X1) + 2 = 15. 즉, 0 ~ 12까지는 y = 0, 13 ~ 25까지는 y =1 이런식으로 결국 모든 좌표 값을 양수로 표현할 수 있게 됩니다.

그리고 결국 하나의 윈도우 ( 7 * 7 ) 개, 49개의 패치에 위치 정보를 제공하기 위해서 x좌표 49개, y좌표 49개를 표현하고 위와 같은 방식으로 Y값이 윈도우 크기의 2배 만큼을 곱해서 하나의 숫자로 표현하게 됩니다.

그리고 아래 코드를 활용해서 각각의 영역에 대해 양수 Index를 위에서 언급했던 방식으로 지정해주게 됩니다.

coords_h = torch.arange(self.window_size[0])
        coords_w = torch.arange(self.window_size[1])
        # [0], [1]로 각 차원에 접근하기 위해서 stack() 활용
        coords = torch.stack(torch.meshgrid([coords_h, coords_w]))
        # coords_flatten 예시 값.
        # tensor([[0, 0, 0, 1, 1, 1, 2, 2, 2],
        #          [0, 1, 2, 0, 1, 2, 0, 1, 2]])
        coords_flatten = torch.flatten(coords, 1)
        # relative_coords ( window_size=7인 경우 ) [2,49,49]  
        relative_coords = coords_flatten[:, :, None] - coords_flatten[:, None, :]
        # [2,49,49] -> [49, 49, 2]로 변경 
        relative_coords = relative_coords.permute(1, 2, 0).contiguous()
        # [-6 ~ 6] 까지의 값들에 + 6을 진행하여 [0, 12] 까지의 양수로 치환한다.
        relative_coords[:,:,0] += self.window_size[0] - 1
        relative_coords[:,:,1] += self.window_size[1] - 1
        # y = 0 이면 (0~13), Y=1이면 ( 14 ~ 27 ) 이런식으로 서로 겹치지 않는 양수로 만들고 1D로 표현하기 위한 작업을 진행 
        relative_coords[:,:,0] *= 2 * self.window_size[1] - 1
        # sum(-1)을 진행하여 최종적으로 [49, 49] 크기를 갖는다. ( 각 패치들의 위치 정보가 x,y를 동시에 하나의 값으로 저장 )
        relative_position_index = relative_coords.sum(-1)
        self.register_buffer("relative_position_index", relative_position_index)

위와 같은 코드를 통해서 Window 내에서 상대적인 위치를 양수 Index로 표현할 수 있게 되었습니다. 이렇게 좌표 값 자체를 Index로 접근이 가능하게 되면 169 차원의 nn.Paramter()에서 Index로 접근하여 값을 가져와 Bias로 사용할 수 있게 됩니다.
즉, Relative Position을 구축하기 위해서는 (1) Index Table ( 학습 X ) (2) relative position table ( 학습 O ) 2개가 필요합니다.

Attention Mask

Shifted window를 적용하는 경우 효율성을 위해서 순환구조를 활용해서 서로 다른 window내의 patch들이 상호작용 하도록 유도합니다. 이때 단순히 padding을 둬서 window 사이즈를 유지하면서 하게 되면 window의 수가 늘어나게 됩니다. 그래서 반대편에 있는 실제 값을 가져와 Masking 처리한 후 Attention을 진행하게 되면 추가적인 연산이 필요하지 않고 동시에 연관이 없는 정보가 서로 섞이지 않는다는 장점이 존재합니다.

 H, W = self.input_resolution
            img_mask = torch.zeros((1, H, W, 1)) 
            h_slices = (slice(0, -self.window_size),
                        slice(-self.window_size, -self.shift_size),
                        slice(-self.shift_size, None))
            w_slices = (slice(0, -self.window_size),
                        slice(-self.window_size, -self.shift_size),
                        slice(-self.shift_size, None))
            cnt = 0
            for h in h_slices:
                for w in w_slices:
                    img_mask[:, h, w, :] = cnt
                    cnt += 1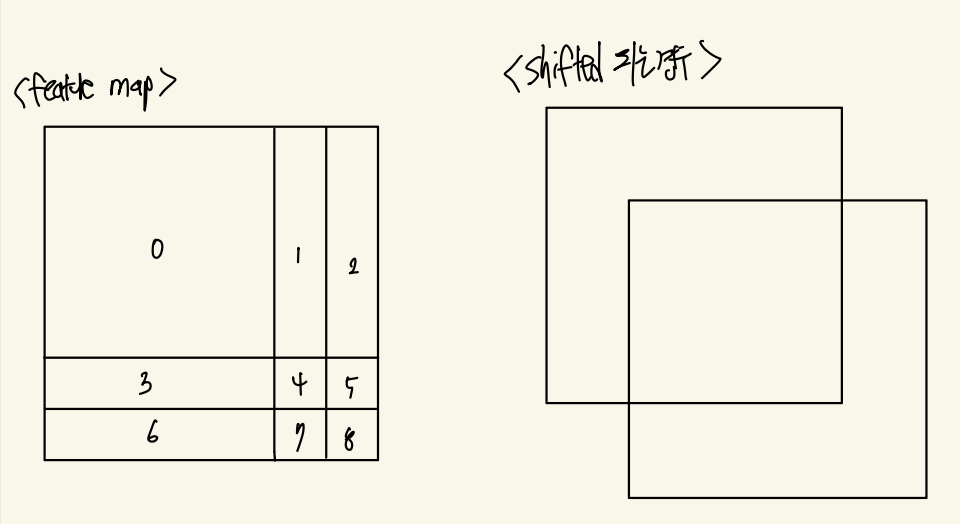

위의 코드는 위 그림에서 왼쪽 처럼 Feature Map을 분할 한 후 각각의 픽셀에 0 ~ 8 까지의 숫자를 부여하여 영역을 표현해주게 됩니다. 영역을 나누는 경우 균일하게 나눈지 않는 이유는 Shifted_window를 적용하는 경우 window_size // 2 만큼 윈도우를 이동하게 되는데 그렇게 되면 오른쪽 그림 처럼 이동하게 됩니다. 이때 빈 윈도우를 매꾸기 위해서 넘쳐버린 부분이 이동하고 Mask를 처리해서 Window Attention을 진행하게 됩니다.

if self.shift_size > 0 : 
	if not self.fused_window_process:
    	shifted_x = torch.roll(x, shifts=(-self.shift_size, -self.shift_size), dims=(1,2))
                '''torch.roll()
                x = torch.tensor([[0, 1, 2],
                                  [3, 4, 5],
                                  [6, 7, 8]])

                y = torch.roll(x, shifts=(-1, -1), dims=(0, 1))
                        tensor([[4, 5, 3],
                                [7, 8, 6],
                                [1, 2, 0]])
                '''
       	x_windows = window_partition(shifted_x, self.window_size)

그래서 Masking을 보다 용이하게 하기 위해서 일부러 영역을 왼쪽 처럼 설정하게 됩니다. 여기서 Shifted를 진행 한 후의 영역 값과 Shifted 진행 하기 전 영역 값을 뺴서 0이 되면 이동 후에도 인접한 곳이라고 판단되어 Masking이 진행되지 않고, 만일 0이 아닌 값을 갖는 경우 매우 작은 (-100) 으로 설정하여 Attention에 영향을 주지 않도록 만들어주게 됩니다.

mask_windows = window_partition(img_mask, self.window_size)
            # [ _, window_size * window_size]
mask_window = mask_windows.view(-1, self.window_size * self.window_size)
            # [_, 1, window_size, window_size ]- [_, window_size, 1, window_size]
            """attn_mask 예시
            img_mask = [
                    [0, 0, 1, 1],
                    [0, 0, 1, 1],
                    [2, 2, 3, 3],
                    [2, 2, 3, 3]
                ]

                unsqueeze(1) -> 
                [[0],
                [1],
                [2],
                [3]]

                unsqueeze(2) ->
                [[0,1,2,3]]

            broad_casting을 통해서 - 을 하게 되면 결국 서로 다른 window에서 온 값은 0이 아닌 값이 나오게 됩니다.
            이에 0이 아닌 값은 아주 작은 음수로 만들어서 softmax 통과시 거의 0값이 되도록 만들어줍니다.
            """
attn_mask = mask_window.unsqueeze(1) - mask_window.unsqueeze(2)
attn_mask = attn_mask.masked_fill(attn_mask != 0, float(-100.0)).masked_fill(attn_mask == 0, float(0.0))

위와 같은 방식으로 Attention Mask를 적용할 수 있게 됩니다.

SwinTransformerBlock

SwinTransformerBlock에 들어가기 앞서 Feature map을 window 단위의 attention을 진행하기 위해서 분할해줘야 합니다.

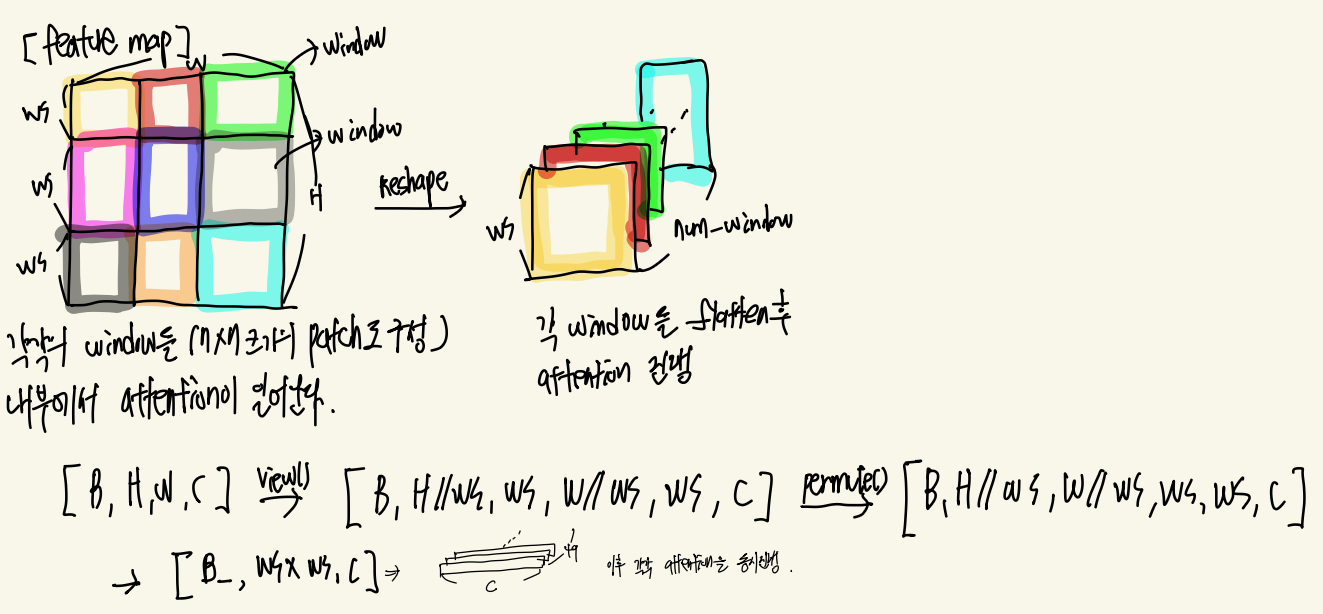
그래서 위의 사진처럼 Feature map을 window size 크기 만큼으로 분할 해줍니다. 그리고 편리하게 계산을 하기 위해서 하나의 window 만을 남기고 나머지는 하나의 차원을 추가하여 쌍하주게 됩니다.

    B, H, W, C = x.shape
    x = x.view(B, H // window_size, window_size, W // window_size, window_size, C)
    windows = x.permute(0, 1, 3, 2, 4, 5).contiguous().view(-1, window_size, window_size, C)
    return windows

결국 최종적으로 [B_ , WS X WS , C] 차원으로 변경되는데 이는 결국 하나의 윈도우에 집중할 수 있게 됩니다. 그 이유는 하나의 윈도우인 WS X WS X C를 분할 했고 나머지 B_개에 대해서 독립적 & 동시에 계산이 가능하기 떄문입니다.

x_windows = x_windows.view(-1, self.window_size * self.window_size, C)

그래서 위의 2개의 코드를 지나게 되면 최종적으로 [B_ , WS X WS , C] 크기로 window_attention에 들어가게 됩니다. Window_Attention에서는 Maksing 유무에 따라서 Masking을 진행하고 같은 Feature Vector들 끼리 self-attention을 진행하게 됩니다. 이는 기존의 ViT와 비슷한 방법으로 수행됩니다. 추가적으로 num_head를 활용하는 경우 C차원을 num_head로 나눠서 각각의 Q,K,V를 생성한 후 독립적인 attention을 진행한 후 다시 concat되는 식으로 동작하게 됩니다.

정리

그래서 위에서 정의했던 모든 모듈들을 활용하게 되면 SwinTransformer를 구축할 수 있게 됩니다.

이미지가 -> Patch Partition -> Linaer Embedding -> SwinTransformerBlock -> [Patch Merging -> SwinTransformerBlock]X2
-> [Patch Merging -> SwinTransformerBlock]X2 -> [Patch Merging -> SwinTransformerBlock]X6 -> [Patch Merging -> SwinTransformerBlock]X2 다음과 같이 진행하게 됩니다.

이렇듯 window 내에서만 attention을 진행하여 연산 효율성을 높힘과 동시에 shifted_window를 사용하여 서로 다른 window 끼리도 상호작용 할 수 있도록 유도하여 이미지의 전반적인 특징을 추출 할 수 있게 됩니다.

디테일한 내용

1. nn.Dropout() VS nn.Dropout2d

nn.Dropout()의 경우 tensor의 모든 element에 대해서 독립적으로 생각하여 각 element를 확률적으로 0으로 만들어줍니다. 하지만 nn.Dropout2d의 경우 채널 단위를 확률적으로 모두 0으로 만들어주는 함수입니다.

즉, nn.Dropout()의 경우 확률 적용 대상이 각가의 element이고 Dropout2d의 경우 확률 적용 대상이 각 채널에 속한 모든 elements입니다.

그렇다면 CNN에서는 왜 Dropout2d를 활용할까?

이미지의 경우 바로 근접한 pixel이 사라지더라도 거의 비슷한 값을 가지고 있어 dropout의 효과를 제대로 적용하지 못하고 단순히 learning_rate를 줄여주는 효과를 보여준다고 합니다. 이에 특정 특징 자체를 제거하기 위해서 ( 예를들어, 귀를 나타내는 특징, 꼬리를 나타내는 특징 ) 특정 채널의 모든 값을 0으로 만들어주게 된다고 합니다.

그래서 CNN에서는 주로 nn.Dropout2d()를 사용한다고 합니다.

2.BatchNorm VS LayerNorm

Batch NormBatch Norm의 경우 미니 배치에서 들어온 데이터에서 동일한 채널끼리 평균과 분산을 구하게 됩니다. 그리고 이렇게 구해진 같은 채널의 평균과 분산을 활용해서 정규화를 진행하게 됩니다. 즉 평균=0 분산=1이 되도록 유도합니다.

그렇다면 왜 정규화를 진행할까요? Layer를 거칠 수록 Layer는 이전 Layer의 결과를 입력으로 받습니다. 그리고 최종 Loss를 기반으로 update를 합니다. 즉 이전 Layer의 출력을 기반으로 Loss를 최소화 하기 위해서 업데이트를 진행합니다. 하지만 optim.step() 시에는 모든 Layer의 파라미터가 변경되게 됩니다. 즉 Layer가 이전 Layer에서의 결과를 입력으로 해서 Loss를 최소화 되도록 하였는데, 이전 Layer의 결과가 바뀔 수 있다는 것 입니다. 그래서 이러한 이전 layer의 변동을 최소하하기 위해서 BatchNorm()으로 정규화를 진행한다고 합니다.

이렇게 BathNorm()을 활용하면 이전 Layer의 출력 결과가 보다 안정적으로 변경되게 됩니다.

BathNorm

→ 미니 배치 내에서 모든 데이터들의 동일한 Channel들에 대해서 정규화 진행 ( 여러 이미지중에서 channel 별 정규화, 눈 특징은 눈특징 끼리, 귀 특징은 귀 특징 끼리 … )

LayerNorm

→ 하나의 데이터에 대해서 모든 Channel에 대해서 정규화 진행 ( 즉, 하나의 이미지에 대해서 정규화 )

Transformer기반의 모델들의 경우 데이터의 입력이 가변적이기 떄문에 BatchNorm을 하게 되면 < PAD > 토큰들과의 평균도 구해지기 떄문에 학습이 불안정하게 될 수 있다는 이유로 주로 LayerNorm을 사용합니다. 하지만 ViT 기반의 이미지 모델들의 경우 이미지의 해상도를 동일하게 맞추지만 그럼에도 불구하고 LayerNorm을 쓰는 이유는, ViT 기반의 모델들은 메모리를 많이 차지하기 떄문입니다. 그래서 Batch 사이즈를 크게 키울 수 없기에 BatchNrom을 사용하게 되면 LayerNorm보다 안정적이지 못해서 주로 LayerNorm을 사용한다고 합니다. 만일 GPU의 성능이 올라오고 Batch를 충분히 키울 수 있다면 이미지에서 BatchNorm을 사용해서 특징별 정규화를 해주는 것이 더 도움이 되지 않을까? 생각합니다.