[ 논문 리뷰 ] Diffusion Model

JSM0315·2025년 5월 16일

논문리뷰

목록 보기

19/24

OverView

열역학적 관점에서 입자 분포를 퍼져서 자연스럽게 Uniform 형태가 됩니다.
그런데 우리가 Uniform한 상태에서 역과정을 모델링할 수 있다면 데이터가 어디서부터 만들어졌는지 알 수 있습니다.
이걸 모델링한 모델이 바로 Diffusion Model 입니다.

즉, 잉크가 물에 퍼진 Uniform 한 상태에서 역으로 모델링해서 잉크가 어디로 부터 떨어졌는지를 모델링하고자 하는 아이디어이다. 혹은 빅뱅을 찾아가는 과정이라고 생각해도 꽤나 설득력 있습니다. ( 빅뱅에서 우주가 퍼져나가니깐 )

그리고 한가지 가정을 하는데, 바로 매우 짧은 Seqeunce 내에서는 동일한 분포로 forward & backward를 모델링할수 있다는 가정입니다.

Diffusion Model의 경우 크게 Forward path와 Reverse path로 구분이 가능합니다.
Forward path의 경우 지속적으로 Gaussian Noise를 첨가하여 점점 완전 $N(0,I)$ 를 따르는 이미지가 나오도록 합니다.

x_t \;=\; \sqrt{1-\beta_t}\,x_{t-1} +\sqrt{\beta_t}\,\epsilon_t, \qquad \epsilon_t \sim \mathcal N(0,I)

그리고 Reverse path의 경우에는 가우시안 분포르 따른다는 모양만 알고, 평균은 알지 못합니다. 그래서 모델을 통해서 노이즈를 예측하여 평균을 구하고 다시 노이즈를 추가하는 방법으로 노이즈를 제거해주게 됩니다.

결국 이미지를 완전 노이즈로 만들고, 완전 노이즈에서 다시 원본으로 복원하는 과정에서 모델은 매 스텝 가우시안 노이즈의 평균을 예측하도록 유도하게 됩니다.

Forward Path

사진과 같이 원본 이미지에서 지속적으로 노이즈를 추가해주게 됩니다.
노이즈의 경우 가우시안 분포 $N(0, I)$ 를 따릅니다. 그리고 지속적으로 노이즈를 더해서 최종적으로 완전 $N(0, I)$ 을 따르게 하기 위해서 원래 픽셀값을 줄이면서 노이즈를 추가해 주게 됩니다. 노이즈를 줄이는 정도는 처음에는 작은 값을 사용하고 점점 키워주게 됩니다. 그리고 그 값은 미리 정해져있으며 주로 $\beta_{t}$ 로 표현합니다.

그래서 원본 이미지에서 노이즈를 더해주는 과정을 수식으로 표현해보면 아래와 같이 표현이 가능합니다.

x_t \;=\; \sqrt{1-\beta_t}\,x_{t-1} +\sqrt{\beta_t}\,\epsilon_t, \qquad \epsilon_t \sim \mathcal N(0,I)

$\sqrt{1-\beta_t}\,x_{t-1}$ 를 보면 1에서 어느 작은 값을 뺴주기 때문에 이전 이미지에 대한 값들에 예를들어 0.9 정도를 곱해서 약하게 만들어줍니다. 그리고 뒤에서는 가우시안에서 랜덤을 뽑은 값을 더해주게 됩니다. 즉, 원래 픽셀값의 의미를 줄이면서 점점 노이즈를 추가해준다고 해석이 가능합니다. 그래서 이미지에서는 이러한 과정을 총 10000번 진행하게 되면 완전 노이즈로 이미지가 변경되는 것을 확인할수 있습니다.

그리고 Forward path의 경우 모르는 미지수가 하나도 없고, 우리가 가우시안 분포를 따른다고 가정하고 평균 또한 0 으로 설정해주었기 떄문에 특정 t시간에서의 이미지를 한번에 구할수 있습니다 ( 어차피 $\beta_{t}$ 를 지속적으로 곱하는거니깐 이를 한번에) . 그래서 특정 t 시간에서의 이미지는 아래와 같이 공식화 할수 있습니다.

x_t \;=\; \sqrt{\bar\alpha_t}\,x_0 +\sqrt{1-\bar\alpha_t}\,\epsilon, \qquad \bar\alpha_t=\!\!\prod_{s=1}^{t}(1-\beta_s)

최종적으로 위의 식을 통해서 완전 노이즈인 $X_{T}$ 를 구할구 있게 됩니다.

Reverse Path

reverse path의 경우 완전 노이즈 에서 원본으로 복원하는 과정입니다. Diffusion Model의 가정에 의해서 결국 reverse 에서 노이즈를 제거하는 과정 또한 특정 Gaussian 분포를 따를것입니다. 보통 분산은 Forward 에서 사용한 $\beta_{{t}}$ 와 동일하게 사용합니다. 하지만 평균을 알수가 없습니다. 왜냐하면 Forward에서도 픽셀의 값을 구하는 경우 이전 픽셀을 줄이고, 가우시안 분포에서 랜덤으로 샘플링한 값을 더했기 때문입니다.

그런데 여기서 한가지 의문이 들 수 있습니다.왜?? Forward 에서 분포와 Backward에서의 분포가 가우시안이라고 가정은 했는데, 왜 굳이 평균을 알아야 하는가??. Reverse Path에서의 가우시안 분포의 평균을 아는게 Noise를 제거해서 원본을 얻는거랑 무슨 상관이 있는거지?? 라는 생각을 할수 있습니다.

그 의문을 해결하기 위해서 아주 기나긴 수학 공식을 풀어보겠습니다. 한가지 딱 중요하게 기억하고 갈 것은 결국 우리의 목표는 $E_{q}[\log p_{\theta}(x_{0})]$ 을 최대화 하는 것입니다. 즉 forward path에서 x들이 q라는 가우시안 분포로 샘플링 되었을때, p라는 평균을 모르는 가우시안 분포에서 원본 이미지가 나올 가능성을 최대화하자!! 입니다. 직관적으로도 이해가 잘 될것이라고 생각합니다.

이제 이를 풀기 위한 수식을 보여드리겠습니다. 최대한 수식을 써놔서 천천히 읽으시면 이해할수 있다고 생각이 됩니다.

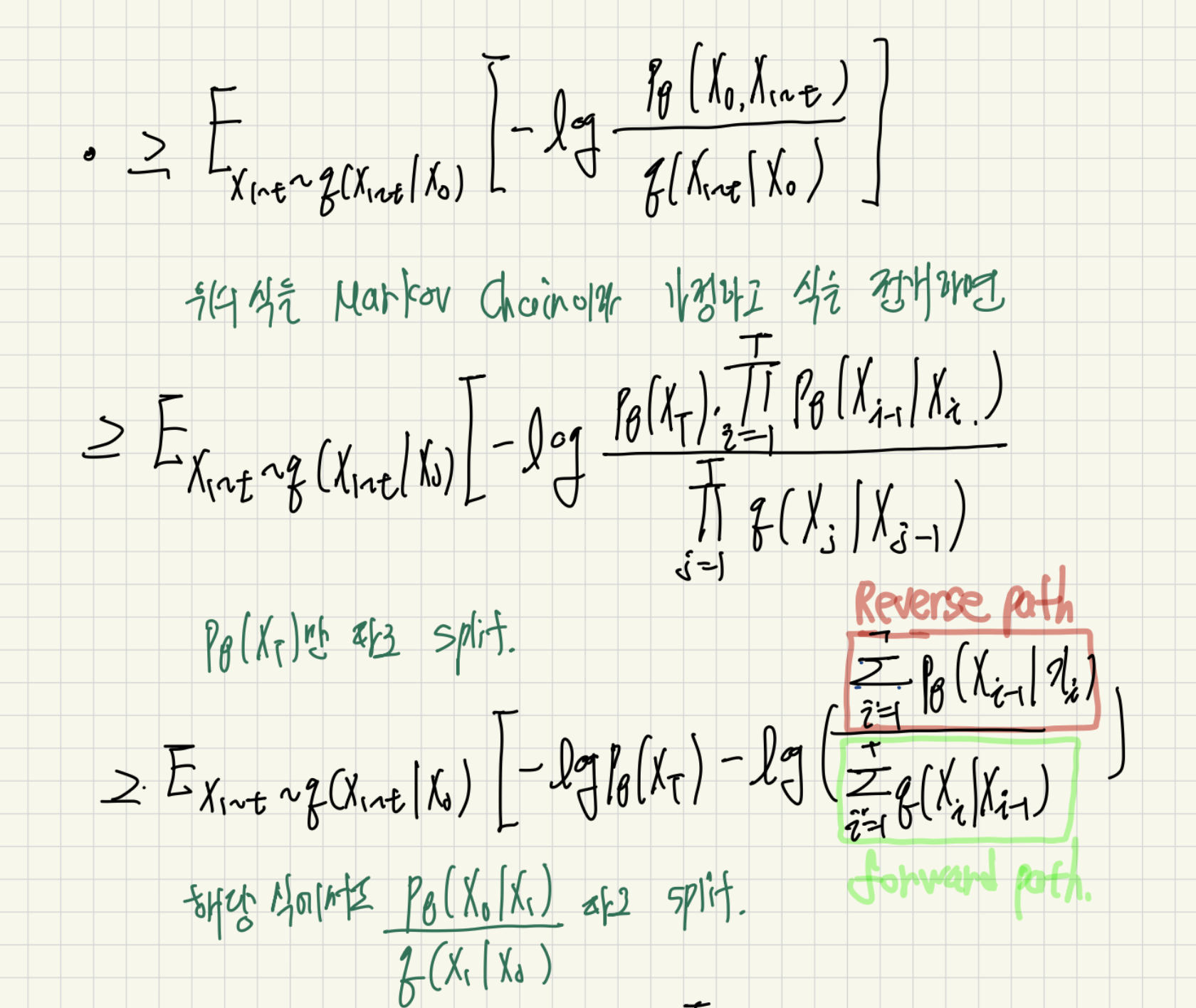
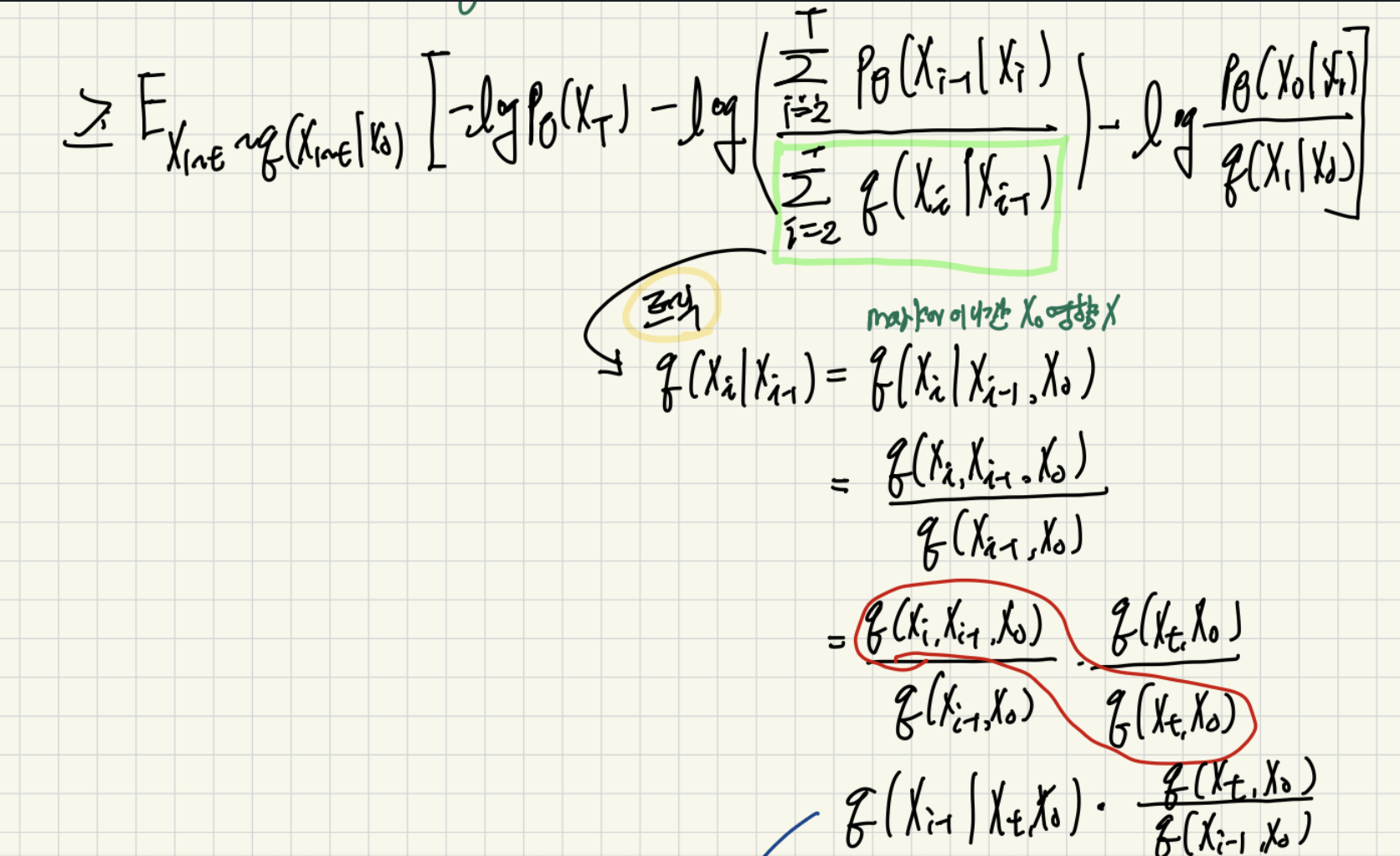
그리고 참고로 마지막에 KL Divergence를 구하는 과정에서 음수가 사라진 이유는 p와 q의 위치를 바꿔서 KL을 구하기 때문이다.

그리고 최종식을 수식화 하면 아래와 같이 나타낼 수 있습니다.

\log p_\theta(x_0) \;\ge\; \mathbb E_q\!\Bigl[ -\,\bigl( L_T +\sum_{t=2}^{T}L_{t-1} +L_0 \bigr) \Bigr]

\begin{aligned} L_T &=D_{\mathrm{KL}}\bigl(q(x_T\!\mid x_0)\;\|\;p(x_T)\bigr)\\ L_{t-1} &=D_{\mathrm{KL}}\bigl(q(x_{t-1}\!\mid x_t,x_0)\;\|\;p_\theta(x_{t-1}\!\mid x_t)\bigr)\\ L_0 &=-\mathbb E_q\bigl[\log p_\theta(x_0\!\mid x_1)\bigr] \end{aligned}

그래서 위의 식을 통해서 얻은게 무엇인가?? 우리가 p라는 reverse 분포에서 원본 이미지가 나올 가능성을 가장 높히기 위해서는 같은 시간 t에 대해서 forward의 분포와 reverse의 분포를 최대한 비슷하게 만들어야 한다!! 는 결과를 얻게 되었습니다. 아래 사진 처럼 T와 T + 1 사이의 Gassuian이 비슷해야된다! 를 의미합니다.

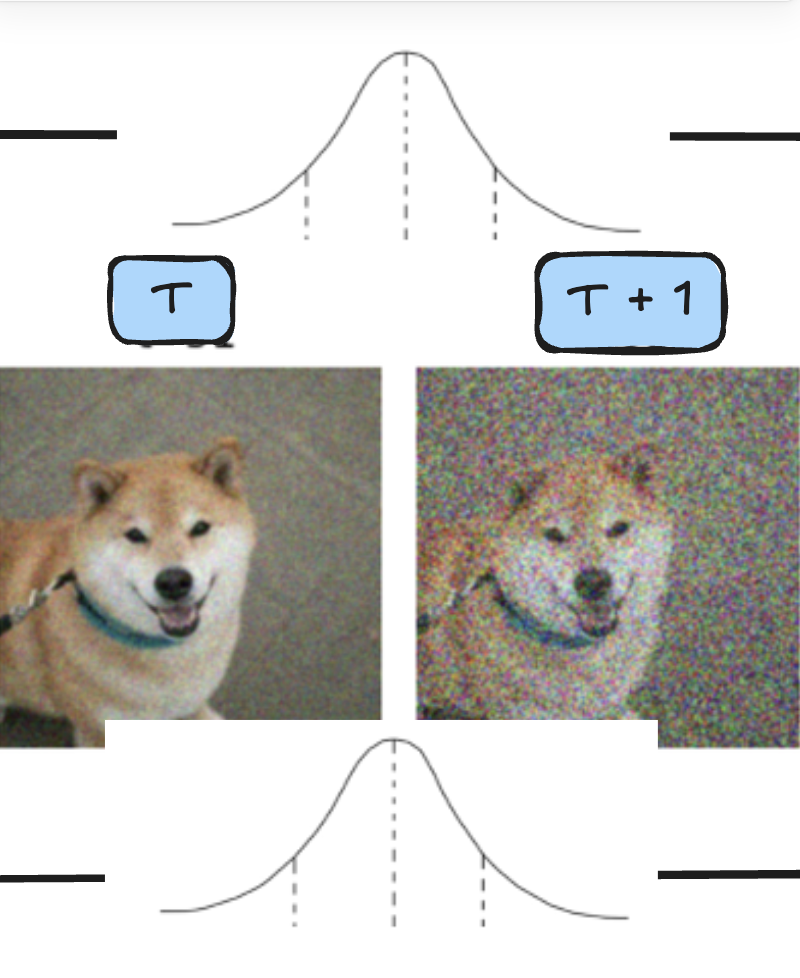
그래서 이제는 두 분포를 동일하게 하기 위해서 위에서 모른다고 했던 평균을 모델링 해야합니다.

그러기 위해서는 p함수는 모르기에 q함수를 사용해서 모데링을 하게 됩니다. 그 이유는 어차피 동일한 분포를 따르기 떄문입니다.

q(x_{t-1}\!\mid x_t,x_0) = \mathcal N\!\bigl( \tilde\mu_t(x_t,x_0), \tilde\sigma_t^{\,2}I \bigr)

그래서 q함수를 사용해서 평균을 모델링을 하게 되면 ( Multivariate Gaussian 식 사용) 아래와 같은 식을 얻을 수 있다고 합니다. ( Multivariate Gaussian은 아직 잘 몰라서... 그래서 우선 그냥 공식을 적용한다고 생각하면 됩니다 )

\tilde\mu_t(x_t,x_0)= \frac{1}{\sqrt{1-\beta_t}} \!\Bigl( x_t-\frac{\beta_t}{\sqrt{1-\bar\alpha_t}}\, \epsilon \Bigr), \qquad \tilde\sigma_t^{\,2} =\frac{1-\bar\alpha_{t-1}}{1-\bar\alpha_t}\,\beta_t

하지만 여기서 우리는 $\epsilon$ 을 알수가 없습니다. 왜냐하면 해당 값은 Forward에서 N(0,1) 분포에서 샘플링된 노이즈 값이기 떄문입니다. 그래서 위는 이를 미지수로 두기 위해서 아래와 같이 표현하게 됩니다.

p_\theta(x_{t-1}\!\mid x_t) =\mathcal N\!\bigl( \mu_\theta(x_t,t), \sigma_t^{2}I \bigr)

그러면 이제 우리는 q를 통해서 p 함수의 평균을 모델링 하였습니다. 그러면 이제 우리가 모르는 것은 바로 Forward에서 나온 노이즈 값 자체입니다. 그것만 알게 된다면 우리는 p함수를 구할수 있게 됩니다. 그리고 U-Net 모델을 통해서 바로 저 노이즈를 예측하도록 만들게 됩니다!! ( 와!! 소리가 나와야됩니다 ㅋ)

\mu_\theta(x_t,t)= \frac{1}{\sqrt{1-\beta_t}} \!\Bigl( x_t-\frac{\beta_t}{\sqrt{1-\bar\alpha_t}}\, \underbrace{\epsilon_\theta(x_t,t)}_{\text{U-Net output}} \Bigr)

위의 식으로 표현이 가능하게 됩니다, 즉 U-Net이 t시간에 대한 이미지를 입력으로 받게 되면 평균을 예측하게 되고, Forward 과정에서 나온 노이즈 값은 샘플링 되어서 모델이 알수 있기에 MSE Loss를 통해서 학습이 가능하게 됩니다. 그래서 결국 우리가 U-Net을 통해서 노이즈를 학습하게 된다면 결국 두 분포의 KL Divergence를 최소화 하는 방향이 된다는 것 입니다!!

이를 간단하게 수식으로 표현해보면 위에서 구한 p와 q의 KL Divergence는 결국 U-Net에서 구한 노이즈의 MSE 손실에 비례함을 할수 있습니다. 그래서 간단하게 아래와 같은 식으로 Loss를 단순화 할 수 있게 됩니다.