📢 개요
Data Reduction이란 다루고자 하는 데이터 셋에 대해 마이닝 결과는 유지하면서 크기를 줄이는 방법이다. 실제 데이터 셋에는 불필요한 정보들도 많이 포함되어 있을 뿐더러, 이미 가지고 있는 값을 중복해서 가지고 있는 경우도 비일비재하다. 또한, 유사한 의미를 가지고 있어 합칠 수 있지만 원본 데이터에는 여러 개의 attribute로 나뉘어져 있는 경우도 존재한다. 물론 데이터가 많으면 많을수록 데이터 분석의 질은 향상되겠지만, 그만큼 많은 시간이 소요된다. 따라서 데이터 분석의 질은 유지하되, 어느 정도 가볍게 만들어 주는 과정이 필요하다. Data Reduction 과정은 크게 Feature Extraction과 Feature Selection 두 가지 방법으로 나뉘는데 이번 포스트에서는 'Feature Extraction' 방법에 대해 정리해보고자 한다.
❓ 참고
차원이 커질 수록 발생하는 문제는?
차원 축소를 하는 이유는?
차원의 저주(The Curse of Dimensionality)
✏️ 특성 추출(Feature Extraction)이란?
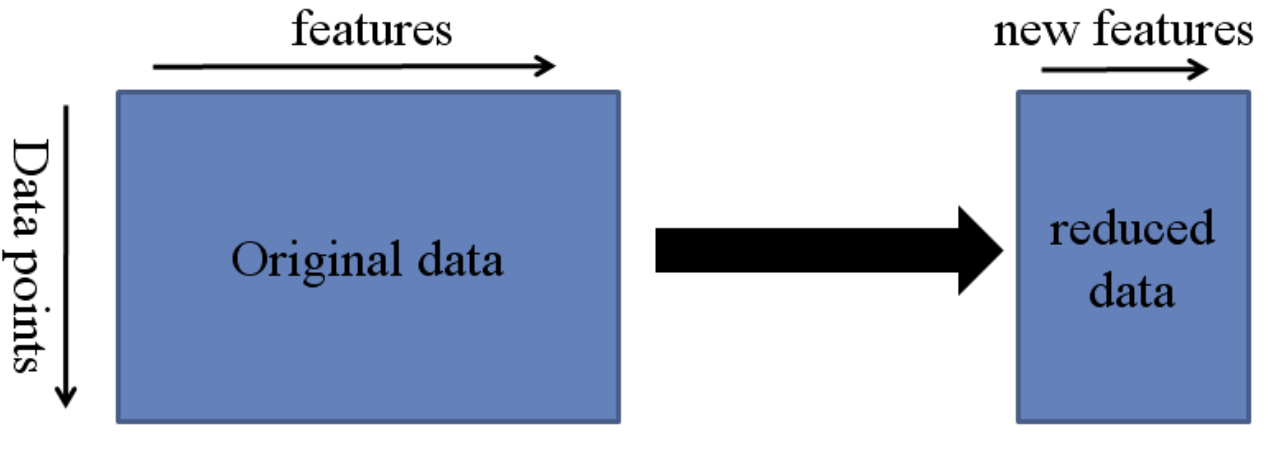
👉 기존 특성(feature)들의 조합으로 유용한 feature들을 새롭게 생성하는 과정
👉 특성(feature)들 사이에 내재한 특성이나 관계를 분석하여 이들을 잘 표현할 수 있는 새로운 선형 혹은 비선형 결합 변수를 만들어 데이터를 줄이는 방법
👉 고차원의 원본 feature 공간을 저차원의 새로운 feature 공간으로 투영
⭐ 장점
- 특성(feature) 간 상관관계를 고려하기 용이
- 특성(feature)의 개수를 많이 줄일 수 있음
🔥 단점
- 추출된 변수의 해석이 어려움
📂 종류
📚 주성분 분석(Principal Component Analysis, PCA)
📙 주성분 분석(PCA)이란?
👉 가장 대표적인 차원(변수, feature) 축소 기법 중 하나
👉 고차원의 원본 데이터를 저차원의 부분 공간으로 투영하여 데이터를 축소시키는 기법
👉 기존 데이터의 분산(variance)을 최대한 보존하는 새로운 축을 찾아, 고차원 공간의 표본들을 선형 연관성이 없는 저차원 공간으로 변환하는 기법
📗 주성분(Principal Component, PC)이란?
👉 기존의 변수를 조합하여 만들어진, 서로 연관성이 없는 새로운 변수
👉 전체 데이터(독립변수들)의 분산을 가장 잘 설명하는 성분
👉 데이터를 투영하였을 때 가장 높은 분산을 가지는 데이터의 축에 해당
❗ 투영했을 때 분산이 크다는 것은 원래 데이터의 분포를 잘 설명할 수 있다는 것을 뜻하고 정보의 손실을 최소화 할 수 있다는 것을 의미
📌 왜 PCA를 사용하는가?
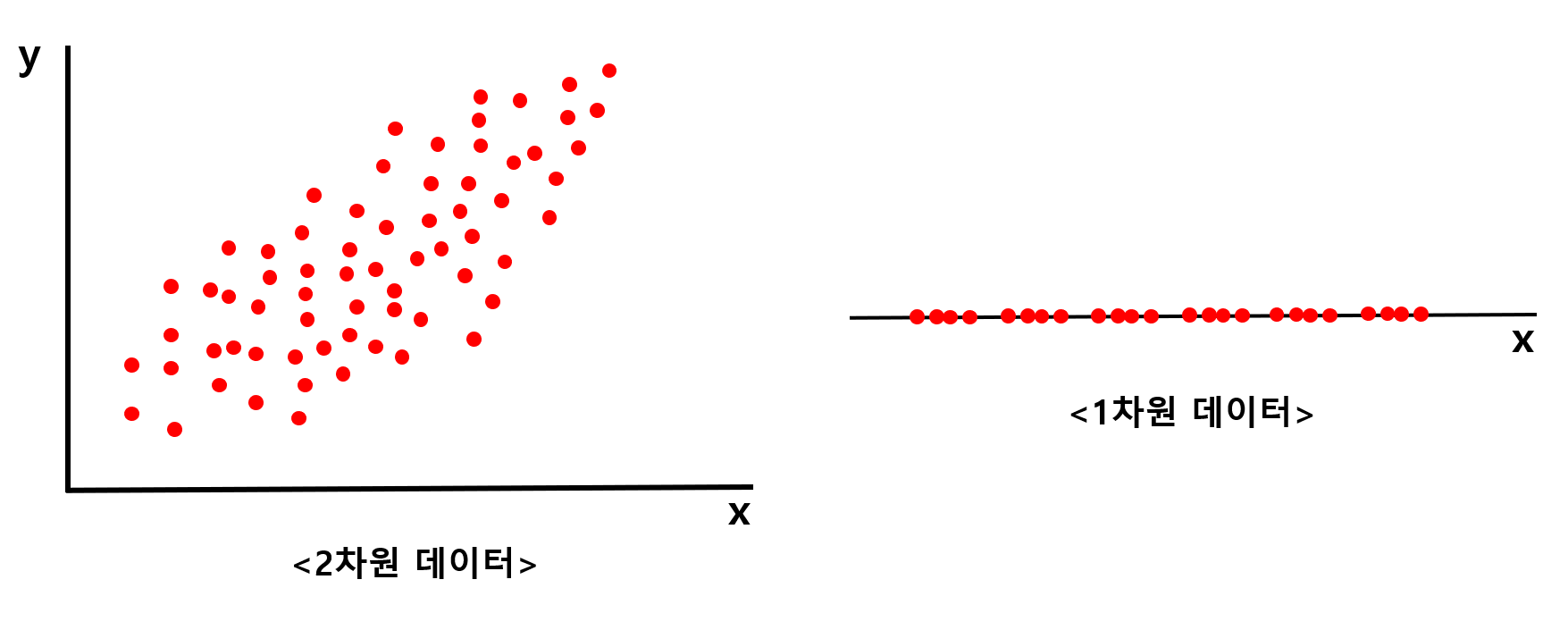
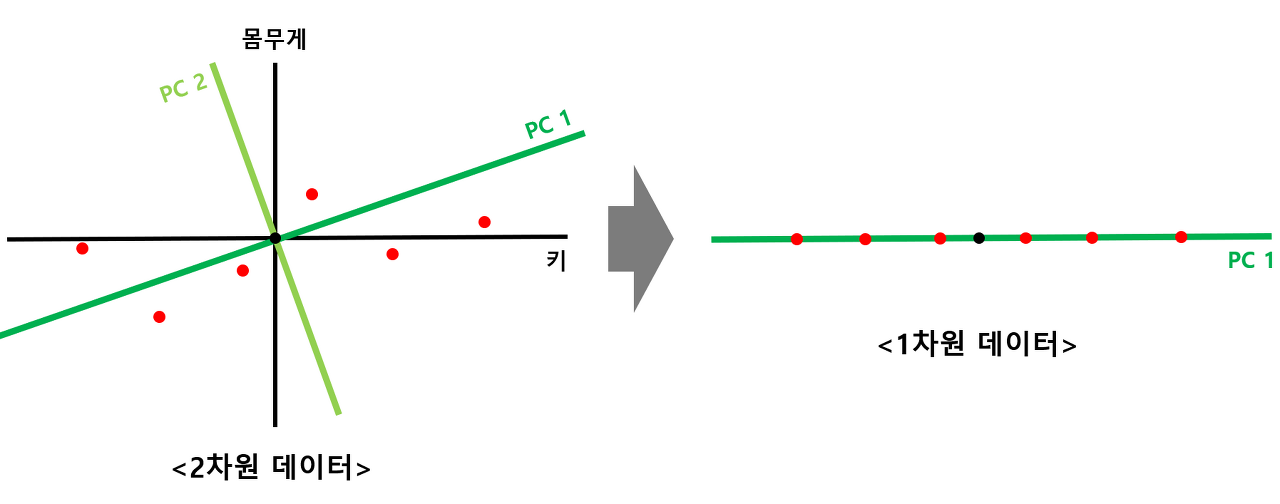
🧩 위 그림의 왼쪽 2차원 데이터를 오른쪽 1차원 데이터로 축소한다고 생각해보자
- 독립변수의 축으로 축소 결과, 기존 2차원일 때는 거리를 두고 위치하던 데이터들이 차원이 축소되면서 겹치게 되는 문제가 발생
- 이는 기존의 데이터가 가지고 있던 정보의 손실이 발생한 것으로 볼 수 있음
- 즉, 2차원 데이터의 특징을 모두 살리면서 1차원으로 변환이 어려움
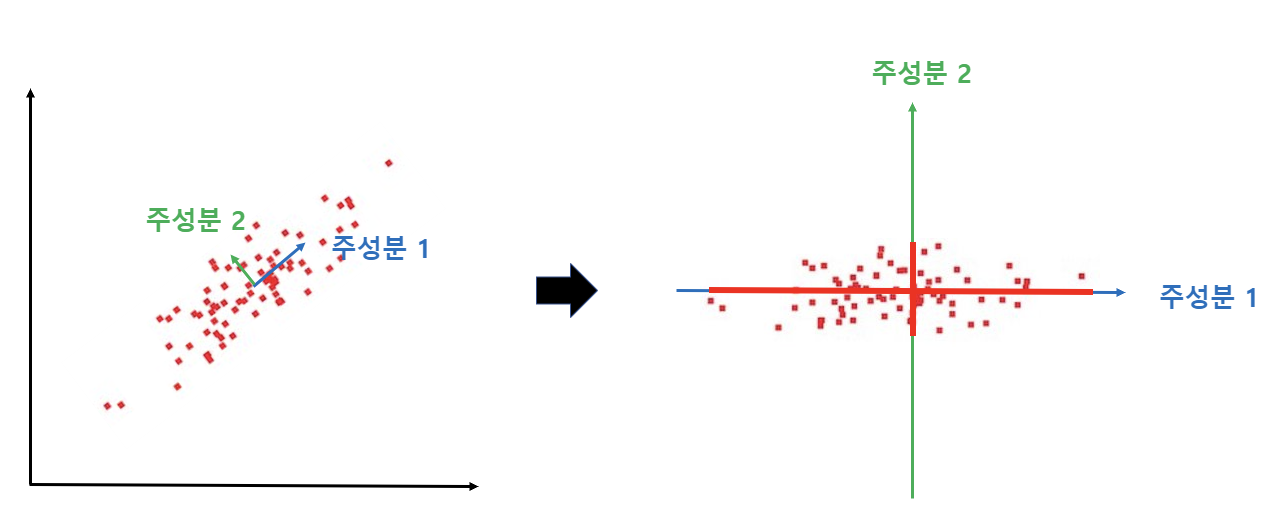
🧩 위 그림은 PCA(주성분분석) 기법을 통해 데이터 축소를 실시한 결과
- 데이터를 하나의 독립변수의 축으로 사영하였을 때 발생했던 문제가 나타나지 않음
- 새롭게 찾은 '주성분1(PC1)' 축에 데이터를 사영시켰을 때, 데이터의 원래 분포가 잘 설명됨을 위 그림을 통해 확인 가능
- 즉, 기존 데이터의 정보 손실을 최소화하여 1차원으로의 데이터 축소가 가능
📘 주성분 분석(PCA) 원리
🧩 사람들의 키와 몸무게에 대한 정보가 담겨있는 아래 2차원 데이터를 1차원으로 축소한다고 생각해보자
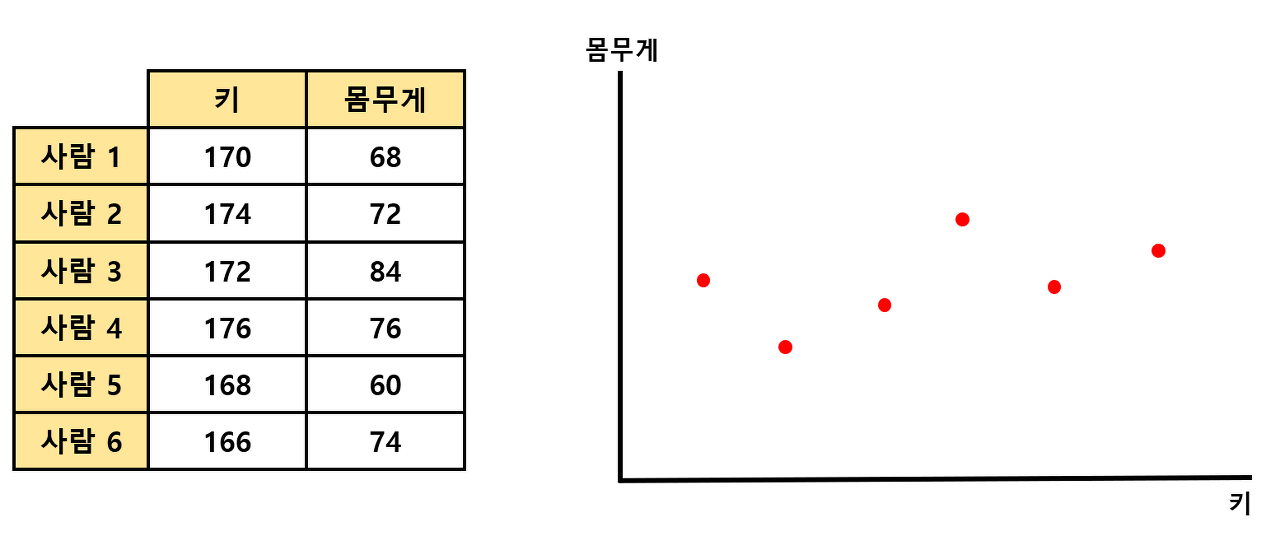
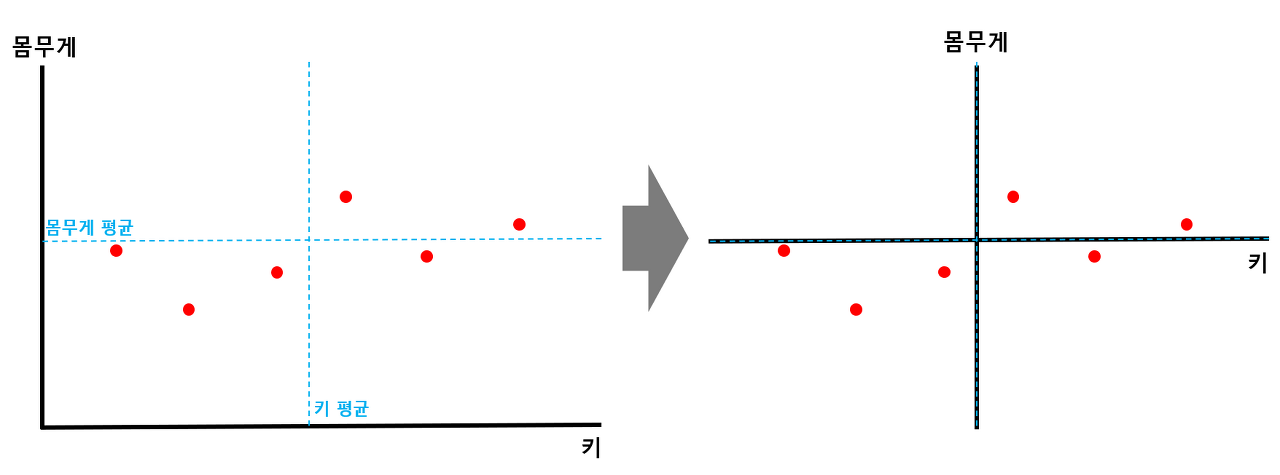
STEP#1 ) 각 축에 대한 평균값을 구한 뒤, 해당 점이 원점이 되도록 shift 해준다
- 데이터의 x축, y축에 대한 평균값을 구해준 뒤, 각 평균값에 해당하는 점들의 교차점이 원점이 되도록 전체 데이터를 shift 해줌
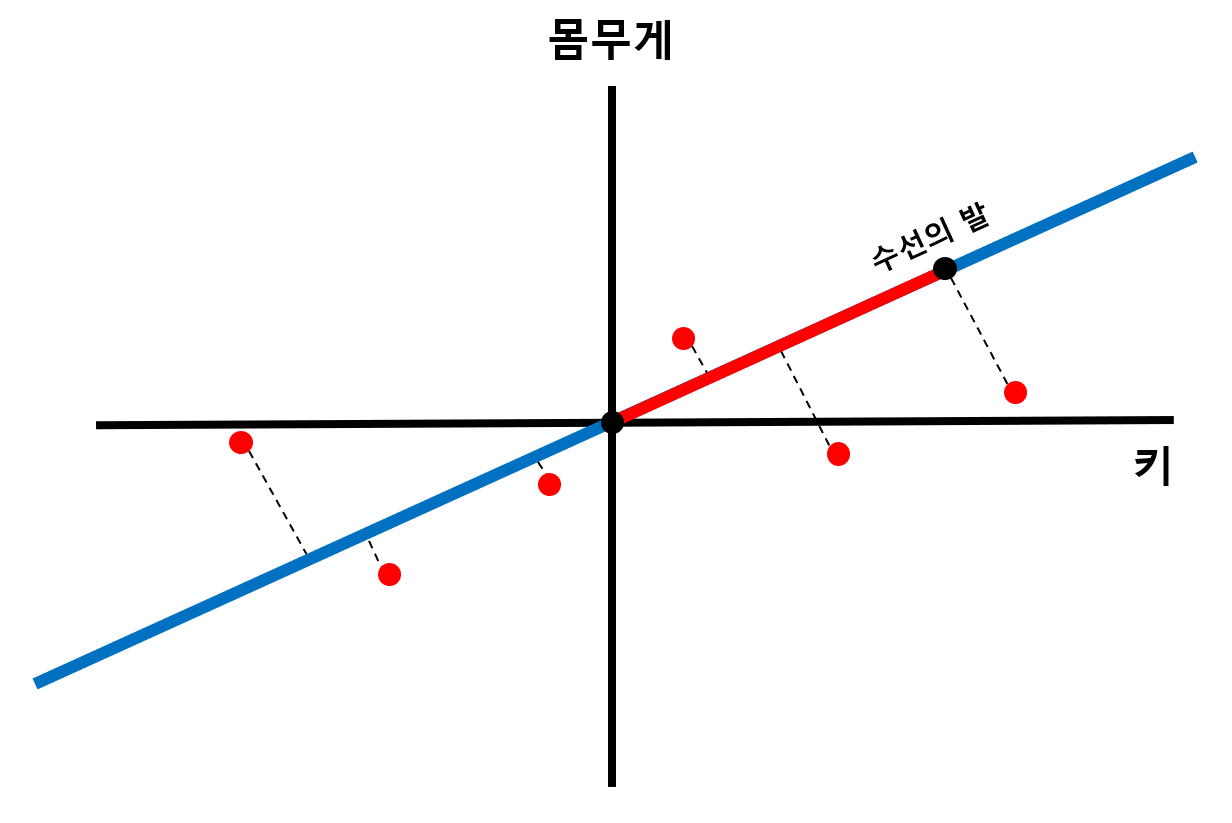
STEP#2) 데이터에서 원점을 지나는 직선에 수선의 발을 내려, 해당 길이가 최대가 되는 직선을 찾는다
- 위 그림과 같이 모든 데이터에서 원점을 지나는 직선에 수선의 발을 내리면, 원점으로부터 수선의 발까지의 거리를 구할 수 있음
- 원점을 지나는 직선의 기울기가 변함에 따라 원점으로부터 수선의 발까지의 거리들 또한 변화
- 이 거리의 제곱들의 합(Sum of Squares)이 최대가 되는 직선을 찾는다
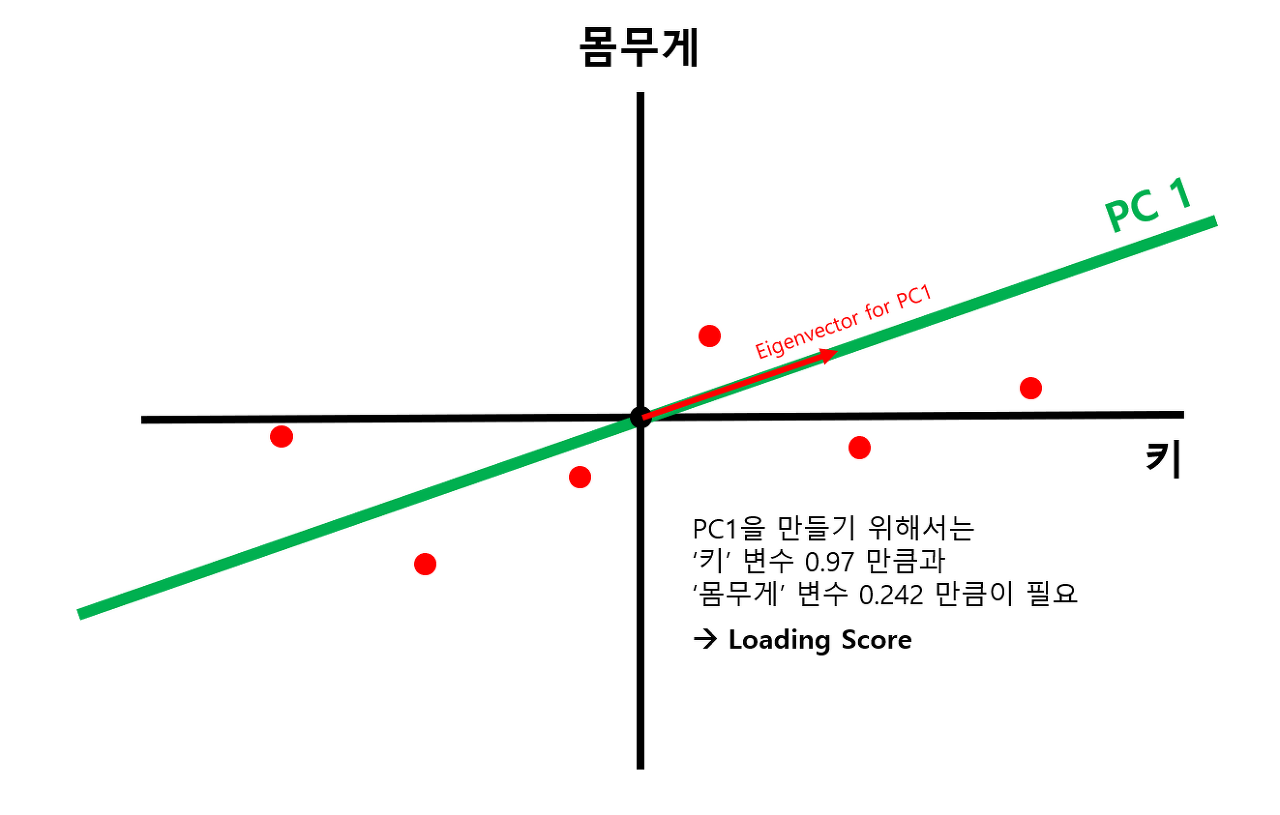
STEP#3) 찾은 직선을 PC1으로 설정하고, loading score를 구한다
- 위 그림의 PC1 직선은 Sum of Squares가 최대가 되는 최적의 직선을 찾은 결과에 해당
- PC1과 방향이 같은 벡터를 'PC1의 고유벡터(Eigenvector)'로 정의
- PC1의 고유벡터의 x축 거리와 y축 거리의 비율을 'Loading Score'로 정의
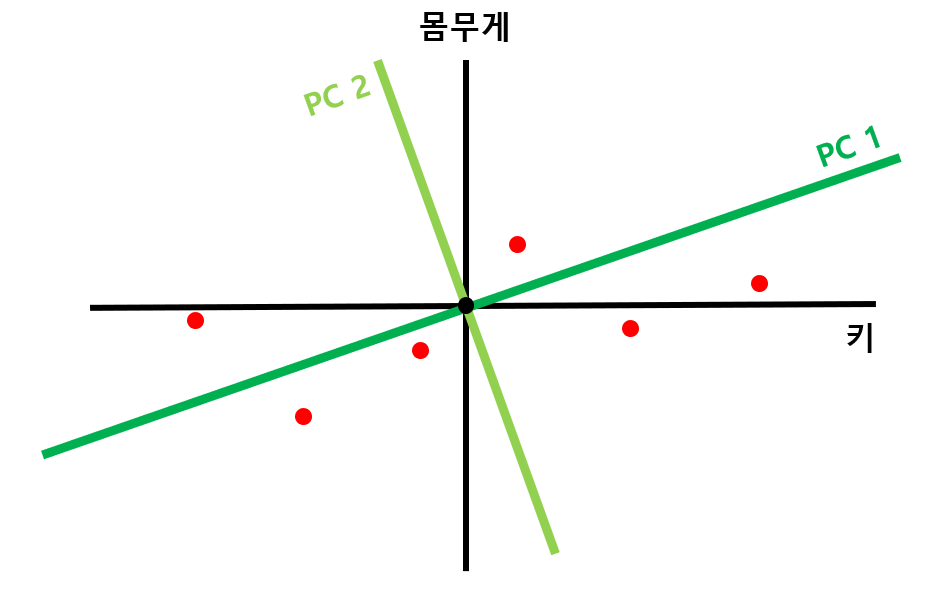
STEP#4) PC1에 직교하는 직선을 PC2로 잡는다
- 2차원 데이터를 예시로 들었으므로, PC1에 직교하는 직선이 유일하지만, 만약 3차원일 경우 PC1에 직교하는 직선이 평면으로 나타남
- N차원 데이터에는 N개의 PC 직선이 나타남
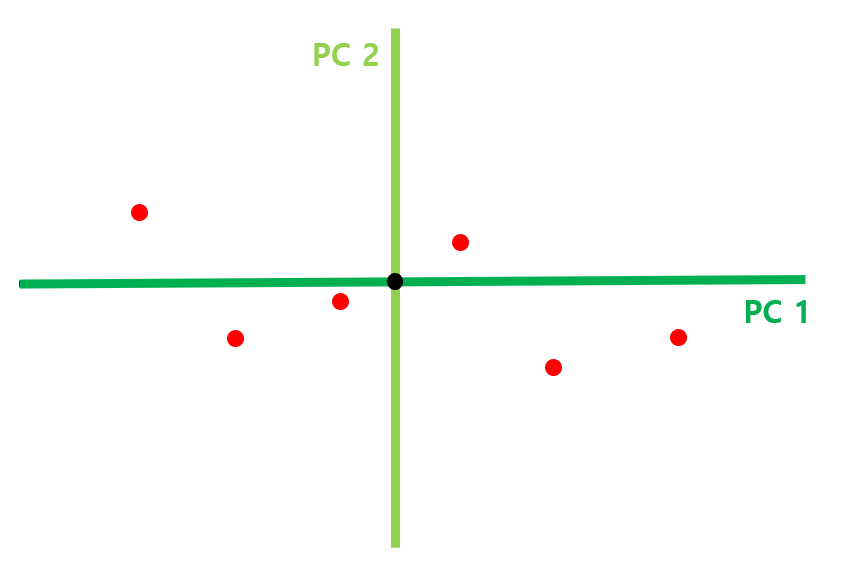
STEP#5) PC1과 PC2를 축으로 하여 회전시킨 뒤, scree plot 생성한다
- 위 그림은 앞서 구한 PC1과 PC2 직선을 각각 x축, y축이 되도록 데이터를 회전시킨 결과에 해당
- scree plot을 통해 각 PC 축이 전체 데이터를 얼마나 잘 표현하고 있는지 그 기여율을 알 수 있음
- 만약 PC1과 PC2의 기여율이 각각 89%, 11%라고 할 때, 89% 정도의 특징만으로도 해당 데이터를 잘 나타낼 수 있을 것이라고 판단되면, PC2 축을 제거하고 PC1 축만을 가지고 1차원으로 나타낼 수 있음
STEP#6) PCA 결과
- STEP#1 ~ STEP#5의 과정을 통해 2차원의 데이터가 위와 같이 1차원으로 축소
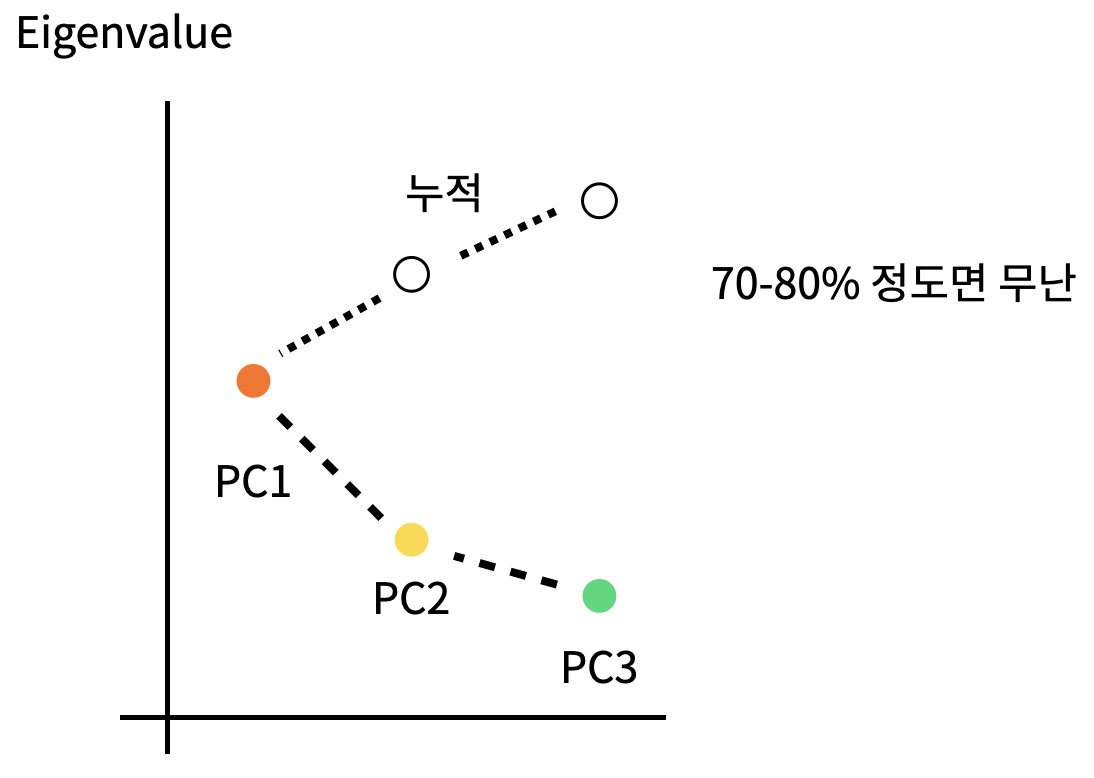
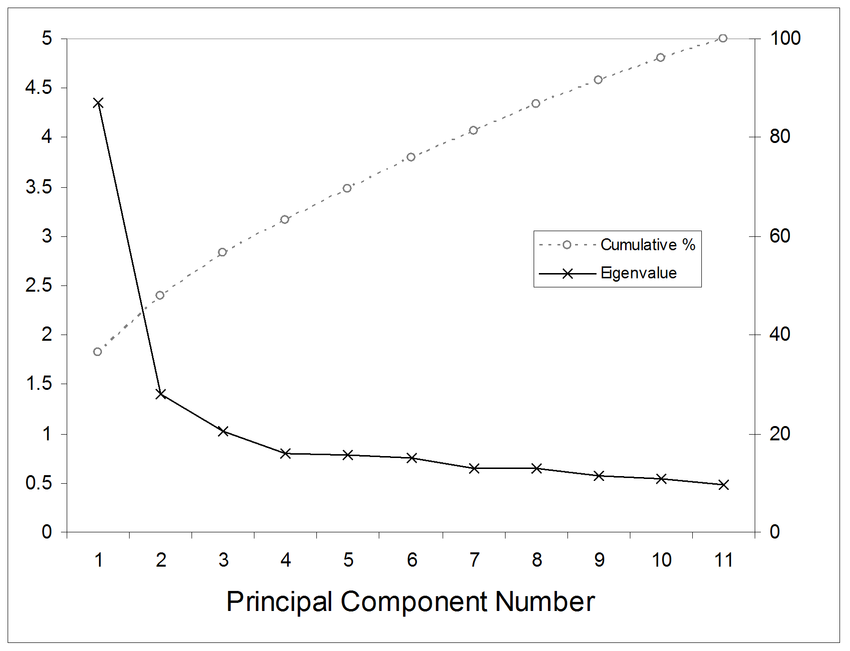
📌 Scree Plot
- PCA 실시 후, 주성분의 수를 결정하기 위해 활용하는 Plot
- x축은 주성분, y축은 해당 주성분의 고유값(Eigenvalue)을 의미
- 일반적으로 그래프가 완만해지는 지점까지의 주성분을 활용
🧩 원리를 쉽게 이해하기 위해 2차원 데이터를 1차원으로 축소하는 과정을 예시로 들었으나 실제 고차원의 데이터를 축소하는 과정은 다음과 같음
STEP#1) N차원의 데이터로부터 공분산 행렬(Covariance Matrix)을 생성
STEP#2) 생성된 공분산 행렬에서 N개의 고유값(Eigenvalue), 고유벡터(Eigenvector)를 찾음
STEP#3) 찾은 고유벡터를 고유값이 큰 순서대로 정렬
STEP#4) 원하는 차원 개수만큼의 고유벡터만 남기고 나머지는 제거
STEP#5) 남은 고유벡터를 축으로 하여 데이터 차원 축소
💻 코드 예시
(1) 주성분 분석 실시
from sklearn import datasets
from sklearn.decomposition import PCA
iris = datasets.load_iris() # 예시 데이터 셋으로 iris 사용
X = iris.data
y = iris.target
pca = PCA(n_components=4)
pca_fitted = pca.fit(X) # PCA는 Unsupervised Learning Algorithm
print(f'{pca_fitted.components_ = }') # 각 고유벡터(Eigenvector)의 x, y축 성분
print(f'{pca_fitted.explained_variance_ratio_ = }') # 각 고유 벡터가 설명할 수 있는 분산 비율(기여율)
X_pca = pca_fitted.transform(X) # 주성분 벡터로 데이터를 변환# result
pca_fitted.components_ = array([[ 0.36138659, -0.08452251, 0.85667061, 0.3582892 ],
[ 0.65658877, 0.73016143, -0.17337266, -0.07548102],
[-0.58202985, 0.59791083, 0.07623608, 0.54583143],
[-0.31548719, 0.3197231 , 0.47983899, -0.75365743]])
pca_fitted.explained_variance_ratio_ = array([0.92461872, 0.05306648, 0.01710261, 0.00521218])(2) Scree Plot 확인
import numpy as np
import matplotlib.pyplot as plt
def scree_plot(pca):
num_components = len(pca.explained_variance_ratio_)
ind = np.arange(num_components)
vals = pca.explained_variance_ratio_
ax = plt.subplot()
cumvals = np.cumsum(vals)
ax.bar(ind, vals, color = ['g', 'y', 'm', 'b']) # Eigenvalue bar plot
ax.plot(ind, cumvals, color = 'r') # Cumulative line plot
for i in range(num_components):
ax.annotate(r"%s" % ((str(vals[i]*100)[:3])), (ind[i], vals[i]), va = "bottom", ha = "center", fontsize = 13)
ax.set_xlabel("PC")
ax.set_ylabel("Variance")
plt.title('Scree Plot')
scree_plot(pca)# result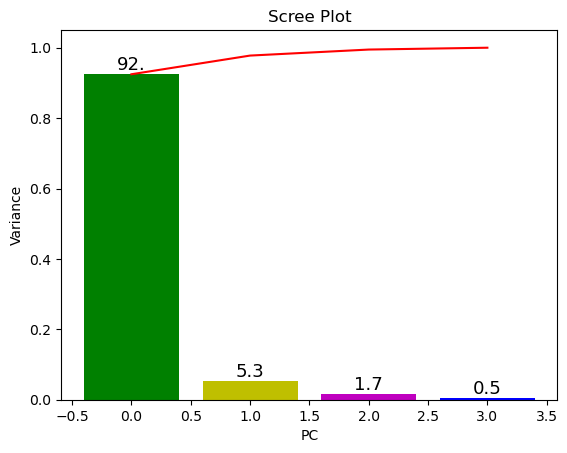
(3) 차원 축소 방향 결정
📌 위 Scree Plot을 토대로 차원 축소의 방향을 둘 중 하나로 결정 가능
1) 4차원에서 1차원으로 차원 축소, 기여율 92%
2) 4차원에서 2차원으로 차원 축소, 기여율 97.3%
이는 주어진 문제 상황에 따라 적절한 방법을 선택하여 실시하면 됨!
import pandas as pd
import seaborn as sns
pca_r = PCA(n_components=2)
pca_r_fitted = pca_r.fit(X)
X_pca_r = pca_r_fitted.transform(X)
df_pca_r = pd.DataFrame(X_pca_r, columns=['PC1', 'PC2'])
y = pd.Series(y).replace({0:'setosa', 1:'versicolor', 2:'virginica'})
sns.scatterplot(df_pca_r, x='PC1', y='PC2', hue=y, style=y, palette='Set1').set(title='PCA of IRIS dataset');# result📚 선형판별 분석(Linear Discriminant Analysis, LDA)
📙 선형판별 분석(LDA)이란?
👉 분류(Classification) 모형을 통한 차원 축소 기법
👉 클래스 내부(within-class) 분산이 최소가 되는, 클래스 중심 간(between-class) 거리가 최대가 되는 벡터를 찾아 데이터를 투영하여 차원을 축소하는 기법
📗 목적
👉 데이터를 특정 한 축에 사영한 후 두 클래스(범주)를 잘 구분할 수 있는 직선을 찾는 것이 목적
👉 가능한 클래스 간의 분류 정보를 최대한 유지시키면서 차원을 축소시키기 위함
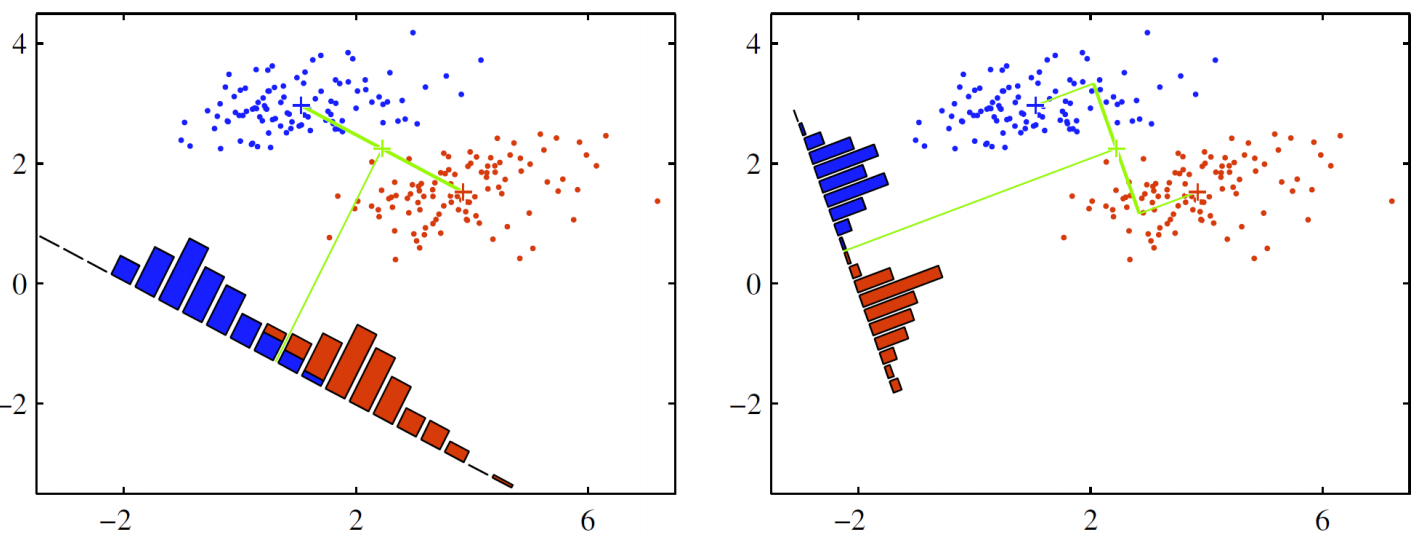
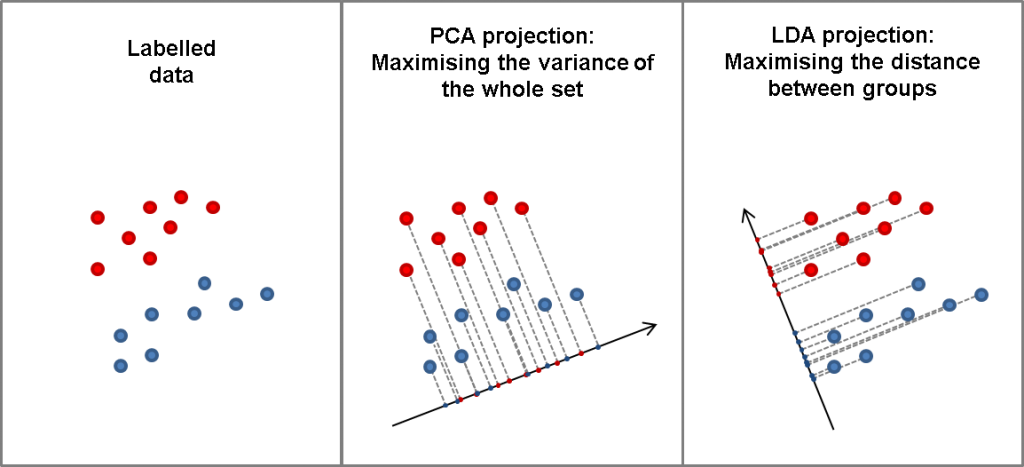
🧩 왼쪽과 오른쪽 축 중에 분류가 더 잘 되었다고 판단할 수 있는 축은?
- 빨간색 점과 파란색 점을 분류하는 것을 목표로 한다고 하자
- 왼쪽의 경우 축소 결과, 빨간색 점과 파란색 점이 서로 뒤섞여 있는 부분이 존재
- 오른쪽의 경우는 축소 결과, 두 점이 서로 뒤섞이지 않고 명확하게 구분되고 있음을 확인 가능
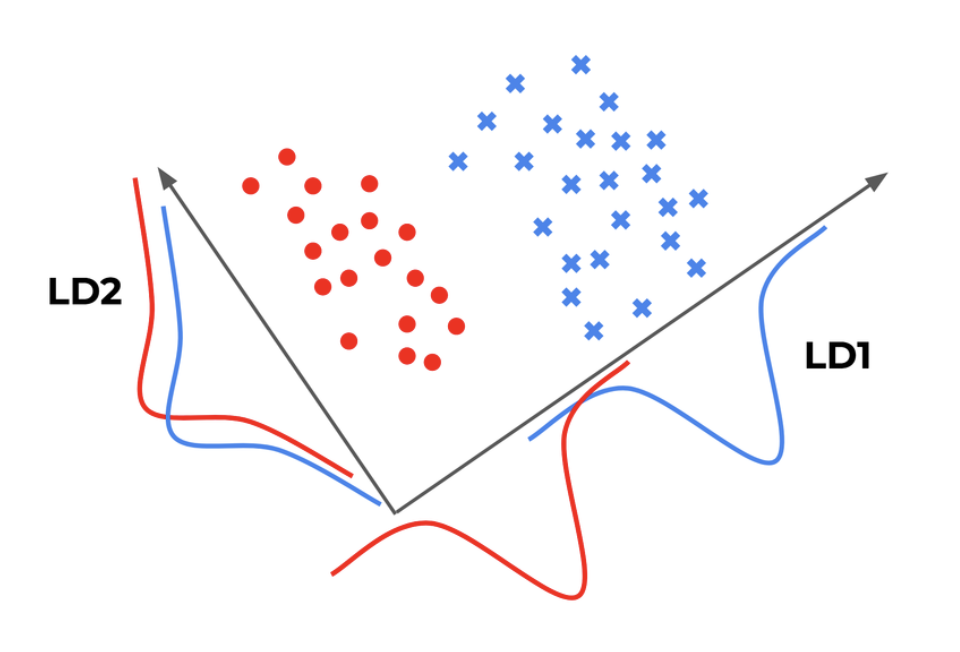
🧩 그럼 두 클래스를 잘 구분할 수 있는 직선은 어떤 성질을 가져야 할까?
- 특정 축으로 사영 후 두 클래스 간의 중심(평균)이 서로 멀리 떨어져 있고, 클래스 내의 점들의 분산이 작아야 함
- 왼쪽의 경우 축소 결과, 두 클래스 간의 중심이 가깝고 분산은 커서 데이터가 제대로 분류되지 않고 있음을 확인 가능
- 그러나 오른쪽의 경우는 축소 결과, 두 클래스 간 중심이 멀고 클래스 내 분산이 작아 분류가 비교적 잘 이루어짐을 확인 가능
선형판별분석(LDA)는 이러한 직선을 찾도록 해주는 데이터 축소 알고리즘!
💻 코드 예시
import pandas as pd
import seaborn as sns
from sklearn import datasets
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
iris = datasets.load_iris()
X = iris.data
y = iris.target
lda = LinearDiscriminantAnalysis(n_components=2) # 4차원에서 2차원으로 축소
lda_fitted = lda.fit(X, y) # LDA는 Supervised Learning Algorithm
print(f'{lda_fitted.coef_=}') # LDA의 고유벡터 성분
print(f'{lda_fitted.explained_variance_ratio_=}') # LDA의 분산에 대한 설명력(기여율)
X_lda = lda_fitted.transform(X)
df_lda = pd.DataFrame(X_lda, columns=['LD1', 'LD2'])
y = pd.Series(y).replace({0:'setosa', 1:'versicolor', 2:'virginica'})
sns.scatterplot(df_lda, x='LD1', y='LD2', hue=y, style=y, palette='Set1').set(title='LDA of IRIS dataset');# result
lda_fitted.coef_=array([[ 6.31475846, 12.13931718, -16.94642465, -20.77005459],
[ -1.53119919, -4.37604348, 4.69566531, 3.06258539],
[ -4.78355927, -7.7632737 , 12.25075935, 17.7074692 ]])
lda_fitted.explained_variance_ratio_=array([0.9912126, 0.0087874])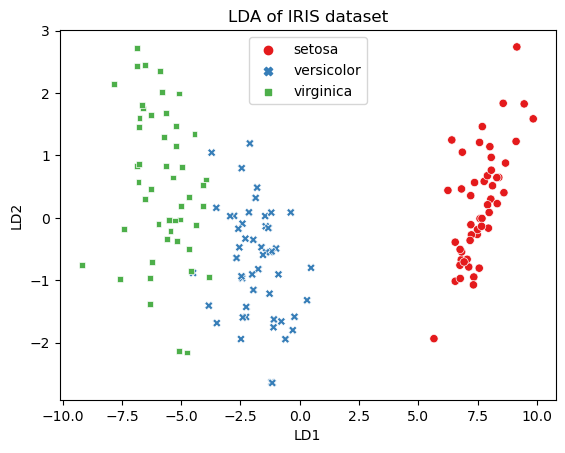
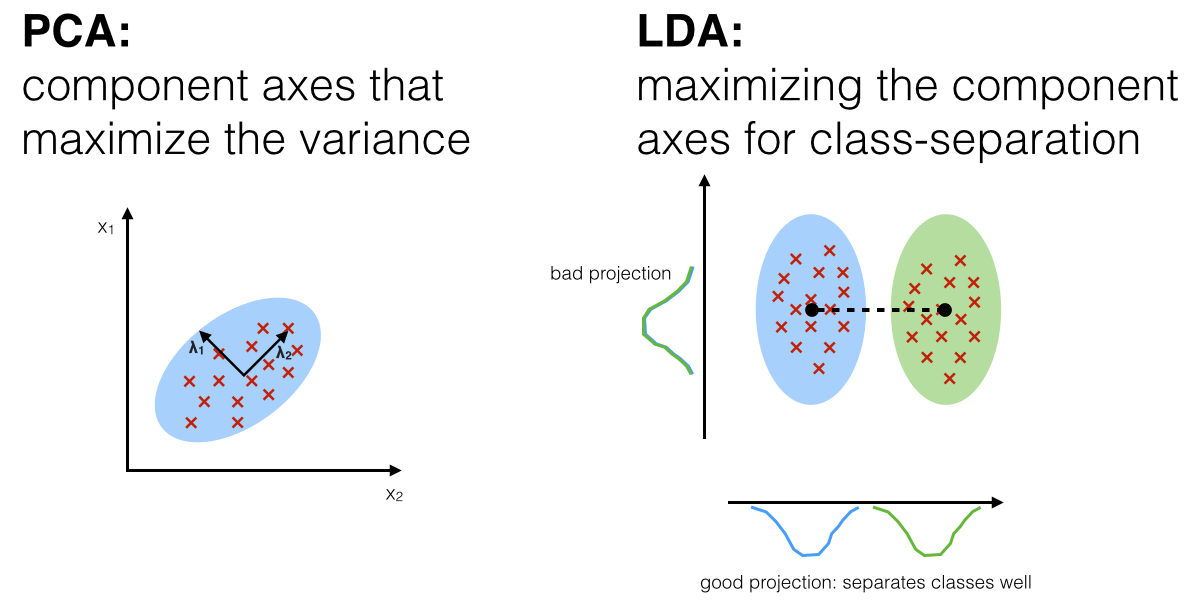
💡 주성분 분석(PCA) vs 선형판별 분석(LDA)
⭐ 공통점
👉 입력 데이터 세트를 저차원 공간에 투영해 차원을 축소하는 기법
🔥 차이점
✅ 주성분 분석(PCA)
- 비지도학습(Unsupervised Learing) 알고리즘
- 데이터를 투영시켰을 때, 최대의 분산을 갖는 고유벡터(Eigenvector)를 찾음
- 분산이 작은 고유벡터들을 제거해 줌으로써 데이터의 차원을 감소시키는 기법
- 데이터의 정보 손실을 최소화 하여 최적의 표현을 할 수 있도록 초점을 맞추어 데이터를 축소하는 기법
- 데이터의 클래스의 차이가 평균보다 분산의 차이에 있을 때, PCA는 LDA보다 뛰어난 성능을 보여줌
✅ 선형판별 분석(LDA)
- 지도학습(Supervised Learning) 알고리즘
- 입력 데이터의 결정 값 클래스를 가장 잘 구분할 수 있는 새로운 축을 찾음
- 서로 다른 클래스의 분리를 위해 클래스 평균 간 거리를 최대화하고, 클래스 내 분산을 최소화하는 기법
- 데이터의 클래스의 차이가 분산보다 평균의 차이에 있을 때, LDA는 PCA보다 뛰어난 성능을 보여줌
🙏 Reference
https://backenddeveloper.tistory.com/183
https://bioinformaticsandme.tistory.com/188
https://ssungkang.tistory.com/entry/%EC%9D%B8%EA%B3%B5%EC%A7%80%EB%8A%A5-PCA-1-Principle-Component-Analysis-%EB%9E%80?category=324327
https://ddongwon.tistory.com/114