[PP] Data Cleansing(2)_이상치(Outliers)

양승웅·2023년 11월 21일

PreProcessing

목록 보기

4/9

📢 개요

이상치는 데이터를 수집, 입력, 측정 등의 과정 상에서 발생하는 오류로 인하여 발생할 수 있으며 이외에도 여러 다양한 원인으로 인하여 발생할 수 있다. 이러한 이상치는 통계 분석 결과에 영향을 미쳐 연구의 목적을 훼손시킬 수 있으며 혹은 Machine Learning, Deep Learning 등의 데이터 분석 모델링 결과에 왜곡 또는 편향된 결과를 초래할 수 있다. 따라서 반드시 정제 과정을 거쳐주어야 하는데 이번 포스트에서는 이상치가 발생하는 원인과 유형들, 검출방법, 처리방법 등에 대해 정리해보고자 한다.

✏️ 이상치(Outlier)란?

👉 분석자료에서 가정한 통계적 분포로부터 크게 벗어나 있는 극단적인 관측값
👉 이상치는 분산을 과도하게 증가시켜 검정력, 예측력 등 통계적 특성을 왜곡 또는 저하시킬 수 있음
👉 전체 데이터 수가 많을 경우에는 이상치의 영향이 감소

⭐ 의사결정을 위해 필요한 데이터를 분석 혹은 모델링하는 경우, 이상치가 의사결정에 큰 영향을 미칠 수 있기 때문에 데이터 전처리 과정에서 적절한 이상치 처리는 필수적!

📌 이상치(Outlier)와 혼동할 수 있는 개념들은 아래 포스트 참고!
Anomaly_Detection

❓ 발생 원인

1) 비자연적 이상치 (Non-Natural Outlier)

✅ 입력 실수 (Data Entry Error)
👉 데이터 수집 과정에서 발생하는 에러
👉 입력의 실수 등을 지칭

✅ 측정 오류 (Measurement Error)
👉 데이터의 측정 중에 발생하는 에러
👉 측정기 고장(이상 작동) 등을 지칭

✅ 실험 오류 (Experimental Error)
👉 실험과정 중 발생하는 에러
👉 실험 환경에서 야기된 모든 문제점 지칭

✅ 의도적 이상치 (Intentional Outlier)
👉 자기 보고 측정(Self-Reported Measure)에서 발생하는 에러
👉 자기 보고 측정에서 발생하는 이상치(의도가 포함된)를 지칭
🧩 예) 설문조사 시 10대들은 알코올 섭취량을 일부러 낮게 적음

✅ 자료 처리 오류 (Data Processing Error)
👉 데이터 분석 시, 분석 전의 전처리 과정에서 발생하는 에러

✅ 표본 오류 (Sampling Error)
👉 모집단에서 표본을 추출하는 과정에서 발생하는 에러
👉 편향(bias)이 발생하는 경우를 지칭
🧩 예) 농구선수의 키를 조사하기 위해 sampling 했는데 농구선수 이름이 포함됨

2) 자연적 이상치 (Natural Outlier)

👉 말 그대로 자연적으로 발생한 이상치
👉 위 오류들을 제외한 모든 이상치들에 해당
🧩 예) 어느 회사 직원들의 월급 중 임원들의 월급은 일반 사원들의 월급과 큰 차이가 있음

🔎 탐색

이상치 검출은 개별 데이터 관찰을 통한 검출 방법, 기초통계량을 활용한 통계적 기법, 시각화 방법 그리고 머신러닝 모델 활용 총 4가지의 방법으로 검출 가능
변수가 단변량인지 다변량인지, 모수적인지 비모수적인지 등을 고려하여 다양한 방식으로 이상치를 탐지 가능

❗ 탐색 과정시 주의사항

가면효과 (Masking Effect)

이상치 탐색 과정에 일부 극단치에 의해 이상치로 분류되어야 하는 값들이 정상 범주값으로 정의되는 현상

수렁효과 (Swamping Effect)

정상 범주 값이 이상치와 근접하여 동일하게 이상치로 판별되는 현상

1. 통계적 방법

1.1 Z-Score (표준화 점수)

\boxed{{Z} = \frac{x - \mu}{\sigma}   \mu : 평균 \sigma : 표준편차}

👉 평균 μ, 표준편차 σ의 정규분포를 따르는 관측치들이 데이터의 중심에서 얼마나 떨어져 있는지 파악하여 이상치 검출
👉 ∣Z∣ > 3이면 이상치로 간주함
👉 변수가 하나인 단변량 데이터에 적절한 탐색방법

🌟 장점

일관된 비율로 이상치를 탐색 가능

🔥 단점

데이터가 정규분포를 따르는 데이터여야 함
평균과 표준편차에 의존하므로 산출 과정에서 이상치의 영향을 받을 수 있음

💻 코드 예시

import pandas as pd
from scipy.stats import t, zscore

df = pd.DataFrame({'x':[4, 5, 6, 2, 12, 4, 3, 1, 2, 3, 23, 5, 3]})

z = zscore(df.x)
print('Z-score Outliers:', df.x[(z<-3)|(z>3)].values)

1.2 Modified Z-Score

\boxed{{Modified Z} = \frac{x - \widetilde{x}}{MAD}  \widetilde{x} : 중앙값}

👉 Z-Score 방법의 문제점을 보완하기 위해 중앙값과 Median Absolute Deviation(MAD)를 이용하는 방법
👉 평균, 표준편차 대신 중앙값을 이용하여 이상치가 산출과정에 미치는 영향 최소화

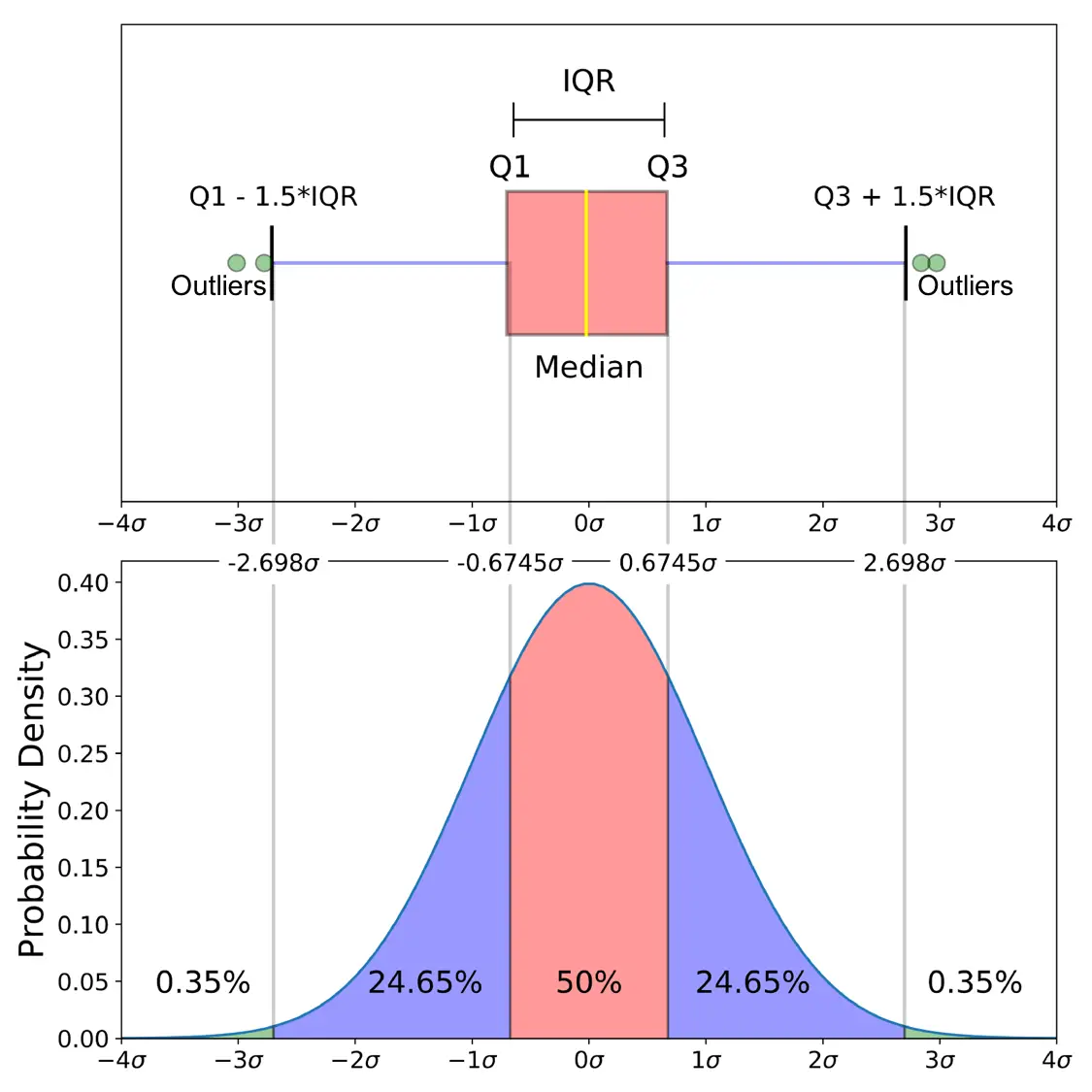
1.3 IQR (Interquantile Range / 사분위수 범위)

👉 IQR이란 제3사분위수 Q3(상위 75%)과 제1사분위수 Q1(하위 25%)의 차이로 정의
👉 일반적인 데이터가 가질 수 있는 최소값(Q1-1.5IQR)보다 작거나 최댓값(Q3+1.5IQR)보다 큰 관측치를 이상치로 검출
👉 일반적으로 Boxplot을 이용할 때 사용하는 방법
👉 변수가 하나인 단변량 데이터에 적절한 탐색방법

🌟 장점

데이터 수가 적은 경우에도 적용이 가능
산출 과정이 쉬워 일반적으로 많이 사용됨

🔥 단점

이상치 검출을 위한 상수는 자료의 분포 등을 고려하여 경험적인 판단으로 결정해야 함

💻 코드 예시

import pandas as pd
import seaborn as sns

df = pd.DataFrame({'x':[4, 5, 6, 2, 12, 4, 3, 1, 2, 3, 23, 5, 3]})
sns.boxplot(df.x)

#1 pandas 이용
Q1 = df.x.quantile(0.25)
Q3 = df.x.quantile(0.75)
IQR = Q3 - Q1
ols = df.x[(df.x < (Q1 - 1.5*IQR)) | (df.x > (Q3 + 1.5*IQR))]
print('IQR Outliers 1:', ols.values)

#2 scikit_posthocs 이용
import scikit_posthocs as sp
print('IQR Outliers 2:', sp.outliers_iqr(df.x, ret = 'outliers'))

1.4 Grubb's t-test

\boxed{{G} = \frac{max_{i=1,2,{...},N} ∣Y_i - \overline{Y}∣}{S}   \overline{Y} : 표본평균 S : 표본분산}

👉 정규분포를 만족하는 단변량 데이터에서 이상치를 검정하는 방법
👉 t-분포에 근거한 임계치를 산출하여 검정통계량이 임계치보다 큰 경우 이상치로 결정
⭐ Hypothesis

귀무가설 $H_{0}$ : 데이터 셋에 이상치가 없다
대립가설 $H_{1}$ : 데이터 셋에 정확히 하나의 이상치가 존재한다

🌟 장점

직관적이고 구현 과정이 간단함

🔥 단점

한 번에 하나의 이상치만을 검출할 수 있음
특이치의 개수를 정확히 지정해야하며 그렇지 않을 경우 결과가 왜곡될 수 있음

💻 코드 예시

import scikit_posthocs as sp

inliers = sp.outliers_grubbs(df.x)
outliers = df.x[(df.x<inliers.min())|(df.x>inliers.max())]

print('Grubb\'s Outliers:', outliers.values)

1.5 Generalized ESD (Extreme Studentized Deviate) test

\boxed{{R_{i}} = \frac{max_{i=1,2,{...},r} ∣x_i - \overline{x}∣}{S}   \overline{x} : 표본평균 S : 표본분산}

👉 ESD test를 일반화한 방법으로 단변량 데이터에서 여러 개의 이상치에 대한 검정이 가능한 방법
👉 검정통계량은 내림차순으로 정렬하여 각 관측치별로 산출되며, 검정통계량이 t-분포에 근거한 임계치보다 크면 해당 관측치를 이상치로 검출
⭐ Hypothesis

귀무가설 $H_{0}$ : 데이터 셋에 이상치가 없다
대립가설 $H_{1}$ : 데이터 셋에 이상치가 최대 r개 존재한다

💻 코드 예시

import scikit_posthocs as sp

# outliers_gesd는 test summary를 제공
print(sp.outliers_gesd(df.x, outliers = 3, report = True))

inliers = sp.outliers_gesd(df.x)
outliers = df.x[(df.x<inliers.min())|(df.x>inliers.max())]

print('G-ESD Outliers:', outliers.values)

1.6 Chi-Square test (카이제곱 검정)

👉 데이터가 정규분포를 만족하나, 자료 수가 적은 경우 이상값을 검정하는 방법
👉 검정통계량은 자유도가 1인 카이제곱 분포를 따르는 통계량이며, 임계치보다 클 경우 한개 이상의 이상치가 있다고 판단함

1.7 Dixon's Q-test

👉 오름차순으로 정렬된 데이터에서 범위에 대한 관측치 간 차이에 대한 비율을 활용하여 이상치 여부를 검정하는 방법
👉 데이터가 30개 미만일 경우 적절한 방법

\boxed{{Q} = \frac{gap}{range}}

gap : 이상치로 추정되는 값, 그리고 그 값과 가장 가까운 숫자간의 절댓값 차이
range : 전체 데이터의 (최대값 - 최소값) 차이

👉 위와 같이 계산된 Q값이 table의 Q값보다 클 경우 이상치로 추정되는 값이 이상치가 맞다는 결론을 내리는 방식으로 검출

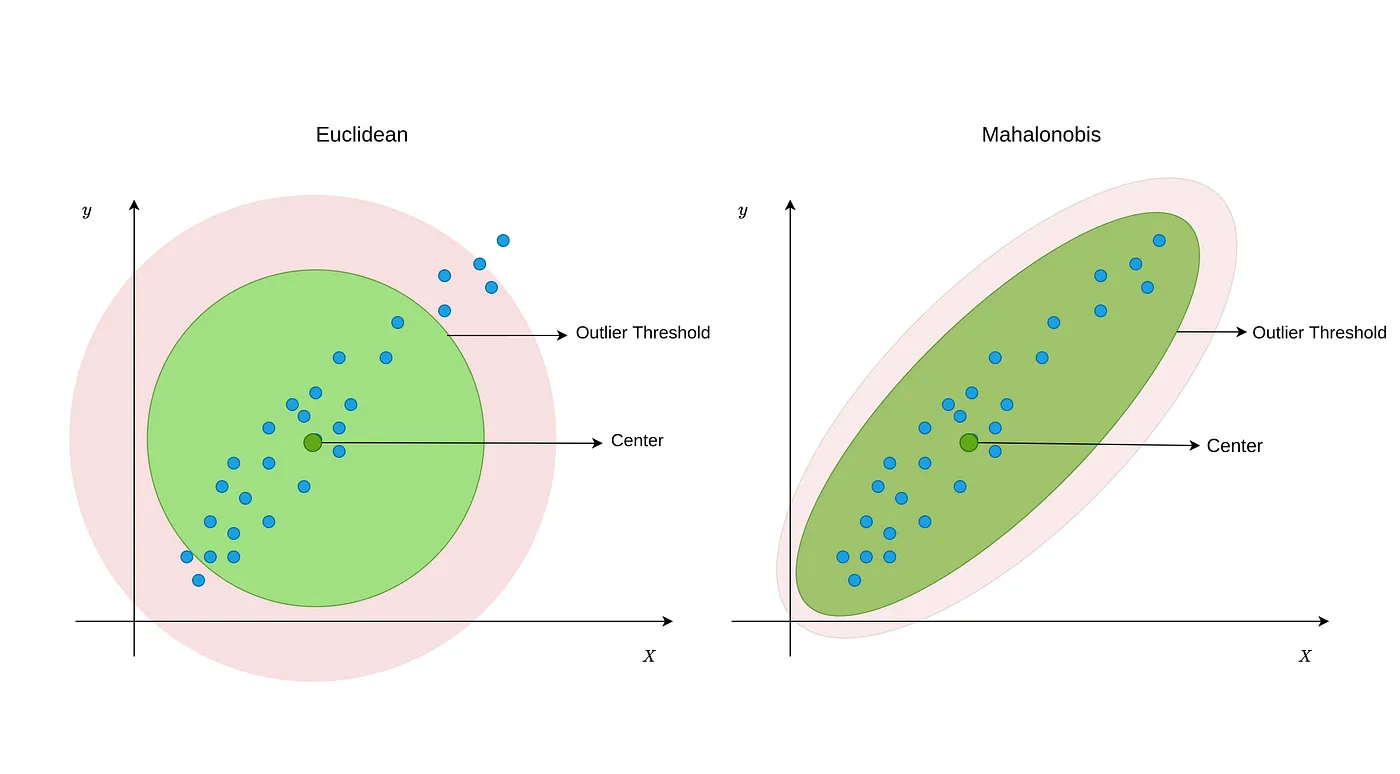
1.8 Mahalanobis Distance (마할라노비스 거리)

👉 데이터의 분산을 고려한 거리의 측도이며, 관측치가 평균으로부터 벗어난 정도를 분산을 고려하여 측정하는 통계량
👉 마할라노비스 거리를 이용하여 평균으로부터 벗어난 이상치를 검출
👉 상관관계가 있는 2개 이상의 다변량 데이터에서의 이상치 검출 기법
👉 데이터의 분포에 따라 중심을 중앙값으로도 설정 가능

🌟 장점

관측치 사이의 거리 뿐만 아니라 분포도 함께 고려함

🔥 단점

중심점을 평균으로 계산할 경우 이상치의 영향을 받아 왜곡 우려
산출과정이 복잡하고 통계적 가정 사항이 많음

💻 코드 예시

from sklearn.covariance import EllipticEnvelope

md = EllipticEnvelope(contamination=outliers_fraction).fit(df)

# result (Example)
Mahalanobis Distance: [ 1  1  1  1  1 -1  1  1  1  1  1  1  1  1  1  1 -1  1  1  1]

2. Model-based Method

2.1 LOF(Local Outlier Factor)

👉 관측치 주변의 밀도와 관측치에 근접한 이웃들의 주변 밀도의 상대적인 비교를 통해 이상치를 탐색하는 방법
👉 데이터 전체를 고려하는 것이 아닌, 해당 관측치의 주변 데이터(neighbor)를 이용하여 국소적인 관점에서 이상치를 파악하고자 하는 원리
👉 주변 데이터를 몇 개까지 고려할 것인지를 나타내는 Hyper-parameter k 결정 필요

\boxed{\frac{\sum_{o\in\N_{k}(p)} \frac{lrd_{k}(o)}{lrd_{k}(p)}}{|N_{k}(p)|}  LOF_{k}(p) : 관측치 p의 이상치 정도}

👉 관측치 p의 밀도 $lrd_k(p)$ 가 작을수록, 이웃 o의 밀도 $lrd_k(o)$ 가 클수록 LOF는 큼
$\implies$ '이상치의 정도가 크다'

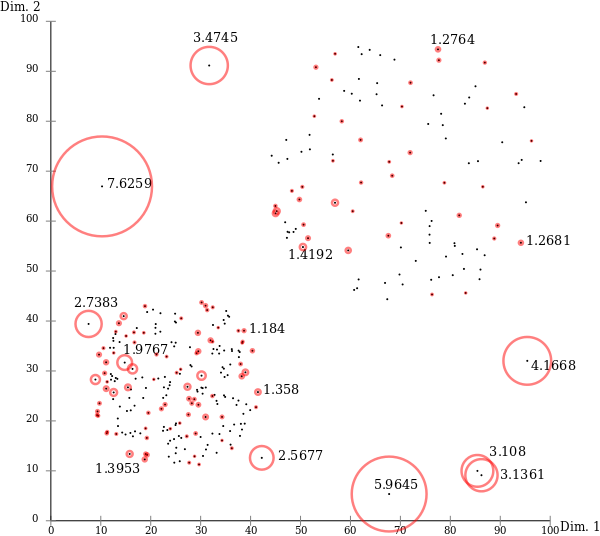
LOF < 1 : 주변 관측치에 비해 밀도가 높은 분포
LOF ≒ 1 : 주변 관측치와 비슷한 분포
LOF > 1 : 주변 관측치에 비해 밀도가 낮은 분포, 크면 클수록 이상치 정도가 큼.

🌟 장점

구조가 간단하여 효과적으로 검출 가능
통계적 가정사항이 요구되지 않음

🔥 단점

k번째 근방의 데이터를 찾아내는 과정에서 크기가 큰 데이터의 경우 계산량이 많아져 사용이 어려움

💻 코드 예시

from sklearn.neighbors import LocalOutlierFactor

lof = LocalOutlierFactor(n_neighbors=5, contamination=outliers_fraction)

inliers = lof.fit_predict(df)
print('Local Outlier Factor:', inliers)

# result (Example)
Local Outlier Factor: [-1  1  1  1  1 -1  1  1  1  1  1  1  1  1  1  1  1  1  1  1]

2.2 iForest(Isolation Forest)

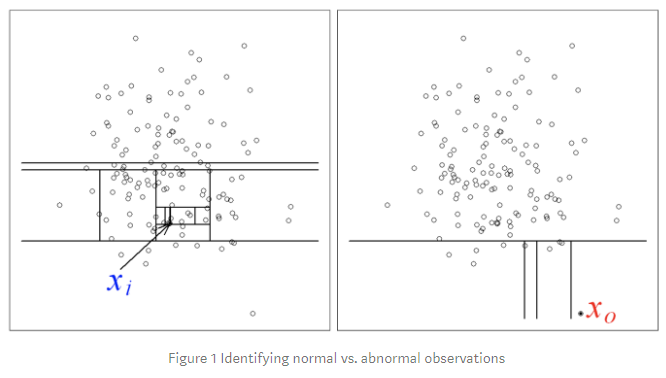
👉 관측치 사이의 거리 또는 밀도에 의존하지 않고 여러 의사결정 나무(Decision Tree)를 종합한 앙상블 기반의 이상치 탐지 방법

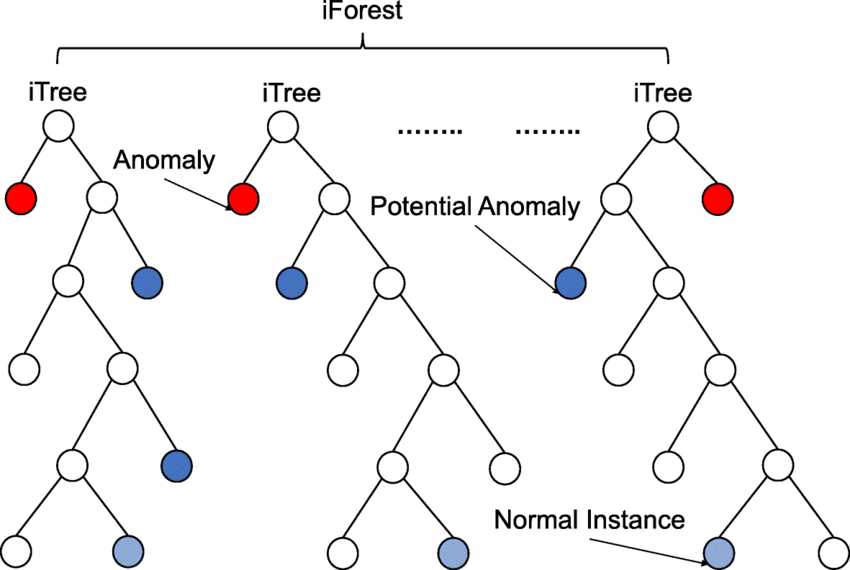
👉 무작위로 데이터를 Split 해가면서 모든 관측치를 고립시키며 구현
👉 비정상 데이터의 경우 root의 가까운 거리에서 고립되며 정상 데이터의 경우 root와 먼 거리에서 고립
$\implies$ 적은 횟수로 Leaf node(의사결정 나무의 끝)에 도달하는 관측치일 수록 높은 확률로 이상치일 것으로 판단

📍 예시

정상 데이터( $x_{i})$ 를 분리하는 경우, 약 11번의 split 필요

이상치( $x_{0}$ )를 분리하는 경우, 약 4번의 split 필요

🌟 장점

변수가 많은 고차원 데이터에서도 효율적으로 작동
통계적 가정사항이 요구되지 않음

💻 코드 예시

from sklearn.ensemble import IsolationForest

iforest = IsolationForest(contamination=outliers_fraction).fit(df)

# result (Example)
Isolation Forest: [-1  1  1  1  1 -1  1  1  1  1  1  1  1  1  1  1  1  1  1  1]

2.3 DBSCAN(Density Based Spatial Clustering of Applications with Noise)

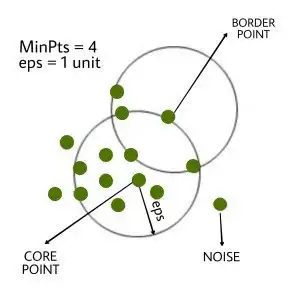
👉 데이터가 집중되어 있는 밀도에 초점을 두어 밀도가 높은 그룹을 군집화 하는 방식
👉 중심점을 기준으로 특정 반경 이내에 케이스가 n개 이상 있을 경우 하나의 군집을 형성하는 알고리즘
👉 중심으로부터 멀리 떨어진 데이터는 군집화 처리 되지 않으므로 어느 군집에도 속하지 못한 데이터를 이상치로 판단

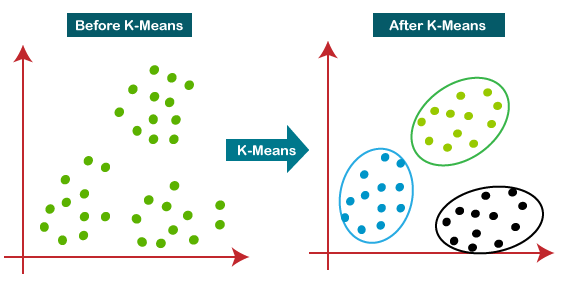
📌 K-means vs DBSCAN

K-means : 각각의 sample들을 k개의 centroid 중 가까운 군집으로 편성. 유사한 군집을 도출하기 위한 목적으로 사용.

DBSCAN : 밀도가 높은 부분을 군집화. 멀리 떨어진 데이터, 즉 이상치를 탐지하기 위한 목적으로 사용

💻 코드 예시

from sklearn.cluster import DBSCAN
dbscan = DBSCAN(eps = 0.5, metric = 'euclidean', min_samples = 5)
# eps : maximum distance between two samples for one to be considered as in the neighborhood of the other
# min_samples : number of samples in a neighborhood for a point to be considered as a core point
# metric : use when calculating distance between instances in a feature array

db = dbscan.fit_predict(data)
db

# result (Example)
array([ 0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,
        0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,
	    0,  0,  0,  0,  0,  0,  0, -1,  0,  0,  0,  0,  0,  0,  0,  0,  1,
    	1,  1,  1,  1,  1,  1, -1,  1,  1, -1,  1,  1,  1,  1,  1,  1,  1,
   	   -1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,
    	1,  1, -1,  1,  1,  1,  1,  1, -1,  1,  1,  1,  1, -1,  1,  1,  1,
    	1,  1,  1, -1, -1,  1, -1, -1,  1,  1,  1,  1,  1,  1,  1, -1, -1,
    	1,  1,  1, -1,  1,  1,  1,  1,  1,  1,  1,  1, -1,  1,  1, -1, -1,
    	1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1],
  		dtype=int64)

DBSCAN 모델을 통한 학습 후 예측 결과가 위와 같다고 할 때, 이는 데이터가 '0'과 '1' 총 2개의 군집으로 분류된 것임을 의미.
모델 기준에서 이상치로 파악된 데이터는 '-1'로 출력됨
DBSCAN 모델은 'eps'와 'min_samples'을 어떻게 설정하는지에 따라 이상치가 많아질 수도 적어질 수도 있으므로 상황에 맞게 적절히 조정해야 함

2.4 회귀진단 (Regression Diagnostics)

👉 회귀계수 추정 후 잔차(Residual)의 다양한 통계량을 사용하여 이상치를 탐색
👉 회귀분석에서는 이상치, 레버리지, 영향점을 구분하여 회귀진단 수행

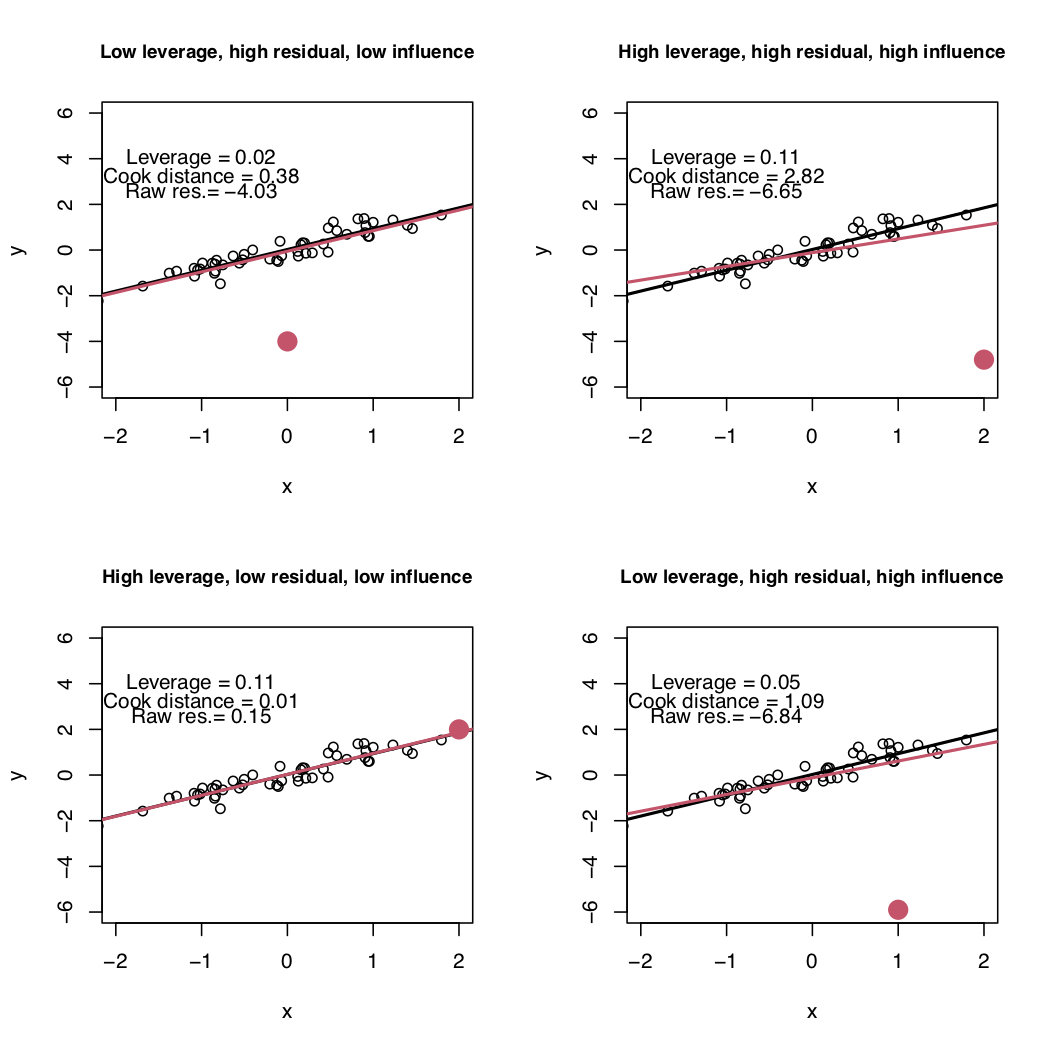
📌 이상치(Outlier) vs 레버리지(Leverage) vs 영향점(Influential Point)

이상치(Outlier)

전체적인 데이터 분포로부터 멀리 떨어져 있는 큰 잔차를 갖는 관측치

레버리지(Leverage)

독립변수 X가 전체적인 데이터의 독립변수 분포로부터 멀리 떨어져 있는 관측치

회귀계수에 큰 영향을 미치는 데이터

회귀선의 기울기 변화에 항상 크게 영향을 준다고 보기는 어려움

영향점(Influential Point)

회귀분석 결과 추정된 회귀선의 기울기를 크게 변화 시키는 관측치

💻 코드 예시

# 회귀분석 실시
import statsmodels.api as sm
import statsmodels.formula.api as smf

lm = smf.ols(formula='score ~ mid_exam + final_exam', data=df).fit()
print(lm.summary())

# result(Example)

                            OLS Regression Results                            
==============================================================================
Dep. Variable:                  score   R-squared:                       0.889
Model:                            OLS   Adj. R-squared:                  0.876
Method:                 Least Squares   F-statistic:                     68.23
Date:                Sun, 15 Oct 2023   Prob (F-statistic):           7.55e-09
Time:                        10:27:20   Log-Likelihood:                -57.541
No. Observations:                  20   AIC:                             121.1
Df Residuals:                      17   BIC:                             124.1
Df Model:                           2                                         
Covariance Type:            nonrobust                                         
==============================================================================
             coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
Intercept     16.9406      4.692      3.611      0.002       7.041      26.840
mid_exam       0.2750      0.055      4.959      0.000       0.158       0.392
final_exam     0.4957      0.053      9.371      0.000       0.384       0.607
==============================================================================
Omnibus:                        1.716   Durbin-Watson:                   1.959
Prob(Omnibus):                  0.424   Jarque-Bera (JB):                0.961
Skew:                           0.043   Prob(JB):                        0.618
Kurtosis:                       1.929   Cond. No.                         436.
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

📌 R-Squared vs Adjusted R-Squared

R-Squared (결정계수)

모형의 설명력을 의미

회귀식을 통해서 계산된 예측치가 실제 y값(종속변수)을 얼마나 잘 설명하는지를 의미

Adjusted R-Squared (수정된 결정계수)

다변량 회귀분석에선느 독립변수가 유의하든, 유의하지 않든 독립변수의 수가 많아지면 결정계수가 높아짐

이러한 결정계수의 단점을 보완하기 위해 독립변수의 개수를 고려해주는 수정된 결정계수가 필요

🔦잔차(residual)의 종류

✅ 레버리지 (Leverage)
👉 독립변수의 각 관측치가 독립변수들의 평균에서 떨어진 정도를 반영하는 통계량
👉 0과 1 사이의 값을 가지며, 일반적으로 레버리지 평균의 2~4배를 초과하는 관측치를 이상치로 간주

💻 코드 예시

leverage = infl.hat_matrix_diag
print('Leverage: \n', leverage)
print('Outliers using Leverage: \n', np.where(leverage > 3*np.mean(leverage)))

# result (Example)

Leverage: 
 [0.39638502 0.17369026 0.07289402 0.1191587  0.06309047 0.46679287
 0.06866284 0.05440394 0.05373713 0.05471108 0.06551602 0.07311863
 0.2782858  0.09527892 0.06827082 0.07438725 0.29825852 0.15865782
 0.11759661 0.24710329]
Outliers using Leverage: 
 (array([5], dtype=int64),)

✅ 표준화 잔차 (Standardized Residual)
👉 (잔차-잔차의 평균)/표준편차
👉 잔차를 평균 0, 표준편차 1(표준정규(Z)분포)으로 표준화 시킨 값
👉 일반적으로 표준화 잔차의 절대값이 2(2 표준편차) 또는 3(3 표준편차)을 초과하는 관측치를 이상치로 간주

💻 코드 예시

resid_standard = lm.resid_pearson
print('Standardized Residuals: \n', resid_standard)
print('Outliers using Standardized Residuals: \n', np.where(np.abs(resid_standard) > 2))

# result (Example)

Standardized Residuals: 
 [ 0.6218816  -0.13777096 -1.42333237 -0.72930398 -0.23743333  1.4516168
  0.42569816 -0.70488526 -0.63825154  0.27130668 -1.09327847  1.38521274
 -0.30553739 -1.55454376  0.37433833  0.67678102  1.11364219 -1.06337647
  0.11555116  1.45168485]
Outliers using Standardized Residuals: 
 (array([], dtype=int64),)

✅ 내적 스튜던트화 잔차(Internally Studentized Residual)

\boxed{r_{i}=\frac{e_{i}}{SE(e_{i})}=\frac{e_{i}}{s\sqrt{1-h_{ii}}}}

👉 각각의 잔차를 잔차의 표준오차(잔차의 표준편차의 추정치)로 나눈 통계량
👉 보통 $\plusmn$ 3(3 표준편차)을 초과하면 이상치로 간주

💻 코드 예시

resid_student = infl.resid_studentized_internal
print('Studentized Residuals: \n', resid_student)
print('Outliers using Studentized Residuals: \n', np.where(np.abs(resid_student) > 3))

# result (Example)

Studentized Residuals: 
 [ 0.80043801 -0.15156057 -1.47822871 -0.77706929 -0.24529735  1.98794339
  0.44111142 -0.72487914 -0.65612407  0.27904754 -1.13095381  1.43881316
 -0.35965138 -1.634352    0.3878104   0.70345044  1.32940438 -1.15931303
  0.12301008  1.67303352]
Outliers using Studentized Residuals: 
 (array([], dtype=int64),)

✅ 외적 스튜던트화 잔차(External Studentized (Deleted) Residual)

\boxed{r_{i}=\frac{y_{i}-\hat{y_{(i)}}}{SE(e_{i})}}

👉 해당 관측치를 제외하고 추정된 회귀모형으로부터 산출된 스튜던트 잔차
🧩 만일 i번째 자료를 제외한 다음에 회귀분석을 실시하고 i번째 자료를 예측했을 때 잔차가 적을 경우 해당 모형은 매우 좋은 모형!
👉 보통 $\plusmn$ 3(3 표준편차)을 초과하면 이상치로 간주

💻 코드 예시

resid_student_remove = infl.resid_studentized_external
print('Studentized Deleted Residuals: \n', resid_student_remove)
print('Outliers using Studentized Deleted Residuals: \n', np.where(np.abs(resid_student_remove) > 3))

# result (Example)

Studentized Deleted Residuals: 
 [ 0.79159921 -0.14713479 -1.53621904 -0.76762414 -0.23839565  2.20135802
  0.43041124 -0.71436276 -0.64474985  0.27133802 -1.14094722  1.4894885
 -0.35024811 -1.72702753  0.37790671  0.69260187  1.36247606 -1.17198052
  0.11939045  1.77584804]
Outliers using Studentized Deleted Residuals: 
 (array([], dtype=int64),)

✅ 쿡의 거리 (Cook’s Distance)

\boxed{D_{i}=\frac{\sum_{j=1}^{n} (\hat{y_{i}}-\hat{y_{i}})^2} {pMSE}  LOF_{k}(p) : 관측치 p의 이상치 정도}

👉 추정된 회귀모형에 대한 각 관측치들의 전반적인 영향력을 측정하기 위해 잔차와 레버리지를 동시에 고려한 척도
👉 회귀선의 모양에 크게 영향을 끼치는 점을 찾는 방법
👉 쿡의거리가 $D_{i} > \frac{4}{n-p-1}$ (일반적으로 1) 일 경우 이상치로 간주

💻 코드 예시

(cooks, p) = infl.cooks_distance
print('Cook\'s Distance: \n', cooks)
print('Outliers using Cook\'s Distance: \n', np.where(np.abs(cooks) > 1))

# result (Example)

Cook's Distance: 
 [1.40246289e-01 1.60947344e-03 5.72696470e-02 2.72286643e-02
 1.35061193e-03 1.15322762e+00 4.78178659e-03 1.00770787e-02
 8.14916906e-03 1.50226254e-03 2.98912530e-02 5.44366574e-02
 1.66252429e-02 9.37674451e-02 3.67335640e-03 1.32560738e-02
 2.50385209e-01 8.44829326e-02 6.72183422e-04 3.06218306e-01]
Outliers using Cook's Distance: 
 (array([5], dtype=int64),)

✅ DFFITS(Difference of Fits)
👉 모든 관측치를 활용하여 추정된 회귀모형 예측치와 해당 관측치를 제외한 후 추정된 회귀모형의 예측치 변화 정도를 측정하는 방법
👉 DFFITS 값이 클수록 이상치일 가능성이 높음

💻 코드 예시

(dffits, p) = infl.dffits_internal
print('DFFITS: \n', dffits)
print('Outliers using DFFITS: \n', np.where(dffits > 1))

# result (Example)

DFFITS: 
 [ 0.64864387 -0.06948684 -0.41449842 -0.28580761 -0.06365403  1.86002228
  0.11977212 -0.17387132 -0.15635699  0.06713261 -0.29945577  0.40411629
 -0.22332875 -0.53037943  0.10497652  0.19941971  0.86669235 -0.50343698
  0.04490602  0.95846488]
Outliers using DFFITS: 
 (array([5], dtype=int64),)

✅ DFBETAS(Difference of Betas)
👉 모든 관측치를 활용하여 추정된 회귀모형의 회귀계수와 해당 관측치를 제외한 후 추정된 회귀모형의 회귀계수 변화 정도를 측정하는 방법
👉 자료의 수가 적은 경우 DFBETAS 절댓값이 1, 자료의 수가 많은 경우 절댓값이 $2/\sqrt{n}$ 보다 크면 이상치로 간주

💻 코드 예시

dfbetas = infl.dfbetas
print('DFBETAS: \n', dfbetas)
print('Outliers using DFBETAS: \n', np.where(dfbetas.max(axis=1) > 1, ))

# result (Example)

DFBETAS: 
 [[ 0.63235178 -0.42212889 -0.3328359 ]
 [-0.05441214  0.05424166  0.00607284]
 [-0.31463228  0.15141531  0.15391987]
 [-0.19425993 -0.01463151  0.21318143]
 [-0.00934794 -0.02364202  0.01975385]
 [ 0.67458966  1.11482964 -1.78614232]
 [ 0.08156042 -0.03803302 -0.03902752]
 [-0.08150729  0.01687934  0.04143388]
 [ 0.00191513 -0.00764477 -0.03745664]
 [ 0.01277945  0.01556169 -0.01405732]
 [-0.03618125 -0.12733751  0.09747281]
 [-0.06890755 -0.04706725  0.23523728]
 [-0.04583282  0.16811238 -0.13423094]
 [ 0.26788527 -0.32434691 -0.14079065]
 [-0.03214709  0.03356423  0.03337099]
 [-0.02951452  0.11231916 -0.0271782 ]
 [ 0.05327063 -0.61165291  0.64324072]
 [ 0.34363815 -0.30564277 -0.22276607]
 [-0.02590088  0.02039566  0.02139251]
 [-0.7839719   0.58919933  0.55982065]]
Outliers using DFBETAS: 
 (array([5], dtype=int64),)

💡 처리 방법

✅ 포함 (Inclusion)
👉 데이터 세트에 이상치를 그대로 유지
👉 이상현상의 파악이 목적인 경우 주로 사용

✅ 수정 (Correction)
👉 이상치가 오류임이 판정될 경우 올바른 값으로 수정
👉 거의 발생하지 않음

✅ 제거 (Deletion)
👉 결측값으로 대체 후 결측값 처리
👉 데이터의 손실이 발생 → 자유도의 감소 → 통계적 검정력 저하
👉 표본의 수가 충분하고 결측값이 10-15% 이내일 때에는 결측값을 제거한 후 분석하여도 결과에 크게 영향을 주지 않음
👉 일반적인 추세를 구하는 것이 목적일 경우 사용

✅ 교체 (Replacement)
👉 표본 평균과 같은 대표값이나 극단값으로 교체
👉 대표값으로 교체할 경우 → 잔차 변동의 왜곡이 발생 → 잘못된 통계적 결론 유도
👉 모수 추정 시 편향(bias) 발생
👉 일반적으로 선호하는 방법

✅ 조정 (Accomodation)
👉 이상치는 그대로 유지하나 비모수 통계와 같이 이상치에 영향이 적은 방법을 적용

✅ 변환 (Transformation)
👉 이상값에 자연로그를 취해서 값을 감소시킴

✅ 데이터 분리 (Data Splitting)
👉 이상값이 많을 경우에 사용하는 방법으로 서로 다른 그룹으로 통계적인 분석을 실행하여 처리
👉 각각의 그룹에 대해서 통계적인 모형을 생성하고, 결과를 결합하는 방법을 사용함

🙏 Reference

https://gannigoing.medium.com/%EB%8D%B0%EC%9D%B4%ED%84%B0-%EC%9D%B4%EC%83%81%EC%B9%98-outlier-%EC%9D%98-%EA%B8%B0%EC%A4%80%EC%9D%80-%EB%AC%B4%EC%97%87%EC%9D%BC%EA%B9%8C-f11f60bf901a
https://luvris2.tistory.com/548
https://hongl.tistory.com/100
https://specialscene.tistory.com/63
https://blog.naver.com/lingua/221909198917
https://devhwi.tistory.com/16
https://repository.hira.or.kr/bitstream/2019.oak/2240/2/%EC%9D%B4%EC%83%81%EC%B9%98%20%ED%83%90%EC%83%89%EC%9D%84%20%EC%9C%84%ED%95%9C%20%ED%86%B5%EA%B3%84%EC%A0%81%20%EB%B0%A9%EB%B2%95.pdf

양승웅

이전 포스트

[PP] Anomaly Detection

다음 포스트

[PP] Data Cleansing(2)_이상치(Outliers)

PreProcessing

📢 개요

✏️ 이상치(Outlier)란?

❓ 발생 원인

1) 비자연적 이상치 (Non-Natural Outlier)

2) 자연적 이상치 (Natural Outlier)

🔎 탐색

1. 통계적 방법

1.1 Z-Score (표준화 점수)

1.2 Modified Z-Score

1.3 IQR (Interquantile Range / 사분위수 범위)

1.4 Grubb's t-test

1.5 Generalized ESD (Extreme Studentized Deviate) test

1.6 Chi-Square test (카이제곱 검정)

1.7 Dixon's Q-test

1.8 Mahalanobis Distance (마할라노비스 거리)

2. Model-based Method

2.1 LOF(Local Outlier Factor)

2.2 iForest(Isolation Forest)

2.3 DBSCAN(Density Based Spatial Clustering of Applications with Noise)

2.4 회귀진단 (Regression Diagnostics)

🔦잔차(residual)의 종류

💡 처리 방법

🙏 Reference

[PP] Anomaly Detection

[PP] Data Profiling(데이터 프로파일링)

0개의 댓글