함수의 정의
- 대수학에서 이미 익숙하다시피, x∈R인 각각의 수 x를 y∈R인 특정한 값 y=f(x)로 할당하는 함수 f로 이해할 수 있다.
- 단, 함수의 개념은 실수 집합뿐만 아니라 임의의 집합들을 대상으로 일반화시킬 수 있음.
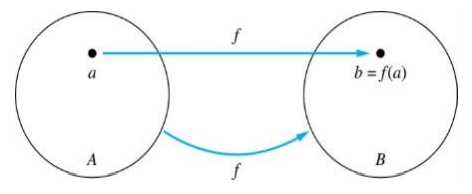
- 정의: A와 B를 집합이라 하자. 임의의 집합 A, B에 대해 f:A→B(A에서 B로 사상시키는)인 함수 f는 x∈A인 각각의 원소 x를 f(x)∈B인 반드시 하나의 원소 f(x)로의 특정한 할당으로 볼 수 있다.
- 만약 b가 A의 요소인 a에 대한 함수 f에 의해 할당되는 B의 unique element라면, f(a) = b라고 쓴다.
- 함수는 사상(mappings) 또는 변환(transformations) 라고도 불린다.
- 함수 f는 A의 원소 각각에 대해서 B의 원소를 단 하나만 대응시킴
함수의 그래픽적인 표현
- 함수는 그래픽적으로도 표현될 수 있다:
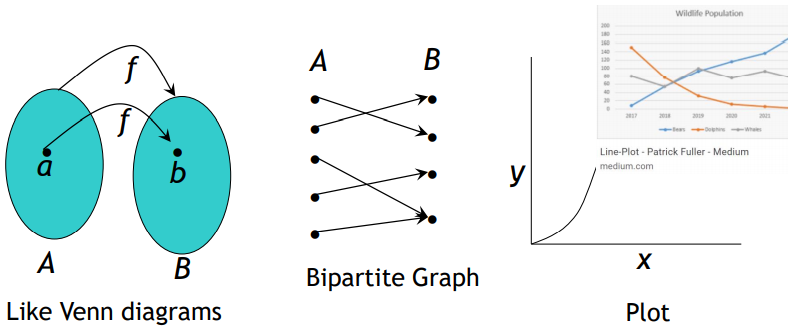
함수의 예
- 명제함수(proposition)은 situations으로부터 진리값 {T,F}로의 함수로 볼 수 있다.
- situation theory로 불리는 logic sysem.
- p="비가온다."; s=지금 우리의 상황, p(s)∈{T,F}
- 명제 연산자(propositional operator)는 진리값의 ordered pairs로부터 진리값으로의 함수로 볼 수 있다.
- ∨((F,T)) = T
- →((T,F)) = F
- 집합 연산자(set operator) (∩, ∪ ⋯)는 집합의 pair로부터 집합으로의 함수로 볼 수 있다.
- Example: ∩({1,3},{3,4}) = {3}
함수 용어(Function's Terminology)
- 만약 f:A→B, f(a)=b (단, a∈A & b∈B)라면, then:
- A는 f의 정의역(domain)이다.
- B는 f의 공역(codomain)이다.
- b는 f에 의한 a의 상(image)이다.
- a는 f에 의한 b의 원상(pre-image)이다.
- 일반적으로 b는 1개보다 많은 원상을 갖고있다.
- f의 치역(range) R⊆B는 {b | ∃a f(a)=b}이다.
치역(range) vs 공역(codomain)
- 함수의 치역은 전체 공역이 아닐 수 있다.
- 치역은 공역의 부분 집합(particular set)으로서, 함수에 의해 실제 매핑이 일어난 원소의 집합임
- example:
- 가정 - 함수 f는 학생을 성적{A, B, C, D, F}로 매핑시키는 함수
- 성적을 부여하기 전에는 공역은 {A, B, C, D, F}로 알 수 있으나, 그 치역은 알지 못함!
- 가정 - 모두 A등급과 B등급을 부여하였음.
- 그러면 치역은 {A, B}로 결정되었지만, 공역은 그대로 {A, B, C, D, F}임
함수 연산자
- +, x ("plus", "times")는 실수 R에 대한 이항 연산자(binary operators)임.
- 만약 f, g: R→R라면, 함수연산자의 정의는:
- (f + g):R→R, where (f + g)(x) = f(x) + g(x)
- (f x g): R→R, where (f x g)(x) = f(x) x g(x)
- example:
함수에서 집합의 상
- f:A→B, S⊆A가 주어졌을 때,
- S의 상(image)은 S의 모든 원소의 상으로 구성된 B의 부분집합
- f(S) = {f(s) | s∈S} = {b | ∃s∈S(f(s)=b)}
- f의 치역은 f의 정의역에 대한 상으로 정의할 수 있음
- example:
- A = {a, b, c, d, e}, B = {1, 2, 3, 4}, S = {b, c, d}
- f(a) = 2, f(b) = 1, f(c) = 4, f(d) = 1, f(e) = 1
- f(S) = {1, 4}
일대일 함수(=one-to-one, injective)
- 일대일 함수(=one-to-one, injective) : 치역의 모든 원소는 오직 하나의 원상(pre-image)를 가짐
- 형식적인 표현: f:A→B가 주어졌을 때 "x는 injective"라는 말은 (¬∃x,y: x≠y ∧ f(x)=f(y)) 이다.
- 정의역의 하나의 원소는 치역의 하나의 원소로 대응
- 즉, 정의역과 치역은 같은 카디널리티를 가진다. (공역은 더 크거나 같다.)
∀a∀b(a≠b → f(a) ≠ f(b)) 혹은 ∀a∀b(f(a) = f(b) → a=b) 로도 나타낼 수도 있다.
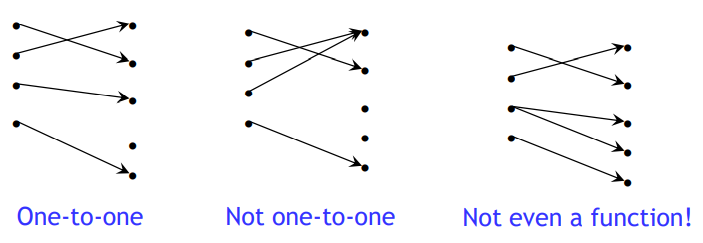
일대일 함수의 충분조건
- 단조증가함수(strictly or monotonically increasing function) : 모든 x,y에 대해 x<y → f(x)<f(y)
- 단조감소함수(strictly or monotonically decreasing function) : 모든 x,y에 대해 x<y → f(x)>f(y)
- f가 단조증가(or 감소)함수라면, f는 일대일 함수(one-to-one)이다. e.g,
- 역(converse)은 성립할 수도 있고 그렇지 않을 수도 있다.e.g,
전사함수(=onto)
- 전사 함수(=onto, surjective) : 치역과 공역이 동일
- 형식적 표현: (∀b∈B, ∃a∈A: f(a)=b)


