deep.daiv 동아리에서 진행했으며 팀원과 함께 정리한 내용입니다.
Lecture 2
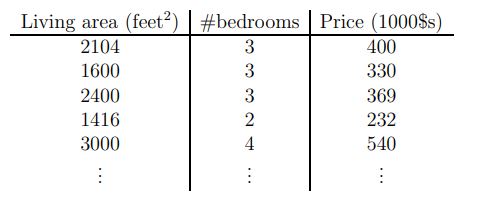
Part.1 Linear regression(선형 회귀)
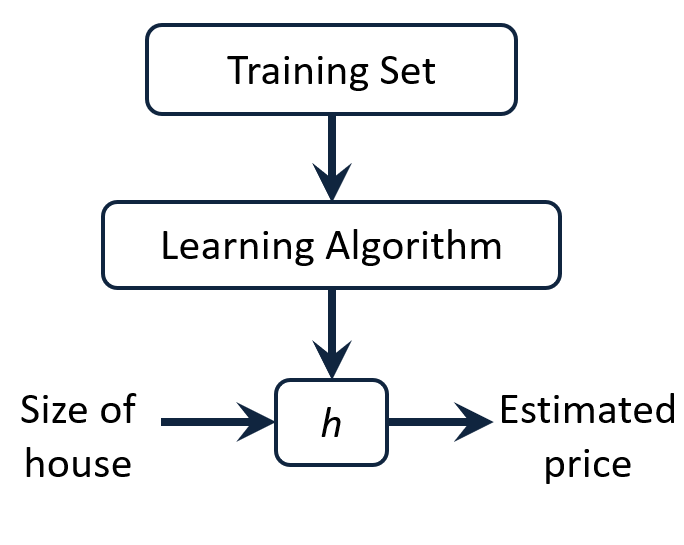
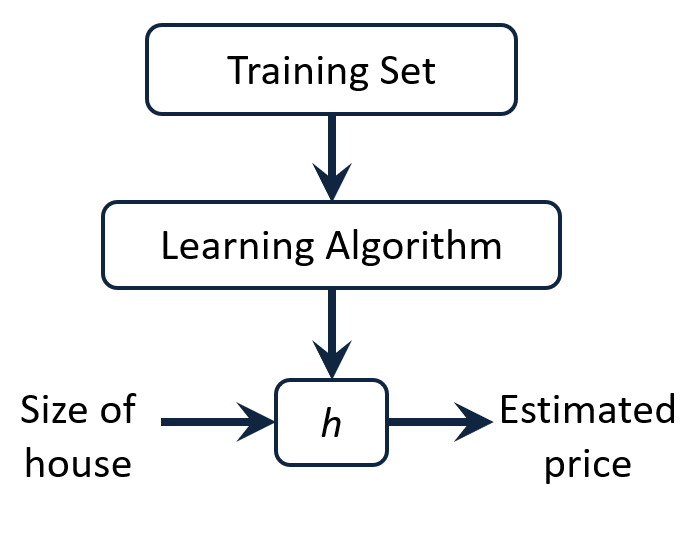
Process of supervised learning: feed training set to a learning algorithm, and make prediction about housing prices
💡 $h$(hypothesis)란, input과 output의 관계를 나타내는 함수이다.
size of house 라는 입력값이 h h h h h h
∗ ∗ h **h ∗ ∗ h
h ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 , h ( x ) = ∑ j = 0 j = n θ j x j , x 0 = 1 θ = [ θ 0 θ 1 θ 2 ] x = [ x 0 x 1 x 2 ] , θ j x j = θ T x = [ θ 0 θ 1 θ 2 ] × [ x 0 x 1 x 2 ] h(x)=\theta _0+\theta_1x_1+\theta_2x_2 , \\h(x)=\sum_{j=0}^{j=n} \theta_j x_j , x_0=1 \\ \theta= \begin{bmatrix}\theta_0 \\ \theta_1 \\ \theta_2 \end{bmatrix} x= \begin{bmatrix}x_0 \\ x_1 \\ x_2 \end{bmatrix} , \theta_jx_j=\theta^Tx= \begin{bmatrix}\theta_0 &\theta_1 & \theta_2 \end{bmatrix} \times \begin{bmatrix}x_0 \\ x_1 \\ x_2 \end{bmatrix} h ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 , h ( x ) = j = 0 ∑ j = n θ j x j , x 0 = 1 θ = ⎣ ⎢ ⎡ θ 0 θ 1 θ 2 ⎦ ⎥ ⎤ x = ⎣ ⎢ ⎡ x 0 x 1 x 2 ⎦ ⎥ ⎤ , θ j x j = θ T x = [ θ 0 θ 1 θ 2 ] × ⎣ ⎢ ⎡ x 0 x 1 x 2 ⎦ ⎥ ⎤
💡 $\theta_j$: 가중치(parameter or weights)라고 불리는데 , $\theta_j$를 조정하여 주어진 데이터에 가장 잘 맞는 직선을 찾아갈 수 있다.
n n n
hypothesis 함수의 정확도를 측정하기 위해 cost function(비용함수)가 필요하다.
c o s t f u n c t i o n = J ( θ ) = 1 2 ∑ i = 1 m ( h θ ( x i ) − y i ) 2 cost function=J(\theta) = \frac{1}{2}\sum_{i=1}^{ m } {(h_\theta(x^i) - y^i)^2} c o s t f u n c t i o n = J ( θ ) = 2 1 i = 1 ∑ m ( h θ ( x i ) − y i ) 2
💡 $m$ : 트레이닝 샘플의 개수이다.
Batch Gradient descent(경사하강법)
경사 하강법은 앞서 설명한 cost function 을 최소로 만드는 적당한 parameter θ \theta θ
θ j : = θ j − 1 2 α ∑ i = 1 m ( h ( x i ) − y i ) x j i ( for j=0,1,2... n ) = θ j − ∂ ∂ θ j J ( θ ) \theta_j := \theta_j - \frac{1}{2}\alpha\sum_{i=1}^{ m } {(h(x^i) - y^i)}x_j^i \\ \text{( for j=0,1,2... n )}=\theta_j-\frac\partial{\partial\theta_j}J(\theta) θ j : = θ j − 2 1 α i = 1 ∑ m ( h ( x i ) − y i ) x j i ( for j=0,1,2... n ) = θ j − ∂ θ j ∂ J ( θ )
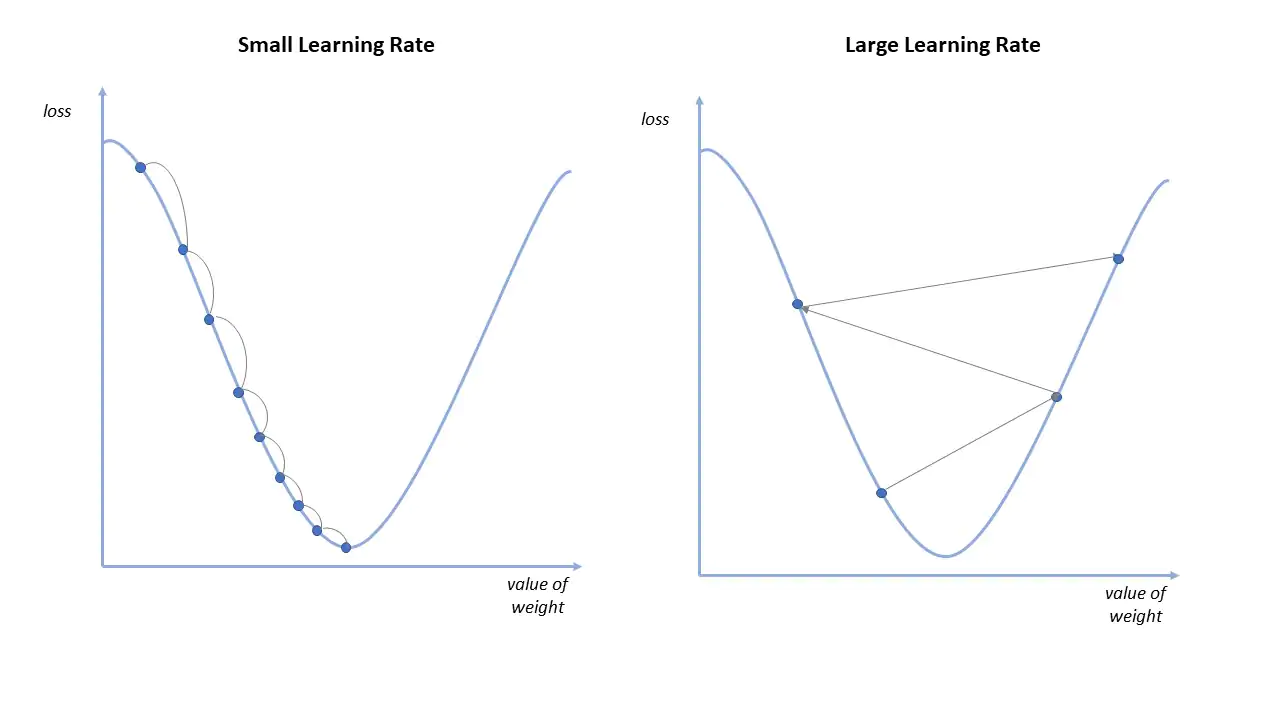
💡 $\alpha$ : learning rate
$:=$ : 새로운 $\theta$ 값의 항을 왼쪽에, 이전의 $\theta$에 어떤한 변화를 주는 항을 오른쪽에 두는 기호이다.
start with some θ \theta θ θ = 0 ⃗ \theta = \vec{0} θ = 0
Keep changing θ \theta θ J ( θ ) J(\theta) J ( θ )
Repeat until convergence
More details about θ j \theta_j θ j
θ j : = θ j − α ∂ ∂ θ j J ( θ ) ( f o r j = 0 , 1 , 2 ) \theta_j := \theta_j - \alpha \frac\partial{\partial\theta_j}J(\theta)\space\space (for\space j = 0,1,2) θ j : = θ j − α ∂ θ j ∂ J ( θ ) ( f o r j = 0 , 1 , 2 )
∂ ∂ θ j J ( θ ) = ∂ ∂ θ j ( h θ ( x ) − y ) 2 = 2 × 1 2 ( h θ ( x ) − y ) ∂ ∂ θ j ( h θ ( x ) − y ) ( b y c h a i n r u l e ) = ( h θ ( x ) − y ) ∂ ∂ θ j ( θ 0 x 0 + θ 1 x 1 + . . . + θ n x n − y ) = ( h θ ( x ) − y ) x j \space \frac\partial{\partial\theta_j} J \left(\theta\right) \\ = \frac\partial{\partial\theta_j}{(h_\theta(x) - y)^2} \\ = 2 \times \frac{1}{2}(h_\theta(x) - y) \frac\partial{\partial\theta_j}(h_\theta(x) - y) \space (by\space chain\space rule) \\ = (h_\theta(x) - y)\frac\partial{\partial\theta_j}(\theta_0x_0+\theta_1x_1 + ...+ \theta_nx_n - y) \\ = (h_\theta(x) - y)x_j ∂ θ j ∂ J ( θ ) = ∂ θ j ∂ ( h θ ( x ) − y ) 2 = 2 × 2 1 ( h θ ( x ) − y ) ∂ θ j ∂ ( h θ ( x ) − y ) ( b y c h a i n r u l e ) = ( h θ ( x ) − y ) ∂ θ j ∂ ( θ 0 x 0 + θ 1 x 1 + . . . + θ n x n − y ) = ( h θ ( x ) − y ) x j
θ j : = θ j − α ( h θ ( x ) − y ) x j \theta_j := \theta_j - \alpha (h_\theta(x) - y)x_j θ j : = θ j − α ( h θ ( x ) − y ) x j
We have i t h i^{th} i t h θ j : = θ j − α ∑ i = 1 m ( h ( x i ) − y i ) x j i \theta_j := \theta_j - \alpha\sum_{i=1}^{ m } {(h(x^i) - y^i)}x_j^i θ j : = θ j − α ∑ i = 1 m ( h ( x i ) − y i ) x j i
💡 편미분항을 빼주는 이유는 기울기가 양수이면 왼쪽으로 움직이고,반대로 음수이면 오른쪽으로 움직여야 local optima로 가까워지기 때문이다.
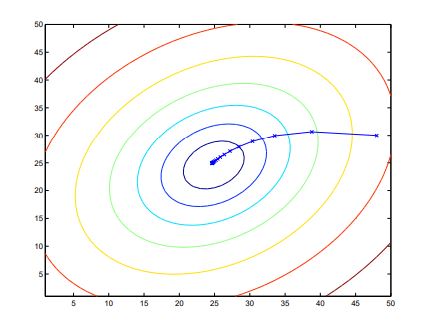
이러한 과정들을 마치게 되면 θ \theta θ h h h
θ \theta θ J ( θ ) J(\theta) J ( θ )
l e a r n i n g r a t e learning\space rate l e a r n i n g r a t e α \alpha α θ j \theta_j θ j Batch Gradient Descent 하나의 파라미터를 업데이트 하기위해서 ∑ i = 1 m ( h ( x i ) − y i ) x j i \sum_{i=1}^{m} {(h(x^i) - y^i)}x_j^i ∑ i = 1 m ( h ( x i ) − y i ) x j i
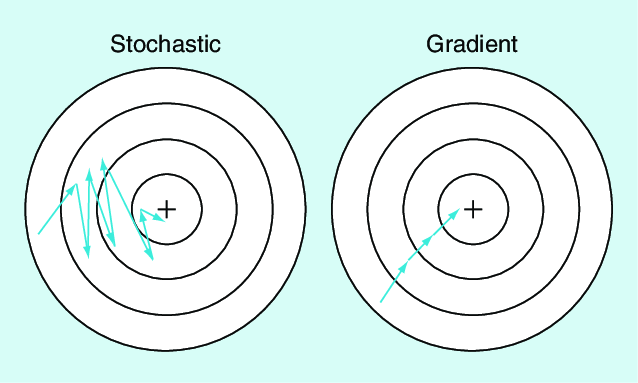
Stochastic Gradient Descent(확률적 경사하강법)
Batch Gradient Descent의 느린 속도의 단점을 보완하기 위해 Stochastic Gradient Descent를 사용한다.
R e p e a t f o r i = 1 t o m θ j : = θ j − α ( h ( x ( i ) ) − y ( i ) ) x j ( i ) Repeat \\ \quad for\space i = 1\space to \space m \\ \qquad \theta_j := \theta_j - \alpha {(h(x^{(i)}) - y^{(i)})}x_j^{(i)} R e p e a t f o r i = 1 t o m θ j : = θ j − α ( h ( x ( i ) ) − y ( i ) ) x j ( i )
SGD의 움직임을 보면, BGD보다 역동적으로 움직인다. 하지만, Global Minimum에 가깝게 움직이고 대신 수렴하지는 않는다. 이러한 특성 덕분에, BGD의 경우 local optima가 되면 더 이상 업데이트 하지 않지만, SGD는 local optima가 되더라도 global minimum을 찾을 가능성을 준다.
SGD를 사용하게 되면 global minimum에 근접한 값을 얻을 수 있지만, 최적의 값은 아니다. 이를 보완할 방법 중 하나는, learning rate를 시간이 지남에 따라 감소시키는 것이다. 변수의 움직임이 점점 더 작은 폭으로 움직이게 되어 global minimum에 가까운 값을 찾을 수 있다.
Normal equation(정규 방정식)
정규 방정식을 통해 θ \theta θ
BGD 방식과는 다르게 learning rate 가 필요하지 않다
정규방정식을 사용하면 반복적인 알고리즘의 구현 없이 한번에 θ \theta θ
n이 많아질수록 계산은 거의 불가능하다.
d e f i n e ∇ θ J ( θ ) = d e r i v a t i v e o f J ( θ ) r e s p e c t t o θ ∈ R n + 1 define\space \nabla_\theta J(\theta) = derivative\space of\space J(\theta) \space respect\space to\space \theta \in \mathbb{R}^{n+1} d e f i n e ∇ θ J ( θ ) = d e r i v a t i v e o f J ( θ ) r e s p e c t t o θ ∈ R n + 1 ∇ θ J ( θ ) = [ ∂ J ∂ θ 0 ∂ J ∂ θ 1 ∂ J ∂ θ 2 ] \nabla_\theta J(\theta) = \begin{bmatrix} \frac{\partial J}{\partial\theta_0} \\ \frac{\partial J}{\partial\theta_1} \\ \frac{\partial J}{\partial\theta_2}\end{bmatrix} ∇ θ J ( θ ) = ⎣ ⎢ ⎡ ∂ θ 0 ∂ J ∂ θ 1 ∂ J ∂ θ 2 ∂ J ⎦ ⎥ ⎤
Example S u p p o s e A = ( A 11 A 12 A 21 A 22 ) i s a 2 b y 2 m a t r i x Suppose\space A = \begin{pmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{pmatrix}\space is\space a \space 2\space by\space 2\space matrix S u p p o s e A = ( A 1 1 A 2 1 A 1 2 A 2 2 ) i s a 2 b y 2 m a t r i x T h e f u n c t i o n f : R 2 × 2 ↦ R i s g i v e n f ( A ) = A 11 + A 12 2 The\space function\space f:\mathbb{R}^{2\times2} \mapsto \mathbb{R}\space is\space given\space f(A) = A_{11} +A_{12}^2 T h e f u n c t i o n f : R 2 × 2 ↦ R i s g i v e n f ( A ) = A 1 1 + A 1 2 2 ∇ A f ( A ) = ( ∂ f ∂ A 11 ∂ f ∂ A 12 ∂ f ∂ A 21 ∂ f ∂ A 22 ) = ( 1 2 A 12 0 0 ) \nabla_A f(A) = \begin{pmatrix} \frac{\partial f}{\partial A_{11}} & \frac{\partial f}{\partial A_{12}} \\ \frac{\partial f}{\partial A_{21}} & \frac{\partial f}{\partial A_{22}} \end{pmatrix} = \begin{pmatrix} 1 & 2A_{12} \\ 0 & 0 \end{pmatrix} ∇ A f ( A ) = ( ∂ A 1 1 ∂ f ∂ A 2 1 ∂ f ∂ A 1 2 ∂ f ∂ A 2 2 ∂ f ) = ( 1 0 2 A 1 2 0 )
J ( θ ) J(\theta) J ( θ ) J ( θ ) J(\theta) J ( θ ) θ \theta θ
What is tr A or ‘trace of A ? n by n 행렬 A에 대해서, 모든 대각항들의 합으로 정의한다 :t r A = ∑ i = 1 n A i i tr A = \sum_{i=1}^{n} A_{ii} t r A = i = 1 ∑ n A i i
t r A B = t r B A tr AB = tr BA t r A B = t r B A
t r A B C = t r C A B = t r B C A tr ABC = tr CAB = tr BCA t r A B C = t r C A B = t r B C A
또한, 두 행렬 A,B가 정사각행렬이면 다음을 만족한다.
t r A = t r A T tr A = tr A^{T} t r A = t r A T
t r ( A + B ) = t r A + t r B tr (A+B)=trA +trB t r ( A + B ) = t r A + t r B
t r a A = a t r A tr\space aA = a\space trA t r a A = a t r A
행렬 도함수에 관한 다음 4가지 식을 얻어 낼 수 있다.
∇ A t r A B = B T \nabla_A trAB = B^{T} ∇ A t r A B = B T ∇ A T f ( A ) = ( ∇ A f ( A ) ) T \nabla_{A^{T}}f(A) = (\nabla_Af(A))^{T} ∇ A T f ( A ) = ( ∇ A f ( A ) ) T ∇ A t r A B A T C = C A B + C T A B T \nabla_AtrABA^{T}C = CAB + C^{T}AB^{T} ∇ A t r A B A T C = C A B + C T A B T ∇ A det A = det A ( A − 1 ) T ( O n l y f o r n o n s i n g l u a r s q u a r e m a t r i x ) \nabla_A \det A = \det A (A^{-1})^{T} \space (Only\space for\space non\space singluar\space square\space matrix) ∇ A det A = det A ( A − 1 ) T ( O n l y f o r n o n s i n g l u a r s q u a r e m a t r i x )
( X θ − y ) = [ ( h ( x ( 1 ) ) − y ( 1 ) ) ( h ( x ( 2 ) ) − y ( 2 ) ) . . . . ( h ( x ( n ) ) − y ( n ) ) ] (X\theta - y) = \begin{bmatrix} {(h(x^{(1)}) - y^{(1)})} \\ {(h(x^{(2)}) - y^{(2)})} \\ . \\ .\\. \\. {(h(x^{(n)}) - y^{(n)})} \end{bmatrix} ( X θ − y ) = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ ( h ( x ( 1 ) ) − y ( 1 ) ) ( h ( x ( 2 ) ) − y ( 2 ) ) . . . . ( h ( x ( n ) ) − y ( n ) ) ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ Z T Z = ∑ Z 2 , J ( θ ) = 1 2 ( X θ − y ) T ( X θ − y ) Z^{T}Z = \sum Z^2, \space J(\theta) = \frac{1}{2}(X\theta - y)^{T}(X\theta-y) Z T Z = ∑ Z 2 , J ( θ ) = 2 1 ( X θ − y ) T ( X θ − y )
How to calculate ∇ θ J ( θ ) \nabla_\theta J(\theta) ∇ θ J ( θ ) ∇ θ J ( θ ) = ∇ θ 1 2 ( X θ − y ) T ( X θ − y ) \nabla_\theta J(\theta) = \nabla_\theta \frac{1}{2}(X\theta - y)^{T}(X\theta-y) ∇ θ J ( θ ) = ∇ θ 2 1 ( X θ − y ) T ( X θ − y ) = ∇ θ 1 2 [ θ T X T X θ − θ T X T y − y T X θ + y y T ] =\nabla_\theta \frac{1}{2}[ \theta^{T}X^{T}X\theta-\theta^{T}X^Ty-y^TX\theta+yy^T] = ∇ θ 2 1 [ θ T X T X θ − θ T X T y − y T X θ + y y T ] = 1 2 [ X T X θ + X T X θ − X T y − X T y ] = \frac{1}{2} [X^TX\theta + X^TX\theta - X^Ty - X^Ty] = 2 1 [ X T X θ + X T X θ − X T y − X T y ] = X T X θ − X T y = s e t 0 ⃗ = X^TX\theta - X^Ty \overset{set}{=} \vec{0} = X T X θ − X T y = s e t 0
X T X θ = X T y X^TX\theta = X^Ty X T X θ = X T y 마지막 식에서 θ \theta θ J ( θ ) J(\theta) J ( θ )
X의 가역행렬이 존재하지 않다면, 이는 중복되는 feature가 존재함을 의미한다. 따라서, 실제로 어떤 feature가 반복되는지 확인해야 한다.